指数SVD和Kriging模型的声波传感器三维温度场重建研究

辽宁工业大学机械工程与自动化学院，辽宁锦州 121001

一、引言

目前在储粮测温、炉膛测温通常采用声学法测温方法，但是由于在大部分温度场中布置传感器存在边界位置以及数目有限的问题，导致的弊端是测温点密度低，边界温度值无法得出。如果热点不是恰好出现在内部一定范围中，霉变、虫害通常就会蔓延到较大区域才能被发现，而控制处理措施不及时将导致储粮损失增大。

王明吉等[1]以最小二乘方法构建了三维温度场声学测量重建算法，对球对称型模型温度场进行了仿真重建；白燕[2]基于最小二乘法与傅里叶正则化方法进行了重建仿真，研究结果表明，当传感器数量增多时，其重建精度较高；王交峰等人[3]用最小二乘方法对航空发动机燃烧室环形出口温度场进行了重建。这些研究所提算法都要求被测区域划分的单元数小于系统所获得的投影数据数，因此原始重建出的温度点非常少，所带来的信息缺失无法通过插值运算弥补。

颜华等[4]在测量声波飞行时间时，将采样信号的互相关函数在峰值附近做三次样条插值，该方法对提高声学法温度场检测精度具有实际意义。后来，颜华又提出了一种径向基函数逼近和正则化的温度场重建算法[5,6]，结果表明此算法热点定位精度高，重建算法误差较小；

郑永骏[7]运用对偶Kriging模型插值分析气象资料，拟合4类半变异函数模型对降水分析精度较高；曾怀恩等[8]提出了Kriging方法运用在空间数据插值中，通过实例与反距离加权法相比较，证实了Kriging插值的优越性；王婧雅等[9]运用改进的克里金插值法对大尺度农田土壤墒情分布进行了插值，结果表明，模拟值与实测值具有较好的吻合度，两者的相对误差和相关系数均接近最优值，验证了修正克里金插值法具有可行性和可靠性。综上，Kriging模型虽应用广泛，但还没有应用到温度场重建的内外推中。

本文基于现有重建算法弊端及不足，提出了一种基于指数奇异值分解（(Singular Value Decomposition，SVD）的三维温度场重建算法，并将Kriging模型引入到温度场重建的内外推中，以正方体温度场空间为例，采用典型单峰、双峰、四峰模型温度场进行了重建及插值研究。结果表明，指数SVD算法和Kriging模型结合的重建温度场达到较高的精度指标。

二、温度场重建

声学法测温的主要过程，首先是在被测区域周围尽可能均匀的设置声波收发器，任意一个声波收发器发射信号，所有声波收发器接收信号，这样就形成穿过该被测区域的多条均匀分布的声波飞行路径，测量这些穿过被测区域的声波飞行时间；然后再利用合适的温度场重建算法和声速与温度的关系，重建出被测区域的温度场分布[10]。

气体介质中的声速、气体介质的绝对温度和气体介质的声音常数之间的关系为[1,6]：

其中，c—体介质中的声速，单位：m/s；

T—气体介质的绝对温度，单位：K；B—声音常数，由气体组成成分决定的。

在气体组成成分一定的条件下，B是一个常量，如被测气体为烟道混合气体时，B取19.08，被测气体为空气时，B取20.05[11]。

三、指数SVD和Kriging模型算法

1、指数SVD算法

假设被测空间温度场为T(x,y,z)，声速的倒数为f(x,y,z)，由公式（1）可得：

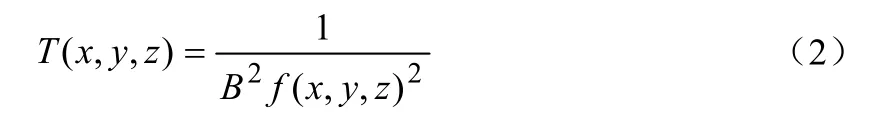
任一声波路径pk上，声波的飞行时间gk可以表示为：

其中，k—穿过三维温度场的有效声波飞行时间总数。

将被测空间划分成M个立方体网格，设第m个网格中心点坐标表示为(xm,ym,zm)，m∈[1,M]。

将f(x,y,z)离散为M个基函数的线性组合：

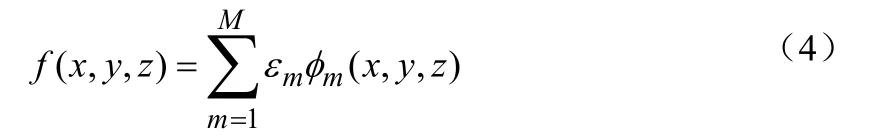
其中，εm—待定系数；

φm(x,y,z)—径向基函数[12]，有：

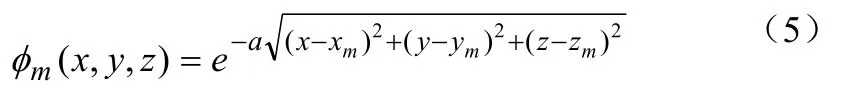
其中，a—径向基函数的形状参数，被测空间的大小和声波收发器的位置都影响形状参数的选取。

为了求解式公式（4）中的待定系数εm，合并式（3）、（4）和（5）得到：

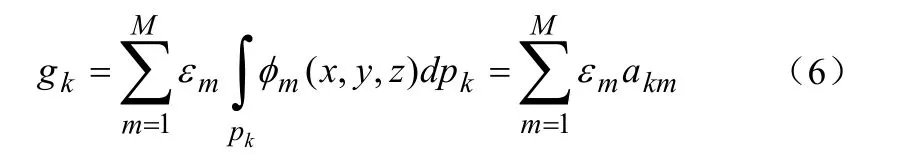
定义：A=(akm)k=1,…,K;m=a,…M；

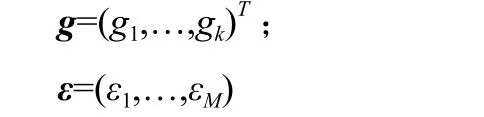
则公式（6）可写成：

对重建矩阵A作SVD分解：

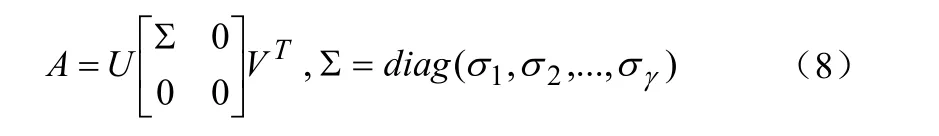
其中，σ1,σ2,…,σγ—重建矩阵A的γ个非零奇异值，σ1≥σ2≥ … ≥σγ≥ 0；

γ—重建矩阵A的秩；

U—列向量，正交矩阵AAT的特征向量；V—列向量，正交矩阵ATA的特征向量。

由此，可以推出A的伪逆为：

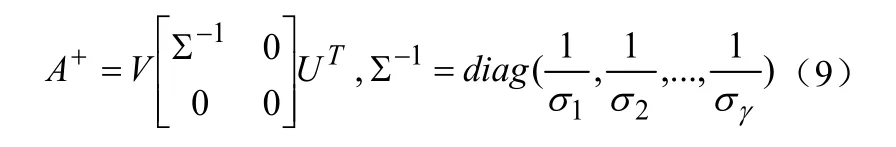
通过奇异值分解，式（7）可以写成

为了增加系统的抗噪声能力，用一个滤波函数对ε进行滤波：

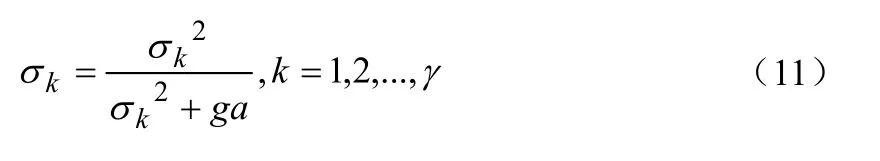
其中，g、a—滤波参数。

由此，通过合并（3）式（11）式，可以求的被测区域的声波传播速度，进而代入式（2）就可以求出M个空间网格的中心点温度值。

2、Kriging模型插值算法

Kriging模型[12]是一种基于统计理论的插值技术。通常Kriging模型变量x=[x1,...,xw]与真实响应y间的关系可表示为：

式中，f(x) —回归函数（一般采用多项式形式）；

λ—回归系数；

μ(x) —均值为0、方差为σ2的随机函数，μ(x)的协方差矩阵为：

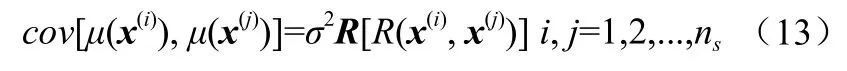
式中，ns—采样点数；

R—沿对角线对称的相关矩阵；

R(x(i),x(j)) —采样点x(i)与x(j)的相关函数，相关函数常用平稳高斯函数来表述：

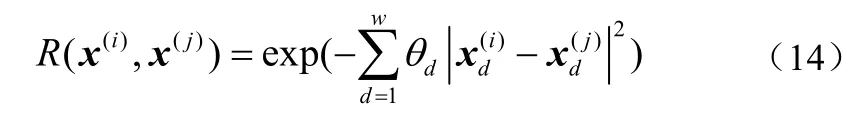
其中，θ=(θ1,θ2,…,θw)T—相关函数参数；

w—变量的维数。

位置x处的响应值y(x)的预测估计值为：

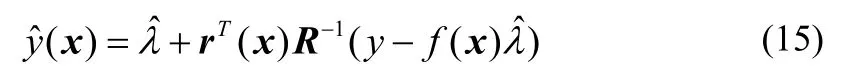
其中，λ的估计值；

y的长度为ns，包含样本数据的响应值；

rT(x)的长度为ns，是位置x和样本数据(x(1),)间的相关向量：

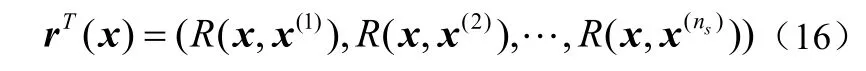
设λ的最优估计值为λ*，全局模型的方差估计值由λ*和y给出：

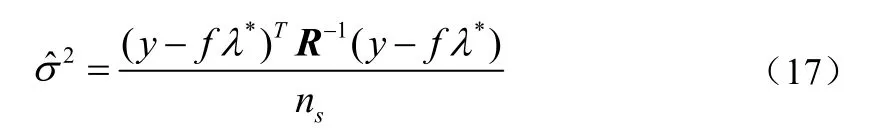
相关函数参数θ由极大似然估计给出，即在θd＞0时使下式最大：

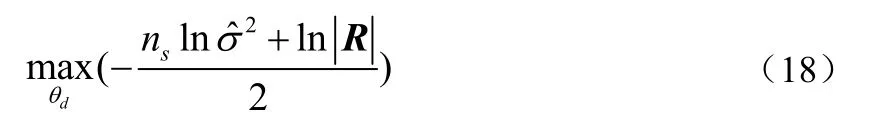
四、实验结果

本文利用声学法进行温度场的重建，将重建温度点进行内外推的插值，使得整个被测区域的三维温度场得到更加细化和边缘部分无遗漏的重建推算。

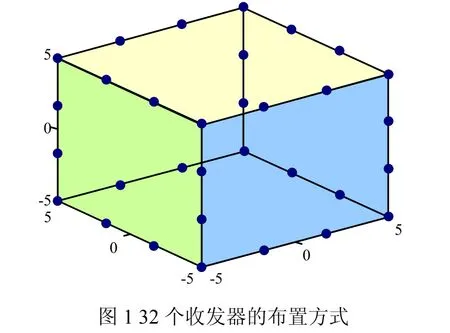
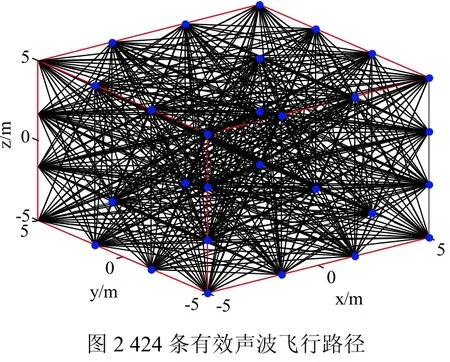
被测的三维空间为10m × 10m × 10m的正方体，如图1所示，在每个顶点及每条棱边三等分的间隔位置都放置一个声波发生器和一个声波接收器，这样在被测正方体的周围共放置32组声波收发器。飞行有效路径按照剔除棱边的选取方式，可以得到424条有效声波路径（如图2所示），计算有效声波路径上的声波飞行时间。将被测空间划分为1000个均匀的网格，计算重建矩阵。利用指数SVD法，重建出1000个网格的中心点温度值。

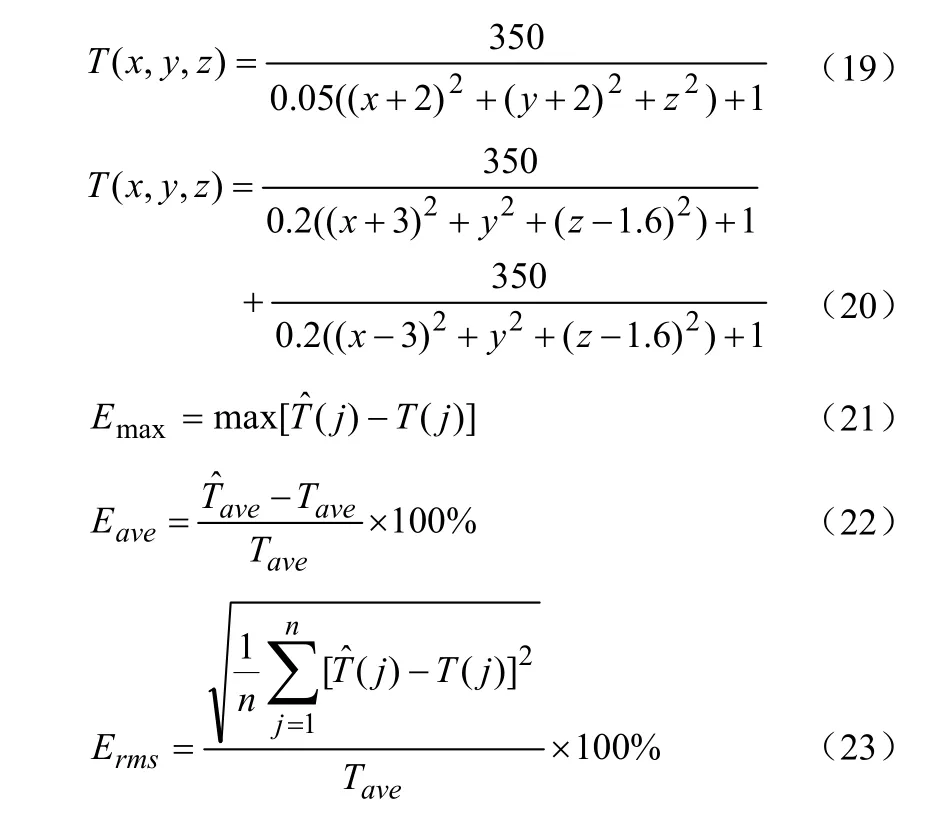
式中，n—被测区域所划分的网格（像素）的总数；

T(j)和—模型温度场和重建温度场第j个网格中心点的温度；

Tave和—模型温度场和重建温度场的平均温度。

表1为4种典型温度场重建后的最大相对误差、平均相对误差和均方根误差。双峰模型的重建温度场与模型温度场的三维展示图如图3所示。

根据表1与图3可知，通过指数SVD算法对4种温度场重建出的1000个网格的中心点温度值与模型中1000个相应位置真实值的三种误差结果比较小。但是被测温度场10m × 10m × 10m的范围内，所有边缘部分的剖分网格外部一半没有重建出来，内部的温度值也不够细化分布。

本文运用Kriging模型进行拟合插值，对以上指数SVD算法重建后待解决的填充与细致化问题进行研究。对重建出来的范围内的温度值进行内插与外推，剖分网格由原来的10 × 10 × 10个（即1000个）变为41 × 41 × 41个（即68921个）。

表2为4种典型温度场Kriging模型插值后的最大相对误差、平均相对误差和均方根误差。图4所示为经过Kriging模型插值后的双峰模型的重建温度场与模型温度场的三维展示图。

由表2和图4可知，指数SVD算法和Kriging拟合插值后对4种温度场重建出的41 × 41 × 41个（即68921个）网格的中心点温度值与模型中41 × 41 ×41个（即68921个）相应位置真实值的三种误差结果比较小。被测温度场10m × 10m × 10m的范围内的所有温度值能够较精确的重建出来，并得到了细致化展示。

五、结论

本文提出了指数SVD法与Kriging模型相结合的三维温度场重建方法。采用指数SVD法对典型单峰、双峰、四峰模型温度场进行了重建，kriging模型对重建温度场进行了内插、外推。研究表明：采用指数SVD和Kriging法对典型单峰、双峰、四峰模型温度场重建，重建最大温度相对误差小于2.2%、平均温度相对误差小于0.2%、温度均方根误差小于2%，适用模型广泛，且重建精度高。

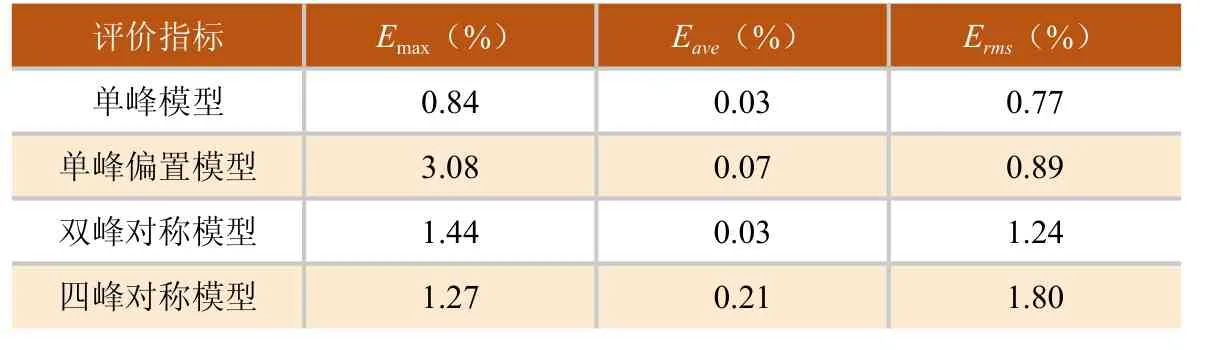
表1 指数SVD重建误差

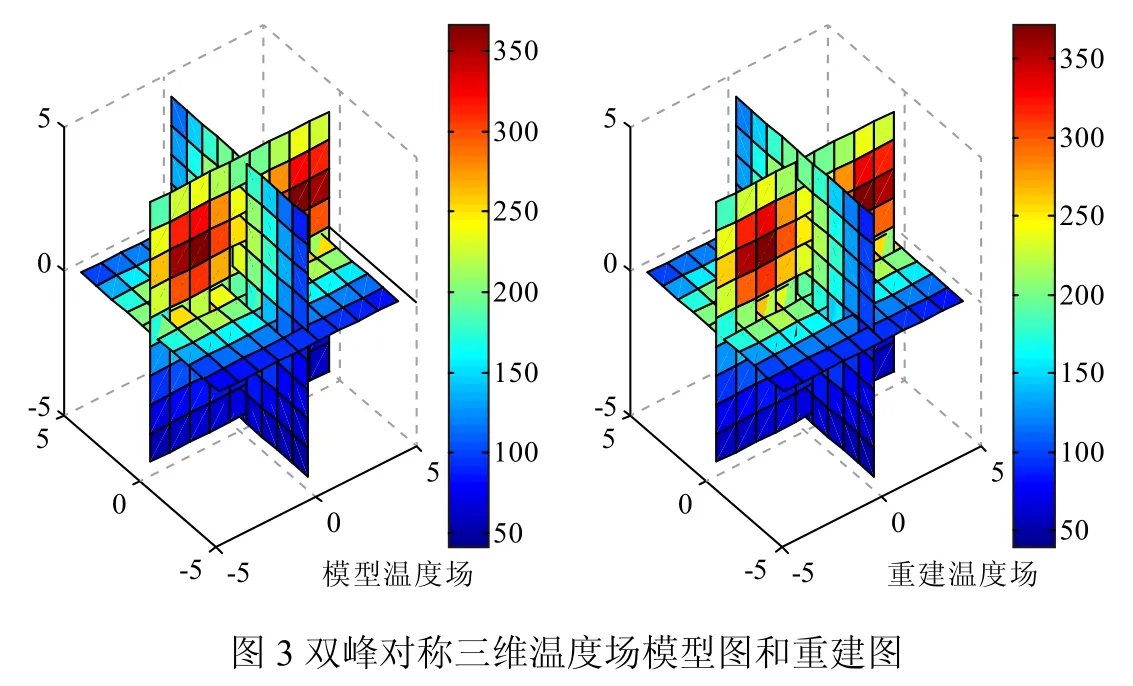
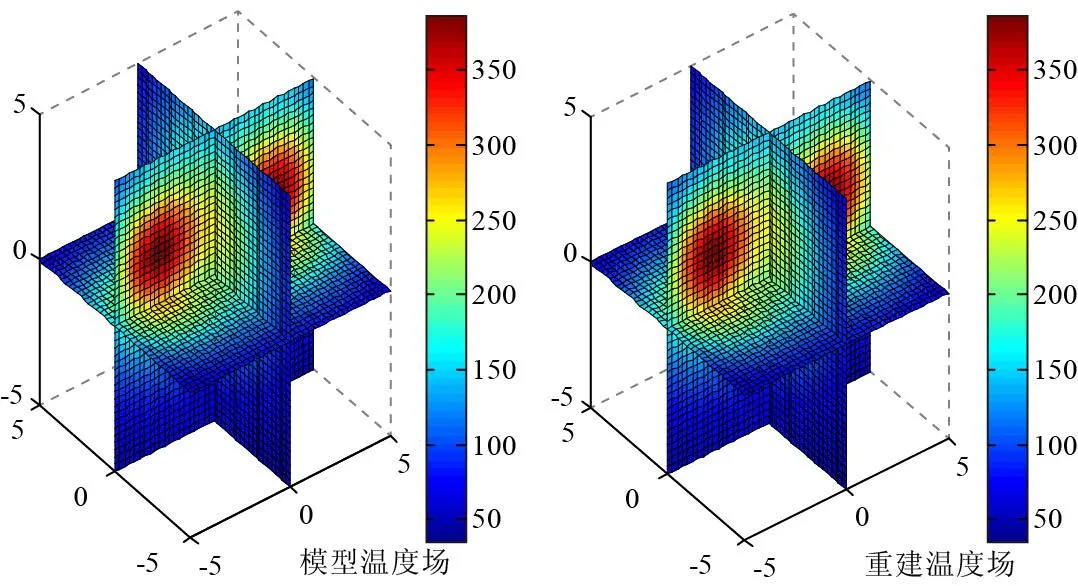
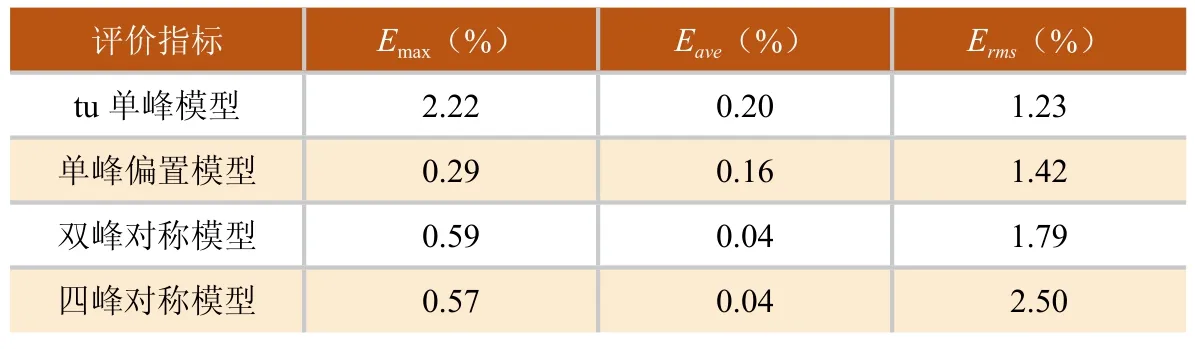
表2 Kriging模型插值误差