圆钢管混凝土柱-H钢梁内隔板式节点抗连续倒塌机理研究

史艳莉, 石晓飞， 王文达， 王景玄， 李华伟

(兰州理工大学 甘肃省土木工程防灾减灾重点实验室，兰州 730050)



圆钢管混凝土柱-H钢梁内隔板式节点抗连续倒塌机理研究

史艳莉, 石晓飞， 王文达， 王景玄， 李华伟

(兰州理工大学 甘肃省土木工程防灾减灾重点实验室，兰州 730050)

为研究圆钢管混凝土柱-H钢梁内隔板式节点抗连续倒塌工作机理，以中柱失效工况下的节点作为研究对象，采用ABAQUS建立了双半跨单柱型梁柱节点模型，在节点柱顶端进行位移加载，得到了节点的承载力曲线、破坏形态以及抗力机制曲线等，在此基础上对影响组合节点抗倒塌承载力的8个关键性参数进行分析，包括钢梁强度、钢管强度、混凝土强度、内隔板强度、柱含钢率、内隔板厚度、内隔板宽度以及跨高比。结果表明，内隔板式节点破坏是从梁机制阶段到悬链线机制阶段再到破坏阶段的发展过程；对节点参数分析可知增大钢梁强度和减小跨高比可显著的提高节点倒塌抗力，增大内隔板的强度、宽度和厚度节点倒塌抗力略有降低，其它参数影响不明显。

内隔板式节点；连续倒塌；有限元分析；抗力机制；参数分析

节点作为结构体系中的关键部位，起着连接周围梁柱构件并将上层的力和弯矩传递到下层的作用，目前国内外研究人员对钢管混凝土柱-H钢梁节点进行了大量研究，应用最多的连接方式主要有内隔板式节点和外加强内隔板式节点，其中内隔板式节点由于其节约空间的优点得到了广泛的应用。

美国土木工程师学会ASCE[1]对结构连续性倒塌给出的定义如下：由于突发情况造成结构局部构件损坏，从而导致结构最终造成与初始损坏不成比例的破坏，甚至导致结构大面积或整体坍塌。结构的倒塌和节点的破坏是密切相关的，近些年来国内外的专家学者通过试验和数值模拟等方法针对各类节点的抗连续倒塌展开了大量的研究，也制定了一些分析研究方法，其中GSA2003[2]提出的拆除构件法来分析剩余结构的抗倒塌性能应用最为广泛，国内外学者亦采用此方法展开了大量的试验研究。

YANG等[3-5]研究了中柱失效后连接方式为平端板连接和角钢连接的型钢梁柱节点在竖向荷载作用下对倒塌抗力和梁转角能力的影响，并提出了一种基于组件的用来模拟中柱失效后组合梁柱节点模型，同时通过数值模拟与试验结果对比分析了节点的配筋率、梁长细比等参数对节点抗力的影响；GUO等[6]设计了5个尺寸相同的带楼板的型钢梁柱节点，在其上施加正、负弯矩和梁端张拉应力的组合荷载，探讨了悬链线机制的形成以及对延性和承载力的影响，并证实了中柱失效后悬链线机制是一种可靠的备用传力路径；王伟等[7-9]建立了双半跨单柱型梁柱子结构，研究了梁柱连接方式(全焊接和栓焊混合连接)、腹板螺栓排列方式对钢管柱-H钢梁节点进行了试验研究，得出了在荷载作用下节点破坏的演化全过程；霍静思等[10]采用落锤冲击的方法研究了扇形和扩大型过焊孔构造的钢框架梁柱节点子结构试件的倒塌全过程，证实了节点的过早破坏会限制悬链线效应的发展，导致无法充分发挥材料的受拉性能；王宁等[11]用ABAQUS对全焊接和栓焊混合连接的钢框架节点抗冲击性能试验进行数值模拟研究，表明显示求解方法可较好地模拟节点的破坏全过程；秦希等[12]模拟了3种不同构造(窄盖板、较宽梯形盖板及较宽梯形盖板、梁下翼缘局部增大)的隔板贯通式全螺栓节点在抵抗连续倒塌工况时的倒塌机理和破坏模式，并研究了上述不同参数对节点倒塌抗力的影响。

以上研究结果表明中柱失效后的型钢梁柱节点和钢管柱-H钢梁节点抗连续倒塌主要经历了倒塌抗力由梁受弯机制提供到悬链线受拉机制提供的一个演变过程，但目前对钢管混凝土柱-H钢梁内隔板式节点尚缺乏研究。因此本文研究对象为圆钢管混凝土柱-H钢梁内隔板式节点抗连续倒塌机理，以ABAQUS为工具在中柱顶端采用位移加载的方式模拟上部结构荷载传递，分析节点在受力过程中的荷载-位移曲线、核心区全过程破坏形态以及抵抗竖向荷载作用下的倒塌抗力机制等，以期为工程实践提供参考价值。

1 计算模型的选取

1.1 模型参数

参照某实际工程设计了双半跨单柱型节点有限元模型，并根据《钢管混凝土结构技术规程》(CECS28：2012)[13]得到节点模型的设计尺寸，圆钢管柱截面规格为Ø400 mm×10 mm，H型钢梁截面规格为H400 mm×200 mm×8 mm×13 mm，内隔板宽度为90 mm，内隔板厚度为13 mm，模型中所用钢材均为 Q345B，弹性模量Es=206 000 MPa，钢管柱内填充强度等级为C40的素混凝土。梁上下翼缘与腹板、钢梁与钢管柱以及钢管柱和内隔板之间连接均采用全焊接的连接方式。其中柱高H=3 000 mm，梁跨度L=4 500 mm，梁跨高比l/h为11. 25，CJ-I节点计算模型图如图1，节点构造详图如图2。

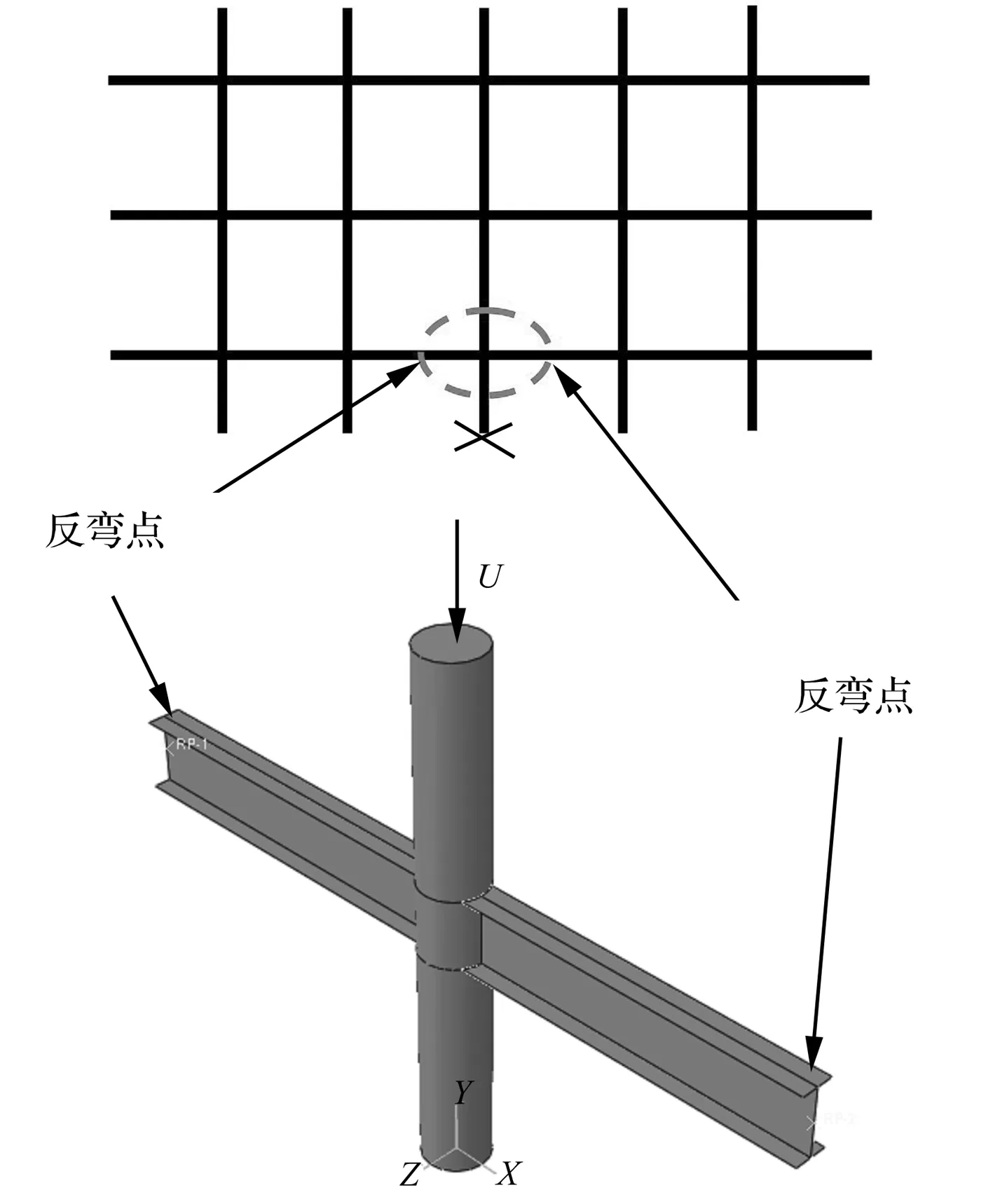
图1 节点模型的选取Fig.1 Selection of the joint model

图2 模型构造详图(mm)Fig.2 Model construction details(mm)

1.2 单元类型的选取和接触的定义

本文采用ABAQUS对圆钢管混凝土柱-H钢梁内隔板式节点进行有限元分析，为了满足计算精度和计算效率，应对材料单元类型进行适当的选取。

混凝土材料选用8节点六面体线性完全积分(C3D8)单元，该单元可以真实的反应出模拟对象在三维空间中的受力过程和变形形态。由于钢材沿厚度方向的尺寸远小于其整体尺寸，因此为了提高计算速度，钢管、钢梁和内隔板等钢材用4节点四边形有限薄膜应变线性完全积分壳(S4)单元。

本文中各构件之间的接触定义如下：钢管和混凝土之间采用面-面接触(Surface-to-surface contact)，钢管和钢梁、钢管和内隔板之间采用绑定(Tie)接触，内隔板与混凝土之间采用嵌入式(Embedded)接触。边界条件定义为节点两侧钢梁端部模拟反弯点处作为铰接连接，柱顶端作为加载端只有竖向变形，柱底端作为自由端用以模拟失效后的中柱，采用线性加载的加载方式对中柱顶端进行位移加载，如图1所示。

1.3 材料本构模型

1.3.1 混凝土本构模型

本文采用ABAQUS软件建模分析，因此材料模型的选用应符合软件特点。柱内核心混凝土受到钢管壁的约束作用，受力较复杂，需考虑到钢管对核心混凝土的约束效应。本文核心混凝土受压本构关系模型采用韩林海[14]提出的模型，其表达式如式(1)所示。

(1)

当混凝土受拉时，采用能量破坏准则来定义混凝土的受拉软化性能，具有较好的收敛性。此准则定义混凝土开裂单位面积作为材料参数，基于脆性破坏的概念，采用应力-断裂能关系来描述混凝土在拉力作用下材料的脆性性能。关于断裂能Gf(混凝土单位面积内产生一条连续裂缝所需能量)的取值，C20混凝土取0.04 N/mm，C40混凝土取0.12 N/mm，中间断裂能的取值采用线性插值进行计算[14]。

1.3.2 钢材本构模型

钢管、钢梁和内隔板的本构关系模型采用基于Esmaeily和Xiao[15]提出的受拉受压骨架线模型，并通过引入参数k1、k2、k3来控制加载骨架线的形状作为钢材的本构模型，表达式为:

(2)

式中：Es为钢材弹性模量；fy和ε为钢材的屈服强度和屈服应变；k1为钢材的强化段起点应变与屈服应变的比值，k2为钢材峰值应变与屈服应变比值，k3为钢材峰值应力与屈服强度比值。k1、k2、k3的具体数值可以根据材性试验计算得出，本文对于钢材材性的统一取值为k1=10，k2=100，k3=1.6。图3为钢材单轴本构模型骨架线曲线。

图3 钢材单轴本构模型Fig.3 Uniaxial constitutive law of steel

2 算例验证

为验证本文所选各材料本构模型的正确性和计算方法的合理性，分别选取了钢管柱-钢梁节点、型钢梁柱节点以及钢框架、钢筋混凝土框架结构的倒塌试验进行数值模拟验证，模拟结果与试验曲线对比结果如下。

2.1 钢管柱-钢梁节点倒塌试验模拟

对王伟等[8]圆钢管柱-H钢梁外环板式节点试验进行计算模拟，钢管柱截面为Ø351 mm×12 mm，钢梁截面尺寸为HW300 mm×150 mm×6 mm×8 mm，外环板厚度与钢梁翼缘相同，环板外伸宽度为25 mm，钢管和钢梁钢材均为Q345B。在用ABAQUS进行模拟时，节点边界条件为铰接连接，钢管、钢梁与环板钢材均采用壳体(S4)单元建模，有限元模拟结果与试验结果对比如图4所示。

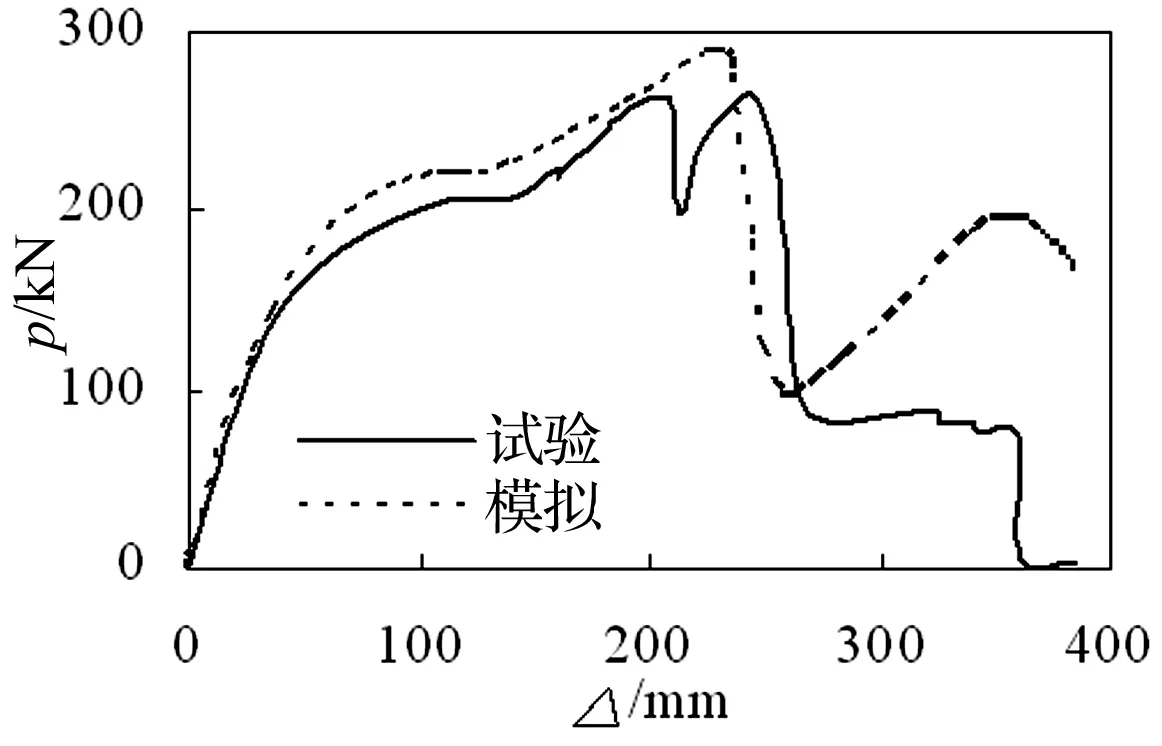
图4 钢管柱-钢梁节点模拟结果与试验对比Fig.4 Comparison between FEM and H-beam to steel tubular column joint experiment results

2.2 型钢梁-柱节点倒塌试验模拟

对GUO等[6]中的1/3缩尺带楼板型钢梁柱节点在正、负弯矩下的倒塌试验进行了数值模拟，柱尺寸为HW200 mm×200 mm×8 mm×12 mm，梁尺寸为HW200 mm×100 mm×5.5 mm×8 mm，钢筋混凝土楼板厚度为100 mm，配筋率为0.85%，建模时板内钢筋选用T3D2单元，边界条件为铰接接触。分别选取了正弯矩作用下的节点RJS与负弯矩作用下的节点RJH进行建模分析，有限元模拟结果与试验结果对比如图5所示。

图5 型钢梁-柱节点模拟结果与试验对比Fig.5 Comparison between FEM and H-beam-to-column joints experiment results

2.3 钢框架结构倒塌试验模拟

对GUO等[16]1/3缩尺的带楼板单层4跨型钢梁柱组合框架结构倒塌试验进行模拟验证，柱高为1 100 mm，跨度为2 000 mm，假定中柱提前失效。钢材强度等级均为Q235，钢梁尺寸为HW200 mm×100 mm× 5.5 mm×8 mm，钢柱尺寸为HW200 mm×200 mm×8 mm×12 mm，混凝土楼板采用强度等级为C30的混凝土，其中钢筋采用HPB235级，用T3D2类型单元，模拟结果与试验结果对比如图6所示。

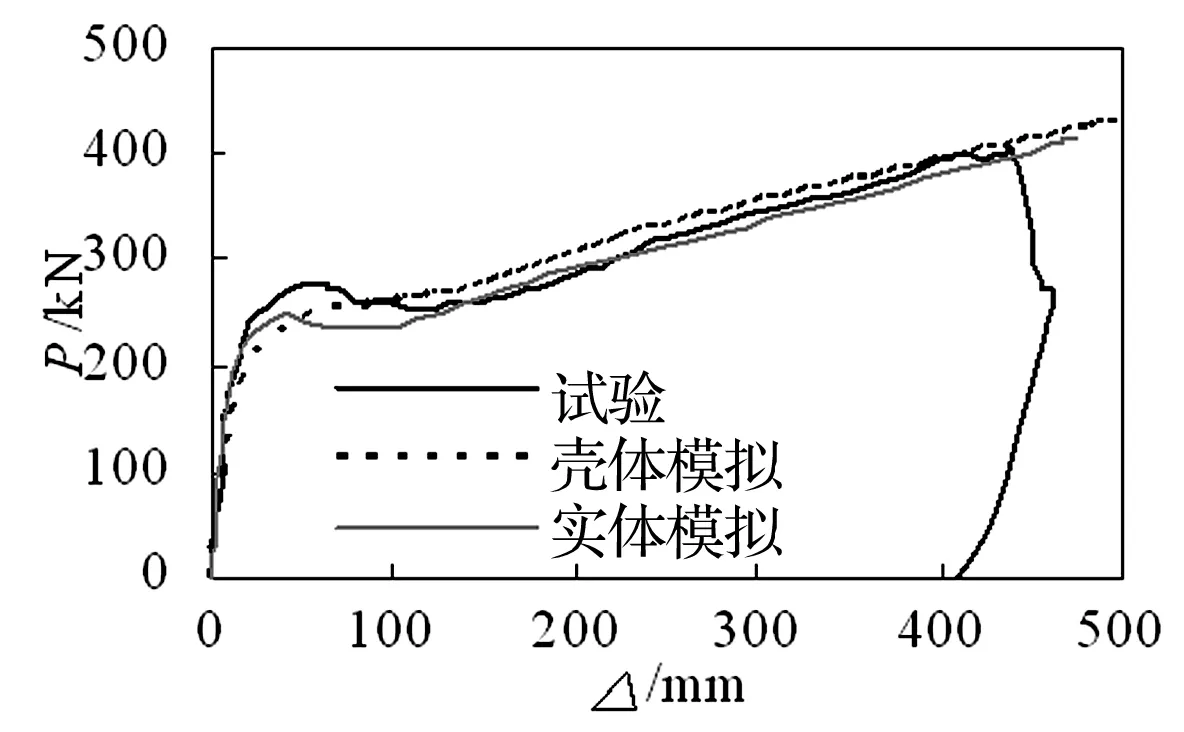
图6 钢框架模拟结果与试验结果对比Fig.6 Comparison between FEM and steel-frame experiment results

2.4 钢筋混凝土框架结构倒塌试验模拟

对易伟建等[17]中1/3缩尺的3层4跨钢筋混凝土框架结构拟静力倒塌试验进行模拟，跨度为2 667 mm，底层层高为1 567 mm，其余层高为1 100 mm。中柱底端用千斤顶逐渐卸载以模拟柱失效过程，通过试验得到了中柱轴力随卸载位移的关系曲线。在用ABAQUS进行模拟时，各材料的单元选取与前述相同，有限元模拟与试验结果对比如图7所示。

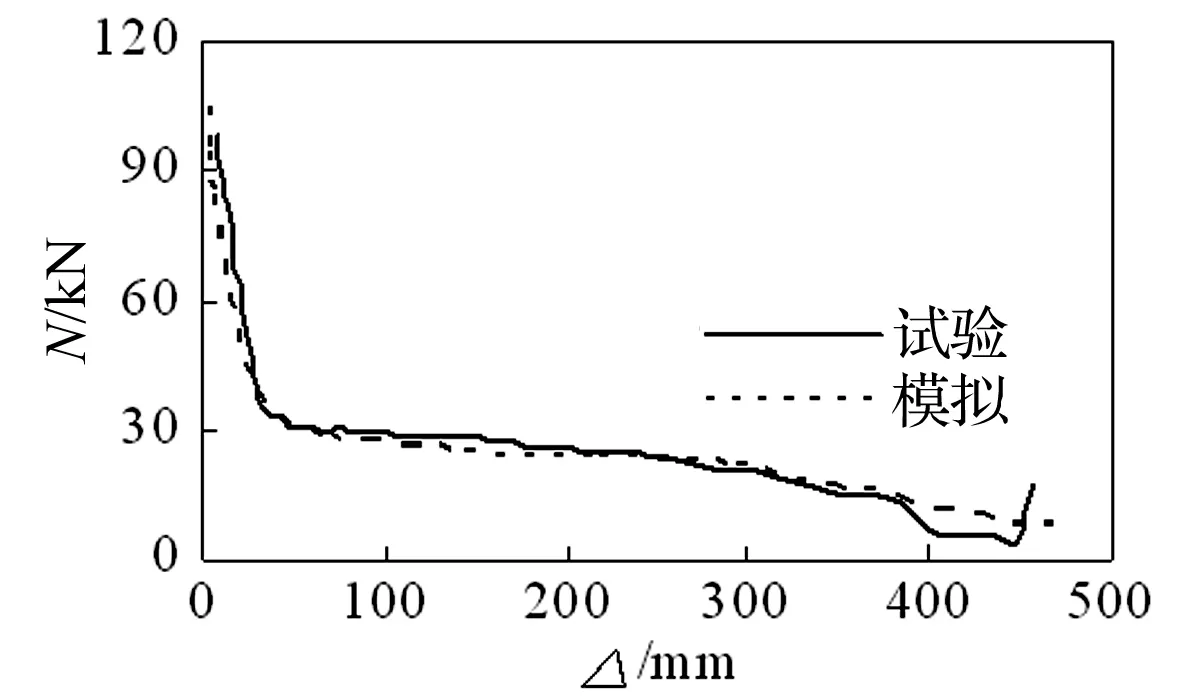
图7 钢筋混凝土框架有限元模拟结果与试验结果对比Fig.7 Comparison between FEM and RC frame experiment results

从以上对节点及框架结构倒塌试验的数值模拟结果可以看出有限元模拟结果与试验结果吻合较好，这说明本文所选各材料本构模型及计算方法能准确的反应出各个构件在试验时的受力形态，因此，本文采用此方法对钢管混凝土柱-H钢梁内隔板式节点抗连续倒塌性能进行分析研究。

3 倒塌全过程机理分析

3.1 倒塌判别准则

自1968年英国Ronan Point事件发生以后，一些国家和机构开始制定结构倒塌判别准则，较为合理的是采用节点梁的相对变形值来判定。本文对节点倒塌失效的判别依据为美国GSA2003[2]规定与节点相连梁的转角θ超过0.21 rad即视作倒塌。

3.2 荷载-位移曲线

根据前述位移加载方法在有限元软件ABAQUS中对节点模型在柱顶端进行加载，根据前述倒塌判别准则可知节点的倒塌临界位移为473 mm，由此可以得出典型CJ-I节点的荷载-位移曲线如图8所示。

图8 典型节点的荷载-位移曲线Fig.8 Load-displacement curves of joints

由图8可知， CJ-I节点在加载初期时，柱顶反力随加载位移的增加表现为线性增长；当柱顶位移增加到24 mm(A点，θ=0.011 rad)时，曲线的刚度出现了明显下降，靠近柱的钢梁下翼缘钢材出现了受拉屈服(图9(a))；随着荷载的增大，柱顶竖向位移达到462 mm(B点，θ=0.205 rad)时梁下翼缘被断裂(图9(b))，此时荷载达到最大值1 479 kN并迅速下降48%，此时节点已经达到了GSA2003[2]规定的倒塌状态，此时节点由梁上翼缘及腹板连接处产生的悬链线机制来为节点提供抗倒塌承载力；当加载位移达到686 mm(D点，θ=0.305 rad)时，梁断裂截面已蔓延至上翼缘处(图9(d))，节点承载力迅速降低，此时模型已完全破坏。

3.3 节点核心区变形形态

为探究加载全过程中节点核心区的变形形态，对CJ-I节点核心区纵向应力进行分析，红色与蓝色分别代表受拉与受压，如图9所示。

图9 节点核心区破坏过程模拟Fig.9 Failure process of core area

节点核心区的破坏过程大致可分为四阶段：第一阶段为钢梁下翼缘开始屈服，靠近钢管壁的梁下翼缘钢材在加载初期节点产生小变形时很快发生受拉屈服；第二阶段为钢梁下翼缘被拉裂破坏，随着加载位移增大钢梁变形亦增大，靠近钢管壁的梁下翼缘钢材开始达到极限应力并被拉裂；第三阶段为钢梁腹板开始发生拉裂破坏，随着钢管柱竖向位移的增大，与钢管壁连接处梁下翼缘已全部被拉断，腹板开始被拉裂，拉裂区域开始通过腹板向梁上翼缘蔓延；第四阶段为拉裂区域向上贯通梁腹板基本全部被拉裂，至此时中柱竖向位移已经达到GSA2003[2]规定的473 mm破坏位移而发生倒塌，节点抗倒塌承载力开始出现下降，仅靠钢梁上翼缘产生的悬链线机制来提供。

3.4 节点抗倒塌承载力机制分析

由以上对CJ-I节点在竖向位移作用下的荷载-位移曲线和节点核心区破坏形态分析可知，圆钢管混凝土柱-H钢梁内隔板式节点从受荷初期发生小变形到最终节点发生大变形破坏大致经历了四个受力阶段：梁机制阶段、混合机制阶段、悬链线机制阶段以及破坏阶段，图10为包含四个阶段节点的抗倒塌承载力抗力机制曲线图。

图10 节点抗倒塌承载力机制曲线Fig.10 Resistance mechanism curves of joints

提取钢梁下翼缘梁机制与悬链线机制提供抗倒塌承载力与加载位移之间的关系曲线，正则化后可得到节点抗倒塌承载力机制转换曲线，如图11所示：加载初期梁机制提供倒塌抗力增加较快，悬链线机制提供倒塌抗力增加缓慢；随着加载的进行梁机制提供倒塌抗力达到峰值并开始下降， 此时悬链线机制提供倒塌抗力迅速上升，达到峰值后开始也出现下降。在整个加载过程中梁机制与悬链线机制共同为节点提供倒塌抗力，二者相辅相成，又表现出了“此消彼长”的规律。

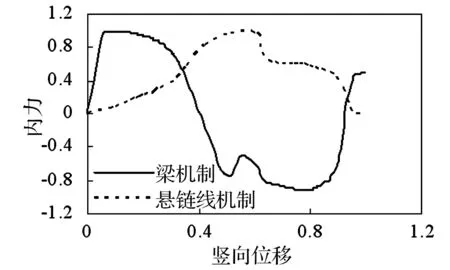
图11 典型节点正则化抗力机制转换曲线Fig.11 Resistance mechanism transformation curves

3.5 节点竖向位移分布

将CJ-I节点两侧钢梁翼缘平均3等分，得到8个测点，对节点进行位移加载，可以得到整个加载过程中各个测点的位移变化，从而得到节点的竖向位移分布图，如图12所示。从图中可以看出，当加载位移小于50 mm时，此时节点竖向位移分布连线基本呈弧线状，说明此时节点尚处于弹性变形阶段，即位于图8中的OA段；随着加载位移的增大，各测点位移分布连线逐渐呈折线状，且以中间钢管左右对称，此时节点已经由梁机制阶段逐渐过渡到混合机制阶段并最终到悬链线机制阶段，此时节点的荷载-变形关系已由AB段发展至BC段，直至节点发生破坏。

图12 节点竖向位移分布图Fig.12 Joints vertical displacement distribution

3.6 钢梁截面应变分布

为研究加载过程中各时刻钢梁截面应变的发展情况，在距离钢梁端部200 mm处各取一个截面(图13)，将钢梁截面沿高度方向分为四段，由此可以得到钢梁截面1和截面2在钢梁下翼缘被拉裂前沿梁轴向应变的变化趋势，应变以受拉为正受压为负，如图14所示。

图13 截面位置Fig.13 Section position

图14 CJ-I节点应变沿钢梁高度变化曲线Fig.14 CJ-I beam strain curves along with height

由图14可以看出，CJ-I节点钢梁截面1处在受荷初期表现为上翼缘受压，下翼缘受拉，钢梁中性轴由截面中间位置处向上移动；随着加载位移的增大，钢梁下翼缘拉应变增加较快，上翼缘受压区逐渐减小而下翼缘受拉区增大，截面1位置处下翼缘钢材很快达到极限拉应变而被拉裂，钢梁截面应变变化趋势与前述图9中节点核心区全过程破坏形态相对应，而截面2处钢梁在加载位移达到200 mm时钢梁即已进入到全截面受拉状态。

4 节点参数分析

为进一步研究影响圆钢管混凝土柱-H钢梁内隔板式节点抗连续倒塌承载力的因素，本文对节点的8个关键性参数进行了对比分析。参数包括材料参数如钢梁强度(fy)、钢管强度(fy)、混凝土强度(fcu)，内隔板强度(fy)，几何参数如柱含钢率(α)、内隔板厚度(t)、内隔板宽度(b)以及钢梁高度(h)，分析结果如下。

4.1 钢梁强度

同时改变钢梁翼缘和腹板材料的屈服强度fy，计算后可以得到节点的荷载-位移曲线，如图15所示。由图可知，当钢梁强度从235 MPa增加到420 MPa时，节点梁机制和悬链线机制提供抗倒塌承载力均有明显提高，梁机制提供抗倒塌承载力分别增加了41%、60%、79%，悬链线机制提供抗倒塌承载力增加了87%、122%、150%，悬链线机制提供抗倒塌承载力提高更为显著。这是因为随着钢梁强度的增加，钢梁的抗弯性能和抗拉性能均有显著的增加，而节点抗倒塌承载力主要是由梁受弯机制和悬链线抗拉机制共同提供的。

图15 钢梁强度对节点抗力的影响对比Fig.15 Beam strength impact on resistance capacity

4.2 钢管强度

钢管强度对节点抵抗连续倒塌的影响主要体现在节点核心区处的钢管部分，通过改变其屈服强度fy可以得到不同钢管强度对节点倒塌抗力的影响曲线，如图16所示，从曲线中可知总体上钢管材料屈服强度的改变对节点抗倒塌承载力影响并不明显，这是因为节点倒塌抗力主要是由钢梁和核心区二者组成的悬索通过梁机制和悬链线机制来提供，最主要还是由钢梁提供，钢管仅承受钢梁对其沿径向向外拉伸的作用，且钢梁上下翼缘处对应处还有内隔板对其的约束作用，因此在整个受力过程中钢管的变形较小作用有限。

图16 钢管强度对节点抗力的影响对比Fig.16 Tube strength impact on resistance capacity

4.3 混凝土强度

图17为不同强度的混凝土对节点抗倒塌承载力的影响对比。

从图中可以看出混凝土强度的改变对节点抗倒塌承载力基本无影响，这是因为混凝土在加载全过程中主要处于受压状态，而节点抗倒塌承载力主要是由梁受弯机制和悬链线受拉机制共同提供。

图17 核心混凝土强度对节点抗力的影响对比Fig.17 Core concrete strength impact on resistance capacity

4.4 内隔板强度

图18为改变内隔板的屈服强度fy后节点的荷载-位移曲线。由图可知，内隔板强度从235 MPa增加到420 MPa时，梁机制提供抗倒塌承载力影响变化不明显，而悬链线机制提供抗倒塌承载力均有一定程度的下降，下降幅度分别为5.8%、6.9%、8.9%。这是因为，内隔板强度增大后节点核心区的刚度就越大，在受力后期节点发生大变形时核心区变形减小，相当于削弱了梁的强度，限制了节点悬链线机制的发展，节点过早的发生破坏。

图18 内隔板强度对节点抗力的影响对比Fig.18 Inner-diaphragm strength impact on resistance capacity

4.5 柱含钢率

钢管含钢率的表达式为：α=As/Ac，其中As为钢管横截面面积，Ac为核心混凝土横截面面积。

通过改变钢管壁厚来改变柱截面的含钢率，计算结果如图19所示。随着含钢率的增加，节点梁机制提供抗倒塌承载力基本无变化，悬链线机制提供抗倒塌承载力分别增加了2.1%、4.2%、6.2%，在整个受力过程中钢管与钢梁共同组成一根“悬索”通过受拉来为节点提供抗倒塌承载力，钢梁对节点承载力影响较大，而钢管影响则很有限。

图19 钢管含钢率对节点抗力的影响对比Fig.19 Steel ratio impact on resistance capacity

4.6 内隔板厚度

不同厚度的内隔板对节点抗倒塌承载力的影响对比如图20所示。由图可知，随着内隔板厚度的增加，节点梁机制提供抗倒塌承载力变化不明显，而悬链线机制提供抗倒塌承载力则降低，降低幅度分别为1.9%、7.1%、9.2%、12.5%，原因同内隔板强度影响类似。

图20 内隔板厚度对节点抗力的影响对比Fig.20 Inner-diaphragm thickness impact on resistance capacity

4.7 内隔板宽度

不同宽度的内隔板对节点抗倒塌承载力影响如图21所示。

图21 内隔板宽度对节点抗力的影响对比Fig.21 Inner-diaphragm width impact on resistance capacity

从图21中可以看出，与内隔板厚度对节点倒塌抗力的影响相似，随着内隔板宽度的增加，节点悬链线机制提供抗倒塌承载力也呈现出降低的趋势，降低幅度分别为0.4%、6.9%、12.2%。这也是因为内隔板宽度的增加增大了节点核心区的刚度，限制了节点悬链线机制的开展。

4.8 跨高比

节点的跨高比定义为节点钢梁跨度l与钢梁高度h的比值。图22为通过改变钢梁高度来对比不同跨高比对节点抗倒塌承载力的影响。

图22 跨高比对节点抗力的影响对比Fig.22 span-depth ratio impact on resistance capacity

由图可知，随着跨高比的降低，节点由梁机制提供的抗倒塌承载力增加较明显，增加幅度分别为11.3%、24.7%、60.5%，而悬链线机制提供抗倒塌承载力变化不大，但悬链线机制提供抗力峰值处应的位移则明显变小，对应的分别为469 mm、454 mm、427 mm、367 mm。这是因为随着高度的增大钢梁截面惯性矩增大，从而增大了梁受弯机制提供的抗力。但这会导致钢梁下翼缘过早形成了塑性铰，随着加载的进行更多钢梁截面屈服以致被拉裂。

5 结 论

通过对圆钢管混凝土柱-H钢梁内隔板式节点进行以上抗连续倒塌工作机理以及参数分析等数值模拟分析，可初步得出以下结论：

(1) 节点倒塌抗力由梁机制和悬链线机制作用共同提供，但主要还是由悬链线机制提供，因此在节点设计时应最大限度的发挥悬链线机制的悬索作用，为梁柱子结构受力后期大变形情况下提供连续且稳定的承载力；

(2) 钢梁下翼缘与钢管壁连接处为薄弱部位，相比于钢梁下翼缘塑性铰处更易发生破坏，从而导致梁-柱拉结作用遭到削弱并最终引发节点发生倒塌破坏；

(3) 由参数分析结果可知，在本文参数变化范围内，钢梁强度、跨高比对节点倒塌抗力影响较明显；内隔板强度、厚度和宽度对节点倒塌抗力影响较小；而钢管强度、混凝土强度以及柱含钢率对节点倒塌抗力基本无影响。

[1] ASCE7—05, Minimum design loads for building and other structures[S]. Reston, VA:American society of Civil Engineers, 2005.

[2] GSA—2003, Progressive collapse analysis and design guidelines for new federal office buildings and major modernization project [S]. US General services Administration, 2003.

[3] YANG B, TAN K H. Experimental tests of different types of bolted steel beam-column joints under a central-column-removal scenario [J]. Engineering Structures, 2013, 54: 112-130.

[4] YANG B, TAN K H. Behavior of composite beam-column joints in a middle-column-removal scenario: experimental tests[J]. Journal of Structural Engineering, 2014,140(2):1-20.

[5] YANG B, TAN K H, XIONG G. Behavior of composite beam-column joints under a middle-column-removal scenario Component-based modelling[J]. Journal of Constructional Steel Research, 2015, 104: 137-154.

[6] GUO L H, GAO S, WANG Y Y, et al. Tests of rigid composite joints subjected to bending moment combined with tension[J]. Journal of Constructional Steel Research, 2014, 95: 44-55.

[7] 王伟，李玲，陈以一．方钢管柱-H形梁栓焊混合连接节点抗连续性倒塌性能试验研究[J]．建筑结构学报，2014，35(4)：92-99．

WANG Wei, LI Ling, CHEN Yiyi. Experimental investigation on progressive collapse behavior of WUF-B joints between SHS column and H beam [J]. Journal of Building Structures, 2014, 35(4): 92-99.

[8] 王伟，李玲，陈以一，等．圆钢管柱-H形梁外内隔板式节点抗连续性倒塌性能试验研究[J]．建筑结构学报，2014，35(7)：26-33．

WANG Wei, LI Ling, CHEN Yiyi,et al. Experimental study on progressive collapse behavior of CHS column-to-H beam joints with outer-diaphragm [J]. Journal of Building Structures, 2014, 35(7): 26-33.

[9] 王伟，严鹏，李玲．用于钢框架连续性倒塌分析的梁柱栓焊节点模型研究[J]．工程力学，2014,31(12)：119-125．

WANG Wei, YAN Peng, LI Ling. Research on joint models of welded flange-bolted web joint for progressive collapse analysis of steel frames[J]. Engineering Mechanics, 2014, 31(12): 119-125.

[10] 霍静思，王宁，陈英．钢框架焊接梁柱节点子结构抗倒塌性能试验研究[J]．建筑结构学报，2014，35(4)：100-108．

HUO Jingsi, WANG Ning, CHEN Ying. Experimental study on collapse resistance of welded beam-column joint substructure of steel frame based on seismic design [J]. Journal of Building Structures, 2014, 35(4): 100-108.

[11] 王宁，陈英，霍静思．钢框架梁柱节点子结构抗冲击力学性能有限元仿真研究[J]．振动与冲击，2015，34(18)：51-56．

WANG Ning, CHEN Ying, HUO Jingsi. FE analysis on dynamic behaviors of beam-column joint in steel frame[J]. Journal of Vibration and Shock, 2015, 34(18): 51-56.

[12] 秦希，王伟．隔板贯通式全螺栓节点抗连续性倒塌性能数值模拟分析[J]．振动与冲击，2015，34(10)：68-75．

QIN Xi, WANG Wei. Numerical simulation for progressive collapse behavior of through diaphragm bolted beam-column joints[J]. Journal of Vibration and Shock, 2015, 34(10):68-75.

[13] 中国工程建设标准化协会．钢管混凝土结构设计与施工规程:CECS28—2012[S]．北京：中国计划出版社，2012．

[14] 韩林海．钢管混凝土结构-理论与实践[M]．北京：科学出版社，2007．

[15] ESMAEILY A, XIAO Yan. Behavior of reinforced concrete columns under variable axial loads: analysis [J]. ACI Structure Journal, 2005, 102(5): 736-744.

[16] GUO L H, GAO S, FU F, et al. Experimental study and numerical analysis of progressive collapse resistance of composite frames [J]. Journal of Constructional Steel Research, 2013, 89: 236-251.

[17] 易伟建，何庆锋，肖岩．钢筋混凝土框架结构抗倒塌性能的试验研究[J]．建筑结构学报，2007,28(5)：104-109．

YI Weijian, HE Qingfeng, XIAO Yan. Collapse performance of RC frame structure[J]. Journal of Building Structures,2007, 28(5): 104-109.

Progressive collapse mechanism for H-beam—concrete-filled steel tubular column connections with steel inner-diaphragm joints

SHI Yanli, SHI Xiaofei, WANG Wenda, WANG Jingxuan, LI Huawei

(Gansu Provincial Key Laboratory of Disaster Prevention and Mitigation in Civil Engineering of Gansu ProvinceLanzhou University of Technology, Lanzhou 730050, China)

To investigate the progressive collapse resistance mechanism for H-beam—concrete-filled steel tubular(CFST) column connections with inner-diaphragmjoints, a finite element model(FEM) for two half-span joint under the middle-column removal condition was established using ABAQUS. The displacement control loading method was used in FE andysis. The resistance capacity curves, failure modes and resistance mechanism curves of joints were calculated. The parametric analysis of H-beam—CFST column connections with inner-diaphragmjoints was conducted to find influence laws of different parameters, such as, beam strength, tube strength, core concrete strength, inner-diaphragm strength, steel ratio of column, thickness and width of inner-diaphragm, and span-depth ratio on joints’ anti-collape capacity. The results indicated that the joints’ failure evolution modes develop from beam flexural stage to catenary stage and damaged stage ultimately; increasing beam strength and decreasing span-depth ratio can obviously improve joints’ resistant collapse capacity, increasing inner-diaphragm strength, width and thickness can reduce their resistant collapse capacity, and other parameters have no obvious influences.

inner-diaphragm joints; progressive collapse; finite element analysis; resistance mechanism; parametric analysis

国家自然科学基金(51268038)；兰州理工大学“红柳杰出人才培养计划”(J201305)

2015-09-01 修改稿收到日期：2015-10-10

史艳莉 女，博士生，副教授，1977年生

王文达 男，博士，教授，1976年生

TU398

A

10.13465/j.cnki.jvs.2016.19.025