剪式悬架座椅等效刚度阻尼的计算与分析

水奕洁， Subhash Rakheja， 上官文斌

(华南理工大学 机械与汽车工程学院，广州 510640)



剪式悬架座椅等效刚度阻尼的计算与分析

水奕洁， Subhash Rakheja， 上官文斌

(华南理工大学 机械与汽车工程学院，广州 510640)

推导了座椅悬架的等效刚度和等效阻尼，建立了座椅-座椅悬架-人体耦合二自由度理论简化模型，计算分析了系统的传递函数。在建立的模型的基础上，讨论了座椅悬架结构的变化对系统响应的影响，讨论了弹簧倾角、阻尼器倾角，以及连杆的长度和倾角对座椅悬架系统等效刚度及其变化、等效阻尼和传递函数的影响。所建立的理论模型，可为进行座椅悬架结构的优化设计提供分析模型。

座椅-座椅悬架-人体系统；等效刚度；等效阻尼；传递函数

研究表明，职业驾驶员因日常工作中长期连续暴露在来自路面激励引起的全身振动环境中[1-5]，不仅工作效率大大降低，而且会诱发各种职业病，如劲椎腰椎疾病。因此，座椅悬架作为衰减振动和冲击的最后一道系统被广泛应用在采矿业、建筑业等工程车辆上[6]，来改善驾驶员的工作环境，提高车辆的乘坐舒适性。

SUBHASH等[7]对座椅悬架进行了较为深入的研究。研究表明，座椅与座椅悬架系统的响应一般可以分为三个阶段：第一个阶段是当激励为小幅值或低频率振动时，由于摩擦作用，整个悬架系统处于锁止状态；随着振动幅值和频率的增加，系统进入第二阶段，放大或衰减区域；当激励的幅值继续增大时，会反复碰到系统的限位块，引起很大的冲击。为了衰减冲击和共振响应，阻尼应选择较大值，但为了衰减高频振动，阻尼值应相对较小，由于这个原因，可控阻尼[8]和磁流变阻尼器的性能及控制原理被广泛研究。

已有研究将座椅-座椅悬架系统-人体耦合模型简化为两自由弹簧质量系统[9]，座椅悬架部分简化为单自由度，坐垫简化为弹簧和阻尼，人体用集中质量代替；还有些将座椅-人体耦合模型简化为五自由[10]或六自由[11]弹簧质量系统，座椅简化为线性单自由度或二自由度，人体简化为四自由度模型。

由于剪式导向支撑机构复杂的动力学特性，上述模型均未考虑具体座椅结构，直接利用弹簧和阻尼的参数，或者实验测量得到的等效刚度[12]建立数学模型，并未从理论上推导悬架结构的刚度和阻尼；此外，工程车辆工作环境差，路面土坡较多，由于空气弹簧压缩段刚度大于拉伸段刚度，会导致座椅悬架在拉伸段行程大于压缩段，在拉伸段时更容易碰到限位块，引起冲击。通过座椅悬架结构的改变，使得系统等效刚度在整个座椅行程中的变化更为平缓,可降低这一现象的发生，国内外针对座椅悬架结构的改变对等效刚度及系统响应的影响的研究较少。

本文推导了座椅悬架结构在在运动过程中等效弹簧力和等效阻尼力的关系式，并由此得到阻尼的等效刚度和等效阻尼。然后利用座椅悬架结构的等效刚度和等效阻尼将座椅-座椅悬架-人体耦合模型简化成两自由弹簧质量系统，并推导了系统的运动微分方程，得到系统传递函数，并与按照实际尺寸建立的三维Adams模型仿真得到的结果对比，验证理论推导的有效性。讨论了弹簧的倾角对系统等效刚度和系统传递函数的影响，阻尼器倾角变化对系统传递函数的影响，以及连杆的长度和倾角变化对悬架结构等效刚度和系统传递函数的影响。

1 座椅悬架等效刚度和等效阻尼的计算

1.1 座椅悬架结构与性能评价参数

座椅悬架由导向支撑机构，弹簧，阻尼器，限位块和坐垫等几部分组成。剪式结构由于结构的稳定和可靠，多用于座椅的支撑和导向。座椅悬架中的弹簧有机械弹簧和空气弹簧两种不同类型，弹簧一般有三种布置形式，分别为基座与上底板之间、剪式臂之间或者剪式臂与基座之间，第三种形式应用较为广泛。阻尼器一般以一定角度布置在交叉臂之间或者基座与上底板之间。

图1 悬架结构简图Fig.1 The diagram of the seat suspension

如图1所示为座椅悬架的示意图，空气弹簧的上端点S连接在导向杆BD上，下端点G固定在基座上，阻尼器的上端点E连接在导向杆BD上，下端点F固定在导向杆AC上。图1中所示为座椅行程的中间位置，取该位置为平衡位置，座椅悬架的结构参数描述如下：平衡位置时基座与上底板之间的距离为H0，设杆长AO=BO=l1，OC=OD=l2，CF=l3，OE=l4，OS=l5，DG=l6，L=l1+l2，点A到上底板质心的水平距离为l7，杆AC、BD与水平方向的夹角为α，CF与水平方向的夹角分别为β，OE和杆BD的夹角为γ，OS和杆BD的夹角为η，弹簧轴线SG与水平方向的夹角为φ，阻尼器与水平方向的夹角为θ。

对图1所示的座椅结构布置形式，在座椅上下运动的过程中，弹簧角度以及阻尼器倾角均会发生变化，使得座椅-座椅悬架系统的等效刚度和等效阻尼产生非线性变化。在座椅-座椅悬架系统的设计中，性能评价参数包括：在座椅上下运动的过程中，等效刚度的变化要小；座椅-座椅悬架-人体耦合系统的固有频率应在1～2 Hz；此外，悬架结构的相对阻尼系数应在0.18～0.35范围内。

1.2 座椅悬架的等效刚度

座椅悬架的等效刚度即为座椅悬架结构在z向发生单位位移时需要在上底板施加的垂向力。

任意瞬时，悬架的变形量为zs，基座到上底板的高度为：

h=H0+zs

(1)

由几何关系可知，悬架运动过程中连杆倾角α满足：

(2)

(3)

本文座椅悬架弹簧为空气弹簧，在座椅运动过程中，空气弹簧内的气体变化过程不是绝对的等温过程也不是绝热的等压过程，而是一个多变过程，多变指数为n，则气压P和体积V满足：

(4)

P0，V0为座椅悬架在平衡位置时，空气弹簧的初始压力和体积，则弹簧力Fs为：

(5)

取座椅运动过程中某一瞬时为研究对象，分析整个座椅悬架结构的受力情况，见图2。

图2 系统受力分析图Fig.2 The force analysis for the seat

A1X=B1Fs

(6)

式中:A1和B1的表达式为：

(7)

对导向杆AC，BD分别进行受力分析，如图3所示。

图3 导向杆受力分析图Fig.3 The force analysis for the linkage

根据X向，Z向力平衡和对点O的力矩平衡，由图3(a)可得：

A2X=0

(8)

式中:A2的表达式为：

A2=

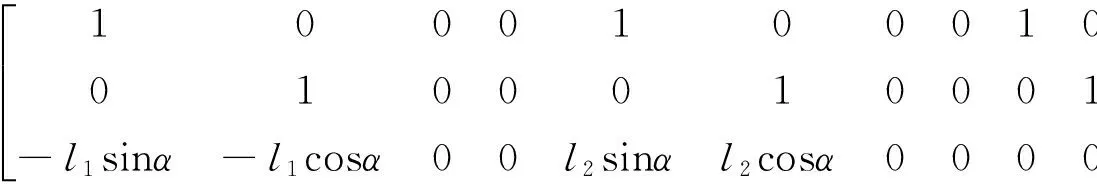
根据X向，Z向力平衡和对点O的力矩平衡，由图3(b)可得：

A3X=B3Fs

(10)

式中:A3和B3的表达式为：

(11)

由B，C两点动摩擦关系式可知：

A4X=0

(12)

式中:A4的表达式为：

(13)

式中，f为滚动摩擦系数。

由式(6)～式(13)有：

(14)

作用在座椅悬架上的等效弹簧力Fse为：

Fse=FAz+FBz

(15)

式(14)中共11个方程，11个未知数，可求得FAz，FBz均为座椅悬架变形量zs的函数，由式(15)可求得座椅悬架结构的等效弹簧力Fse，即可得到等效弹簧力Fse与悬架变形zs的关系曲线，对该曲线求导可得到座椅悬架的非线性等效刚度Ke曲线。

1.3 座椅悬架的等效阻尼及相对阻尼系数

座椅悬架等效阻尼即为座椅悬架结构在z向产生单位速度所需要在上底板施加的垂向力。

1.3.1 阻尼器速度

(16)

座椅导向杆及杆上点的速度分析如图4所示。

图4 座椅导向杆及杆上点的速度分析图Fig.4 The velocity analysis for the linkage

杆AC绕某一瞬心O′(杆AC转动的瞬心,与B点重合)转动的角速度ωAC方向如图4(a)所示，大小为：

(17)

则F点的速度为：

(18)

杆BD绕D点转动的角速度ωBD方向如图4(b)所示，大小为：

(19)

则E点的速度为：

(20)

(21)

1.3.2 等效阻尼及相对阻尼系数

在考虑等效阻尼力时，忽略座椅悬架模型的弹簧力和摩擦力，座椅悬架运动某一时刻，以杆BD为研究对象，分析其受力如图5所示，在该过程中假设A，B，C，D四点垂直方向的力大小相等，固定点A，D水平方向的力忽略不计。

图5 杆BD及杆上点E受力分析图Fig.5 the force analysis for the linkage BD and point E

根据杆BD在O点的力矩平衡有：

FBzl1cosα+FExl4sin(α+γ)+

FDzl2cosα+FEzl4cos(α+γ)=0

(22)

式中:

FEx=Fdampcosθ，FEz=Fdampsinθ

(23)

Fdamp是阻尼器产生的阻尼力，有：

Fdamp=cvEF

(24)

c为阻尼器阻尼，将式(23),(24)代入式(22)即可求得FBz。

作用在上下底板之间的等效阻尼力Fd为：

Fd=2FBz

(25)

(26)

ζ为座椅悬架结构的相对阻尼，则有：

(27)

2 座椅-座椅悬架-人体系统传递特性模型

由以上推导过程可知，座椅的悬架可等效为刚度为Ke，阻尼为Ce的弹簧阻尼系统，再将坐垫考虑成线性的弹簧阻尼Kc和Cc，人体为集中质量mb，则可将座椅-座椅悬架-人体耦合模型等效为二自由度弹簧质量系统，如图6所示。

等效模型的运动微分方程为

(28)

式中:

图6 座椅-座椅悬架-人体模型简化Fig.6 The simplify of the seat, seat suspension and human model

对式(27)进行傅里叶变换，得到Z0到Z的传递函数为：

H=[K-ω2M+jωC]-1[B+jωA]

(29)

在Adams/view中按照座椅处于中间位置时测量得到各部分的尺寸和位置参数建立座椅-座椅悬架-人体二自由度耦合模型，用运动副将各部分连接起来，具体模型如图7所示。

图7 座椅-座椅悬架-人体Adams模型Fig.7 Tthe Adams model ofseat, seat suspension and human

在Adams/vibration模块中，输入通道定义为基座的位移幅值为1 mm，相位为零的扫频激励，输出通道定义为上底板和人体垂向的位移响应，进行振动分析得到传递函数，并将仿真结果与理论推导式(29)所得结果进行对比，传递函数基本一致，根据实际传递到座椅振动清考，考虑的频率范围为0～10 Hz，在该频率段只有一个峰值，对于两自由度模型，第二个共振峰共振峰为上底板共振，对文中研究的人体振动响应意义不大，不予考虑。在该频率范围，曲线的峰值频率与幅值对比见表2，由式(27)计算得到悬架结构的相对阻尼为0.24。模型中的基本参数见表3。

表2 传递函数峰值频率和幅值对比

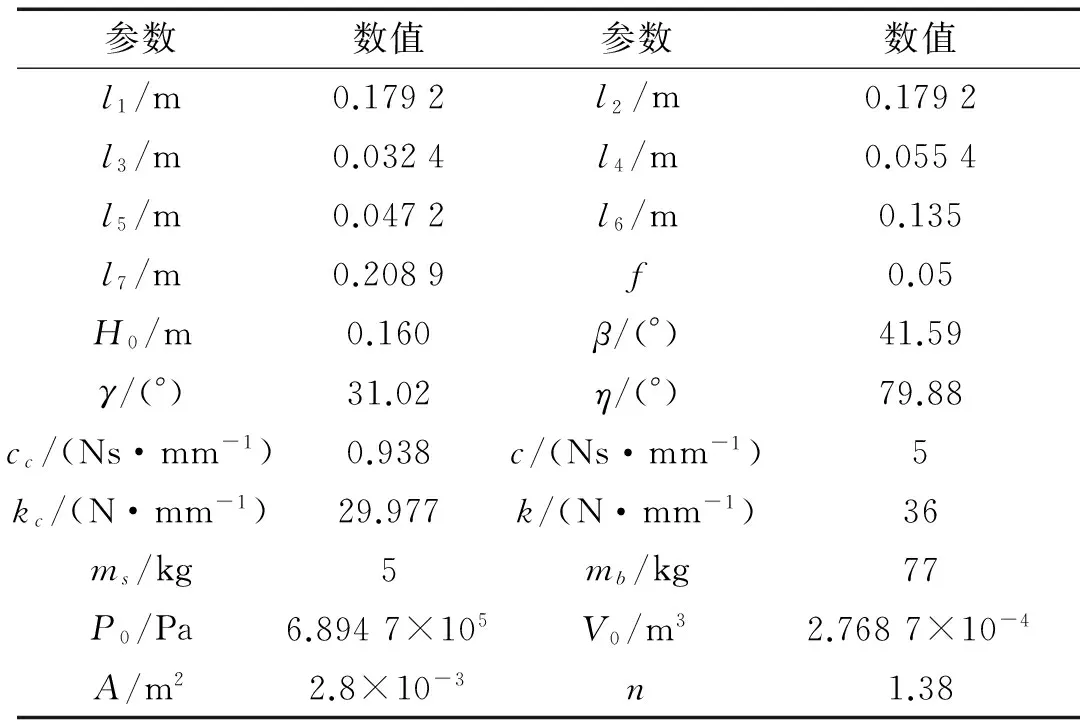
表3 模型基本参数

由表2中数据可知，两种方法得到的传递函数基本一致，峰值处频率有0.04 Hz，幅值有0.1的误差。分析误差产生的原因： Adams中模拟的是实际的运动情况，在运动过程中弹簧和阻尼的角度会发生变化，而等效过程中仅考虑座椅悬架结构在平衡位置作小幅振动，忽略角度的变化。通过两种不同方法得到的传递函数的对比，在误差允许范围内，可验证刚度、阻尼等效公式的正确性以及座椅-座椅悬架-人体耦合模型等效为两自由度弹簧质量系统的有效性。

3 座椅悬架的结构参数对等效刚度、等效阻尼和座椅-座椅悬架-人体系统传递特性的影响

由式(15)和(26)可知，弹簧的倾角，阻尼器的倾角，以及连杆长度和倾角都会影响系统的等效刚度和等效阻尼，从而影响系统的传递函数。下面分别讨论弹簧倾角，阻尼器倾角，连杆长度和倾角对系统传递函数的影响。

3.1 弹簧倾角

汽车座椅-座椅悬架-人体耦合模型的固有频率一般在1～2 Hz范围，改变弹簧的倾角会影响悬架系统的等效刚度，该过程中在原来弹簧角度φ的基础上减少和增加5°以保持系统固有频率基本不变。由式(15)计算可得：弹簧倾角发生变化时悬架结构的等效弹簧力和等效刚度变化如图8所示；由式(29)得到系统传递函数峰值频率与幅值对比以及由式(27)相对阻尼系数对比见表4。由图8中可知，弹簧倾角的变化影响系统的等效刚度以及共振峰的频率和幅值，弹簧角度减小时，悬架结构等效刚度变小，弹簧刚度在悬架行程中的变化更为缓慢，即降低座椅悬架在拉伸段撞击到限位块的概率，共振峰的频率和幅值均有所减小；弹簧角度增加时，悬架结构等效刚度变大，弹簧刚度在悬架行程中的变化更为加快，座椅悬架在拉伸段撞击到限位块引起冲击的现象更容易发生，共振峰的频率和幅值均有所增加。

图8 不同弹簧倾角时悬架结构的等效弹簧力和等效刚度Fig.8 The effective spring force and stiffness of different spring angle

弹簧倾角传递函数Z1/Z0峰值频率/Hz峰值幅值传递函数Z2/Z0峰值频率/Hz峰值幅值相对阻尼系数初始角度1.071.571.131.780.24弹簧倾角增加5°1.121.621.181.870.237弹簧倾角减小5°1.031.51.051.660.25

3.2 阻尼器倾角

阻尼器的倾角会改变座椅悬架结构的等效阻尼，从而影响系统的传递函数。将阻尼器的角度在原来位置的基础上减少和增加5°，传递函数峰值频率与幅值以及相对阻尼系数对比见表5。阻尼倾角减小5°时，等效阻尼减小，系统传递函数在共振区的幅值增大；当阻尼倾角增加5°时，等效阻尼增大，系统传递函数在共振区的幅值减小。

表5 不同阻尼倾角时传递函数峰值频率和幅值对比

3.3 连杆长度和倾角

座椅实际结构中连杆是等长且关于交叉支点对称分布，由于驾驶室内空间位置的限制，在不改变座椅高度的情况下，按图9所示分别改变连杆点A、B和点C、D的位置，各点偏移距离均为20 mm，如位置1和位置2 所示，弹簧和阻尼器的位置保持原来位置不变。

图9 改变连杆长度和倾角示意图Fig.9 The different linkage position

连杆的长度和倾角的变化会导致等效刚度，等效阻尼的不同，从而影响系统的传递函数。由式(15)和(26)计算可得：连杆在位置1时，悬架结构的刚度减小，阻尼稍有增大；连杆在位置2时，悬架结构的刚度增大，阻尼增大，图10所示为连杆位置和倾角改变时悬架结构等效弹簧力和等效刚度的变化曲线，位置1时弹簧刚度在悬架行程中的变化更为缓慢，即减少座椅悬架在拉伸段撞击到限位块引起冲击的现象，位置2时弹簧刚度在悬架行程中的变化更为加快，座椅悬架在拉伸段撞击到限位块引起冲击的现象更容易发生。系统传递函数峰值频率与幅值对比以及相对阻尼系数对比见表6。

图10 连杆长度和倾角变化时的等效弹簧力和等效刚度Fig.10 The effective spring force and stiffness of different linkage position

连杆位置传递函数Z1/Z0峰值频率/Hz峰值幅值传递函数Z2/Z0峰值频率/Hz峰值幅值相对阻尼系数初始位置1.071.571.131.780.24连杆位置11.021.541.061.660.26连杆位置21.21.671.241.850.23

4 结 论

(1) 本文推导了剪式座椅悬架结构的等效弹簧力和等效阻尼力，得到等效刚度和等效阻尼，并将座椅-座椅悬架-人体耦合模型等效为二自由度弹簧质量系统，推导了该系统的传递函数；用Adams/view建立了座椅人体耦合模型来仿真实际的运动情况，并用Vibration模块进行分析得到系统的传递函数，将两种方法的到的结果对比，验证了理论推导的有效性。

(2) 本文分析了座椅悬架结构参数对座椅-座椅悬架-人体系统响应的影响，分别讨论了不同弹簧倾角、不同阻尼器倾角，以及不同连杆的长度和倾角对系统等效刚度及传递函数的影响。计算结果表明：弹簧倾角越小，等效刚度越小，在整个座椅行程中变化趋势较为平缓，减小座椅悬架在拉伸段撞击到限位块的现象的发生，共振峰的频率和幅值均有所减小。阻尼倾角减小时，等效阻尼减小，系统传递函数在共振区的幅值增大；当阻尼倾角增加时，情况相反。而连杆的长度和倾角的变化会同时影响悬架结构的等效刚度和等效阻尼，连杆长度减小倾角增大时，等效刚度越小，在整个座椅行程中变化趋势较为平缓，减小座椅悬架在拉伸段撞击到限位块并引起冲击的现象的发生，等效阻尼减小，系统传递函数固有频率和共振区的幅值减小。悬架结构影响的变化规律为进行座椅结构的优化设计提供参考。

[1] HUANG Xiaoxi, RAKHEJA S. Performance analysis of a relative motion based magneto-rheological damper controller for suspension seats[C]//ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference,2010,4:39-48.

[2] SHAHZAD F, QIU Y. A nonliear multi-body dynamic model of a suspension seat with occupant correlated with experimental results[C]//Presented at the 47th United Kingdom Conference on Human Responses to Vibration,2012.

[3] INENDINO L V, STRAUSS M G, MEDANIC J V. Development of a dynamic model of an air-ride seat for on highway trucks[C]/SAE paper,2003.

[4] KIM T H, KIM Y T, YOON Y S. Development of a biomechanical model of the human body in a sitting posture with vibration transmissibility in the vertical direction[J]. International Journal of Industrial Ergonomics, 2005,35(9):817-829.

[5] 朱思洪, 王家胜, 王敏娜. 带附加气室空气悬架剪式座椅振动特性试验研究[J]. 振动与冲击,2009，28(11):104-106.

ZHU Sihong, WANG Jiasheng, WANG Minna. Experimental study on vibration characteristics of scissors linkage seat with air suspension attached with auxiliary chamber[J]. Journal of Vibration and Shock, 2009，28(11): 104-106.

[6] 朱思洪, 朱星星, 马然,等. 驾驶员座椅半主动空气悬架系统振动特性实验研究[J]. 振动与冲击,2013，32(15):168-172.

ZHU Sihong, ZHU Xingxing, MA Ran. Vibration characteristics of the semi-active air suspension system of driver seat[J]. Journal of Vibration and Shock, 2013，32(15):168-172.

[7] MCMANUS S J, ST CLAIR K A, BOILEAU P É, et al. Evaluation of vibration and shock attenuation performance of a suspension seat with a semi-active magnetorheological fluid damper[J]. Journal of Sound and Vibration,2002,253(1):313-327.

[8] DUKE M, GOSS G. Investigation of tractor driver seat performance with non-linear stiffness and on-off damper[J]. Biosystems Engineering,2007,96(4):477-486.

[9] BOILEAU P É, RAKHEJA S, WANG Z, et al.Performance analysis of suspension seats under high magnitude vibration excitations part 1 model development and validation[J]. Journal of Low Frequency Noise, Vibration and Active Control,2003,22(4):225-252.

[10] 王岩松, 何辉, 耿艾莉. 车辆-人体系统振动时域模拟及悬架非线性分析[J]. 振动与冲击,2007,26(12):36-39,69-70.

WANG Yansong, HE Hui, GENG Aili. Time-domain simulation of vehicle-human vibration system and analysis of nonlinear susoension[J]. Journal of Vibration and Shock, 2007，26(12):36-39,69-70.

[11] KUMBHAR P B, XU Peijun, YANG Jingzhou. A literature of biodynamic models for whole body vibration and vehicle ride comfort[C]//ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference,2012.

[12] BOILEAU P É, RAKHEJA S. Whole-body vertical biodynamic response characteristics of the seated vehicle driver:Measurement and model development[J]. International Journal of Industrial Ergonomics,1998，22(6):449-472.

Calculation and analysis for equivalent stiffness and damping of a scissor type seat-seat suspension-human body system

SHUI Yijie, RAKHEJA Subhash, SHANGGUAN Wenbin

(School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510641, China)

A coupled dynamic model with 2-DOF for a seat-seat suspension-human body system was built, the equivalent stiffness and equivalent damping of the system were defined, and the formulas to calculate them were developed and presented. The transfer functions of the system were derived. Based on the developed model and the calculation formulas, the effects of linkage sizes of seat suspension, locations of spring and damper on the equivant stiffness, the equivaleat damping, and the transfer functions of the system were analyzed. The developed model provided an analysis model for optimizing the stiffness and damping, and transfer functions of scissor type seat-seat suspension-human body systems.

seat-seat suspension-human body system; equivalent stiffness; equivalent damping rate; transfer function

国家自然科学基金(51475171);广东省自然科学基金(6140310)

2015-08-13 修改稿收到日期：2015-10-08

水奕洁 男，女，硕士生，1992年生

上官文斌 男，博士，教授，1963年生

TH113.2+2

A

10.13465/j.cnki.jvs.2016.19.007