碾压砼重力坝深层抗滑稳定问题探讨

杨启龙

（水利部新疆水利水电勘测设计研究院,新疆 乌鲁木齐 830000）

1 引言

碾压砼重力坝深层软弱结构面是大坝设计中经常遇到的工程地质问题,沿软弱结构面的坝体抗滑稳定是保证大坝结构稳定的关键。在抗滑稳定分析方法中,刚体极限平衡法应用较为广泛,其主要包括被动抗力法和等安全系数法,后者要求滑动体和抗力体所具备的抗滑稳定安全系数必须相等,且均在2.3 以上。结合水利大坝运行实际,滑动体和抗力体相互依存,抗滑稳定安全系数理应相等,所以等安全系数法抗滑稳定分析方法更为合理。在应用等安全系数法进行碾压砼重力坝深层抗滑稳定分析的过程中必须合理选取抗力角和抗力体底滑面,保证分析结果的科学合理性及可靠性。

2 工程概况

水利枢纽工程位于新疆北疆地区,距乌鲁木齐约528.5 km。大坝基岩上层为K1c2-1岩屑石英砂岩,下伏K1c1黏土岩。河床段坝基岩屑石英砂岩由上至下依次为连续的缓倾角软弱夹层,编号NS2-1-9、NS2-1-8、JS2-1-2,对应倾角为3.25°、3.10°、1.34°,以上软弱夹层均未露头,部分剪断基岩在坝体带动下将沿潜在滑裂面滑动。设计时为保证深层抗滑稳定,坝基和消力池底板均封闭抽排,并在坝踵基岩内增设混凝土齿槽。本文主要进行水利枢纽工程表孔坝段深层抗滑稳定分析,并论证碾压砼重力坝深层抗滑稳定性,所使用到的物理力学参数见表1。

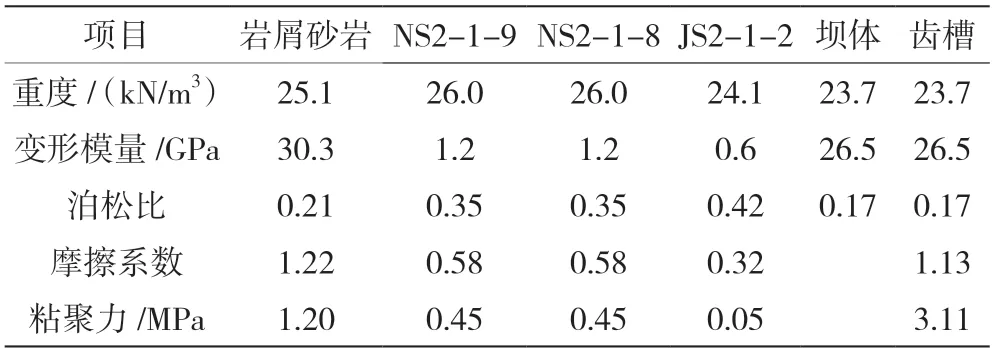
表1 碾压砼重力坝物理力学参数

3 抗力角γ 的合理选取

坝基内重力坝缓倾角软弱结构面深层滑动通常表现为双斜滑动面型式,其滑动体与抗力体受力情况见图1。根据抗剪断强度公式,滑动体及受其带动的部分岩体极限平衡方程式和抗力体极限平衡方程式表示如下：

图1 滑动体和抗力体受力情况示意图

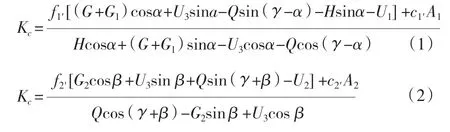
根据（2）式可推导出抗力的表达公式：

式中：G 为坝体上所作用的全部荷载的垂直分值,kN；G1为坝基软弱层之上地基结构自重；G2为抗力体结构自重,kg；H为坝体上所作用的全部荷载水平分值,kN；Q 为抗力体所具备的抗力,MPa；U1为1#滑裂面扬压力,kN；U2为2#滑裂面扬压力,kN；U3为3#滑裂面扬压力,kN；α为软弱层和水平面夹角,（°）；β为抗力体底滑面BC 和水平面夹角,（°）,即滑出角；γ为抗力体所具备抗力Q 和水平面的夹角,（°）,即抗力角；f 为摩擦系数；KC为抗滑稳定安全系数；c 为滑动面粘结力,kN；A 为测压系数。

图1 中AA'为坝基岩体上游端拉裂面,仅作为安全储备,不计算其抗拉作用；BC 为底滑面；BD 为假定的滑裂面。由于AA'位于帷幕前,应根据静水头将水压力延伸至A'处。水利枢纽大坝地震惯性力按照7 度地震及正常蓄水位下各阶沿河向振型惯性力平方和的二次开方确定[1]。滑动面以上的岩体惯性力则根据水工建筑物抗震设计规范相关要求确定。被齿槽所切断的坝体软弱夹层抗剪强度参数均通过面积加权平均计算。

根据式（3）可以看出,抗力随抗力角的增大而增大,也说明坝基深层抗滑稳定安全系数较大,所以,只有保证抗力角取值的合理性,才能获得可靠的深层抗滑稳定计算结果。根据相关研究成果,工程碾压砼重力坝深层抗滑稳定破坏试验中抗力角可以取0°、α、tan-1（f/k）及BD 面主应力方向和水平面夹角值（即γ=0°、γ=α、γ=15°、γ=20°）。具体而言,应采用等安全系数法并依据抗力公式进行沿NS2-1-9、NS2-1-8、JS2-1-2 潜在滑动面抗滑稳定性的计算,并研究抗力角的取值范围。沿NS2-1-9、NS2-1-8、JS2-1-2 潜在滑动面的抗滑稳定性计算结果具体见表2～表4。

表2 沿NS2-1-9 潜在滑动面的抗滑稳定性计算结果

表3 沿NS2-1-8 潜在滑动面的抗滑稳定性计算结果

表4 沿JS2-1-2 潜在滑动面的抗滑稳定性计算结果

由计算结果可以看出,抗力角γ从0°增大至20°,则沿NS2-1-9、NS2-1-8、JS2-1-2 潜在滑动面抗滑安全系数分别从2.56、2.31、1.98 增大至4.23、3.77、2.50,很明显,水利枢纽碾压砼重力坝深层抗滑稳定安全系数随抗力角γ的增大而呈增大趋势,并总能够选择一个抗力角γ,使其对应的安全系数符合规范。然而,针对工程实际,若深层抗滑稳定安全系数取值既定,则抗力角γ的取值也是确定的,超出其取值的安全系数则不可靠；若深层抗滑稳定安全系数取值不确定,则采用较大的抗力角γ得到的安全系数虽符合相关规范,但并不可靠[2]。可见,水利工程碾压砼重力坝抗力角γ的合理取值对于工程安全运行十分重要。根据重力坝设计规范,抗剪断强度公式在具体应用过程中,深层抗滑安全系数取值应不小于2.3,根据式（3）可知,抗力角γ=0°时所对应的抗力最小,且此种工况下沿NS2-1-9 潜在滑动面的抗滑安全系数远远大于2.3,沿NS2-1-8 潜在滑动面的抗滑安全系数也刚刚超出2.3,并且随着抗力角γ的增大而呈增大趋势,表明沿该水利枢纽碾压砼重力坝滑动面的抗滑稳定安全裕度较大。

通常对碾压砼重力坝进行基本荷载组合下数值分析,以论证抗力角γ取值的合理性[3],以所计算出的BD 面主应力方向和水平面夹角均值为抗力角γ的最大取值依据。对基本荷载组合下水利枢纽碾压砼重力坝表孔坝段进行三维有限元应力分析,所得到的BD 面主应力向和水平面夹角角度约为20°,且抗力角γ取20°时符合该水利枢纽碾压砼重力坝表孔坝段基本荷载组合下坝基岩体实际受力,该抗力角取值也较为可靠,其对应的是安全系数最大值。进行碾压砼重力坝深层抗滑稳定计算时,如果抗力角γ取0 得到的安全系数符合要求,则表明抗滑稳定处于安全状态；若安全系数不符合要求,并不意味着抗滑稳定不安全,此时可取抗力角γ=α,使抗力方向平行于主滑动面。根据表4 的计算结果也可以看出,当γ=α=1.34°则沿JS2-1-2 潜在滑动面的抗滑稳定安全系数并不满足要求,则必须通过模拟坝基软弱夹层从而进一步分析大坝及基础应力情况,以所确定出的BD 面主应力向和水平面夹角为抗力角γ的取值上限,进行抗滑稳定性能的判断。抗力角γ=20°时所对应的抗滑稳定安全系数取值2.50,满足抗滑稳定安全要求。

4 滑出角β的合理选取

抗力体底滑面与水平面夹角即为滑出角β,当以坝址下游基岩内破裂面为抗力体底滑裂面时,必须进行各个滑裂面抗滑稳定计算。然而,大多数基岩中并无抗力体底滑裂面,该滑裂面一般为假设存在,故所对应的滑出角β也属于假设存在。通常情况下,滑出角β取值越小,则抗力体越大,所对应抗力Q 值也越大,由此得到的抗滑稳定安全系数取值也越大。所以,必须合理确定滑出角β值,以保证碾压砼重力坝抗滑稳定安全系数取值的准确合理。当γ角确定时,可通过被动抗力法的最小抗力原则确定滑出角β值,即采用迭代法联立迭代求解式（1）和式（3）,在所得到的诸多滑出角β值中选择最小抗力Q 及所对应的抗滑安全稳定系数KC。此处仅分析沿NS2-1-8 潜在滑动面的抗滑稳定安全系数KC求解过程中,当抗力角γ=0°时,在所得到的滑出角β值中逐个试算,以得到最小抗力Q,并和式（1）迭代计算便可求得抗滑稳定安全系数KC及抗力值Q,结果见表5。

表5 沿NS2-1-8 潜在滑动面γ=0°时抗滑稳定计算结果

根据计算结果,滑出角β值越小,则抗力越大,所对应的碾压砼重力坝深层抗滑稳定安全系数也越大。当滑出角β取32.4°时,所对应的抗滑稳定安全系数KC及抗力值Q 均最小,此后随着滑出角β的增大,抗滑稳定安全系数KC及抗力值Q 均呈增大趋势。所以,滑出角β取32.4°是符合设计原则的极限值,其所对应的安全系数也比2.3 大,充分说明,沿NS2-1-8 潜在滑动面γ=0°时便达到抗滑稳定要求,且安全裕度较大。

5 结论

综上所述,通常采用抗剪断强度公式,并按双斜滑裂面刚体极限平衡等安全系数法进行碾压砼重力坝深层抗滑稳定分析,且抗力角γ取值与安全系数取值呈正向变动关系,主要通过数值分析法进行抗力角γ取值合理性的分析。当抗力角γ=0°时所计算得抗滑稳定安全系数取值符合规范,则表明重力坝抗滑稳定安全；若不符合规范,并不意味着抗滑稳定不安全,必须取抗力角γ=α再算；若仍不符合规范,则应应用数值分析法确定出BD 面主应力向和水平面夹角均值,以该角度值为抗力角上限再进行重力坝深层抗滑稳定分析；若抗滑稳定系数还不符合规范,则必须采取工程措施,提升水力枢纽工程碾压砼重力坝深层抗滑稳定性。水利枢纽沿NS2-1-9、NS2-1-8 潜在滑动面抗滑安全系数在抗力角γ=0°时分别为2.56、2.31,抗滑安全裕度较大；沿JS2-1-2 潜在滑动面抗滑安全系数在抗力角γ=15°时为2.41,在γ=20°时达到2.50,表明该碾压砼重力坝坝段深层抗滑稳定处于安全状态。