内爆炸载荷下双层钢管结构的动力响应
2016-11-23李世强王志华吴桂英
刘 珍, 李世强, 李 鑫, 王志华, 吴桂英
(1.太原理工大学 力学学院,太原 030024; 2.太原理工大学 应用力学与生物医学工程研究所,太原 030024)
内爆炸载荷下双层钢管结构的动力响应
刘 珍1, 李世强2, 李 鑫2, 王志华2, 吴桂英1
(1.太原理工大学 力学学院,太原 030024; 2.太原理工大学 应用力学与生物医学工程研究所,太原 030024)
采用实验与数值模拟相结合的方法研究了双层钢管结构在内爆炸载荷作用下的动力响应。考察了内外层钢管的壁厚设置与炸药质量对结构变形失效模式及其抗爆性能的影响。结果表明:与外管壁厚相比,内管壁厚对结构变形失效模式起主导作用,随着炸药质量的增加,内管壁厚对结构变形的影响逐渐减弱;并且内管壁厚的改变显著影响结构的能量分配机制,增加炸药质量时,外管能量耗散增幅大于内管。
双层钢管;内爆炸;有限元分析;抗爆性
单层或双层圆管结构,已广泛应用在能源、造船、化工、石油和机械等领域[1-3]。在受到冲击载荷作用后,常发生整体或局部的损伤导致结构失去安全性,研究其在爆炸等冲击载荷下的动力响应可以准确地描述结构在这类载荷下的力学行为,对预测结构变形特征、提高结构抗爆性能有重要工程应用价值。
RUSHTON等[4]通过分析钢管在高能炸药内爆炸载荷下的超压与环向应变,指出在相同的炸药质量下,与等效的球形装药相较,柱型装药作用下钢管会产生更大的塑性变形,随着装药长径比增加,爆炸超压峰值与冲量都明显增加;LANGDON等[5]实验研究了两种不同炸药位置(钢管中心处和距管自由端150 mm处)下,一端固支另一端自由放置的钢管结构在内爆炸载荷下的动态响应,并通过数值模拟方法深入分析了固支端对钢管内部爆炸冲击波传播以及钢管整体响应的影响,发现当炸药位于管中心处时,钢管径向挠度随炸药质量增长呈线性增长。纪冲等[1]对外接触爆炸作用下钢管的破坏效应进行研究,得到小质量炸药爆炸后,钢管仅产生凹坑、鼓包及层裂等破坏,而大质量炸药爆炸后,钢管发生了剪切破坏,爆炸碎片可击穿管壁。SIMANGUNSONG等[6]提出内爆炸作用下钢管结构的振动衰减与结构的应变增长有关,并提出根据圆管的半径和壁厚预测其所能承受的内爆炸载荷等级。
目前有关双层钢管结构的研究多集中在管道热传导方面[3,7],在天然气等可燃易爆气体的运输和储存的过程中及热能管道工程中难免因外界环境影响发生意外爆炸事故,但关于这种双层钢管结构在受到内爆炸冲击时的动力响应和抗冲击性能的研究鲜有报导。本文在单层钢管内爆炸动力响应相关文献的研究基础上,针对双层钢管结构在内部柱形TNT装药作用下的变形失效模式进行了实验研究。并通过LS-DYNA有限元程序对其动力响应过程进行分析,讨论了内外层钢管壁厚设置和炸药质量对结构变形失效模式及其抗爆性能的影响。
1 实验研究
1.1 实验设置
实验所用试件为由Q345钢质圆管组成的双层钢管结构,结构长L为380 mm,内层钢管与外层钢管的外管径分别为Øinner=76 mm和Øouter=101 mm。通过改变内外钢管的壁厚,得到三组试件,如表1所示。实验中,结构两端用细绳悬挂在空中,并在内层钢管与外层钢管间放置垫块确保两层钢管同轴放置。爆炸载荷由放置在结构几何中心处的10 g柱形(长径比为1∶1)TNT装药中心起爆产生,柱形装药平行于结构轴线放置,实验设置如图1所示。
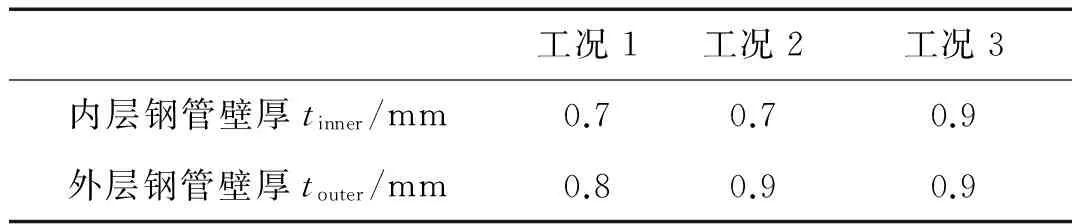
表1 实验工况
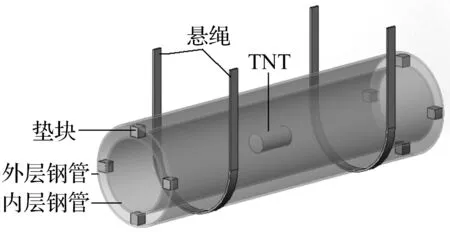
图1 实验装置图Fig.1 Schematic of experimental set-up
1.2 实验结果分析
三种工况下实验结果数据如表2所示,其中Lraise为外层钢管局部大变形区域在轴线方向的长度,D1为外层钢管在沿指向内管开裂方向上的径向变形后的长度,D2为外层钢管上与D1方向正交的径向变形后的长度,如图2所示。
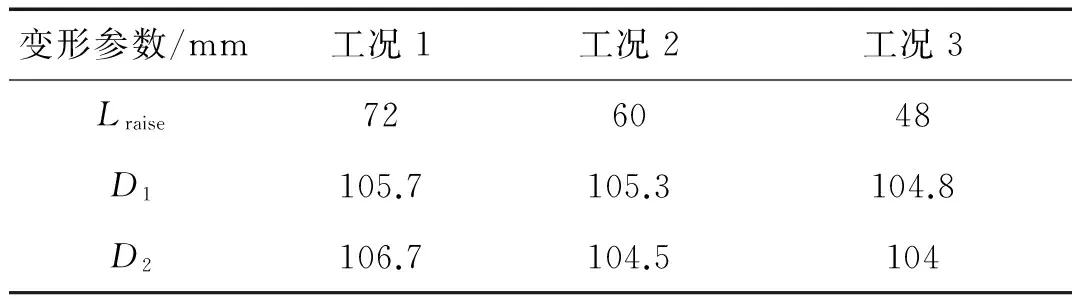
表2 双层钢管在内爆炸载荷下的变形结果

图2 实验变形参数示意图Fig.2 Schematic of the deformation parameter
图3给出结构在三种工况下的变形模态。从图3可以看出,在炸药位置处,内层钢管与外层钢管均发生隆起大变形;在远离炸药端,内外管均未表现出明显变形。因爆炸载荷的对称性,结构在轴向上的径向变形对称分布。靠近爆炸载荷位置处,内管发生较大径向膨胀,并在焊接处发生撕裂破坏,外层钢管同时受到膨胀后的内管撞击与内管撕裂处的爆炸冲击波作用,没有发生撕裂破坏。可以看到,在内层钢管发生撕裂的一侧,外层钢管的塑性变形明显大于另外一侧,这主要是由于内管的撕裂导致爆炸冲击波直接作用在外管壁上而形成的。实验中还发现:保持内管(外管)壁厚不变,随着外管(内管)壁厚的减小,外层钢管在内管撕裂处的隆起变形范围增大,且变形区域形状由矩形(正视)逐渐变成椭圆(正视)。

图3 双层钢管的变形模态Fig.3 Deformation modes of double-layersteel pipes
2 数值模拟
为进一步研究结构的变形失效特征,应用Ls-Dyna有限元程序对其在内部柱形TNT装药爆炸作用下的动力响应进行了数值模拟研究。模拟讨论中通过壁厚为0.7 mm、0.8 mm和0.9 mm的内层钢管(Øinner=76 mm)与外层钢管(Øouter=101 mm)排列组合将试件增加到9组进行研究。
2.1 有限元模型
TNT炸药的材料性能采用高能炸药模型模拟,通过JWL状态方程对其爆轰产物的膨胀规律进行描述。炸药爆轰产物压力与其体积膨胀的关系表示为[8]:
(1)
式中:p为爆压,ω、A、B、R1、R2为状态方程参数,E0为单位体积的炸药内能。数值计算中,炸药密度为1 630 kg/m3,爆轰速度为6 700 m/s,C-J爆轰压力为19 GPa。JWL状态方程参数[8]为:A=371 GPa,B=3.23 GPa,R1=4.15,R2=0.95,ω=0.3,E0=7.0 GJ/m3。
双层钢管结构采用塑性等向强化模型,该模型考虑了结构的大变形与材料的应变率效应。其中,应变率效应由Cowper-Symonds模型给出。钢管材料密度为7.83 kg/m-3,弹性模量为201 GPa,屈服强度为345 MPa,泊松比为0.3。应变率参数C与P分别取40 s-1与5[9]。
模拟中TNT炸药采用SOLID 164六面体ALE实体单元;结构采用SHELL 163四边形Lagrange壳单元。经过网格敏感性验证,钢管结构单元边长为2 mm,外层钢管共有30 560个节点,30 400个单元,内层钢管共有23 493个节点,22 990单元。有限元网格模型如图4所示。为了便于观察,图4中只显示了1/2有限元计算模型。
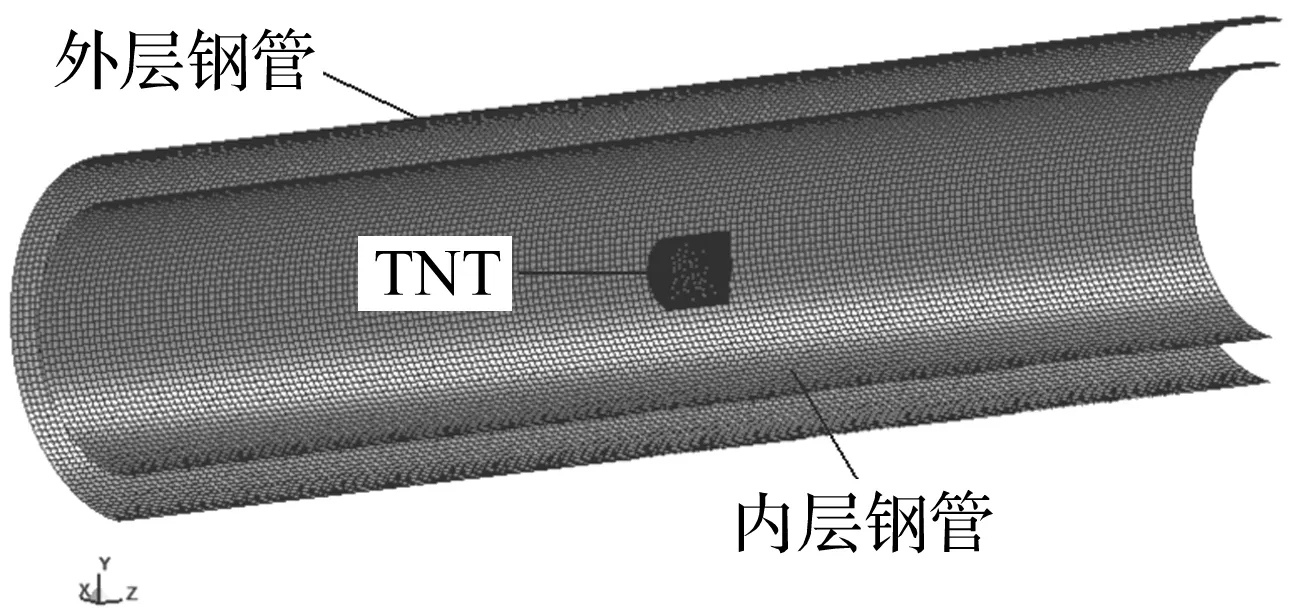
图4 有限元计算模型Fig.4 The finite element model
实验中双层钢管结构通过细绳自由悬于空中,所用细绳为布丝带,悬于结构两端(见图1),忽略其对结构变形的约束作用,因此,数值模拟中设置结构为自由边界。TNT炸药在结构几何中心处起爆,产生的爆轰产物与结构的变形响应发生耦合,造成结构的大变形,炸药与内层钢管间采用侵蚀面对面接触算法。内管和外层钢管间定义自动面对面接触。
2.2 模型验证
为验证有限元计算模型的可靠性,分别从双层钢管结构的最终变形模态、外层钢管变形参数(Lraise、D1以及D2)与实验数据进行了比较。考虑到实验中内层钢管在载荷作用处发生焊接撕裂破坏,通过材料赋值法[10]建立高组配焊接单元[11]模型模拟内管的撕裂破坏。
图5对比了实验与数值模拟下双层钢管结构(工况1)的变形模态,可以看出:结构在内部柱形TNT炸药爆炸作用下发生局部大变形,内层钢管向外膨胀,并在焊接处发生撕裂破坏。在内管撕裂处,外层钢管呈现大范围矩形隆起变形。有限元计算结果与实验模态吻合较好。

图5 双层钢管变形模态数值模拟与实验对比Fig.5 Numerical deformation of double-layer steel pipes compared with experimental deformation
图6(a)给出了双层钢管结构(工况1)典型的能量历史,图6(a)表明体系中所产生的沙漏能占总能量的4.89%,在工程上是可行的。图6(b)给出了3种工况下外层钢管变形参数实验结果(Lraise、D1以及D2)与数值模拟结果对比。外管变形参数Lraise、D1以及D2数值模拟结果与实验测量结果误差分别为1.6%、0.7%和0.1%,可以看出数值计算结果与实验结果吻合较好。因此,本文建立的有限元模型是可靠的,可以用来研究双层钢管结构的抗爆性能。
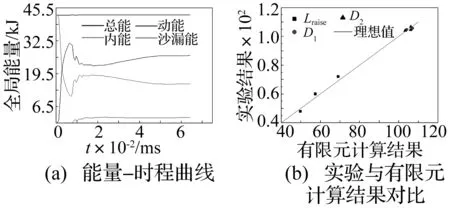
图6 双层钢管有限元模型验证Fig.6 Validation of FE model of double-layer steel pipes
3 数值计算结果与分析
实验中内爆炸载荷作用下双层钢管结构的内层钢管均发生撕裂破坏,但内管焊接失效及其产生的影响并不是本文研究重点,下述研究内爆炸载荷下双层钢管结构的整体动力响应,为简化分析,以下数值模拟不考虑内管由于焊缝引起的撕裂破坏。
3.1 炸药与双层钢管响应过程
图7给出了结构在内部10 gTNT柱状装药爆炸作用下典型的压力时程曲线。可以看出,炸药与结构的动力响应过程分为三个阶段:阶段Ⅰ(0~7 μs),炸药起爆到与结构相互作用;阶段Ⅱ(8-41μs),炸药热膨胀产物与结构的耦合作用;阶段Ⅲ(42~1 000 μs),惯性作用下结构的变形。图8给出了炸药爆轰膨胀产物与结构发生相互作用的典型过程。
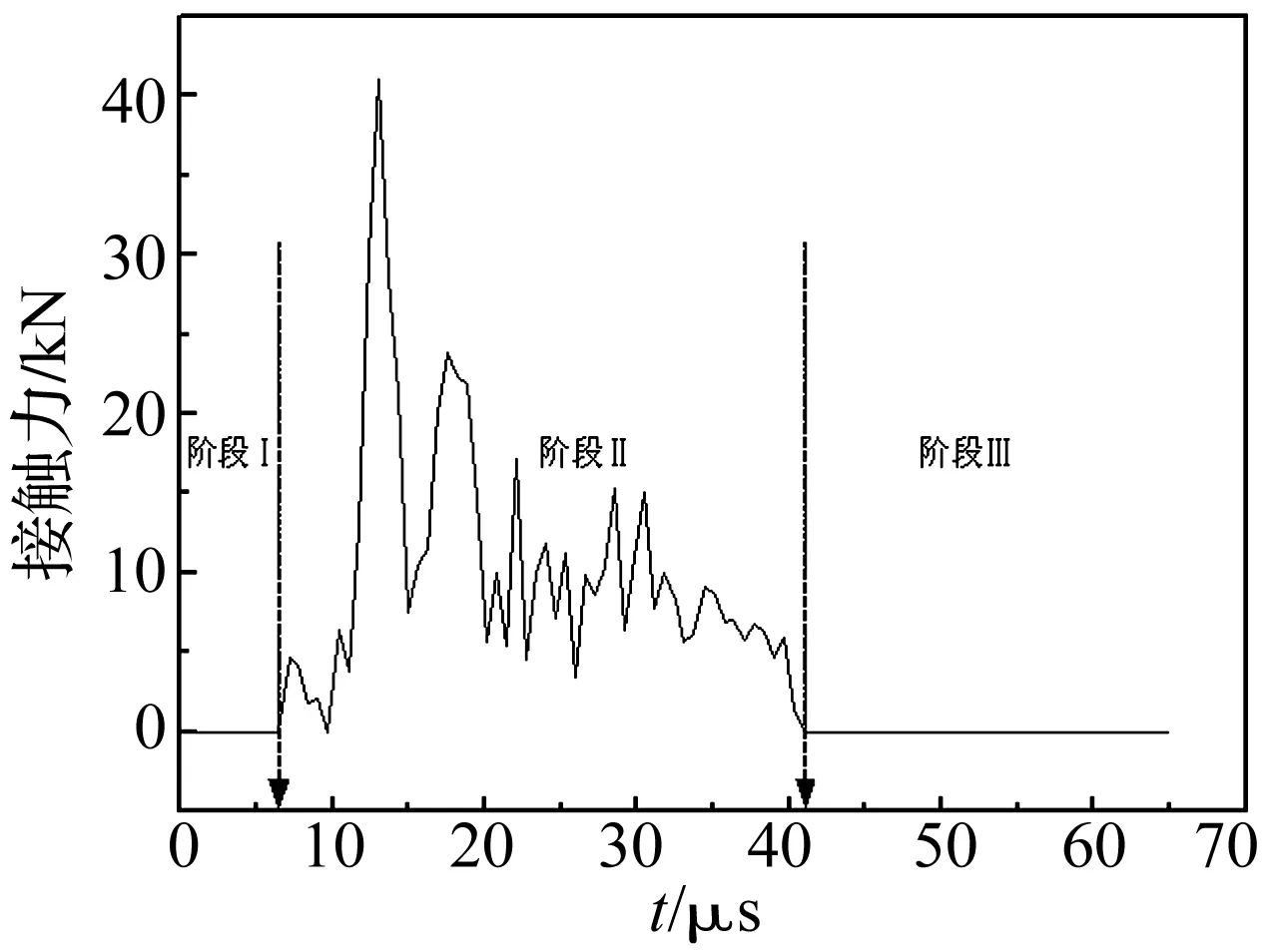
图7 典型压力-时程曲线(touter=0.8 mm,tinner=0.7 mm)Fig.7 Typical pressure-time curve (touter=0.8 mm, tinner=0.7 mm)
阶段Ⅰ:从图8(t=0~40 μs)可以看出,炸药从中心起爆点开始向外膨胀,由于双层钢管结构的约束作用,爆轰产物径向的传播速度远小于轴向的传播速度。
阶段Ⅱ:爆轰波开始作用在双层钢管结构上,爆炸产物与结构发生相互作用,接触力瞬间达到41 kN,然后迅速衰减直至减小到0,作用时间持续约33 μs。爆轰波作用在结构的内层钢管后,内管中心区域出现沿径向外的膨胀变形,并随着能量的传递沿轴向向外扩展,此时,外层钢管变形很小。当接触力等于零时(t=41 μs),耦合作用完成,删除炸药模型。
阶段Ⅲ:删除炸药后,结构继续在惯性作用下变形,如图8(t=42 μs ~500 μs)。结构的变形从结构中部向外扩展,当变形扩展到端部时,外层钢管发生明显变形,结构呈现整体的膨胀变形模式。

图8 双层钢管的变形过程(touter=0.8 mm,tinner=0.7 mm)Fig.8 Deformation of double-layer steel pipes (touter=0.8 mm,tinner=0.7 mm)
3.2 双层钢管的变形
图9给出了结构内层钢管中心处的径向速度及两层钢管间的压力时程曲线。可以看出,在炸药产物与结构响应过程中,结构中部受到爆炸冲击波作用,内管中心处径向速度瞬时增至397 m/s,然后迅速降低。随后,外管与内管开始接触,并获得一定初始速度,相同地,外管中心处速度在瞬时达到峰值后迅速降低。
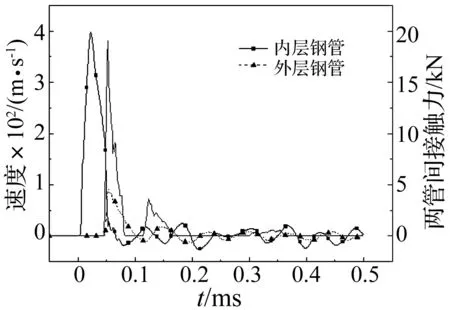
图9 双层钢管中心处速度-时程曲线和两层钢管间接触力曲线(touter=0.8 mm,tinner=0.7 mm)Fig.9 Velocity-time curves on the charge position and contact force between two pipes (touter=0.8 mm,tinner=0.7 mm)
双层钢管结构为空气夹芯结构,在内部平行于管轴线放置的10 g柱形TNT炸药爆炸冲击下,管中部发生局部大变形,管端无明显的变形发生。内层钢管作为主要吸能构件[12],吸收了95.3%的能量,产生明显的局部大变形。外层钢管在残余能量作用下,管中部也发生膨胀变形。图10给出了内外钢管典型的位移-时程曲线。内管在7 μs开始变形,挠度持续增加,直至达到最大挠度12.2 mm,外管滞后内管40 μs开始变形。
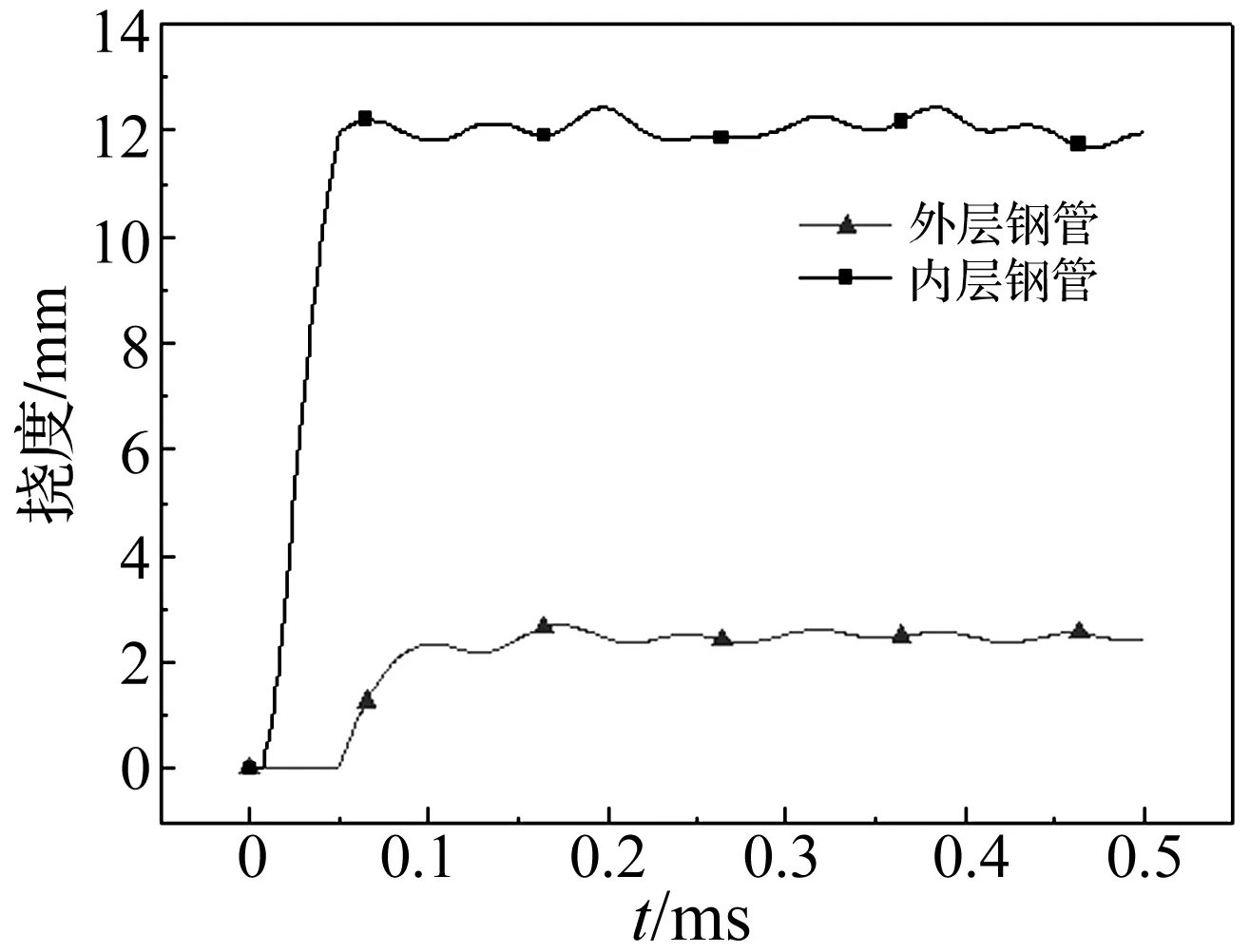
图10 双层钢管中心处位移-时程曲线(touter=0.8 mm,tinner=0.7 mm)Fig.10 Deflection-time curves of double-layer steel pipes on the charge position (touter=0.8 mm,tinner=0.7 mm)
3.3 双层钢管抗爆炸冲击性能
3.3.1 外层钢管挠度
图11中给出了10 gTNT爆炸作用下,9组双层钢管结构在外管中心处的径向挠度。可以看出,与增大外层钢管壁厚touter相比,增加内层钢管壁厚tinner时外管中部挠度的降低更为显著。例如,当touter=0.7 mm时,tinner从0.7 mm增至0.8 mm时,外管挠度减小78.6%,而当tinner=0.7 mm,touter从0.7 mm增至0.8 mm时,外管挠度仅减小6%。当内管壁厚增至0.9 mm时,外管均未产生径向挠度,这是由于内管壁厚为0.9 mm时,10 g炸药爆炸作用下内管的径向挠度小于双层钢管间的间隙,外管不受内管的挤压,因此未发生变形。
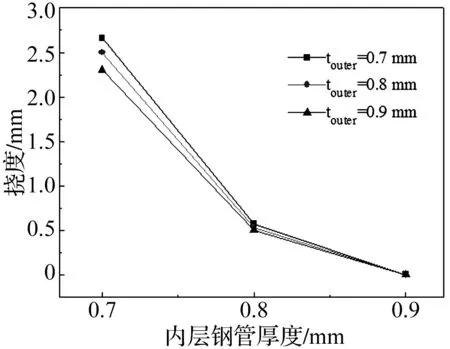
图11 不同壁厚设置下外层钢管中心处挠度Fig.11 Deflection of out tube on the charge position
图12给出了外管壁厚为0.7 mm,内管壁厚度从0.7 mm增至0.8 mm时和内管壁后为0.7 mm,外管壁厚度从0.7 mm增至0.8 mm时的外层钢管中部挠度的减小量随炸药质量的变化情况。从图12可以看出,在较小质量炸药(<15g)爆炸作用时,当外管壁厚为0.7 mm,內管壁厚从0.7 mm增至0.8 mm时,外管挠度的减小量很可观。但当炸药质量增加至15 g时,外管挠度的减小量降为21.4%,较10 g炸药爆炸作用下降低了72.8%。且随着炸药质量继续增加,外管挠度的减小量缓慢降低。还可以看到,当内管壁厚为0.7 mm,增加外管壁厚度时,外管挠度的减小量变化随着炸药质量的增加较平缓,保持在6%左右。
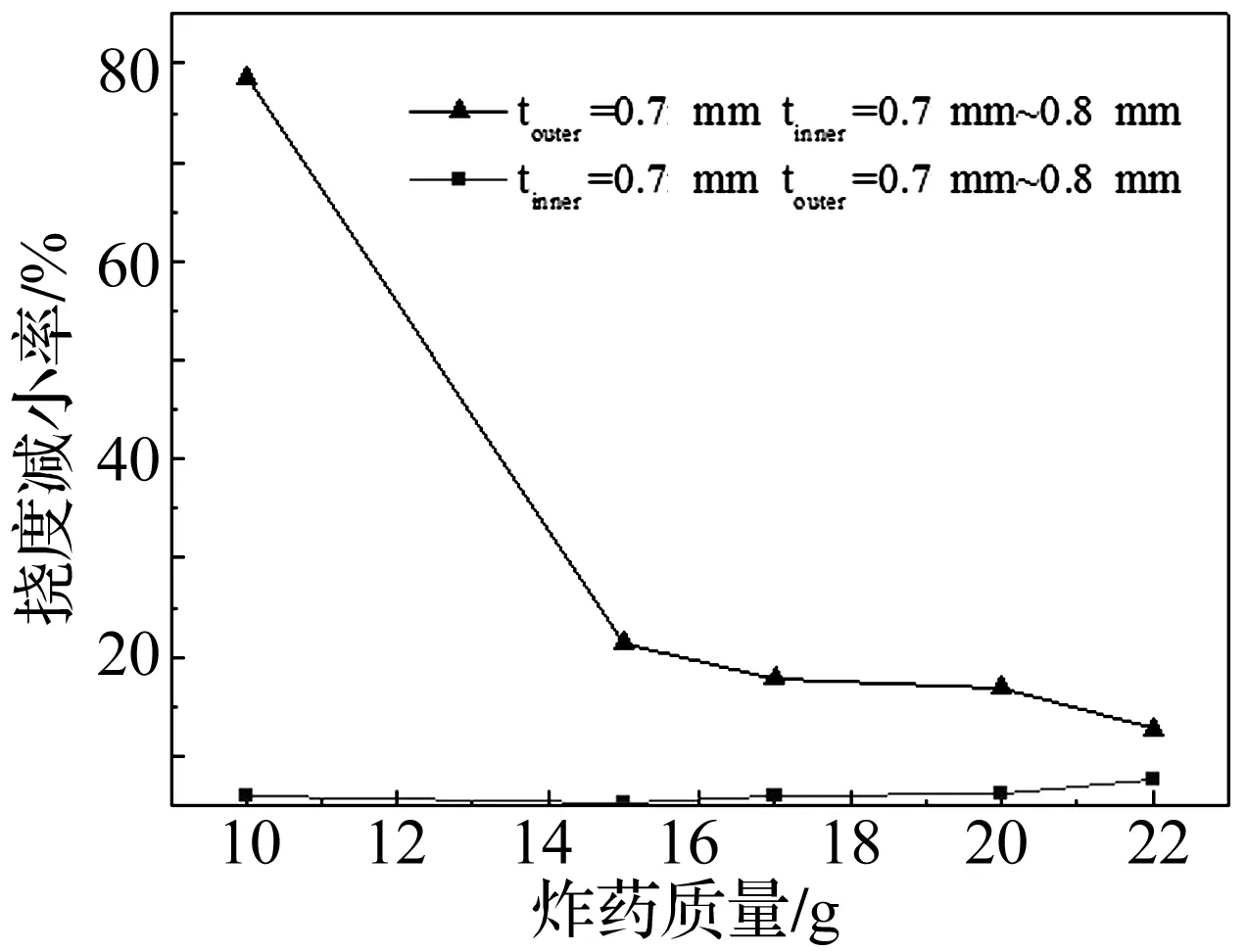
图12 不同炸药质量下外层钢管中心处挠度的减小量Fig.12 Reduction of deflection on the charge position under different charge masses
3.3.2 双层钢管的能量吸收
双层钢管结构的抗爆性能与其能量吸收也密切相关。通过对数值模拟中9组试件在10 gTNT炸药爆炸作用下各部分(内层钢管与外层钢管)能量分析,图13给出了9组试件在10 gTNT炸药爆炸下结构各部分的能量吸收结果。可以看出外管壁厚度一定下,随着内管壁厚的增加,结构质量增加,刚度变大,结构的变形相应的减小,内外管吸收的能量也降低。但当内管壁厚度一定时,外管壁厚的增加对结构能量吸收机制没有明显的影响,这是由于结构受到爆炸载荷冲击后,内管受到直接作用,吸收95%以上的能量。
随着炸药质量的增加,作用于结构的爆炸冲击载荷也增加,结构内外管吸收的能量不断增大,进而产生更大的塑性变形。从图14可以看出,对于外管壁厚touter=0.8、内管壁厚tinner=0.7的双层钢管结构,在炸药内爆炸作用下,內层钢管的能量吸收均大于外层钢管,这种现象在炸药质量为10 g时尤为明显。当炸药质量为15 g时,内外层钢管的能量吸收幅度均迅速增大,且内管的能量吸收明显多于外管。但随着炸药质量继续增加,外层钢管能量吸收幅度逐渐大于内层钢管。这是因为随着炸药质量的增加,外层钢管的变形逐渐增大,而内层钢管的变形受到外层钢管的约束,其塑性能耗散量增幅减缓,外层钢管的塑性能量耗散逐渐增加。
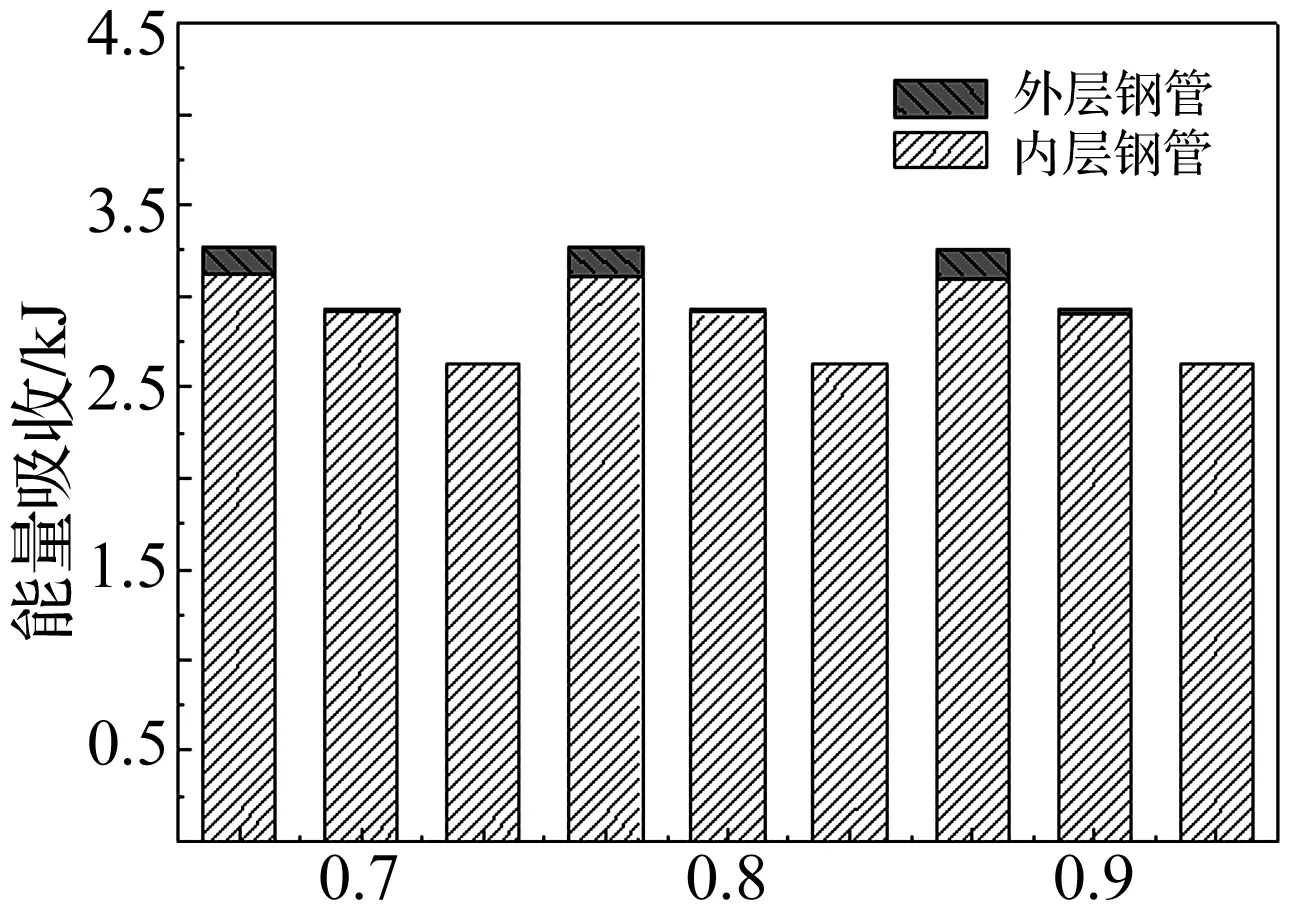
图13 双层钢管的能量吸收Fig.13 Energy absorption of different double-layer steel pipes
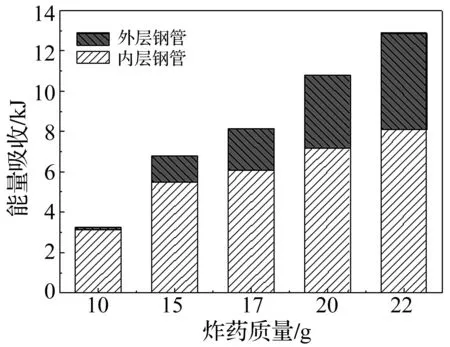
图14 不同炸药质量下能量吸收(touter=0.8 mm,tinner=0.7 mm)Fig.14 Energy absorption under different charge masses (touter=0.8 mm,tinner=0.7 mm)
4 结 论
针对双层钢管结构在内部柱形TNT炸药爆炸作用下的动力响应开展了实验和数值模拟研究。在本文研究范围内可得到以下结果:
(1) 内层钢管的开裂失效显著改变了双层钢管结构的变形失效模态。保持内管(外管)壁厚不变,随着外管(内管)壁厚的减小,外层钢管在内管撕裂处的隆起变形范围增大,且变形区域形状由矩形逐渐变成椭圆形。
(2) 与外层钢管壁厚相比,内管壁厚对双层钢管结构的变形模式起主导作用,随着炸药质量增加,内管壁厚对结构变形模式的影响逐渐减弱。
(3) 内层钢管壁厚的改变对结构的能量吸收有着显著影响。增加炸药质量,内管的能量耗散增幅逐渐减小,然而外管能量耗散增幅却随着炸药质量增加逐渐加大。
[1] 纪冲,龙源,方向,等.外接触爆炸荷载作用下大口径钢管变形与破坏效应的数值模拟[J].振动与冲击,2012,31(16):72-76.
JI Chong,LONG Yuan,FANG Xiang,et al. Numerical simulation of large-aperture steel pipe subjected to contact explosion loading [J]. Journal of Vibration and Shock, 2012,31(16):72-76.
[2] 顾建忠.国外双层金属复合钢管的用途及生产方法[J].上海金属,2000, 22(4):16-24.
GU Jianzhong. Use and production method of bimetallic clad steel tubes overseas [J]. Shanghai Metals, 2000,22(4):16-24.
[3] WRIGHT H, ODUYEMI T, EVANS H R. The experimental behavior of double skin composite element [J]. Journal of Constructional Steel Research, 1991, 19: 91-110.
[4] RUSHTON N, SCHLEYER G K, CLAYTON A M, et al. Internal explosive loading of steel pipes [J]. Thin-Walled Structures, 2008, 46(7/8/9): 870-877.
[5] LANGDON G S, OZINSKY A, YUEN S K. The response of partially confined right circular stainless steel cylinders to internal air-blast loading [J]. International Journal of Impact Engineering, 2014, 73: 1-14.
[6] SIMANGUNSONG G M, KUBOTAS, SABURI T. Dynamic response of a steel pipe to internal blast loading[J]. Materials Science Forum, 2008, 566: 29-34.
[7] YI H K, KIM E H, PARK S P, et al. Reliability analysis of stainless steel/carbon steel double-layered tube on the basis of thermal deformation behavior [J]. Journal of Mechanical Science and Technology, 2013, 27 (5): 1279-1285.
[8] JING L, WANG Z, ZHAO L. Dynamic response of cylindrical sandwich shells with metallic foam cores under blast loading—Numerical simulations [J]. Composite Structures, 2013, 99: 213-223.
[9] 余同希,邱信明.冲击动力学[M].北京:清华大学出版社,2011:65.
[10] 黄雪峰,樊壮卿,王伟力,等.基于LS-DYNA对于舰艇舱室焊缝模拟方法[J].海军航空工程学院学报,2014, 29(4):365-368.
HUANG Xuefeng, FAN Zhuangqing,WANG Weili, et al. Simulation method of ship cabin weld based on LS-DYNA [J]. Journal of Naval Aeronautical and Astronautical University, 2014, 29(4): 365-368.
[11] 王振家,陈伯蠡,弋成东.为较高强度的结构钢选择焊接材料须考虑的两个因素[J].热加工工艺,2004(8):47-48.
WANG Zhenjia, CHEN Boli, YI Chengdong. Two factors about selecting welding material for HSLA steel [J]. Hot Working Technology, 2004(8): 47-48.
[12] YAHAY M A, RUAN D, LU G, et al. Response of aluminium honeycomb sandwich panels subjected to foam projectile impact-An experimental study[J]. International Journal of Impact Engineering, 2015, 75: 100-109.
Dynamic responses of double-layer steel pipes under internal blast loading
LIU Zhen1, LI Shiqiang2, LI Xin2, WANG Zhihua2, WU Guiying1
(1. Mechanics College, Taiyuan University of Technology, Taiyuan 030024, China;2. Institute of Applied Mechanics and Biomedical Engineering, Taiyuan University of Technology, Taiyuan 030024, China)
The dynamic responses of double-layer steel pipes to internal blast loading were investigated using the method of tests combined with numerical simulation. Both effects of wall-thickness-arrangements of double-layer steel pipes and mass change of TNT charges on the failure mode of structural deformation and the pipers’ anti-blast performances were analyzed. The results indicated that compared to the change of outer pipe thickness, inner pipe thickness change this effect reduces with increase in charge mass; meanwhile, inner pipe thickness change affects obviously the structural energy distribution, energy dissipation in outer pipe increases faster than that in inner pipe does with increase in charge mass.
double-layer pipes; internal blast; FEA; blast resistance
国家自然科学基金项目(1172196;11402163);山西省自然科学基金项目(2014011009-1)
2015-05-18 修改稿收到日期:2015-10-08
刘珍 女,硕士,1989年生
吴桂英 女,教授,博士生导师,1962年生
O38
A
10.13465/j.cnki.jvs.2016.19.012
