考虑电机控制策略影响的电动车动力总成振动分析
2016-11-23于蓬,章桐,余瑶,郭荣
于 蓬, 章 桐, 余 瑶, 郭 荣
(1.同济大学 新能源汽车工程中心,上海 201804; 2.同济大学 汽车学院,上海 201804; 3.同济大学 中德学院,上海 201804)
考虑电机控制策略影响的电动车动力总成振动分析
于 蓬1,2, 章 桐1,2,3, 余 瑶1,2, 郭 荣1,2
(1.同济大学 新能源汽车工程中心,上海 201804; 2.同济大学 汽车学院,上海 201804; 3.同济大学 中德学院,上海 201804)
针对电动车动力总成存在的结构振动问题,提出机-电-磁-控一体的仿真方法,并在此基础上进行控制策略优化。首先,搭建综合考虑电机控制策略、电机电磁作用及详细机械结构的动力总成模型,体现所研究对象机电一体化的特点;然后进行电机电流、电磁力及总成振动响应的仿真与试验,验证所提多物理场仿真方法的正确性;最后从控制策略优化角度,而非机械结构改变角度,对系统进行了优化。结果表明,基于预测模型控制的直接转矩控制策略,与原有的基于最大转矩电流比的控制策略相比,更有利于降低电动车动力总成表面的振动响应。研究结果可为电动车动力传动系统的匹配、集成以及整体性能的提升提供参考。
电动车;动力总成;振动分析;最大转矩电流比控制;预测控制
电驱动动力总成作为纯电动车的重要部件,具有典型的机电一体化特点,其振动和噪声分析是目前研究的热点[1]。电动车动力总成的振动噪声问题具有无掩盖效应、机电耦合、磁固耦合等特点[2]。无类似内燃机的噪声掩盖将使得电机啸叫和齿轮啸叫噪声突出[3];机电耦合体现在电机转矩波动和机械传动系统的振动相互作用[4];磁固耦合体现在电机定转子间的径向和切向电磁力波对动力总成壳体振动和声辐射的影响[5]。这些新特性使电动车动力总成振动性能的研究有别于传统汽车,增大了振动控制的难度。
国内外学者对电动车动力总成振动的分析与优化主要集中在磁固耦合振动分析和机械结构的动力学修改方面,如MORI等[6-11],针对各类电动车用驱动电机进行了电磁力波获取、动力总成电磁振动分析及电机参数或者机械结构的动力学修改。但是,通过结构优化减小电磁振动可能增加电机的加工难度、提高制造成本、损失电机其它性能,倘若能通过改进驱动电机的控制策略,使其不仅能够减小电机输出的转矩脉动和各个方向电磁力谐波,同时能够减小动力总成的电磁振动,将更能体现电动车动力总成机电一体化的特点,降低工程实施的难度及成本,同时提高系统的控制性能。
然而,目前对于电动汽车驱动用电机控制策略的研究,主要关注与动力输出相关的性能,如提高动态响应速度和电机运行效率[12]、减小电机转矩脉动[13]、改善控制系统开关频率问题[14]以及不同控制策略输出性能的比较[15]等。进行电机控制策略对电动车动力总成振动性能影响的研究较少,更鲜见通过改进或者合理选择驱动电机控制策略,对动力总成进行振动控制的资料。
本文以典型集中驱动式电动车的动力总成为研究对象,进行考虑电机控制策略影响的建模、仿真、试验及策略改进,阐明了通过优选电机控制策略进行动力总成振动控制的有效性。
1 机-电-磁-控一体化建模
1.1 最大转矩电流比控制电机建模
所研究永磁同步电机采用SVPWM(空间矢量调制)方法,控制策略采用最大转矩电流比控制,搭建基于矢量控制的电机模型[4],如图1所示。
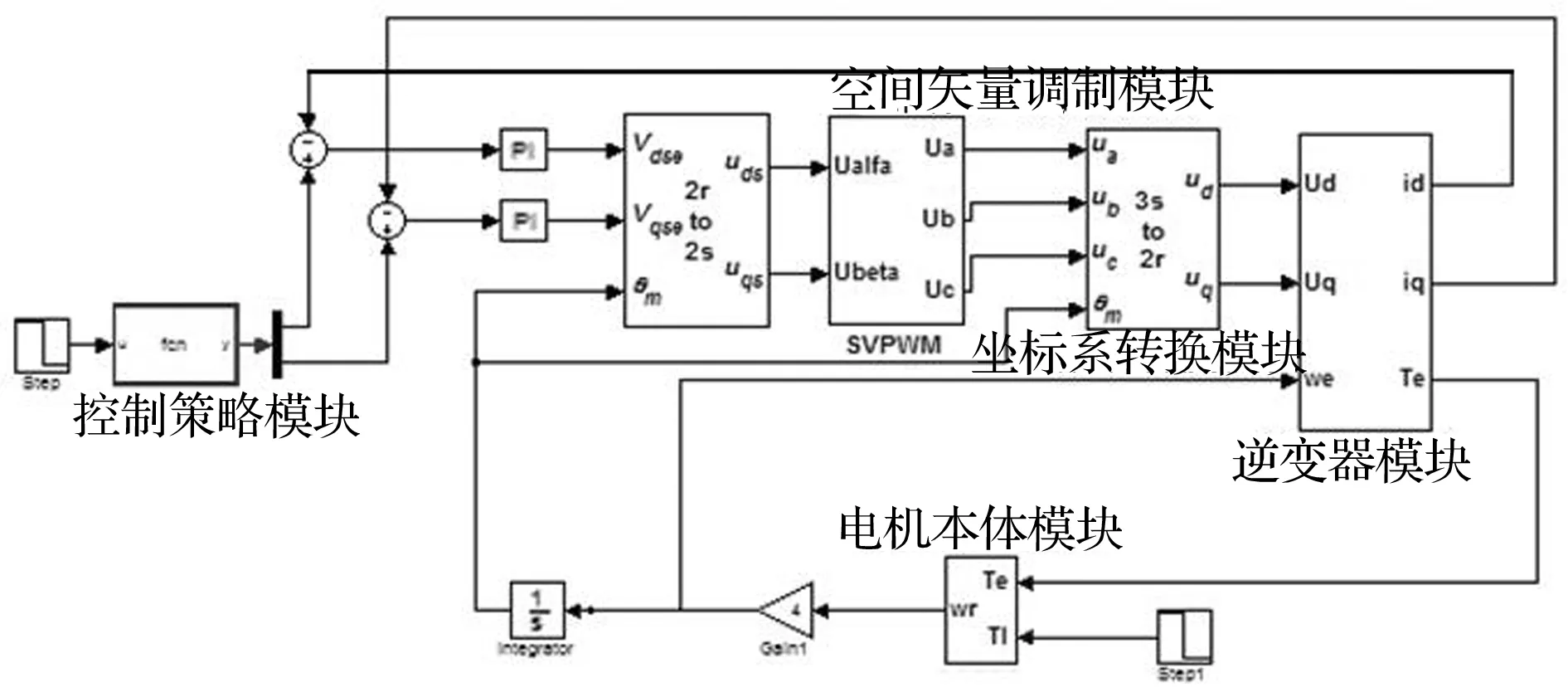
图1 永磁同步电机矢量控制模型Fig.1 Permanent magnet synchronous motor vector control model
采用最大转矩电流比控制时,转矩和定子电流之间满足如下的关系式:
Te=1.5np(ψfiq+(Ld-Lq)idiq)
(1)
(2)
模型中控制策略模块通过线性插值求解的方法得到的对应转矩指令下的参考电流。参考电流与实际电流的差值经PI调节后得到相应的参考电压,d、q轴的参考电压根据传感器采集的转子位置角,通过Park反变换得到定子两相静止坐标系下的参考电压供空间矢量调制使用,经空间矢量调制得到逆变器开关脉冲信号。开关脉冲信号送入逆变器输出接近于正弦波的电压驱动电机转动。
1.2 定转子电磁有限元建模
电机电磁力仿真的常用软件有Ansoft、JMAG等,考虑到后续电磁力与控制策略联合仿真的方便性,选择接口通用性相对较强的JMAG软件进行电机本体的电磁力仿真(使用Ansoft进行电磁力与控制策略的联合仿真,需要借助中间软件Simplorer的基础上用三种软件实现,计算量大,修改不便)。所搭建永磁同步电机的有限元仿真模型如图2示。
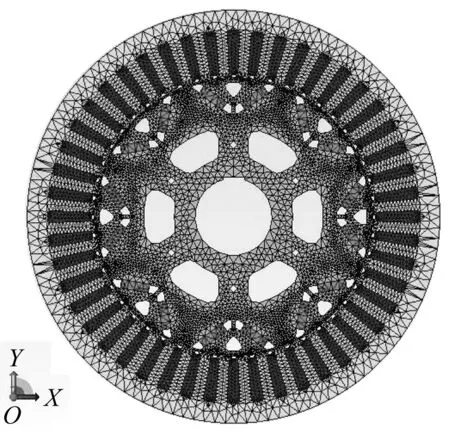
图2 电机电磁仿真模型Fig.2 Electromagnetic analysis model of motor
1.3 动力总成机械系统建模
电动车动力总成结构可参见文献[5],这里的改进之处是在文献[5]的基础上,进一步考虑了悬置支架、流体以及内部支撑对动力总成模态的影响。① 将三个悬置主动端(靠近动力总成的一端)考虑为柔性支架,对其进行模态分析,发现其主要振动模态频率在2 000 Hz~6 000 Hz之间,这将与动力总成壳体1 850 Hz~5 000 Hz之间的模态产生相互作用,故悬置支架必须体现在建模中,其模态试验结果也证明了考虑悬置支架的必要性[16];② 总成内部的流体主要有电机的冷却液以及减速器内部的润滑油。考虑这两类流体对结构特性的影响,将得到更加贴近试验结果的模态仿真结果。建模时假设冷却液充满整个壳体内水套,润滑油的储量设定为液面超过减速器二级传动副小齿轮最低点20 mm。冷却液和润滑油的模型建立,采用三维四面体网格,其精度能够满足工程要求[17];③ 总成内部支撑包括齿轮系统传动轴以及其端部支撑轴承,内部支撑将改变动力总成的约束情况,是建模中不可忽视的因素[3]。传动轴用Beam梁单元进行模拟,轴承用一簇Reb2单元模拟,用于连接传动轴端部和轴承座内孔表面单元。最终建立综合考虑总成结构及必要影响因素的有限元模型如图3所示。
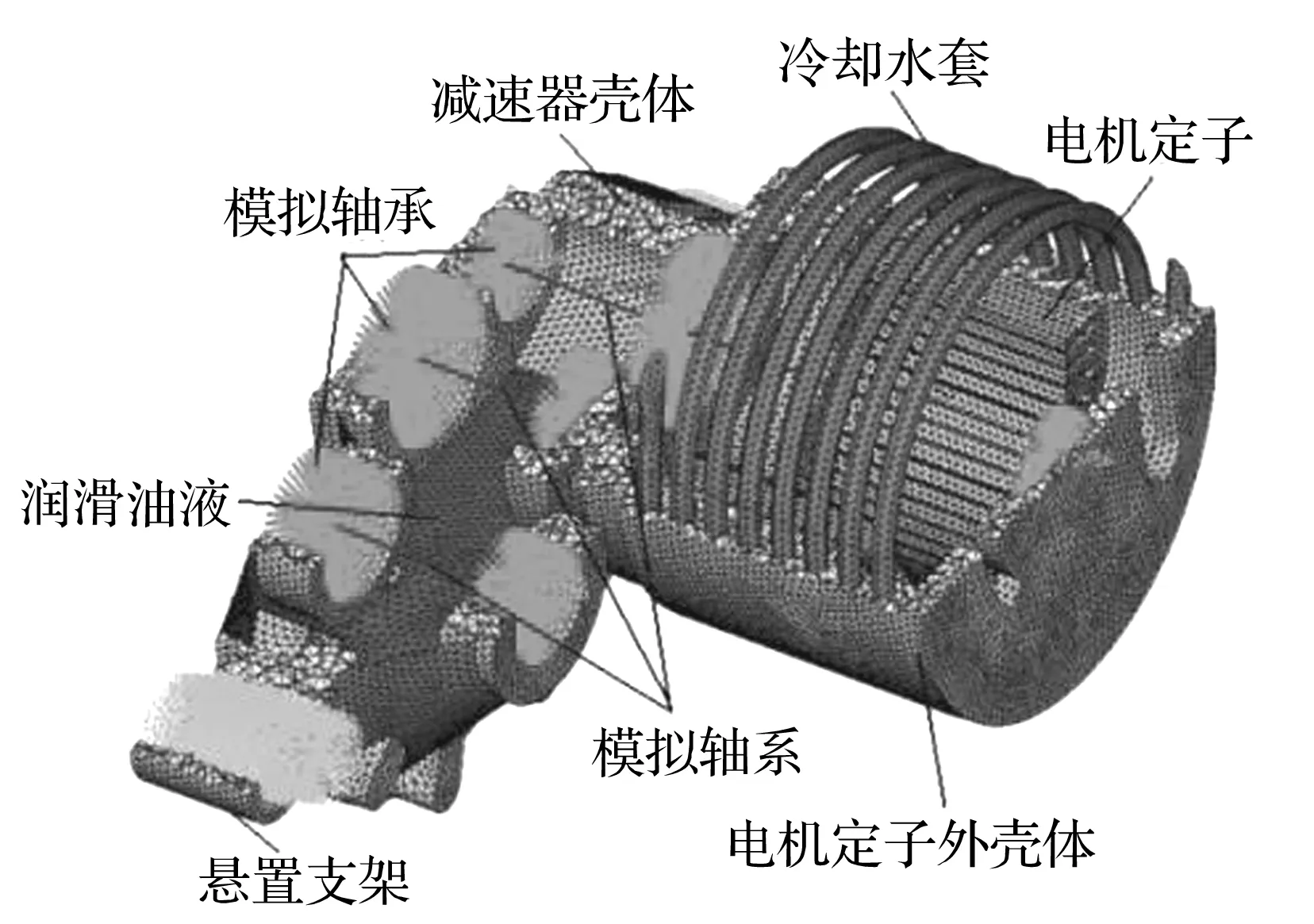
图3 动力总成有限元模型Fig.3 Finite element model of powertrain
为保证后续仿真、预测及优化的效果,对动力总成各个部件(电机定转子、减/差速器壳体、齿轮传动系统)及其组件模型的准确性进行了系统研究,通过对比部件/组件有限元模型的模态仿真结果和锤击试验结果,验证了建模方法的可行性。具体的模型搭建、仿真分析及试验对比,详见文献[18]。
2 多物理场仿真
2.1 电机电流
进行电机与控制策略的联合仿真,首先将JMAG电机模型生成对应的MATLAB可识别的S-Function模块,然后在MATLAB/SIMULINK中进行联合仿真,在此过程中需要添加接口,接口模块有三个输入,分别代表三相电源。设置完成后,将S-Function模块添加进控制策略,运行进行联合仿真。以某工况为例,仿真得到的电流输出结果如图4所示。
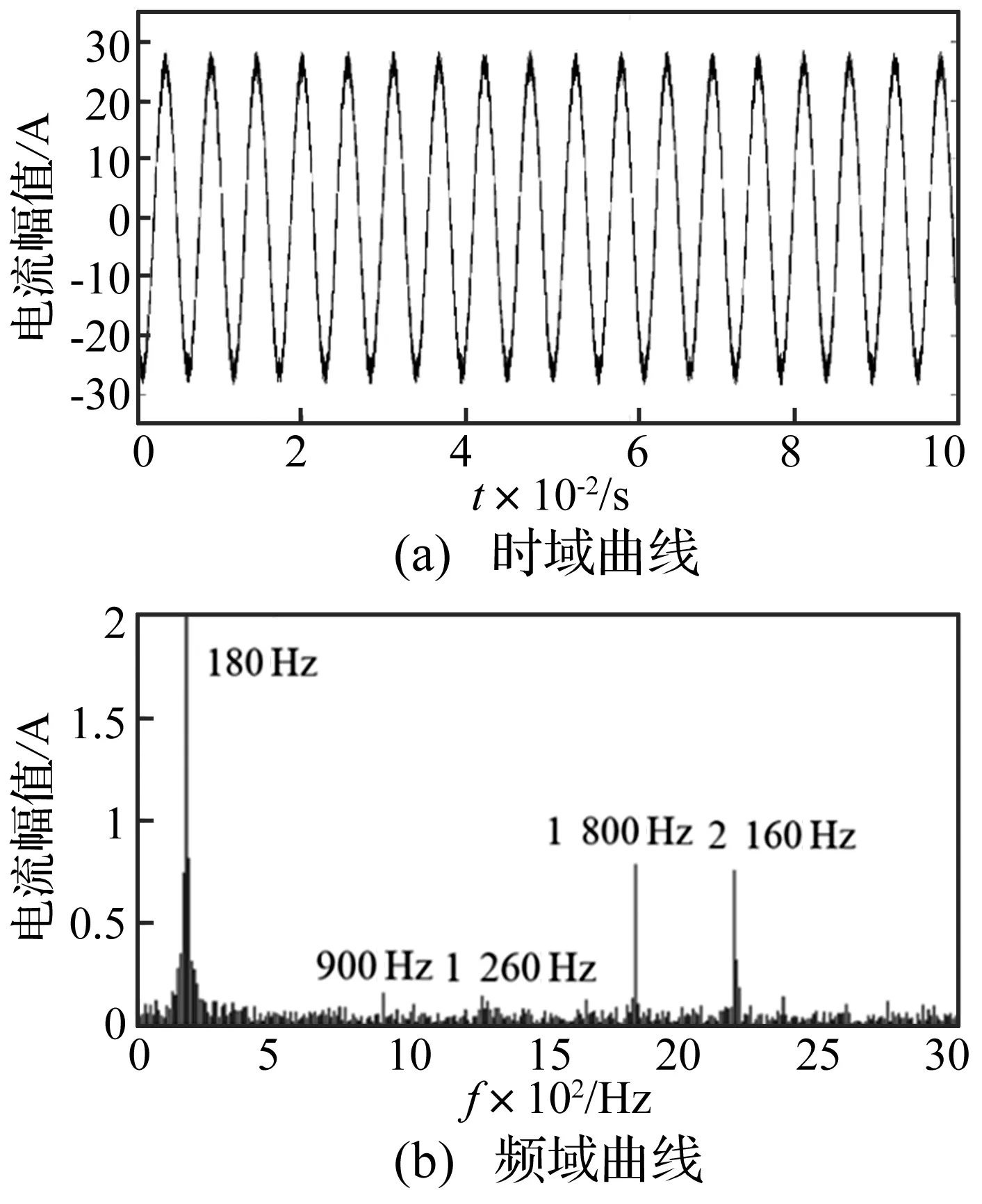
图4 稳态工况下某向电流Fig.4 Motor current under state condition
从图4(a)可以看出,考虑控制策略后,某相电流是与曲线不再是理想的正弦波,而是出现了一定的“毛刺”现象,进一步进行频域分析可知,主要的电流频率集中在180 Hz、900 Hz、1 260 Hz、1 800 Hz以及2 160 Hz。因为仿真工况为N=2 700 r/min=45 r/s,此时转子基频f0=45 Hz,电流基频f=pf0=180 Hz。所以这些主要频率点分别是电流频率的1倍频、5倍频、7倍频、10倍频以及12倍频,也就是转子基频的4倍频、20倍频、28倍频、40倍频以及48倍频。结合文献[4]对于激励特性的总结可以得出,引起这些倍频的原因分别是电流基波、电流谐波、偶数次谐波以及逆变器开关频率等; 20倍频和28倍频的波动将与齿轮系统的机械频率(10倍频和29倍频及其整数倍频率)耦合,产生较大的振动峰值,这是齿轮啸叫产生的主要原因。而4倍频和48倍频及其整数倍频率也将在该工况下引发较大的振动,进而产生电动车特有的电机啸叫噪声。结合文献[16]的模态分析结果可以预测出壳体系统将可能在2 000 Hz和其倍数频率4 000 Hz处产生共振,辐射较大噪声;结合文献[4]的传动系统仿真结果,还可以预测,电机的转矩波动将引发传动系统2 000 Hz的固有频率共振。
2.2 定子内表面电磁力
电磁力波是激发动力总成壳体振动噪声的主要激励源之一,首先使用JMAG软件提取联合仿真条件下作用在电机定子内部点的磁密,然后根据式(3)、(4)对磁密进行转换,得到定转子在输出力矩过程中对定子内部点的电磁力。
(3)
(4)
式中:磁导率常数μ0=4π×10-7,fr为径向电磁力密度,ft为切向电磁力密度,Br为径向磁密,Bt为切向磁密。在Matlab中计算得到感兴趣测点的径、切向电磁力随时间的变化关系图,然后进行傅里叶变换,得到电机壳体内部测点处径向、切向电磁力频谱图,如图5所示。
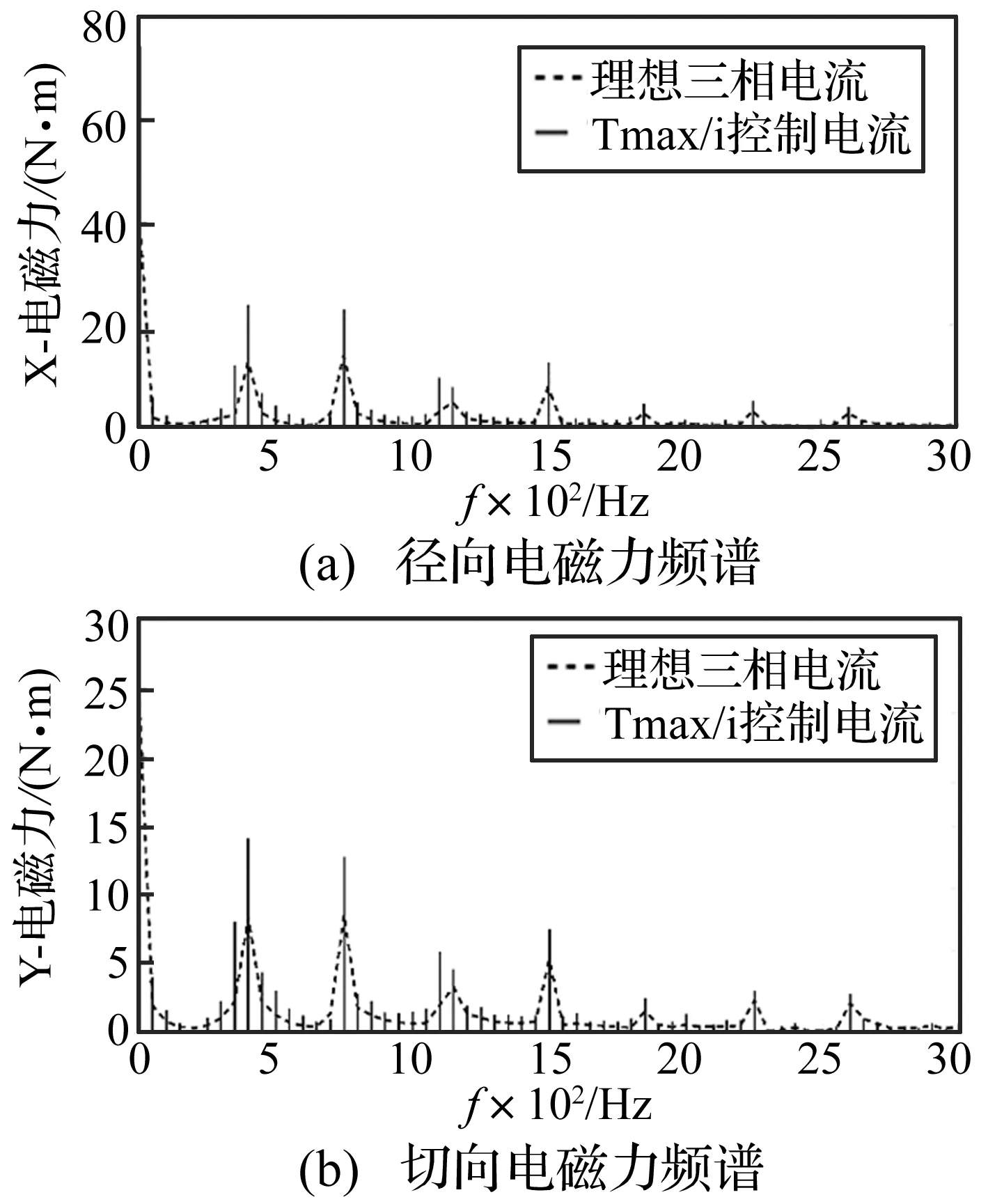
图5 电磁力频谱图Fig.5 Frequency domainof electromagnetic force
从图5(a)可以看出,考虑控制策略后,在控制电流的作用下,电机的径向电磁力波与理想电流供电条件下的径向电磁力波相比,几个主要频率点的峰值均有所升高,体现了考虑电机控制、引入电流谐波影响的必要性。如果使用理想的交流电进行仿真,将只能反映电机本体的电磁特性,不能反映电流对电磁力的影响,不利于进一步的有针对性的控制策略优化改进。切向电磁力的时频图也有类似的结论。径向、切向电磁力波在仿真工况下的振动峰值分别为400 Hz、750 Hz、1 100 Hz、1 500 Hz以及1 850 Hz,是后续优化的目标频率点。这些频率点峰值及其附近频率点振幅的降低程度将作为后续检验改进控制算法有效性的标准。
2.3 动力总成外表面振动响应
对动力总成模型进行动响应仿真及频谱分析,得到动力总成壳体各处的振动响应结果,可提取各感兴趣点的振动响应结果,以电机圆柱体中心某测点为例,仿真结果如图6所示。图中不仅给出了机械-电磁激励下的动态响应结果,还给出了机械激励和电磁激励共同作用下的结果,便于更加全面把握动力总成的振动特性,同时便于与试验结果进行对比。原因是,试验中很难直接测取电磁激励单独作用下的动态响应,往往获得的是机械-电磁激励综合作用下的振动响应。
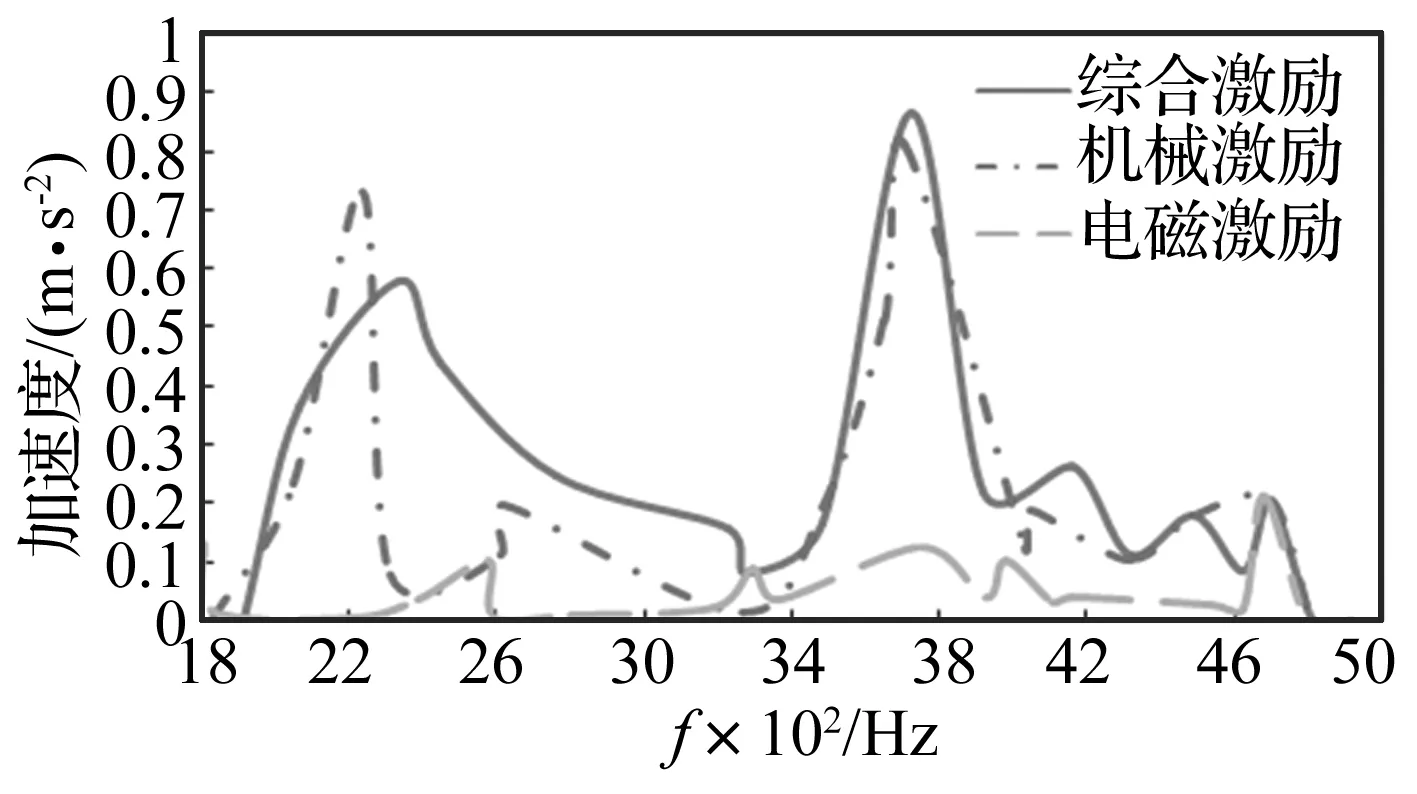
图6 电机仿真点X向加速度响应Fig.6 Acceleration of motor simulation point(X)
分析图6中各曲线可知:
(1) 动力总成壳体表面上的电机仿真点的振动响应,受到机械激励和电磁激励的综合影响。电机定子虽然不与减速器直接相连,但仍受到明显的机械系统振动激励的影响,表明动力总成一体化建模及仿真方法的优越性,若将电机和减/差速器分开建模则无法得到文中类似的结果。类似的,减/差速器虽然不直接受到定转子间电磁力的作用,但是其振动响应结果中也存在明显的电磁激励振动的成分。
(2) 机械激励单独作用下的动力总成振动响应和综合激励共同作用下的总成振动响应较为吻合,说明在0~5 000 Hz的频段内,机械激励占据主导因素,而电磁激励为次要因素。
(3) 机械激励作用下和综合激励作用下的特征频率主要分布在2 500 Hz、3 800 Hz以及4 500 Hz附近,对应文献[2]中的动力总成模态信息可知,主要引发了动力总成第5、6、10、14、15阶次的共振;引发这些共振的原因是转子-齿轮系统啮合频率的基频f的倍频,这些频率有z1倍(1 354 Hz)、2z1倍(2 708 Hz)、3z1倍(4 062 Hz)、z1 z3 / z2倍(490 Hz)、2z1z3/z2倍(980 Hz),z1、z2、z3分别为电机转子输出轴齿轮齿数、中间轴输入端齿轮齿数和输出端齿轮齿数。
(4) 电磁激励作用下的特征频率主要分布在2 000 Hz、2 400 Hz、4 800 Hz附近。结合图5和模态分析结果可知[2],2 000 Hz以下的径向、切向电磁激励幅值虽然较大,但是动力总成在该频段内的频率分布较稀疏,未能引发较大的壳体共振。2 000 Hz、2 400 Hz处的电磁激励虽然较小,但由于共振也出现了较明显的响应峰值,主要引发了总成第2、4阶次的共振。
综上所述,使用电磁仿真软件与电机控制策略相结合的仿真方法获取电磁激励,并将电磁力加载到动力总成的多物理场仿真方法,与以往研究相比能体现更丰富的动力学现象,便于分析电磁激励在振动响应中的贡献,为后续优化奠定基础。图8结果与文献[5]中的对应测点的仿真结果相比,峰值频率点更多,与理论分析结果更加吻合,体现了改进的仿真方法的优势。
3 动态响应试验
3.1 电流试验结果
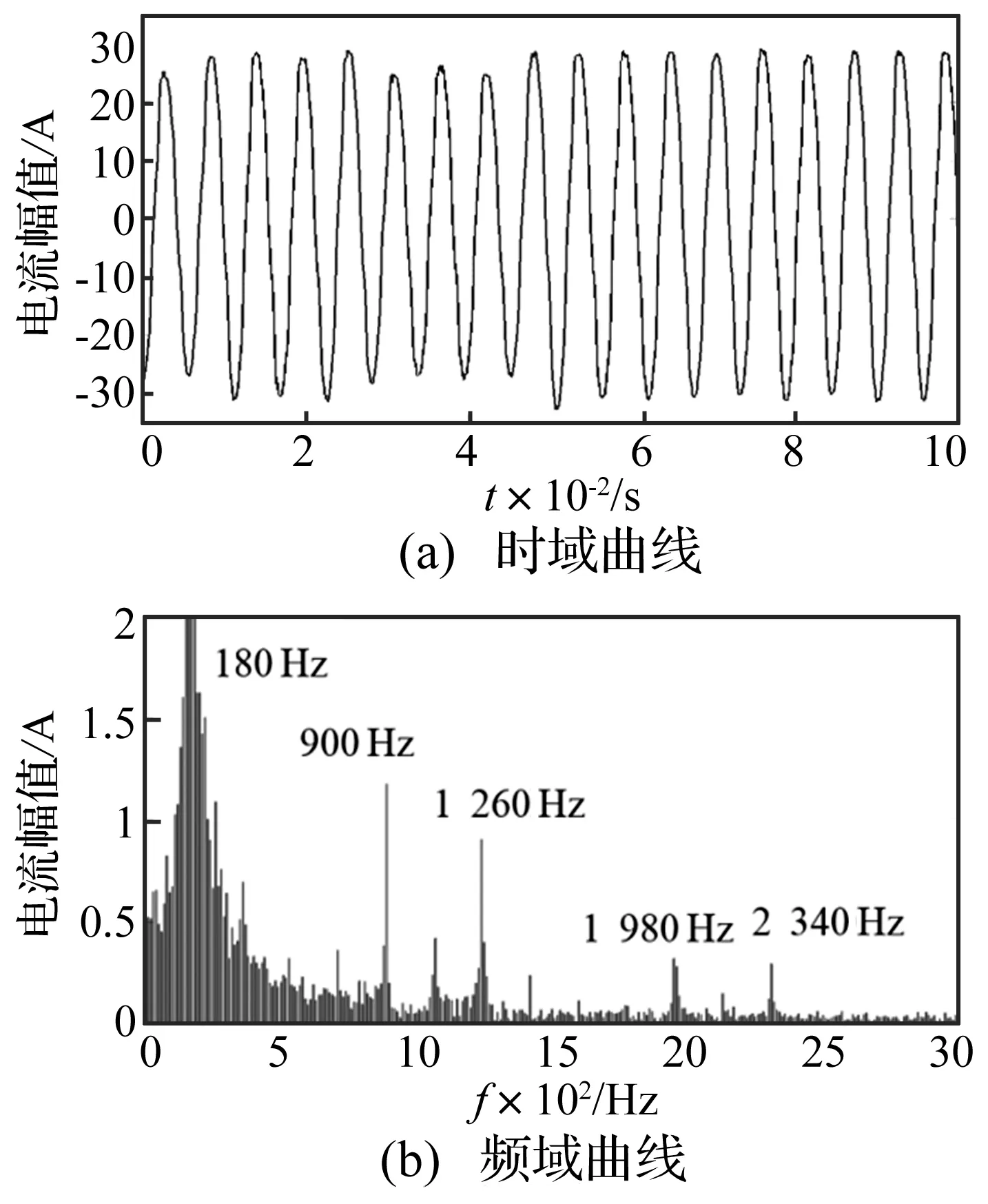
图7 稳态工况下某向电流Fig.7 Motor current under state condition
使用LeCroy HDO4034 高分辨率示波器记录某稳态工况下的电机输出电流,以仿真对应工况的电流为例,其时频分析结果如图7所示。从时域曲线看,与仿真工况相比,实测工况下的电流产生了更大的畸变,频域曲线也展示了更为丰富的频率峰值点。除了仿真中涉及的180 Hz、900 Hz、1 260 Hz外,还在720 Hz、1 080 Hz、1 440 Hz、1 980 Hz以及2 340 Hz处产生了较大的电流峰值,相关解释如下:
(1) 与仿真相同的180 Hz、900 Hz、1 260 Hz峰值点产生的原因是实际电流存在较大的谐波,这三个频率点的峰值高于仿真结果,是由于仿真时虽然由于考虑控制策略,一定程度上引入了电流谐波,但是对于控制因素之外的如电流检测误差并未认为设定,在实际系统中,由于直流偏移误差、相位误差以及增益误差的存在,会产生较高幅值的电流谐波,造成较大的转矩波动和电磁振动,这与文献[4]对于激励特性分析的结论一致。
(2) 与仿真相比有所偏移的1 980 Hz和2 340 Hz处的峰值代替了仿真中的1 800 Hz和2 160 Hz,也就是电流11倍频和13倍频代替了电流10倍频和12倍频(转子基频的44倍频和52倍频代替了40和48倍频)这些是由电机转子的静偏心引起,这些电流谐波偏移同样将引发壳体表面振动阶次的偏移。谐波次数偏移也使能量有所分散,主要峰值较仿真值有所减小。
(3) 比仿真多出的720 Hz、1 080 Hz以及1 440 Hz处的峰值,分别对应电流基频的4倍、6倍、8倍,也就是转子基频的16倍、24倍以及32倍频,也是因为实际中的定转子之间的静态和动态偏心引起。
另外,试验数据还展现了其它丰富的频率点,这些均是由于实际工作条件下存在的各类结构因素和控制因素所导致,本文只关注电机控制策略对动力总成振动响应的影响。
3.2 壳体振动响应
为了验证前述仿真结果的正确性,进行电动车整车转鼓试验。相关设备包括:纯电动车样车、三向加速度传感器以及记录、分析、处理振动信号设备:LMS Testlab、CANCASE/CANnape、LeCroy HDO4034 等。试验过程参照国家标准GB/T14365-93《机动车辆噪声测量方法》布置振动加速度传感器,主要测试工况为:在10 km/h~80 km/h稳速巡航条件下,每间隔10 km/h进行测量。以40 km/h的驱动工况处理结果为例进行分析,其加速度测点见图8。驱动试验工况对应机械-电磁综合激励下振动仿真工况。通过对比试验和仿真结果,可以在模态试验验证[16]的基础上,进一步验证模型的正确性。获取测点的振动加速度时域结果,并进行快速傅里叶变换(FFT),得到频域处理结果如图9所示。

图8 三向加速度传感器布置Fig.8 Position arrangement of acceleration sensor
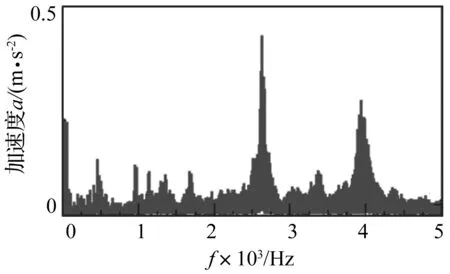
图9 电机试验点X向加速度响应Fig.9 Acceleration of motor test point (X)
将图9试验结果对比图7中的仿真结果可知,电机测点2 500 Hz和3 800 Hz处的由机械激励引发的峰值以及500 Hz、1 000 Hz、1 500 Hz附近的由电磁激励引发的峰值都在试验中被反映了出来;但在试验中第一峰值不是体现在3 800 Hz左右,而是出现在2 500 Hz左右,这是因为在实车动力总成系统中,由于装配误差和磨损等因素,造成转子轴相比仿真时较大的静、动偏心,从而引发的驱动小齿轮齿数的2倍频(2z1)的较大振动。减/差速器等其它测点的仿真和试验结果吻合的也较好,限于篇幅,未给出相关曲线。总体来看,试验结果和仿真结果中各个测点加速度的主要峰值点和峰值频率的趋势,具有较强的一致性,说明所提供的综合激励添加以及建模、仿真方法,可以较好的预测动力总成的振动特性,为进一步的从主动控制角度优化电机控制策略提供有效仿真平台。
4 控制策略优化
4.1 基于预测模型的直接转矩控制
模型预测控制(MPC)的实现方法是,在t采样时刻依据预测模型和假设的控制输入序列,预测未来一段时域内的状态,再在给定时域内在线求解一个优化问题来获得控制输入序列,但只将得到的控制序列的第一项应用到控制系统中,在t+1采样时刻,重复相同的过程,向前滚动优化。由于MPC 算法采用的是不断在线滚动优化,且在优化过程中不断通过实测系统输出与预测模型输出的误差来进行反馈校正,所以能在一定程度上克服由于预测模型误差和某些不确定性干扰等的影响,提高系统的鲁棒性。鉴于此,速度控制器采用MPC 控制代替经典的PID 控制算法。MPC 的预测模型分参数模型与非参数模型,选取离散状态空间模型作为速度控制器的预测模型。
永磁同步电机的机械运动方程为:
(5)
式中:Te、TL、J、Bv、ωr分别代表电机驱动转矩、传动系统负载转矩、电机转子惯量、黏滞阻尼系数以及转子输出角速度。取状态变量x=ωr,系统输入U=[Te,TL]T,系统输出y=ωr,则上式得状态空间表达式为:
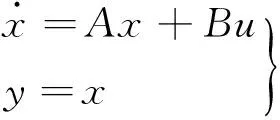
(6)
式中:A=Bv/J,B=[1/J,-1/J]。
通过上述公式前向差分将状态方程离散化,当两相邻离散点之间的时间间隔较小时,用一阶差商代替一阶导数:
(7)
令h=t(k+1)-t(k),即h为采样步长。将式(7)代入式(6)得到离散化状态空间表达式:
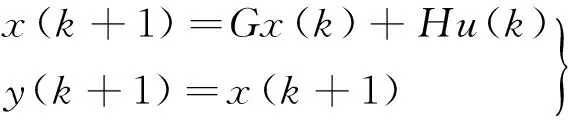
(8)
式中:G=1+hBv/J,H=h[1/J,-1/J],式(8)即为速度控制器的预测模型。其中控制输入中的第二项负载转矩TL作为可测的干扰,由于MPC对预测模型的精度要求不高,TL可根据式(5)直接计算得到。系统的期望输出是从现实实际出发且向设定值光滑过渡的一条参考轨迹规定的,通常取一阶指数变化的形式,即
(9)
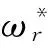
(10)
式中:Q为误差权系数矩阵,R为控制量权系数矩阵。由∂J(K)/∂Δu(k)=0可求得控制增量序列最优值,如式(11)。k时刻实际的控制量输入为u(k)=u(k-1)+Δu(k)。下一采样时刻,又重新计算,实现“滚动优化”。
Δu(k)=[G-1QG+R]-1×
GTQ[yr(k+1)-y(k+1)]
(11)
图10为基于预测控制的直接转矩控制仿真框图,椭圆中所示部分代表优化后的DTC控制策略将原先的PI控制器用一个MPC Computer替代,将当前转速测量值与期望值的偏差,经过MPC算法,得到后续的转矩参考值。MPC算法不仅能利用当前转速和期待转速的偏差值,而且可利用预测模型来预测两者未来的偏差值,以滚动优化确定当前的最优控制策略,使未来一段时间内当前转速与期望转速偏差最小。
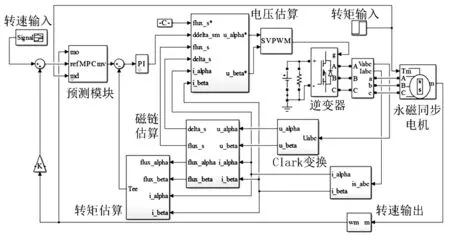
图10 优化DTC控制策略图Fig.10 Control strategy of optimized DTC
4.2 控制策略的振动抑制效果
使用前述多物理场仿真平台,仿真验证所提供的优化直接转矩控制对与振动的作用效果。图11、图12、图13分别为优化直接转矩控制条件下的电机输出转矩、电磁力输出以及总成壳体的振动响应。
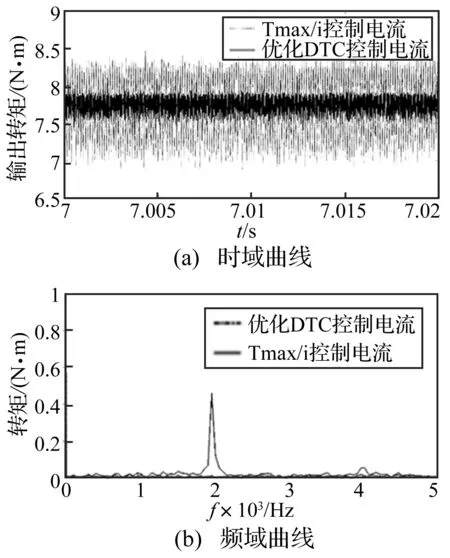
图11 转矩时频(稳态)Fig.11 Time domain of torque under state condition
图11为电机稳定后的电磁转矩图,与原有直接转矩控制条件下的转矩输出相比,单边振幅由原来的0.75 Nm减小到0.2 Nm,转矩波动的峰值频率点1 980 Hz及其倍频3 960 Hz处的波动幅值得到了明显的抑制,体现了优化直接转矩控制在抑制转矩波动方面的优势,这将进一步减小电机输出与传动系统的共振峰值(文献[4]结论:传动系统存在600 Hz、2 000 Hz左右的高频模态),降低传动系统的高频扭转振动,进而避免由于机电耦合振动造成的电机电流输出畸变和电磁力波谐波增多,有利于动力总成振动性能的提高。
从图12(a)可以看出,考虑优化的直接转矩控制控制策略后,电机的径向电磁力波时域图与最大转矩电流比电流供电条件下的径向电磁力波相比,波动幅值减小。从其频谱图也可看出,几个主要频率点的峰值均有所降低,尤其是高频谐波电流引发的高频电磁力大大减小,接近理想正弦波供电条件下的电磁力。体现了优化的直接转矩控制在调谐电磁力方面的优越性。切向电磁力的时频图也有类似的结论。径向、切向电磁力波在目标峰值频率点400 Hz、750 Hz、1 100 Hz、1 500 Hz以及1 850 Hz处的电磁力峰值的有效减小,有利于动力总成壳体表面由于电磁-结构因素引发的振动幅值降低。
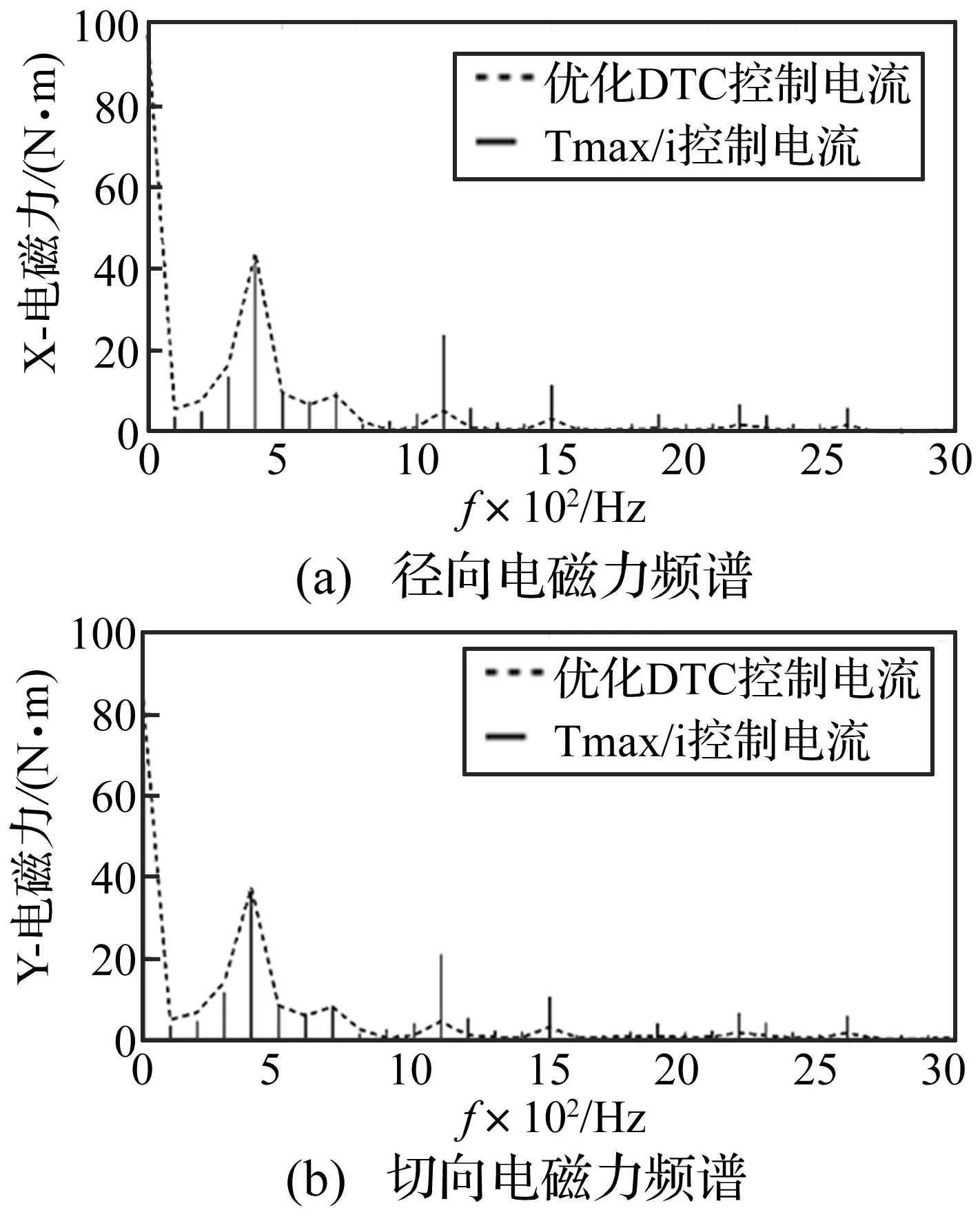
图12 电磁力频谱图Fig.12 Frequency domain of electromagnetic force
在电磁激励单独作用下,进行动力总成的多物理场仿真,查看控制策略优化前后,各个感兴趣测点的振动加速度响应。电机圆柱体中部某测点的各向加速度响应如图13所示。
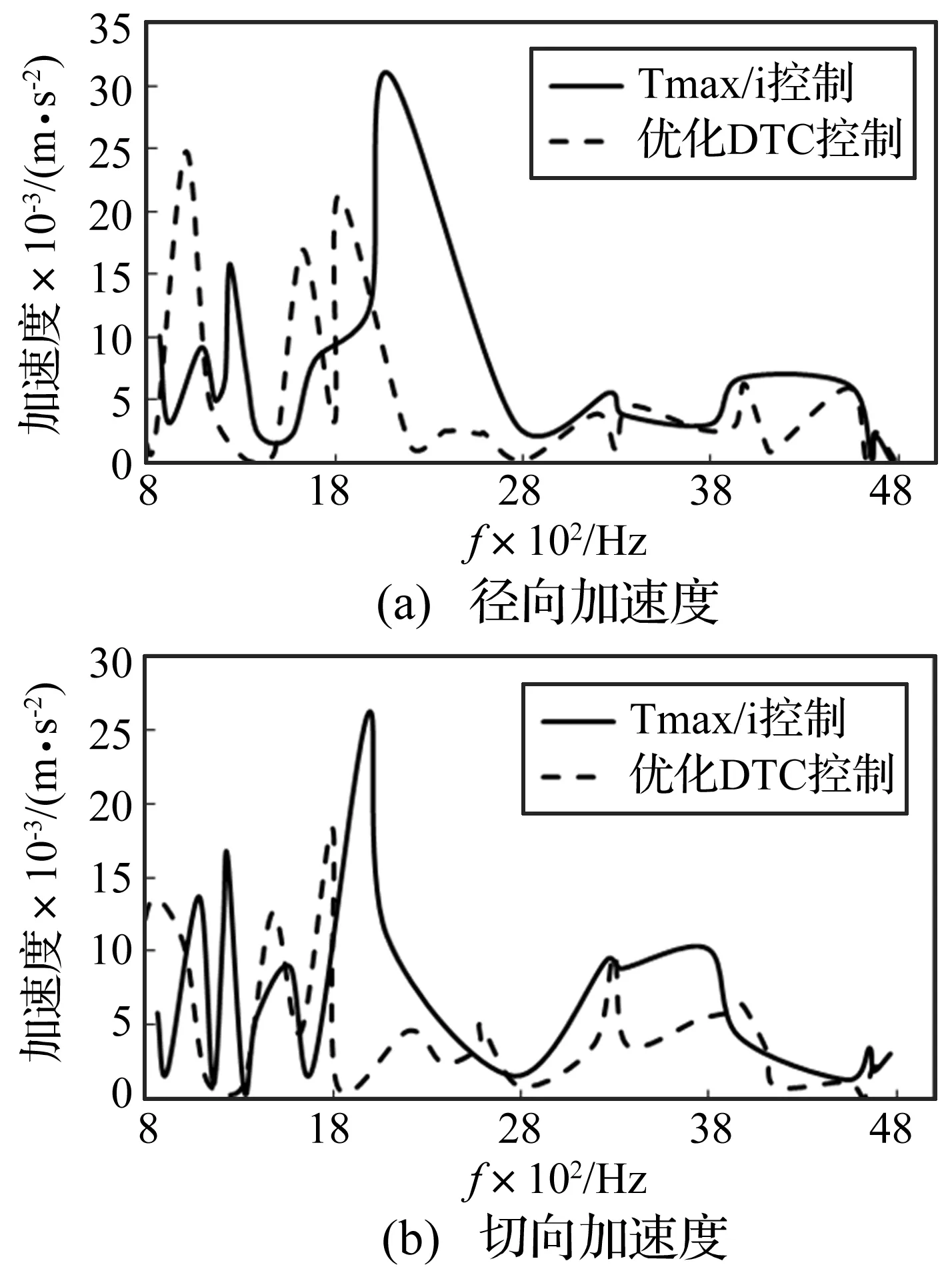
图13 电机测点振动加速度Fig.13 Time domain oftorqueunder state condition
从图13可以看出:
(1) 电机圆柱体径向(法向)加速度和切向加速度在关键频率点2 000 Hz和4 000 Hz处的振动峰值得到有效的抑制,其中2 000 Hz频率点处的振动峰值减小达0.01 m/s2。说明优化的电机控制策略在该工况下能够有效的抑制这两个频率点的电流、电磁力输出的波动,从源的角度减小电机输出引发动力总成在固有频率点共振的可能。这与前述电机转矩波动输出在这两个频率点的减小是吻合的,两者共同说明,优化的DTC控制方法能够在降低电机输出转矩波动的同时,抑制总成壳体的结构振动。
(2) 1 000 Hz和2 000 Hz左右的频率点处,振动峰值由于径向和切向电磁力的大幅减小(图12),得到了有效抑制。800 Hz~2 000 Hz频段的振动能量得以分散,结合动力总成模态分析结果可知[16],动力总成壳体的第1阶和第2阶固有频率分别为1 852 Hz、2 056 Hz,振动能量分布在1 800 Hz及以下,能够有效避免电磁激励引发的壳体高频共振,进而减小结构辐射噪声。
(3) 2 800 Hz~4 800 Hz高频段,振动幅值也有一定程度的减小,这与优化DTC控制方法的目标是减小电流谐波尤其是高频谐波,进而减小电磁力在高频段的阶次响应是一致的。
5 结 论
(1) 提出考虑电机控制策略影响的电动车动力总成机-电-磁-控多源振动仿真方法,阐明电机控制策略对电机电流、转矩、电磁力波以及壳体振动响应的影响,提出从改善电机控制策略的角度,降低电动车动力总成的振动响应的措施。
(2) 研究了原有控制策略对电动车动力总成振动的影响,探讨了基于预测模型控制的直接转矩控制方法在改善电动车动力总成振动性能方面的优势。其工程意义在于,可以考虑从电机驱动策略优化的角度有效降低转矩波动和动力总成壳体振动,从而避免对机械结构进行修改,缩短电动车传动系统开发的周期。
[1] 于蓬,贺立钊, 章桐,等. 集中电机驱动车辆动力传动系统 NVH性能研究现状与展望[J]. 机械设计,2014,31(3): 1-5.
YU Peng, HE Lizhao, ZHANG Tong, et al. NVH performance study of centralized motor driven vehicle power train[J]. Journal of Machine Design, 2014,31(3):1-5.
[2] 于蓬,王晓华,章桐,等. 集中式驱动纯电动车振动特性试验研究[J]. 振动与冲击, 2015, 34(14): 38-44.
YU Peng, WANG Xiaohua, ZHANG Tong, et al. Experimental study on vibration characteristics of central driven pure electric vehicle[J]. Journal of Vibration and Shock, 2015, 34(14): 38-44.
[3] 于蓬,章桐,冷毅,等. 电动车减/差速器振动特性分析及改进[J]. 振动与冲击, 2015, 34(7): 85-92.
YU Peng, ZHANG Tong, LENG Yi,et al. Vibration characteristics analysis and improvement of differential/reducer of electric vehicle[J]. Journal of Vibration and Shock,2015, 34(7): 85-92.
[4] 于蓬,章桐,孙玲,等. 集中驱动式纯电动车动力传动系统扭转振动研究[J]. 振动与冲击, 2015, 34(10):121-127.
YU Peng,ZHANG Tong,SUN Ling,et al. Powertrain torsional vibration study of central-driven pure EV[J]. Journal of Vibration and Shock,2015, 34(10): 121-127.
[5] 于蓬,陈霏霏,章桐,等. 集中驱动式电动车动力总成系统振动特性分析[J]. 振动与冲击,2015, 34(1): 44-48.
YU Peng,CHEN Feifei,ZHANG Tong,et al. Vibration characteristics analysis of a central-driven electric vehicle powertrain[J]. Journal of Vibration and Shock,2015,34(1): 44-48.
[6] MORI D, ISHIKAWA T. Force and vibration analysis of induction motors[J]. IEEE Transactions on Magnetics,2005,41(5): 1948-1951.
[7] PELLEREY P, LANFRANCHI V, FRIEDRICH G. Coupled numerical simulation between electromagnetic and structural models[J]. IEEE Transactions on Magnetics, 2012,48(2):983-986.
[8] KIM D, NAM J, JANG G. Reduction of magnetically induced vibration of a spoke-type IPM motor using magnet mechanical coupled analysis and optimization[J]. IEEE Transactions on Magnetics,2013, 49(9): 5097-5105.
[9] DUPONT J, AYDOUN R, BOUVET P. Simulation of the noise radiated by an automotive electric motor: influence of the motor defects[J]. SAE Int. J. Alt. Power,2014, 3(2):310-320.
[10] 何吕昌. 电动汽车用永磁直流无刷驱动电机电磁噪声研究[D].上海:同济大学,2012.
[11] 张增杰. 小功率永磁同步电动机振动噪声的计算与分析[D].沈阳:沈阳工业大学,2013.
[12] 尚重阳,邓利红,周建华,等.一种永磁同步电动机的最大转矩电流比控制方法[J]. 自动化技术与应用,2008,27(7): 90-92.
SHANG Chongyang, DENG Lihong, ZHOU Jianhua, et al. Maximum torque per ampere control for permanent magnet synchronous motor[J]. Automation Technology and Application, 2008, 27(7): 90-92.
[13] 王斌,王跃,郭伟,等. 基于定子磁链降阶状态观测的永磁同步电机无差拍直接转矩控制系统[J]. 电工技术学报, 2014, 29(3): 160-171.
WANG Bin, WANG Yue, GUO Wei, et al. Deadbeat direct torque control of permanent magnet synchronous motor based on reduced order stator flux observer[J]. Transactions of China Electro technical Sosiety, 2014, 29(3): 160-171.
[14] CASADEI D, SERRA G, TANI A. Implementation of a direct control algorithm for induction motors based on discrete space vector modulation[J].IEEE Transactions on Power Electronic, 2000, 15(4): 769-777.
[15] CASADEI D, PROFUMO F, SERRA G. FOC and DTC two viable schemes for induction motors torque control[J]. IEEE Transactions on PE, 2002,17(5): 779-787.
[16] 陈诗阳, 于蓬, 章桐, 等. 电动车动力总成模态及振动响应仿真研究[J]. 机电一体化, 2015(4): 32-38.
CHEN Shiyang, YU Peng,ZHANG Tong,et al. Simulation study on modal and vibration response of an EV powertrain[J]. Mechatronics,2015(4): 32-38.
[17] 项昌乐,焦开河,王文平,等. 箱体结构动强度的流固耦合有限元分析[J]. 兵工学报, 2007, 28(7): 769-773.
XIANG Changle, JIAO Kaihe, WANG Wenping,et al. Fluid-structure interaction finite element analysis of dynamic structural strength on gearbox’s housing[J]. Acta Armamentarii, 2007, 28(7): 769-773.
[18] 方源,章桐,于蓬,等. 电动车动力总成有限元建模方法的研究[J]. 机械传动,2015(9):20-25.
FANG Yuan,ZHANG Tong,YU Peng,et al. research of the mothed of finite element modeling of an electric automotive powertrain[J]. Journal of Mechanical Transmission,2015(9):20-25.
Vibration analysis of electric vehicle powertrains considering motor control strategy
YU Peng1,2, ZHANG Tong1,2,3, YU Yao1,2, GUO Rong1,2
(1. New Clean Energy Automotive Engineering Center, Tongji University, Shanghai 201804, China;2. School of Automotive Studies, Tongji University, Shanghai 201804, China;3. Sino-German College of Applied Sciences, Tongji University, Shanghai 201804, China)
Aiming at structural vibration problems of EV powertrains, a simulation method with mechanical-electrical-magnetic-control integration was proposed, and the optimization of control strategy was conducted. Firstly, a powertrain model considering motor control strategy, motor electromagnetic action and detailed mechanical structure was established reflecting the characteristics of electromechanical integration. Then simulations and tests for motor current,electromagnetic forces and vibration response of a powertrain were conducted the correctness of the multi-physical field simulation method was verified. Lastly, the system was optimized through control strategy improvement instead of mechanical structure modification. Results showed that compared with the maximum torque per ampere control strategy, the direct torgue control strategy based on predictive model control is more suitable to reduce the surface vibration responses of EV powertrain. The study results provided a reference for the integration of EV powrtrain system and the improvement of its overall performance.
electric vehicle; powertrain; vibration analysis; maximum torque per ampere control; predictive control
国家863计划项目(2011AA11A265);国家自然科学基金(51205290);中央高校基本科研业务费专项资金项目(1700219118)
2015-07-02 修改稿收到日期:2015-10-16
于蓬 男,博士,1986年生
章桐 男,博士,教授,博士生导师,1960年生
E-mail:tzhang@fcv-sh.com
U469.72
A
10.13465/j.cnki.jvs.2016.19.009
