淹没磨料射流涡旋特性大涡模拟及研究

张欣玮， 卢义玉， 周 哲， 汤积仁

(1.重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400030；2.重庆大学 复杂煤气层瓦斯抽采国家地方联合工程实验室，重庆 400030)



淹没磨料射流涡旋特性大涡模拟及研究

张欣玮1,2， 卢义玉1,2， 周 哲1,2， 汤积仁1,2

(1.重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400030；2.重庆大学 复杂煤气层瓦斯抽采国家地方联合工程实验室，重庆 400030)

基于涡运动理论，采用固-液两相大涡模拟方法模拟了淹没磨料射流的涡量场，分析了涡旋扩散机理与卷吸特性以及磨料随涡运动在射流中的混合分布规律。流场剪切层中涡旋呈对称分布，沿轴线方向涡量呈指数衰减，衰减到最小值两侧涡旋混合成紊流混合区，而等速核内涡量几乎为零。相比于纯水射流，磨料的存在使得射流涡运动减弱，涡旋扩散角减小约50%，等速核增长约30%，减少了能量耗散。磨料在射流束内部时，受涡旋影响，趋向分布于高应变率、低涡量区，在涡旋下游侧磨料浓度最高。同时模拟研究了磨料参数对涡量场的影响规律，结果表明：磨料参数基本不影响扩散角(14.1°～15.1°)、等速核长度，卷吸能力随磨料浓度、粒径、密度的升高均呈现小幅度地降低，磨料密度对其影响程度最大，磨料粒径的影响最不明显。

淹没射流；磨料；涡旋；大涡模拟

磨料射流在石油、采矿等领域得到了广泛地应用与推广[1-3]。在淹没条件下，由于射流本身与周围水介质间的黏滞作用，产生大量涡旋，由此而产生能量交换与动量耗散[4-5]。涡旋的产生使得射流对磨料产生卷吸混合等作用，决定了磨料在流场中的分布，研究涡旋产生的机理与磨料混合的过程对充分利用磨料射流的能量具有重要意义。

国内外学者关于水射流的涡旋特性进行了一系列的研究。STOIC等[6-7]认为水射流与周围介质的混合会使混合层表面形成大涡，同时从周围环境中卷入介质，而周围介质从水射流中吸取能量，后由于涡量扩散，涡旋长大至一定程度后自行融汇于湍流中；NOVARA等[8]认为在湍流混合层的运动学特性中，二维涡旋结构起着主要作用。LI等[9-10]进行了相关的研究，认为涡旋引起的卷吸作用对工程应用具有重大意义，但目前关于此方面的研究仅限于理论分析，并没有相应的实验或模拟来验证，有待进一步研究。XIAO等[11]采用气-液两相大涡模拟方法研究了低速射流遇气流的涡旋特性，周卫东等[12-13]采用固-液两相数值模拟方法模拟了磨料射流的流场，但是关于固-液两相的大涡模拟方法鲜见报道，并且采用该方法来研究磨料射流的涡旋特性具有一定前瞻性。

由于目前在研究磨料射流的流场分布方面没有合适的实验方法，本文通过流场涡理论分析，结合固-液两相大涡模拟来研究磨料射流在淹没条件下的涡旋产生与扩散机理，以及磨料在涡量场中的混合与分布规律，与纯水射流流场对比分析磨料的作用，并探究在不同磨料参数(粒径、密度、浓度)对涡量场的影响规律。

1 流场结构与磨料分布规律

根据淹没条件下水射流运动特性，喷嘴外流场可分为初始段和主体段，如图1所示。由涡运动的理论，可知射流一离开喷嘴就与周围介质发生剧烈的动量交换和紊动扩散，产生一系列涡旋，但仍有一部分处于中心线附近的射流介质保持喷嘴出口速度，这部分介质组成了等速核心[14]。在等速核心的内部不存在横向或纵向的速度梯度，因此该区域是处处无旋的。在初始段的边界与等速核心之间，则是由射流介质与周围介质互相掺混而形成的混合区，也称作剪切层，该区域内涡旋呈轴对称分布，并沿射流轴线方向逐渐扩散，射流与周围流体的动量交换就在该区内进行。

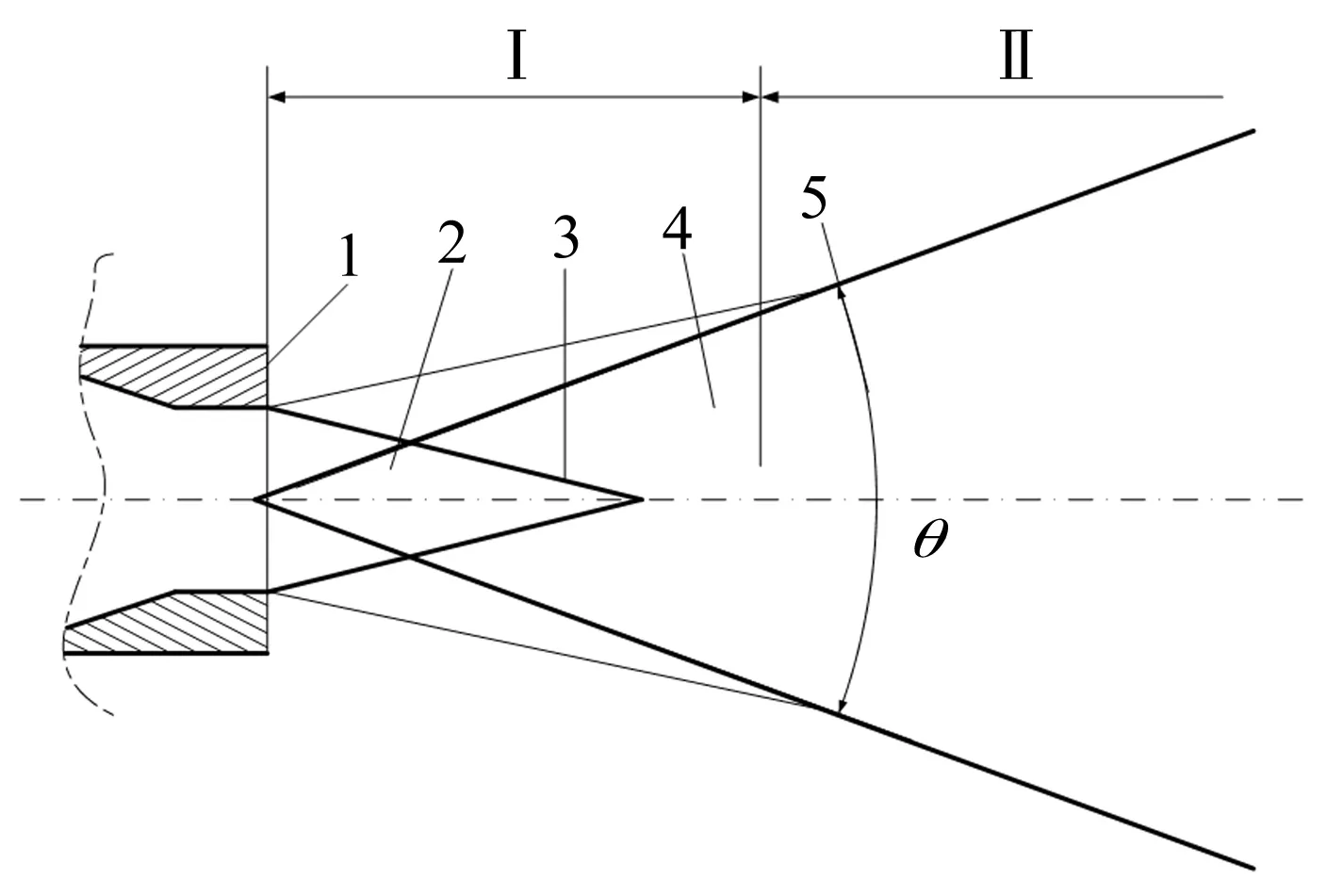
Ⅰ.初始段；Ⅱ.主体段；θ.扩散角1.喷嘴；2.等速核心；3.内边界；4.剪切层；5.紊流混合区图1 水射流流场结构图Fig.1 The structure of flow field of water jet

射流主体段内是一个紊流混合区，它与初始段混合区没有本质的区别，只是在该段内紊动强度增加，被卷吸的环境介质增多，混合区内的平均速度逐渐减小，该段内以螺旋涡为主。

在射流轴向方向上存在着许多涡旋，且存在着涡旋配对，涡旋的运动可以大大增加磨料的扩散。磨料在射流束内部时，其运动有一种集中分布于高应变率、低涡量区的趋势，磨料浓度分布如图2所示。在涡旋附近，应变率、涡量是不均匀的，在涡核区其涡量很大，在靠近涡核的下游，正是一个高应变率、低涡量区，磨料集结在这里。

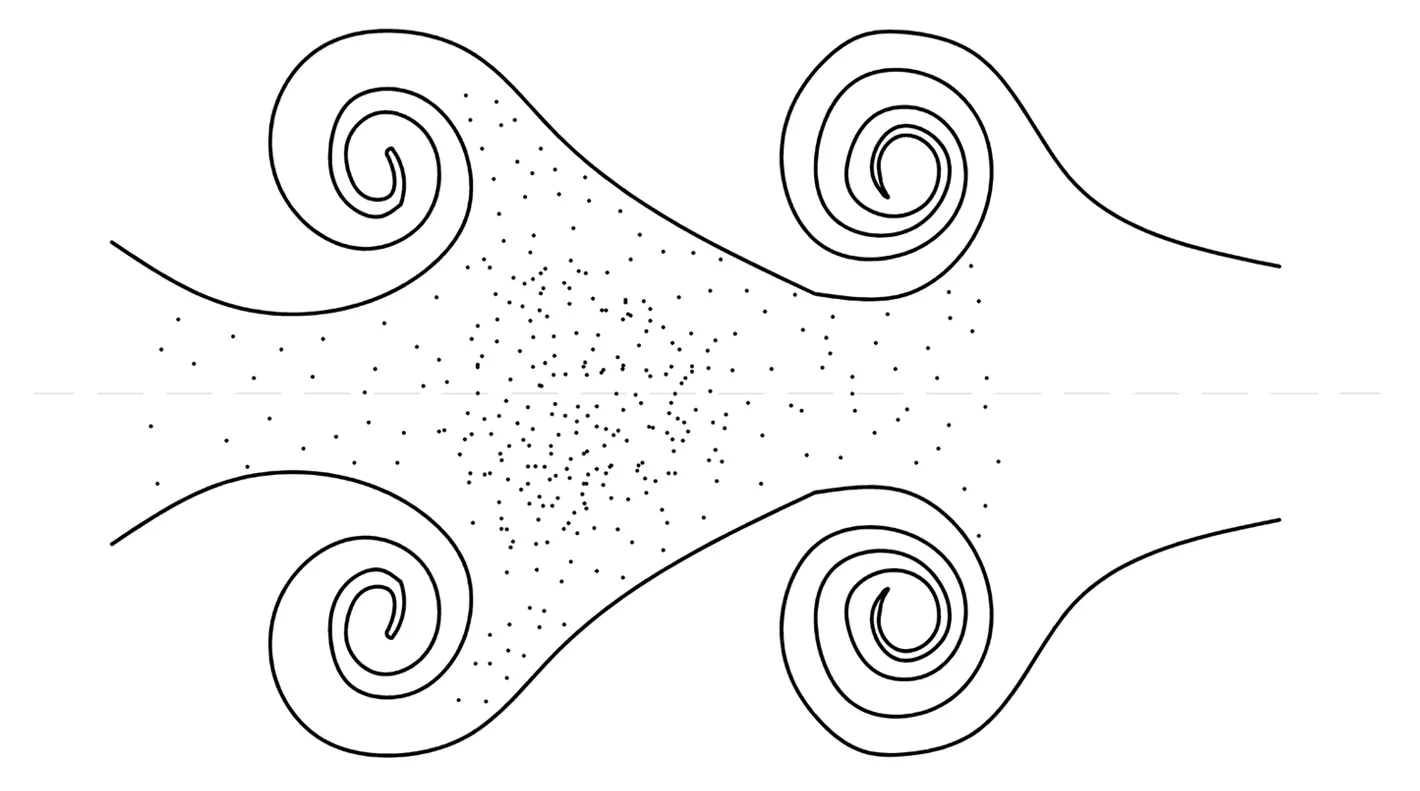
图2 磨料分布示意图Fig.2 The diagram of particle distribution

同时，涡旋具有强大的能力把射流束外的磨料卷入涡中随涡旋运动。根据流体力学的观点，在涡核截面上，其通道截面最小，因而这里速度最高、压力最小，磨料一旦在这一区域通过，受连续相速度的影响得到加速。但一旦经过这一区域，通道面积迅速加大，因而磨料连同流体速度又下降，上游速度大，下游速度小，磨料自然在下游集结，与原射流中的磨料混合在一起。这就是射流产生涡旋卷吸磨料，磨料得到加速混入主流一起运动的过程。

2 固-液两相大涡模拟

目前，射流流场数值模拟方法分为雷诺平均模拟(RANS)、直接数值模拟(DNS)和大涡模拟(LES)。RANS模型将所有流体涡设定为各向同性并统一作雷诺平均，无法得到流场细节，DNS则需要计算所有尺度的流体涡，对计算机的容量和运算速度要求高，目前仍难以模拟大雷诺数的复杂湍流流动，而大涡模拟方法将流体涡分为大、小两种尺度，仅对足以表征流场细节的大尺度涡进行直接数值模拟，因此既能得到射流涡旋结构，又具有实用性。

另外，多相流模拟方法包括VOF模型、混合模型(mixture模型)、欧拉模型和离散相模型等。其中离散相模型遵循Euler-Lagrange方法，而VOF模型、混合模型和欧拉模型遵循Euler-Euler方法。VOF模型主要用于计算气液两相流。由于磨料射流固相体积分数较高，所以也不选用离散相模型。混合模型和欧拉模型都适用于固相体积分数较大的情形，虽然混合模型不如欧拉模型精确，但在计算时所占的资源较少，计算时间也较快，在处理多相流时也能得到较满意的结果，并且当存在大范围的颗粒相分布或界面规律不清晰时，欧拉模型就不适合，同时考虑欧拉模型与LES 方法不能兼容的问题，因此，两相流模型选用混合模型进行求解。

2.1 固-液两相大涡模拟的数学模型

在实施大涡模拟方法时，必须把大涡流场和小涡流场分开，以便对大涡流场实施模拟计算，对小涡流场建立模型。大涡流场是对实际流场进行过滤从而将小于网格尺度的小涡过滤掉而得到的，这一过程是借助于滤波函数来进行。在大涡模拟方法中将瞬时流动变量分解成大尺度量和小尺度量，其大尺度量可以通过一个在物理区域上的加权积分来表示。

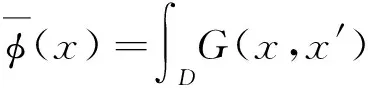
(1)

式中:G(x,x′)为空间滤波函数，D为流体计算控制域。过滤函数定义为：

(2)

式中:v为计算单元的体积。

对于等温液固两相流动中，瞬时的液相质量和动量守恒方程进行滤波，可得：

(3)

(4)

同样，利用滤波函数对固相质量和动量方程进行滤波处理，可以得到固相LES方程组：

(5)

(6)

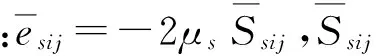
式(4)和式(6)中Mls为液体与颗粒之间的作用力，反映了液相与颗粒相之间的动量交换。考虑到粗糙网格中，颗粒相的微观尺度结构被过滤掉了，因此相间曳力表达式为：

(7)

式中:βe为颗粒-流体之间有效曳力系数，在本研究中，采用Ergun方程和Wen和Yu方程计算。

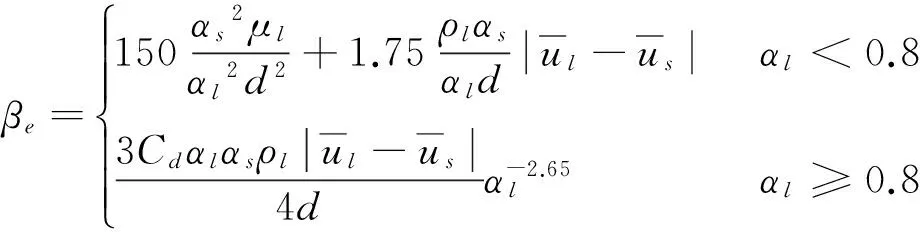
(9)

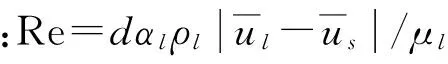
2.2 边界条件及网格划分

计算结构：出口直径3.2 mm，计算宽度为30 mm，长度为150 mm，如图3所示，边界条件包括压力入口、壁面和压力出口。设定出口压力为0，不同的入口压力5 MPa、10 MPa、15 MPa、20 MPa、25 MPa，磨料粒径分别取0(纯水无磨料)、0.01 mm、0.05 mm、0.1 mm，磨料密度分别取2.2 g/cm3、2.4 g/cm3、2.6 g/cm3、2.8 g/cm3、3.0 g/cm3，体积浓度分别取4%、6%、8%、10%、12%，进行大涡模拟，探究涡旋产生和扩散的机理与磨料的分布规律，对比分析磨料的作用，并得到磨料参数对磨料射流涡旋特性的影响规律。

图3 计算流域及边界属性Fig.3 Calculation geometry and border property

为保证大涡模拟的计算精度，网格划分全部使用结构网格，并在壁面及射流边界处加密，网格间距0.1 mm，划分网格数量约为55 243个。

2.3 计算方法和收敛判据

离散选用中心差分格式(Central Differencing Scheme)，并使用PRESTO格式修正压力梯度，流场计算使用SIMPLE算法。时间步长为射流通过网格时间的1/3，即1.0×10-6s，计算时间为射流流经整个计算区域所需时间的3倍，即0.005 s。在迭代过程中，对解的收敛性进行监视，并在系统达到指定精度后结束迭代计算，认为计算结果收敛。

2.4 模拟结果分析

在有旋流动流场的全部或局部区域中充满着绕自身轴线旋转的流体微团，形成了一个由涡量w表示的涡量场[15]，涡量的大小代表了流场中各点旋度的大小，涡量大说明流体微团的旋转角速度大，流场扰动剧烈，有利于强化流体传质[16]，对周围介质的卷吸能力较强。

二维流场涡量的表达式为：

(10)

式中:，ux为在质点横向(x)的速度；uy是质点竖向(y)的速度。

图4为大涡模拟得到的相同工况下纯水射流与磨料射流的涡量场。可知，两种射流的涡量场均与水射流流场结构图(图1)吻合良好，流场分为等速核、剪切层、紊流混合区三个区域。等速核心内涡量处处为零，不存在速度梯度，几乎不进行能量交换，是射流能量最集中的部分。剪切层中涡旋涡量均呈对称分布，喷嘴出口处产生涡旋，沿着射流方向涡旋直径渐渐扩大，而涡量值则不断衰减，表明射流发展过程中，涡旋与周围介质进行能量、物质交换，卷入周围介质后使得射流束直径增大，卷吸范围逐渐扩大，能量也逐渐耗散，卷吸能力逐渐减弱。

同时，两种射流的涡量场呈现出一定的差异。磨料射流表现出集束性收敛性，纯水射流则要发散的多，磨料射流能量集中于磨料，与周围介质间的黏滞作用减弱，能量交换减少，卷吸范围较小。纯水射流的涡旋呈现一个个独立的螺旋涡的形状，而磨料射流的涡旋是连续的。总的来说，纯水射流的卷吸能力更强些。

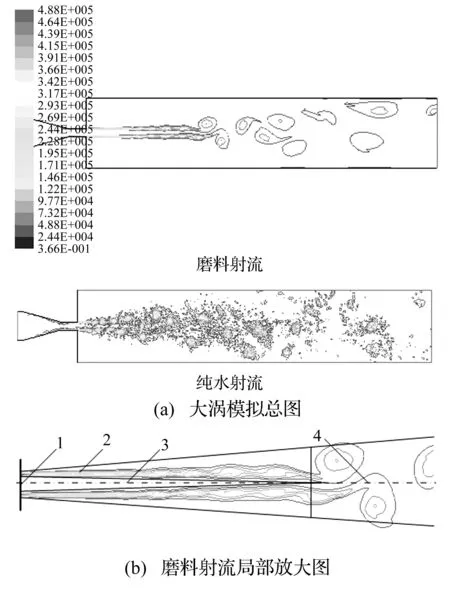
1.喷嘴；2.等速核心；3.剪切层；4.紊流混合区图4 大涡模拟涡量场图Fig.4 The vorticity field chart of large eddy simulation

图5 磨料浓度分布图Fig.5 The particle concentration distribution

结合图5与图4(a)的磨料射流，很好地验证了磨料的分布集中在低涡量区的观点，磨料随着涡旋的运动产生团聚现象。在剪切层内，涡旋分布密集且涡量较大，该区域磨料浓度很低，涡旋核心区域几乎为零；无旋的等速核心中磨料浓度较高，约为12%～13%(初始磨料浓度8%)，集结于涡旋下游侧，且与涡旋的形状基本吻合。紊流混合区中，磨料随涡旋成团分布，浓度分布比较混乱，团聚区磨料浓度最高，而螺旋涡分布区磨料浓度又几乎为零。

3 磨料对涡旋特性的影响规律

由于磨料与水介质存在不同的物理力学性质，在相同入口出口压力条件下，磨料射流与纯水射流的涡量场表现出一系列的差异。根据模拟结果，以喷距为横轴，涡旋中心点涡量为纵轴，连接同一压力的数据，结果如图6所示，该图中所选磨料射流参数：磨料浓度8%、密度2.6 g/cm3、粒径1 mm。

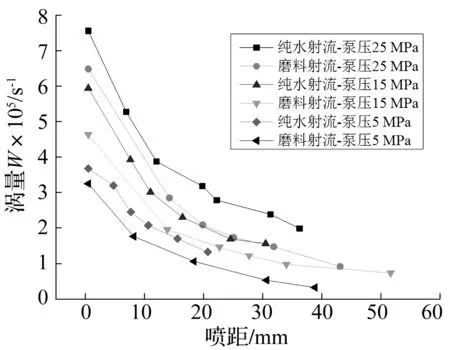
图6 涡量与喷距的关系Fig.6 The relationship between vorticity and spray distance

可知，在同一压力条件下，任一喷距磨料射流的涡量值均小于纯水射流，是由于磨料与周围水介质之间的黏滞作用远小于射流水与周围水之间的，因此相同工况下磨料射流与周围介质的黏滞作用相对较低，射流束剪切层内的水介质产生的速度梯度较小，涡量值也较小，对周围介质的卷吸能力较弱。

数据还反映了峰值涡量产生于喷嘴出口段，表征了涡旋产生时的能量大小，由此向外扩散产生卷吸，同一流场内，峰值涡量较大的，之后任一喷距涡量值均较大，因此，峰值涡量并非随机产生的，而是决定了整个流场中涡量值的大小，考察该值来反应流场情况是可靠的。之后随着射流喷射距离增加，涡量值呈指数衰减，涡旋沿着射流喷射方向逐渐扩散，卷吸周围介质，使其获得速度和能量，而射流束本身的能量则逐渐下降，因而射流的卷吸能力逐渐衰减。

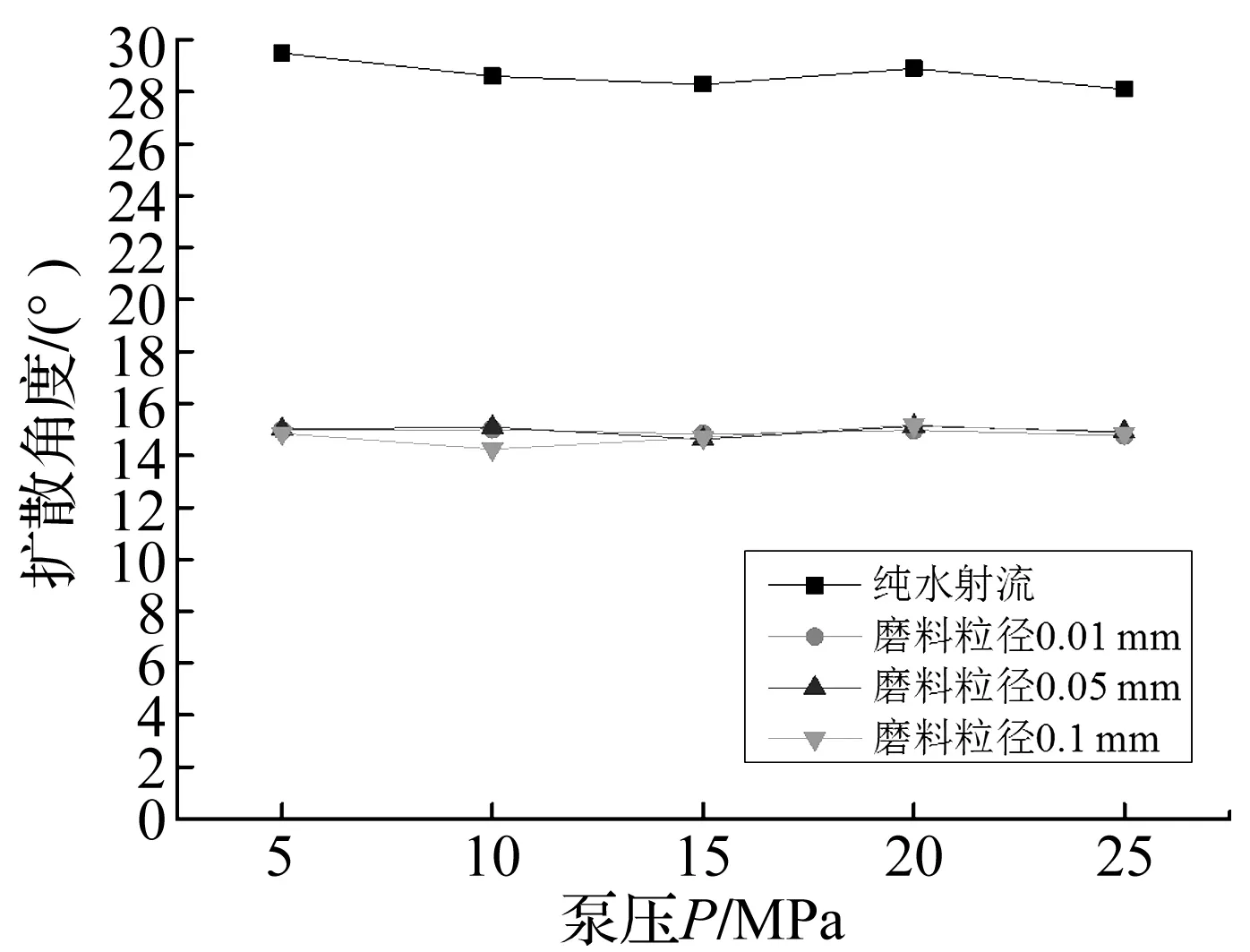
图7 扩散角度与泵压的关系Fig.7 The relationship between diffusion angle and pump pressure

磨料射流相对纯水射流呈现明显的集束性、收敛性。处理模拟数据，得到各个工况下涡旋扩散角度，来表征射流的发散/收敛程度。如图7所示，可认为涡旋扩散角度几乎不随泵压的变化而变化，纯水射流的涡旋扩散角约为28.1°～29.5°，而加入磨料后，扩散角显著降低，大约在14.1°～15.1°之间，降低了约50%，是由于磨料射流的能量主要集中在磨料上，射流与周围水介质间的黏滞作用减弱，涡旋扩散减弱，从而减少了射流束的紊动扩散与能量耗散，也因此磨料射流具备很强的冲击能力。同时，还呈现磨料粒径小范围地增大扩散角几乎不变化。

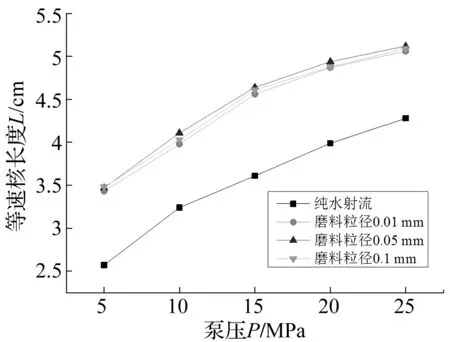
图8 等速核长度与泵压的关系Fig.8 The relationship between the length of patential core and pump pressure

磨料射流的收敛性同时使得等速核长度增长，如图8所示。随着泵压升高，射流束所获得的能量增加，等速核长度呈现线性增大，且随粒径增大几乎不变化。而磨料射流等速核长度普遍比纯水射流增加了30%左右，与扩散同理，是由于磨料的存在减少了射流束本身与周围介质的能量交换，射流束内部核心部分就不容易受到干扰而产生速度梯度，无旋部分增长，从而能量集中的等速核部分增长。

综上，磨料的存在使得射流与周围介质产生的涡旋强度降低，扩散范围减小，能量交换减少，因此磨料射流主流能量集中而具有很强的冲击能力。涡旋的存在还会不断地卷入从击打面折返回淹没水中的磨料，对其进行卷吸加速并混合，进行二次利用。

4 磨料参数对涡旋特性的影响规律

同时，通过该方法研究了磨料参数对涡量场的影响规律，包括磨料粒径、磨料浓度、磨料密度，结果如图9、10所示。

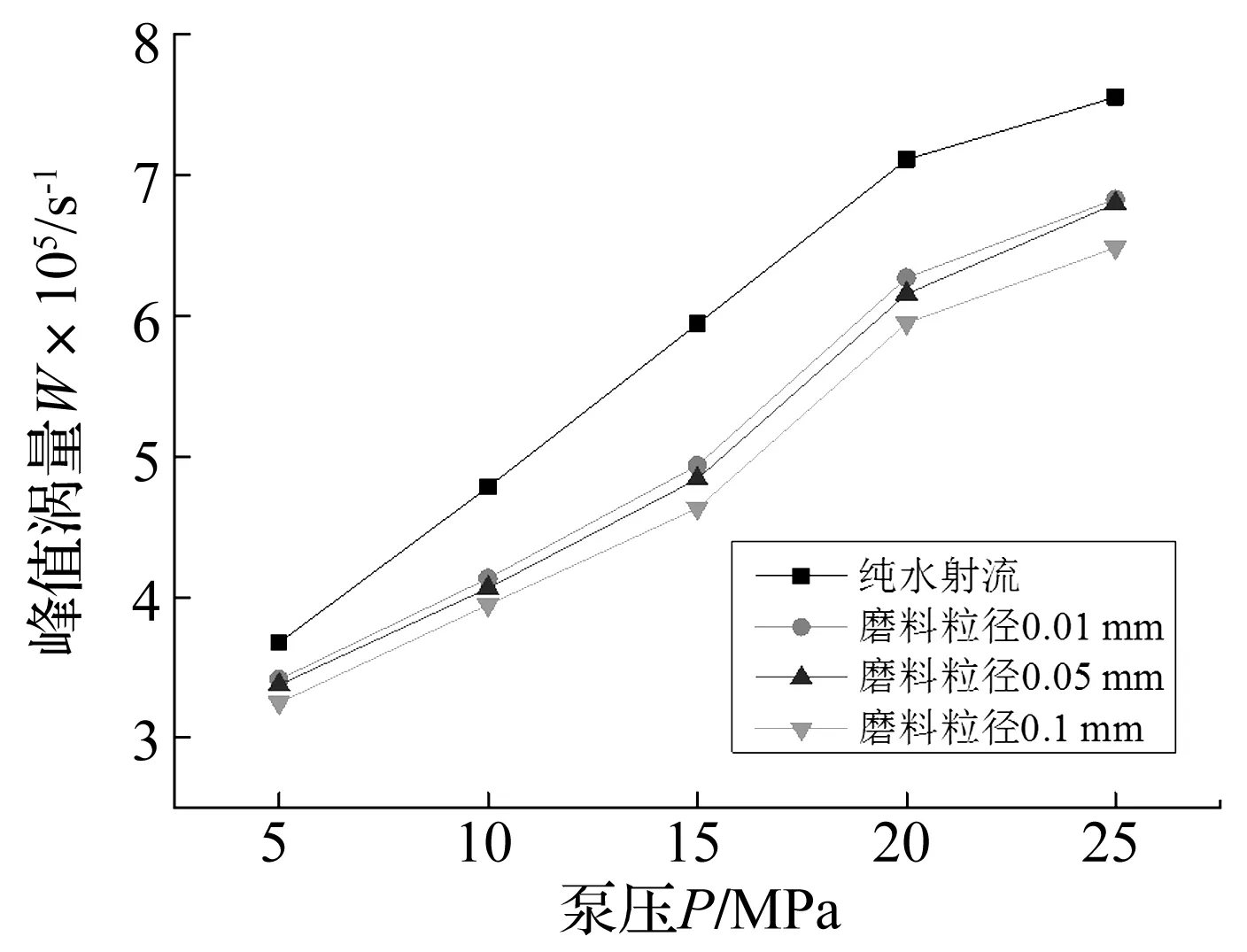
图9 峰值涡量与泵压的关系Fig.9 The relationship between peak vorticity and pump pressure

图10 峰值涡量与磨料浓度、密度的关系Fig.10 The relationship between peak vorticity and abrasive density and concentration

结果表明，卷吸能力随着磨料粒径、密度和浓度的升高均呈现不同程度的降低。这一点是不同于射流的破岩效率的，各磨料参数对破岩的影响均呈抛物线规律，存在一个最佳的磨料粒径、密度及浓度值，而对于涡旋特性并不存在。随着磨料浓度、粒径、密度的升高，水与周围介质的黏滞作用不断地小幅度地降低，总的来说影响程度：磨料密度>磨料浓度>磨料粒径。其中，磨料粒径的影响最小，因为当密度与浓度不变时，粒径增大意味着颗粒数的减少。由于模拟方法的限制，磨料的粒径最大只能做到1 mm，根据分析推测粒径更进一步增大，会引起涡量值先减小后增大，有待进行下一步改进模拟方法来研究。

5 结 论

(1) 采用固-液两相大涡模拟方法模拟了淹没条件下磨料射流的涡量场，结合射流流场涡运动理论证实该方法可行。

(2) 流场剪切层中涡旋呈对称分布，且沿轴线方向涡量呈指数衰减，衰减到最小值两侧涡旋混合于紊流混合区，等速核内处处无旋。磨料在射流束内部时，其运动有一种集中分布于高应变率、低涡量区的趋势。

(3) 相比于纯水射流，磨料的存在使得射流涡运动减弱，涡旋扩散角度减小约50%，等速核心增长约30%，减少了能量耗散。

(4)随着磨料浓度、粒径、密度的升高，水与周围介质的黏滞作用不断地小幅度地降低。

[1] 雷鹏,倪红坚,马琳,等. 自吸环空流体式自激振荡脉冲粒子射流调制机制分析[J]. 中国石油大学学报(自然科学版), 2014(3):80-86.

LEI Peng, NI Hongjian, MA Lin,et al. Mechanism analysis for self-oscillation pulse particle jet based on automatic fluid sucking from annulus[J]. Journal of China University of petroleum(Edition of Natural Sciences), 2014(3):80-86.

[2] 赵健,徐依吉,邢雪阳,等. 脆性岩石粒子冲击理论模型与实验[J]. 中国矿业大学学报, 2014(6): 1108-1112.

ZHAO Jian, XU Yiji, XING Xueyang, et al. A theoretical model and experiment of brittle rock impacted by particles[J]. Journal of China University of Mining & Technology, 2014(6): 1108-1112.

[3] 黄中伟,李根生,史怀忠,等. 围压下磨料射流喷射套管及灰岩实验研究[J]. 中国石油大学学报(自然科学版), 2014(6): 85-89.

HUANG Zhongwei, LI Gensheng, SHI Huaizhong, et al. Experimental study on abrasive water jet blasting casing and limestone under ambient pressures[J]. Journal of China University of petroleum(Edition of Natural Sciences), 2014(6): 85-89.

[4] MLYNARCZUK M, SKIBA M, SITEK L, et al. The research into the quality of rock surfaces obtained by abrasive water jet cutting[J]. Archives of Mining Science,2014,59(4):925-940.

[5] AYDIN G. Recycling of abrasives in abrasive water jet cuttingwith different types of granite[J]. Arabian Journal Geosciences, 2014, 7(10): 4425-4435.

[6] STOIC A, DUSPARA M, KOSEC B, et al. The influence of mixing water and abrasives on the quality of machined surface[J]. Metalurgija, 2014,53(2): 239-242.

[7] CHEIN R, CHUNG J N. Effects of vortex pairing on particledispersion in turbulent shear flows [J]．International Journal of Multiphase Flow,2007,13 (6)：785-802.

[8] LIEPMANN D. The role of streamwise vorticity in the near-field entrainment of round jets[J]. Journal of Fluid Mech, 2012, 245 :643-668.

[9] SCARANO N M. Performances of motion tracking enhanced Tomo-PIV on turbulent shear flows [J]. Experiments in Fluids, April,2012,52(4):1027-1041.

[10] 曲海,李根生,黄中伟,等. 水力喷射分段压裂密封机理[J]. 石油学报, 2011(3): 514-517.

QU Hai, LI Gensheng, HUANG Zhongwei, et al. Sealing mechanism of the hydrajet stepwise fracturing[J]. Acta Petrolei Sinica, 2011(3): 514-517.

[11] XIAO F, DIANAT M, MCGUIRK J J. LES of turbulent liquid jet primary breakup in turbulent coaxial air flow[J]. International Journal of Multiphase Flow, 2014, 60: 103-118.

[12] 周卫东,李罗鹏,孔垂显,等. 淹没条件下长圆喷嘴流场数值模拟[J]. 中国石油大学学报(自然科学版), 2013(1): 80-84.

ZHOU Weidong, LI Luopeng, KONG Chuixian, et al. Numerical simulation of flow field of nozzle with elliptical exit under submerged condition[J]. Journal of China University of petroleum(Edition of Natural Sciences), 2013(1):80-84.

[13] 姜玉颖,龚烈航,徐新林,等. 磨料水射流喷嘴内流场数值模拟[J]. 兵工学报,2014(4):461-467.

JIANG Yuying, GONG Liehang, XU Xinlin, et al. Numerical simulation of flow field in abrasive water jet nozzles[J]. Acta Armamentarii, 2014(4): 461-467.

[14] 李晓红, 卢义玉, 向文英. 水射流理论及在矿业工程中的应用[M]. 重庆: 重庆大学出版社, 2007.

[15] 白静,方红卫,何国建. 非淹没丁坝绕流的三维大涡模拟研究[J]. 力学学报,2013(2):151-157.

BAI Jing, FANG Hongwei, HE Guojian. Study of non-submerged groin turbulence flow in a shallow openchannel by les [J]．Chinese Journal of Theoretical and Applied Mechanics，2013(2):151-157.

[16] 王小兵,刘扬,崔海清,等. 垂直管中定常螺旋流涡量特性的PIV试验研究[J]. 流体机械,2012(2):5-9.

WANG Xiaobing, LIU Yang, CUI Haiqing, et al. Experimental study on the fluid flow characteristics in the hydrocyclone on the PIV[J]. Fluid Mechinery, 2012(2):5-9.

Vortex characteristics of submerged abrasive jet with large eddy simulation

ZHANG Xinwei1,2, LU Yiyu1,2, ZHOU Zhe1,2, TANG Jiren1,2

(1. State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400030, China;2. National & Local Joint Engineering Laboratory of Gas Drainage in Complex Coal Seam, Chongqing University, Chongqing 400030, China)

Based on the theory of vortex motion, the vorticity field of submerged abrasive jet were simulated using the two-phase large eddy simulation method. The mechanism of eddy diffusion and entrainment were analyzed, the abrasive distribution law with vortex movement in the jet was acquired. It was shown that the vortex distribution of the shear layer in the flow field is symmetrical; vorticity at both sides of the vortex mixing presents an exponential attenuation to the minimum value, the vortex mixing forms a turbulent mixing zone; the potential core is irrotational everywhere; compared with pure water jet, the existence of abrasive makes vortex motion abate, the eddy diffusion angle decreases by about 50% and potential core grows by about 30%; the abrasive affected by vortex tends to be distributed in the area of high strain rate and low vorticity; abrasive concentrates in the downstream side of vortex. The influence law of abrasive parameters on the vorticity field was also studied with simulation. The results showed that the diffusion angle(14.1°～15.1°) and the potential core length basically remain unchanged with variation of abrasive parameters; the entrainment ability decreases slightly with increase in abrasive concentration, particle size and density.

submerged water jet; abrasive jet; vortex; large eddy simulation

国家重点基础研究发展计划(2014CB239206)；国家自然科学基金青年基金项目(51404045)；长江学者和创新团队发展计划(IRT13043)

2015-09-17 修改稿收到日期：2015-10-15

张欣玮 女，博士生，1991年生

卢义玉 男，博士,教授，博士生导师，1972年生

TE319

A

10.13465/j.cnki.jvs.2016.19.001