引信圆柱螺旋压缩弹簧制造误差对抗力的影响
2018-08-27张义强王雨时
张义强,王雨时,闻 泉
(南京理工大学 机械工程学院, 南京 210094)
我国引信制造用弹簧钢丝符合GJB1497—1992《特殊用途碳素弹簧钢丝》规定。这是目前国内性能最好的一种弹簧钢丝,但价格也最昂贵。在相同直径下,其极限抗拉强度指标比其他任何弹簧钢丝都高,直径精度也比同直径的其他钢丝产品高。尤为独特的是,为了控制加工弹簧时几何尺寸和抗力的散布,该标准还规定同一盘钢丝直径尺寸之差:直径不大于1.0 mm时不得超过0.01 mm,直径大于1.0 mm时不得超过0.015 mm。因此在钢丝制造业中,亦称其为高级弹簧钢丝。各种引信弹簧都是比较重要的性能件,设计时要求比较多,如耐高冲击、小体积以及长期贮存各项指标稳定等。在弹簧结构参数中,对设计与工艺影响最大的就是钢丝截面形状和尺寸,特别是直径精度。文献[1]介绍钢质引信弹簧,表面镀锡后抗力约增加10%。文献[2]揭示了引信弹簧钢丝圆度对抗力的影响,但并未进一步揭示抗力与截面形状的关系。文献[3]分析了弹簧钢丝加工工艺对小型压缩弹簧性能的影响,但并未涉及弹簧几何制造误差对抗力的影响。本文将主要分析引信圆柱螺旋弹簧几何制造误差对抗力产生的影响,但并不包括节距误差时的影响,这部分内容另文讨论。
1 理论分析
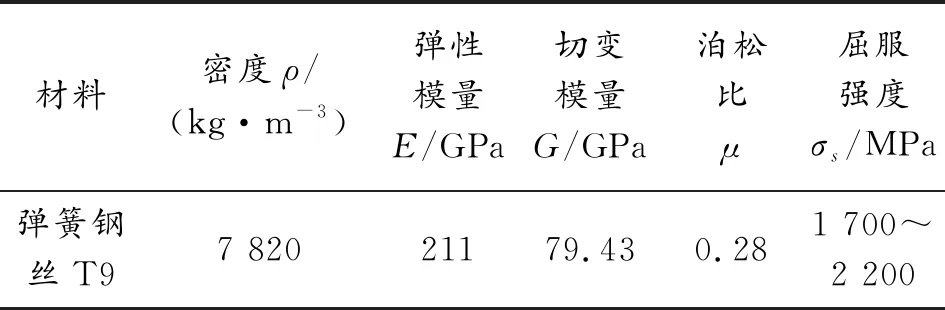
某引信后坐保险簧材料为特殊用途碳素弹簧钢丝,其主要设计参数如表1所列。已知该后坐保险簧为并紧磨端面弹簧,支撑圈数为1.5[4]。现以此为例研究引信圆柱螺旋压缩弹簧几何误差对抗力的影响。
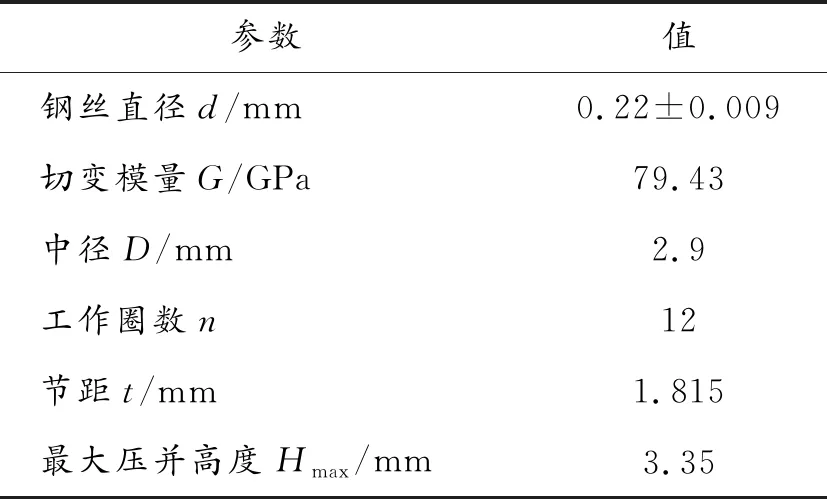
表1 某引信后坐保险簧的主要设计参数
1.1 端圈结构的影响
不考虑镀层厚度时的引信弹簧抗力公式[5]:
(1)
式中:λ为弹簧变形量,λ=H0-Hn;H0为弹簧自由高度;Hn为工作载荷时的高度。
端圈并紧结构的端圈与弹簧轴线垂直性好,且与支承座接触性好,具有较高的工作稳定性[6]。并紧弹簧在不同端圈结构下的自由高度H0[7]如表2所列。
由式(1)计算得后坐保险簧当检验高度hj=4 mm、在不同端圈结构下,抗力及相对基准条件(支撑圈1.5)的抗力变化率如表3所列。
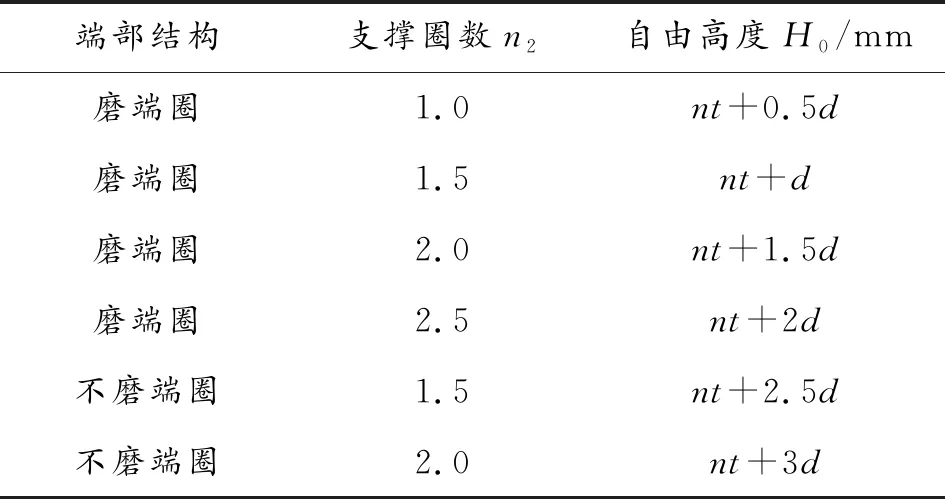
表2 并紧端圈弹簧不同端圈结构的弹簧自由高度

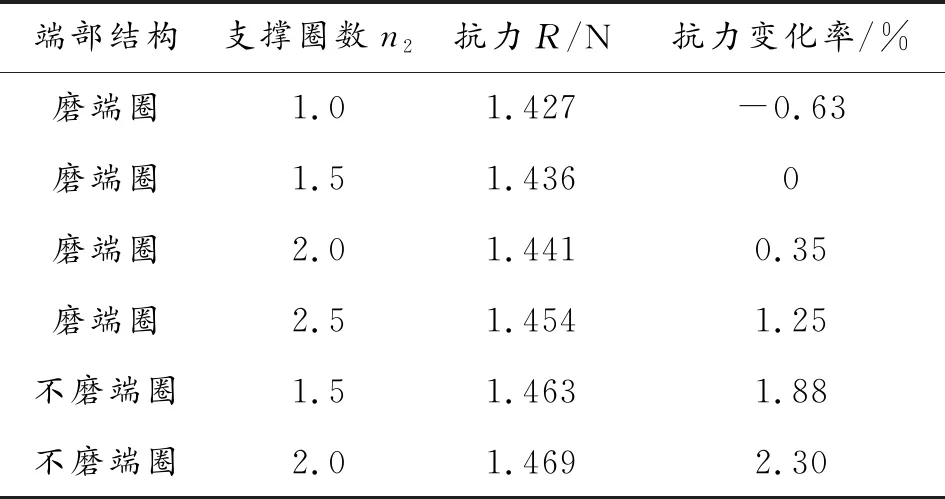
表3 并紧端圈的后坐保险簧在不同端圈结构下的抗力(对应检验高度4 mm)
由此可知并紧端圈弹簧在磨端圈与不磨端圈的情况下抗力都随着支撑圈的增加而增加。当支撑圈相同时,不磨端圈的抗力较大。由表3知n2≤2.5时抗力变化率小于3%。这表明并紧端圈弹簧的端圈结构(是否磨平及支撑圈数)对抗力虽然有影响,但影响较小,一般情况下可忽略。为了减小载荷偏心的影响,当旋绕比在3∶10之间时,弹簧端面最好磨平;在10∶15之间时,端面可磨也可不磨;大于15时就可不磨[7]。
1.2 弹簧钢丝截面的影响
1.2.1矩形截面
矩形截面材料弹簧的变形和应力计算公式推导很复杂,在此只引用简化计算公式[7]。
得载荷P与变形λ的关系式为
(2)
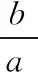
(3)
为了分析制造过程中由于加工误差使弹簧钢丝截面呈矩形时对抗力的影响,仍以并紧磨平的某圆柱形螺旋弹簧、支撑圈为1.5圈时的抗力R=1.430 N作为参考基准。抗力分析时,假定矩形的一条边与圆柱螺旋弹簧的直径相等,即b=d=0.22 mm,查文献[7]可知理论研究中采用的不同矩形截面弹簧的γ值均为5.2。由此按式(3)得不同矩形截面的弹簧抗力以及抗力变化率数值如表4所列。

表4 不同矩形截面弹簧的抗力以及抗力变化率(对应检验高度4 mm)
由表4知矩形截面弹簧的抗力随着边长的增大而增大。边长越大,则截面面积越大,抗力就显著增大,抗力变化率也显著变大。当矩形截面的长宽与标准弹簧截面的直径相等即a=b=d=0.22 mm时,面积增大了27.3%。
由表4知a=b=d=0.22 mm时,抗力变化率大于50%。因此加工制造时应尽可能避免弹簧钢丝截面出现矩形误差。
1.2.2椭圆形截面
椭圆形截面的圆柱螺旋弹簧抗力表达式为[7]:
(4)
式中:a′为椭圆的长径,b′为椭圆的短径。
(5)
此即为圆形截面圆柱螺旋弹簧的抗力表达式。抗力分析时,假定出不同长径和短径的椭圆形圆柱螺旋弹簧,其抗力和抗力变化率如表5所列。
表5第一行数据a=b,表示为圆形截面。由表5知椭圆形截面弹簧的抗力与圆形截面弹簧的抗力有明显区别,长径一定时,椭圆形截面弹簧的抗力随短径的增大而增大;短径一定时,椭圆形截面弹簧的抗力随长径的增大而增大。若椭圆截面面积比圆形截面面积大,则抗力会相应增大;若椭圆截面面积比圆形截面面积小,则抗力相应减小。
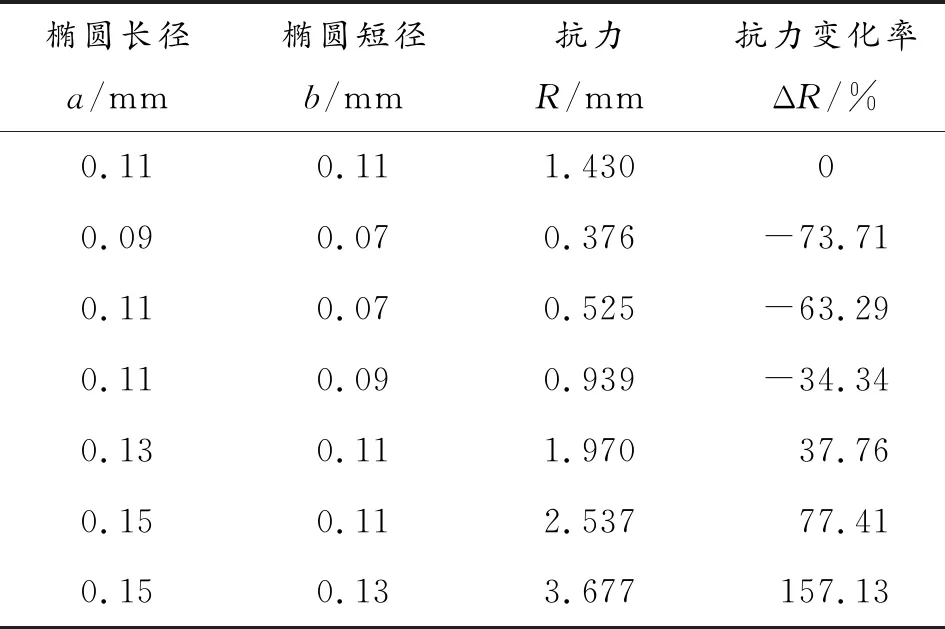
表5 不同椭圆截面弹簧的抗力以及抗力变化率(对应检验高度4 mm)
1.3 弹簧形状的影响
1.3.1圆锥形
由图3可知弹簧材料中心线的展开线为抛物线,螺旋线在xy底面上的投影为阿基米德螺旋线。由图3可看出,这种螺旋线的极角θ每增加2π,半径R就增大t·tanψ/2。这里ψ为弹簧的圆锥角。圆锥形弹簧的抗力为[7]:
(6)
圆锥角ψ与半径R1、R2的关系为:
(7)
取R1=1.45 mm时,结合式(11)和式(12),利用Matlab软件计算出不同圆锥角情况下的抗力大小R以及抗力变化率,如表6所列。

表6 不同圆锥角时弹簧的抗力以及抗力变化率(对应检验高度4 mm)
表6中圆锥角取正值表示R2>R1=1.45 mm,取负值表示R2 1.3.2中凹形和中凸形 中凹形和中凸形如图4所示。如以R2为最大弹簧圈半径、R1为中间最小弹簧圈半径,由于等螺旋角、等节距、等应力中凹形螺旋弹簧载荷与变形的公式各不相同,且较为复杂,所以为了方便分析,在此采用简化的公式计算。简化后不再区分等螺旋角、等节距与等应力等具体结构的中凹形螺旋弹簧抗力表达式为[7]: (8) 对于中凸形螺旋弹簧,如仍以R1表示两端最小工作弹簧圈半径,以R2表示中间最大弹簧圈半径,则引信中凸形圆柱螺旋弹簧的抗力表达式为[7]: (9) 取端部半径R2=1.45 mm即端部直径为2.9 mm时,利用Matlab软件计算出不同中凹形、中凸形引信弹簧抗力大小R以及相对于基准圆柱螺旋弹簧即中径D=2.9 mm的抗力变化率,如表7所列。 表7 不同中凹形、中凸形弹簧抗力及其变化率(对应检验高度4 mm) 由表7可知,当弹簧其他参数不变而中部凹陷时,弹簧抗力会明显增大,且抗力大小随起凹程度呈正比; 当弹簧其他参数不变而中部凸起时,则弹簧抗力减小,且抗力大小随凸起程度呈反比。 为了验证上述理论结果的正确性,采用有限元仿真软件workbench数值模拟。计算后坐保险簧作用至检验高度hj=4 mm时,不同几何误差对抗力产生的影响。弹簧由两压板相夹,其中一压板固定,另一压板顶面受力下压。后坐保险簧材料为特殊用途碳素弹簧钢丝,压板材料与后坐保险簧相同。仿真参数如表8所列。 表8 后坐保险簧和压板材料仿真参数[9] 为了防止压板变形影响弹簧自身变形,以致影响仿真结果,仿真时将压板的弹性模量E数值人为增大了9倍。 利用workbench仿真得到不同端圈结构下圆柱螺旋弹簧抗力及其变化,如表9所列。 在研究其他几何误差对圆柱螺旋弹簧抗力的影响时,为了仿真方便,未考虑弹簧并圈的影响。仿真得不考虑弹簧并圈时的结果如图5、图6所示。当弹簧压缩量λ=H0-hj=nt+d-hj=22-4=18 mm时,圆柱螺旋弹簧抗力值R=1.434 Ν。以R=1.434 Ν作为研究其他几何误差时的参考基准。 表9 不同端圈结构下圆柱螺旋弹簧的抗力仿真结果(对应检验高度4 mm) 利用SolidWorks分别绘制不同矩形截面、椭圆截面的螺旋弹簧模拟制造中可能出现几何误差后的弹簧钢丝横截面情况。这些几何误差对抗力影响的仿真结果如图7所示。 再利用SolidWorks分别绘制不同参数的圆锥形、中凹形、中凸形弹簧模拟制造中可能出现的中径几何误差,所用基本参数与理论推导中的相同,仿真结果如图8所示。上述仿真结果与理论推导结果基本一致。 考虑端圈结构对抗力的影响时,使弹簧工作圈数和节距不变,对比理论计算结果与仿真结果,可看出抗力变化率始终满足ΔR≤3%。而且对于并紧端圈弹簧,磨端圈与不磨端圈时的抗力都随着支撑圈的增加而增加。当支撑圈相同时,不磨端圈的弹簧抗力较大。 考虑弹簧钢丝截面对抗力的影响时,对比理论结果与仿真结果,可看出无论是制造误差使截面偏向椭圆形或矩形对圆柱形弹簧的抗力影响都非常大,如果截面面积增大,则抗力增大;如果截面面积减小,则抗力减小。 考虑簧丝截面形状对抗力影响时,对比理论计算结果与仿真结果,可看出对于圆锥形弹簧,若圆锥角取正值(即R2>R1=1.45 mm),则弹簧抗力减小,圆锥角越大,抗力越小。若圆锥角取负值(即R2 对于引信圆柱螺旋压缩弹簧,磨端圈与不磨端圈时的抗力都随支撑圈的增加而增加,端部结构对弹簧抗力影响较小,一般抗力变化率ΔR≤3%,即端圈结构(是否磨平及支撑圈数)对抗力的影响可以忽略。制造误差使弹簧截面呈椭圆形或矩形时都会严重影响弹簧抗力。截面面积增大,则抗力增大;截面面积减小,则抗力减小。弹簧呈锥形、中凹形、中凸形都会使抗力产生一定的变化。若制造误差使弹簧变粗(中径变大),则弹簧抗力减小;若制造误差使弹簧变细(中径变小),则弹簧抗力增大。制造过程中截面的误差和簧丝形状的误差对弹簧抗力的影响都比较大,因此制造过程中应尽可能避免出现此类误差。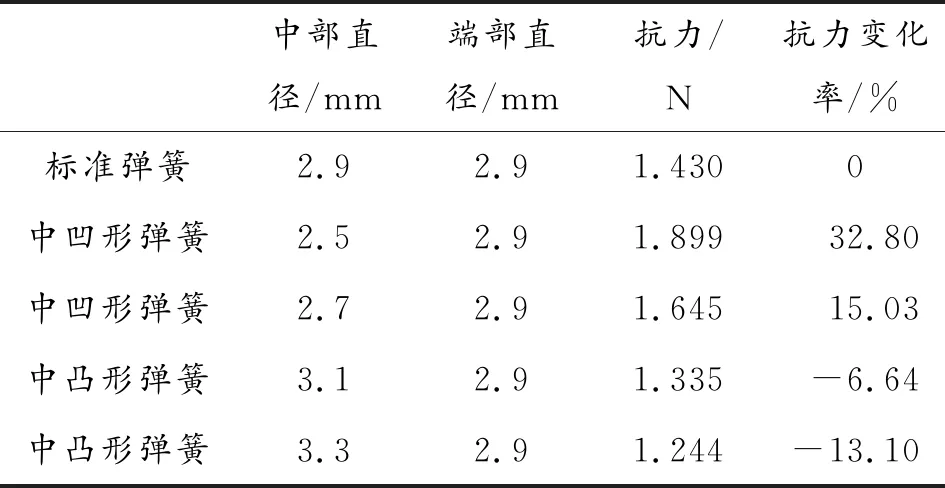
2 有限元仿真
3 结论
