部件柔性对含间隙多体系统动力特性的影响*

2016-11-23王铁成陈国平孙东阳

振动、测试与诊断 2016年3期

王铁成，陈国平，马方，孙东阳

(1.南京航空航天大学机械结构力学及控制国家重点实验室南京，210016)(2.盐城工业职业技术学院汽车工程学院盐城，224005) (3.重庆大学航空航天学院重庆，400044)

王铁成1，陈国平1，马方2，孙东阳3

构建了含有混合间隙的刚柔耦合多体系统动力学模型，研究了部件柔性对多体系统动力特性的影响。首先，建立了混合间隙碰撞力模型；然后，以曲柄滑块为研究对象，采用自然坐标法和绝对节点坐标法分别建立了刚性构件和柔性构件的动力学模型，通过时域和频域分析了连杆柔性对动力特性的影响。结果表明，柔性构件对间隙碰撞力有一定的缓冲作用，能缓冲碰撞的高频振动，而且柔性部件随着弹性模量的减小对高频响应的缓冲效果更加明显。

滑移副间隙; 旋转副间隙; 多体系统; 动力特性

引言

在机械系统中，由于加工、装配以及工作过程中的磨损，机械系统的运动副普遍存在间隙。间隙是部件间产生碰撞冲击的根源，碰撞冲击不仅使机构产生振动和噪声，而且降低系统的可靠性、寿命以及工作精度。随着机械系统向大型化、轻质和高速方向发展，部件柔性对系统有一定的影响，所以分析部件柔性对含间隙机械系统动力特性的影响是必要的。

在含间隙多体系统动力学研究方面，Flores[1-2]等做了大量的研究工作，包括含单个旋转副间隙系统以及含多个旋转副间隙的平面多体系统，提出了一种含有多个旋转副间隙的多体系统建模方法。针对柔性多体系统，Bauchau等[3]通过浮动坐标和有限元方法建立了含间隙柔性曲柄滑机构动力学模型，研究了间隙大小等因素对系统动力特性的影响，计算结果表明，多体系统部件柔性能够抑制碰撞力峰值。Muvengei等[4]将Lugre摩擦力引入计算模型中，研究了含两个旋转副间隙平面多刚体系统的动力学特性。郝雪清等[5]研究了不同运动副材料对间隙机构动力学特性的影响。谷勇霞等[6]对含多间隙帆板展开过程进行了研究，通过帆板展开过程中角速度的变化，分析了间隙碰撞对展开机构的稳定性的影响。Flores等[7-8]开展了含有移动副间隙的多体动力特性的研究。在高速运动过程中，柔性部件会产生动力刚化和大变形，应用传统有限元法建立的动力学模型已不能满足计算精度要求，甚至会在计算过程中出现难以收敛的问题。Shabana[9]以有限元和连续介质力学为基础，提出了采用绝对节点坐标建立柔性多体模型的理论，这种方法可以有效弥补传统有限元在计算多体系统高转速和大变形等情况下的缺陷。Tian等[10-11]基于绝对节点坐标方法分别研究了平面和空间含有单个间隙的柔性系统动力特性，研究发现，柔性系统模型中的间隙碰撞力比刚体系统要小。

笔者采用自然坐标法和绝对节点坐标法分别建立了刚性构件和柔性构件的动力学模型，以曲柄滑块机构为研究对象，通过时域和频域分析了连杆柔性对机构动力特性的影响。

1 间隙模型

1.1 旋转副间隙模型

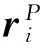
轴与轴承的中心距矢量和中心距分别表示为

(1)

(2)

轴与轴承接触点的单位法向量表示为

(3)

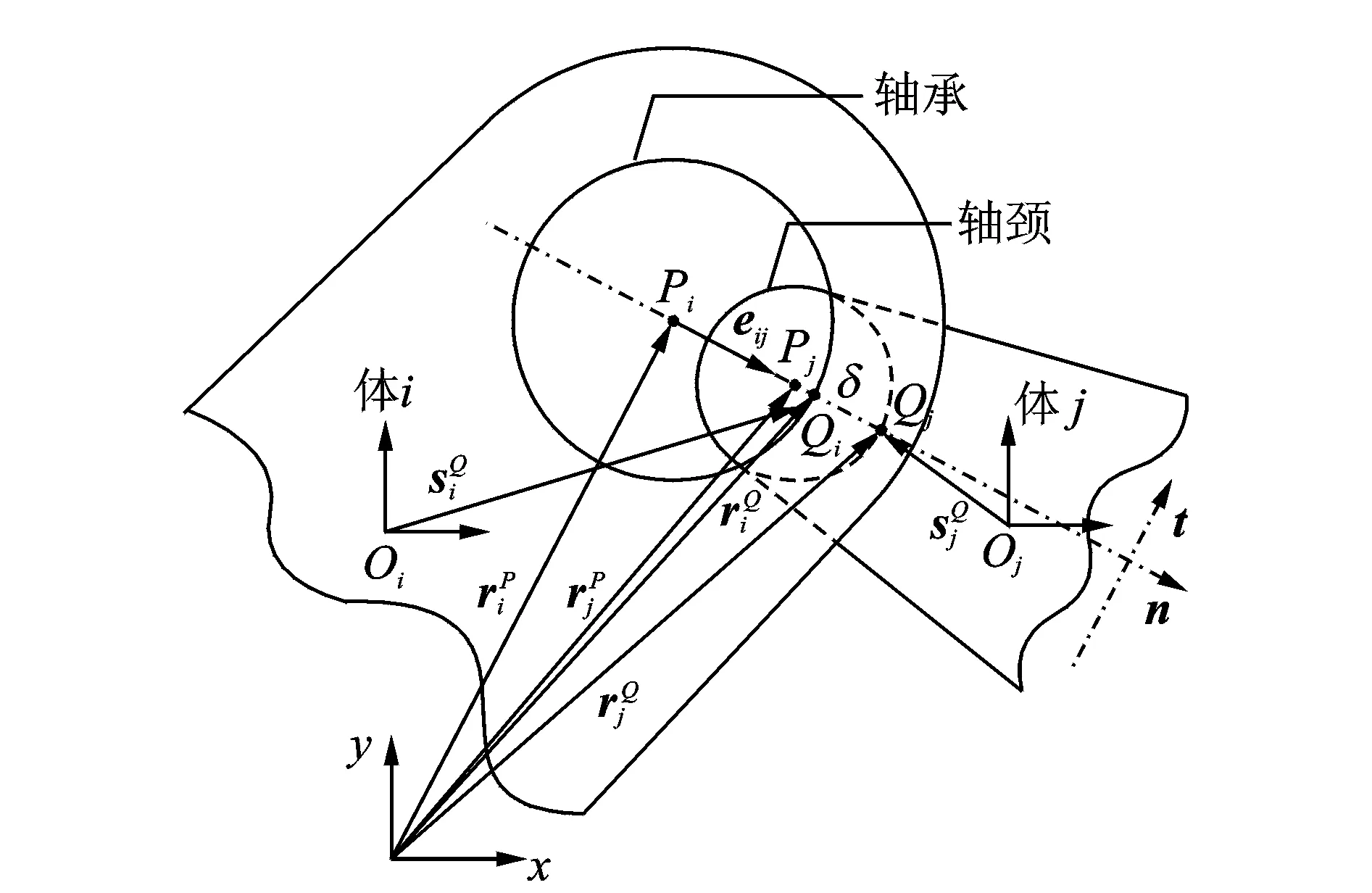
图1 旋转副间隙模型Fig.1 Revolute joint with clear

如图1所示，当轴和轴承发生碰撞时，其嵌入深度为

(4)

其中：C为间隙尺寸，其值等于轴承半径Ri与轴半径Rj之差，即C=Ri-Rj。

体i和体j的接触点Qi和Qj在全局坐标系中的矢量为

(5)

将式(5)对时间求导，得到接触点Qi和Qj的全局速度矢量

(6)

将接触点速度向接触面的法向和切向进行投影得到法向速度vN和切向速度vT，相对法向速度确定两个碰撞体是相对接近还是分离情况，相对切向速度确定两个体是否存在相对滑动。相对法向和切向速度可表示为

(7)

(8)

其中：向量n逆时针旋转90°得到切向量t。

当轴和轴承发生碰撞时，在碰撞面处就会产生碰撞力，将碰撞力分别向法向n和切向t投影，其中作用在碰撞点处的法向力fn可以表示为

fn=FNn

(9)

考虑到碰撞过程中的能量耗散，Lankarani等提出的连续碰撞模型[12]是应用非常广泛的一种碰撞力模型，该碰撞力模型可以表示为

(10)

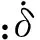
该碰撞模型只适用于恢复系数接近于1的情况。K为碰撞体的接触刚度系数，可表示为

(11)

参数hi和hj为

(12)

其中：vk为泊松比；Ek为弹性模量。

当碰撞过程中存在相对切向运动时，会在接触面上产生摩擦力，根据Ambrósio提出的库伦摩擦力法则[13]，切向力ft可表示为

ft=-cfcdFNvt/‖vt‖

(13)

其中：cf为摩擦因数；cd为动态校正系数。

(14)

将作用在体i和体j接触面上的法向力和切向力分别等效到体i的质心和体j的节点Oi和Oj，如图2所示，则作用在体i质心上的力和力矩分别为

fi=fn+ft

(15)

(16)

作用在体j节点上的力分别为

(17)

图2 碰撞点的力矢量Fig.2 Force vectors that act at the point of contact

1.2 移动铰间隙模型

含有间隙的移动副模型如图3所示，它是由滑块和导槽构成。滑块长为L，高为W，导槽的高为H，间隙大小为C，其表达式为

(18)

图3 移动副模型Fig.3 Translation joint model

如图4所示，移动副间隙中滑块与导槽有4种接触状态：a.自由运动状态，即无接触；b.滑块一角与导槽接触；c.侧面接触；d.对角同时接触导槽。

为建立移动副间隙的受力分析模型，将与体j固连的局部坐标系中由P点指向Q点的单位矢量t′，向惯性坐标系投影可以得到

t=Hjt′

(19)

其中：Hj为体j固连坐标系到总体坐标系的转换阵。

对体j和体i上的任意点G，用总体坐标系中的坐标可表示为

(20)

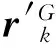
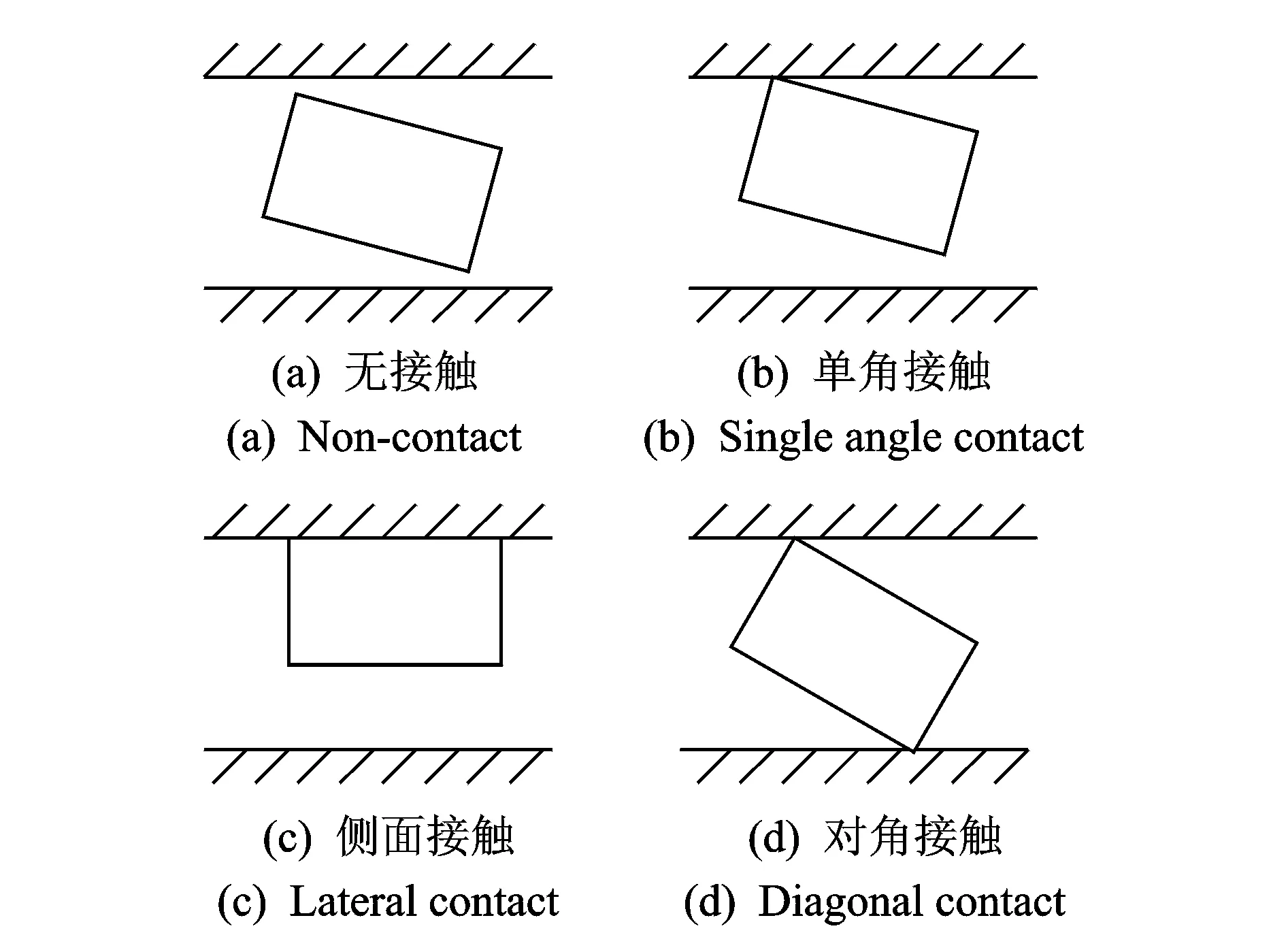
图4 移动铰4种运动状态Fig.4 Four motion state of translation

如图5所示，导槽PQ边上离滑块点Ai距离最近的点Aj在总体坐标中的位置矢量可表示为

(21)

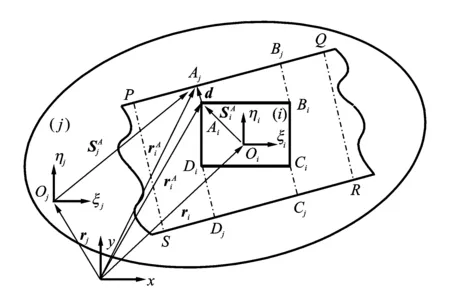
图5 移动铰碰转点矢量Fig.5 The collision point vector of translation joint

连接滑块上点Ai到导槽上点Aj的矢量为

(22)

判断d的方向与导槽表面的法向方向n是否一致，可由单位向量t顺时针方向旋转90°得到。则n可表示为

(23)

滑块和导槽发生碰撞并有渗透时，满足下式条件

dTn<0

(24)

根据Lankarani提出的两平面间线性接触力模型[14]，滑块与导槽的碰撞力可表示为

(25)

其中：Ks为接触刚度。

(26)

其中：a为矩形接触面周长的一半；hi和hj可由式(12)计算得到。

将滑块与导槽的碰撞力分别向碰撞面的法向和切向投影，则法向碰撞力fn为

fn=FNn

(27)

作用在滑块上的摩擦力ft同样可由式(13)给出。

如图6所示，将作用在接触面上的碰撞力等效到滑块i质心上，则力和力矩分别表示为

fi=fn+ft

(28)

(29)

作用在导槽体j质心上的力和力矩分别为

(30)

(31)

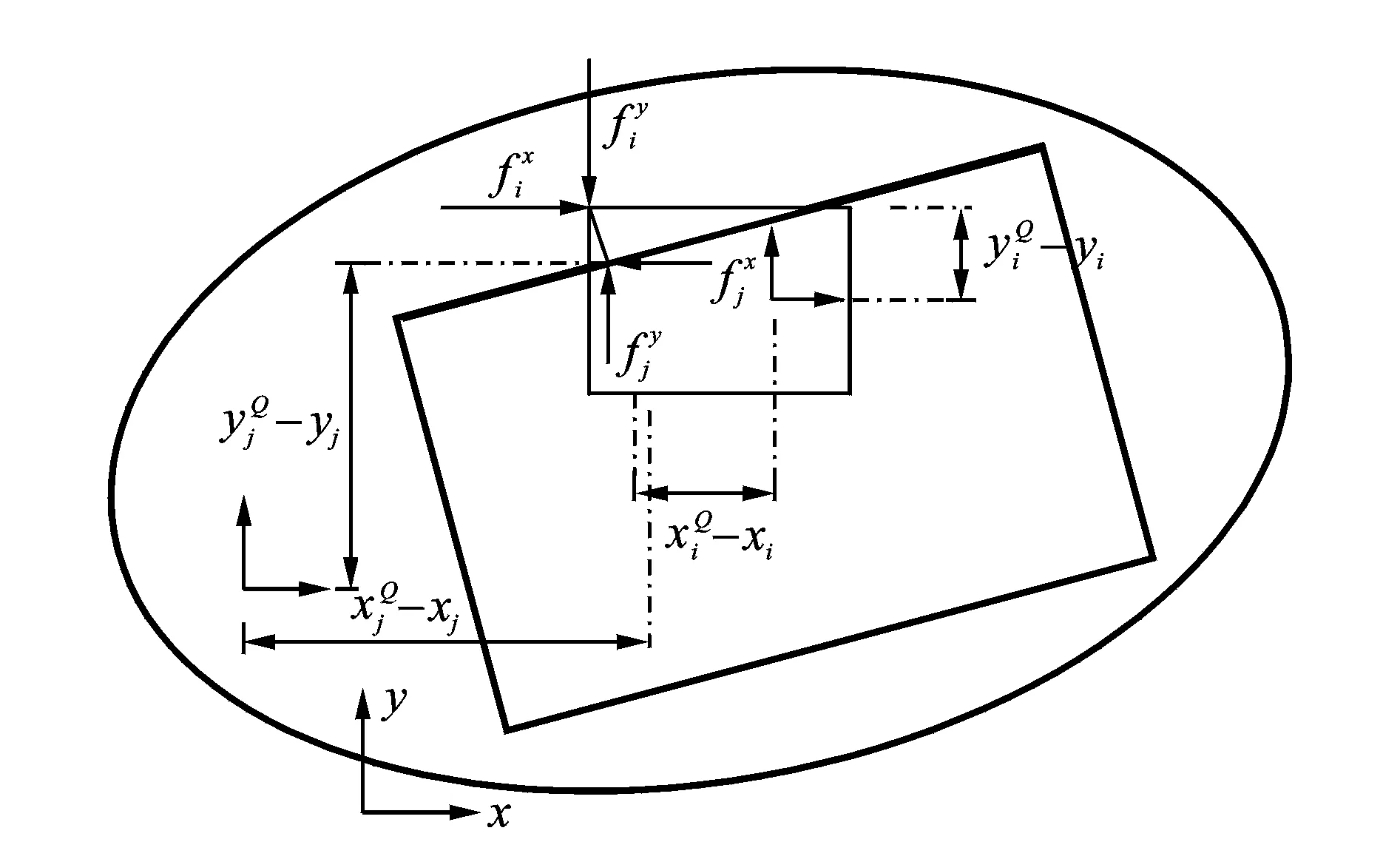
图6 移动铰碰撞力矢量Fig.6 The collision force vector of translation joint

2 绝对节点坐标法与动力学控制方程

2.1 绝对节点坐标法

基于绝对节点坐标法的一维两节点梁单元如图7所示，单元上任意点的位置矢量可表示为

(32)

其中:S为定义在总体坐标系上的形函数。

(33)

其中：s1=1-3ξ2+2ξ3；s2=ξ-3ξ2+2ξ3；s3=3ξ2-2ξ3；s4=l(ξ3-ξ2)；ξ=x/l；e为单元节点坐标。

e[7]表示为

(34)

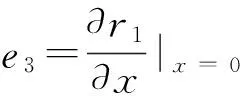
图7 平面梁单元Fig.7 Plane beam element

根据式(33)，单元的动能可表示为

(35)

其中：Me=∫ρSTSdV，为单元的常数质量阵；ρ和V分别为材料的密度和单元的体积。

基于虚功原理建立单元的动力学方程

(36)

其中：Qe为单元受到的广义外力；Qk为单元广义弹性力。

单元广义弹性力由单元应变能对单元坐标求偏导获得

(37)

其中：Ue为单元的总应变能。

根据连续介质力学理论，单元的总应变能包含弯曲应变能Uel和轴向拉伸应变能Uet，可表示为

(38)

其中：εi和κ分别为单元应变和曲率。

含约束柔性体k的动力学方程为

(39)

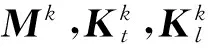
其中：Be为布尔矩阵。

2.2 动力学控制方程

基于拉格朗日方法，建立了含约束的刚柔耦合多体系统动力学方程

(40)

式(40)为微分-代数方程，在数值求解过程中有可能出现违约。这里采用Baumgarte违约修正法来抑制求解过程中误差的增长，则式(40)可以进一步表示为

(41)

其中：α，β为稳定性系数，它们的取值范围在1～50之间。

3 算例分析

以曲柄滑块机构为例，该曲柄滑块机构由地面1、曲柄2、连杆3和滑块4组成，如图8所示，其相关的结构参数见表1。

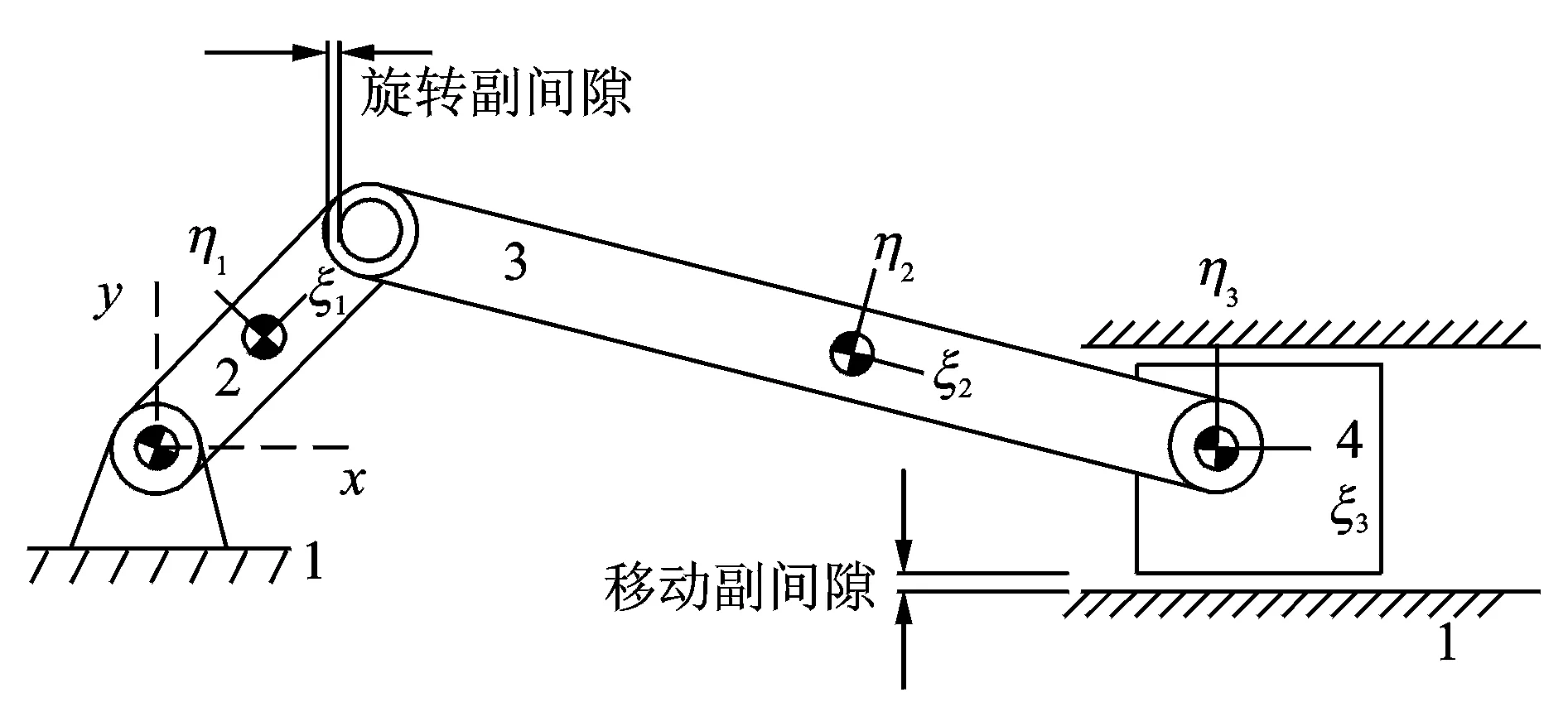
图8 曲柄滑块示意图Fig.8 Slide-crank mechanism

Tab.1 Geometric and intertia properties of slide-crank mechanism

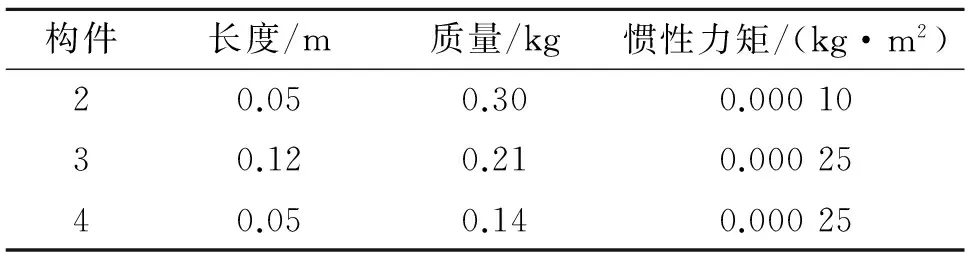
构件长度/m质量/kg惯性力矩/(kg·m2)20.050.300.0001030.120.210.0002540.050.140.00025

曲柄滑块间隙属性与运动副参数见表2。在刚柔耦合模型中，曲柄和连杆分别采用自然坐标法和绝对节点坐标法建模。连杆离散为6个一维二节点绝对节点坐标梁单元。为对比连杆为刚性的情况，采用自然坐标法建立了曲柄滑块机构的刚性模型。通过施加外力矩使曲柄以5 kr/min的恒定角速度转动，并带动连杆运动。初始时刻，曲柄和连杆都处于水平位置。本研究分析的模型中，设定旋转副间隙大小和移动副间隙大小是相同的，间隙改变指的是两种运动副间隙同时改变且相同。

表2 曲柄滑块机构运动副参数

Tab.2 Parameters used in the dynamic simulation of the slide-crank mechanism with clearance joins

移动副旋转副滑块长度/mm滑块高度/mm弹性模量/GPa泊松比轴半径/mm弹性模量/GPa泊松比5.08.02070.310.02070.3

为研究部件柔性对碰撞力的影响，首先分析了无间隙、间隙C=0.05和C=0.2 mm时，刚性曲柄滑块机构的曲柄力矩。三种情况下的曲柄力矩的时域曲线见图9，有间隙时的频率成分分布见图10。由图9可知，无间隙时，曲柄力矩的峰值在140 Nm左右，而有间隙时，曲柄力矩曲线有很多毛刺，这主要是运动副部件的频繁接触碰撞产生的，可见间隙明显影响了机械系统的动力学特性。可以发现，间隙从0.05mm增大到0.2mm后，曲柄力矩波动峰值有明显增大，从200Nm左右增大到400Nm左右。由图10可以看出，间隙增大后，在2 kHz～3 kHz的范围内仍为高频成分的主要区间，但高频成分的峰值有明显的增大。

图9 不同间隙时的曲柄力矩曲线Fig.9 Crank moment for the different clearance

当间隙C=0.05 mm，连杆的弹性模量E为2，6，20和80 GPa时的曲柄力矩结果如图11所示。可以发现，曲柄力矩曲线仍有很多毛刺，并且曲柄力矩个别峰值已达到200 Nm。为了分析间隙碰撞对驱动力矩高频和低频响应的影响，图12给出了曲柄力矩频率分布。由图可以发现，随着连杆弹性模量的降低，曲柄力矩响应的高频成分也相应有所降低。当E=80 GPa时，高频成分主要集中在2～2.5 kHz内；当E=20 GPa时，高频成分集中在1 kHz～2 kHz以内；当E=6 GPa时，高频成分集中在1 kHz左右;当E=2 GPa时，高频成分集中500 Hz左右。

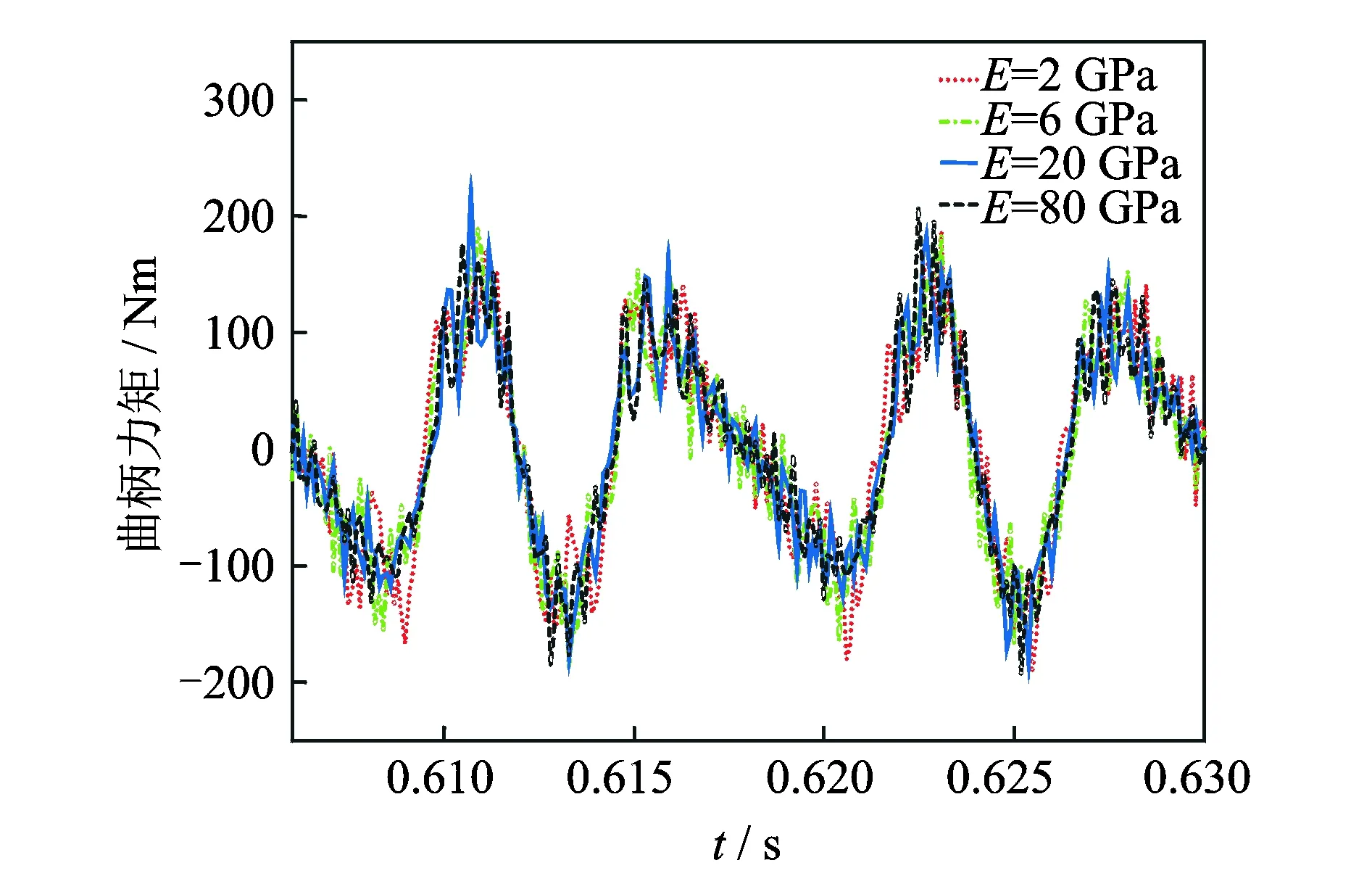
图11 不同弹性模量的曲柄力矩曲线(C=0.05 mm)Fig.11 Crank moment for the different modulus of elasticity(C=0.05 mm)

图12 不同弹性模量的曲柄力矩频域分布(C=0.05 mm)Fig.12 Frequency distribution of crank moment for the different modulus of elasticity(C=0.05 mm)

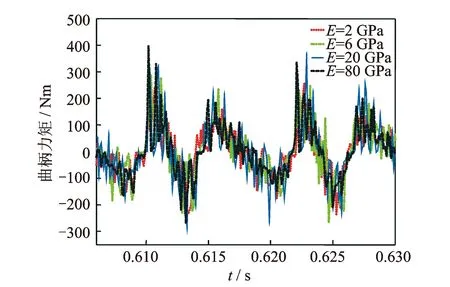
图13 不同弹性模量的曲柄力矩曲线(C=0.2 mm)Fig.13 Crank moment for the different modulus of elasticity(C=0.2 mm)

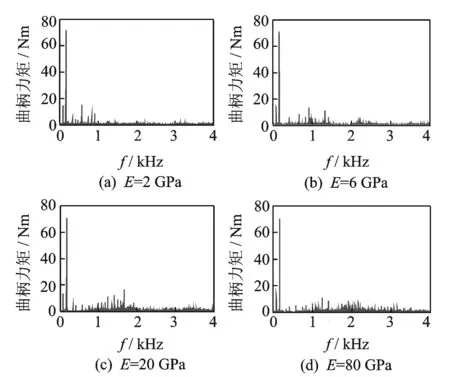
图14 不同弹性模量的曲柄力矩频域分布(C=0.2 mm)Fig.14 Frequency distribution of crank moment for the different modulus of elasticity(C=0.2 mm)

当间隙C=0.2 mm时，曲柄力矩时域曲线和频率分布分别如图13和图14所示。由图13可以发现，间隙碰撞对曲柄力矩的影响更加明显，此时从频率分布图上看，随着弹性模量的降低，高频成分也随着降低。由此可见,部件柔性能够缓冲含间隙机械系统的高频冲击响应。

4 结束语

笔者以曲柄滑块机构为研究对象，建立同时含有移动副间隙和旋转副间隙的刚柔耦合动力学计算模型，在时域和频域中分析连杆柔性对曲柄力矩的影响。计算结果表明，连杆的柔性对间隙碰撞有一定的缓冲作用，对高频振动也有缓冲作用，这种作用随着连杆弹性模量的减小而更加明显。所提出的含混合间隙刚柔建模方法以及通过频率对曲柄力矩的分析，为含有多间隙的高速机构等机械系统的动力特性分析提供了一定的思路，有一定的工程实用价值。

[1] Flores P, Ambrósio J, Claro J P. Dynamic analysis for planar multibody mechanical systems with lubricated joints[J]. Nonlinear Dynamics,2004,12:47-74.

[2] Flores P, Lankarani M H. Dynamic response of multibody systems with multiple clearance joints[J]. Journal of Computational and Nonlinear Dynamics, 2012(7):31001-31003.

[3] Bauchau O A, Rodriguez J. Modeling of joints with clearance in flexible multibody systems[J]. International Journal of Solids and Structure, 2002(39):41-63.

[4] Muvengei O, Kihiu J, Ikua B. Dynamic analysis of planar multi-body systems with Lugre friction at differently located revolute clearance joints[J]. Multibody System Dynamics, 2012,28(28):369-393.

[5] 郝雪清,陈江义.不同运动副材料对间隙机构动力学特性的影响[J].振动与冲击,2012,31(12):19-21.

Hao Xueqing，Chen Jiangyi.Effects of different materials in joints on dynamic characteristics of a mechanism with clearance[J]. Joural of Vibration and Shock,2010,31(12):19-21. (in Chinese)

[6] 谷勇霞,杨天夫,郭峰.考虑多间隙的帆板式展开机构动力学分析[J].振动、测试与诊断,2015,35(1):36-40.

Gu Yongxia, Yang Tianfu, Guo Feng. Dynamic performance of a solar array deployable mechanism with multiple clearances[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(1):36-40. (in Chinese)

[7] Flores P, Ambrósio J. Revolute joints with clearance in multibody systems[J]. Computers & Structures, 2004,82:1359-1369.

[8] Flores P, Ambrósio J. Translational joints with clearance in rigid multi-body system[J]. Journal of Computational and Nonlinear Dynamics, 2008,3(1):112-113.

[9] Shabana A. An absolute nodal coordinates formulation for the large rotation and deformation analysis of flexible bodies[D]. Chicago: University of Illionis at Chicago, 1996.

[10]Tian Q, Zhang Y, Chen L. Dynamics of spatial flexible multibody systems with clearance and lubricated spherical joints[J]. Computers & Structures, 2009,87:913-929.

[11]Tian Q, Zhang Y, Chen L. Simulation of planar flexible multibody systems with clearance and lubricated revolute joints[J]. Nonlinear Dynamics, 2010,60:489-511.

[12]Lankarani H M. A contact force model with hysteresis damping for impact analysis of multibody systems[J]. Journal of Mechanical Design, 1990,112:369-376.

[13]Ambrósio J A C. Impact of rigid and flexible multibody systems: deformation description and contact models[M]. Netherlands: Springer, 2002:57-58.

[14]Lankarani H M. Canonical equations of motion and estimation of paramrters in analysis of impact probems[D]. Tucson: University of Arizona, 1988.