基于BFGS摄动法的固定梁损伤检测*

黄振南, 胡 彪

(1.兰州理工大学机电工程学院 兰州，730050) (2.电子科技大学机械电子工程学院 成都，611731)



基于BFGS摄动法的固定梁损伤检测*

黄振南1, 胡 彪2

(1.兰州理工大学机电工程学院 兰州，730050) (2.电子科技大学机械电子工程学院 成都，611731)

运用损伤结构的特征值问题,建立拟牛顿法的BFGS优化摄动方法来检测固定梁的损伤情况。 多单元两端固定梁的损伤位置与程度, 可以从首几对振动模态在数次迭代內准確获取。首先，摄动展开损伤结构的刚度矩阵、特征值和特征向量, 并代入损伤结构的特征值方程；然后，集合p阶的弹性模量摄动项,以显式直接推导特征参数的p阶摄动系数；最后，把系数代入摄动方程，对于多个弹性模量进行BFGS拟牛顿优化迭代, 其目标函数由摄动方程剩余项的总和产生。 使用两端固定梁的有限元模型,五单元至九单元梁的损伤检测验证了该方法在有限模态参数与减少自由度模型的有效性。在终止准则方面，使用了d-模与t-模比较不同迭代阶段的收敛性, 并精确地在0.06～0.001弹性模量误差內检测了小至大损伤的各个单元号及其损伤程度。

BFGS摄动法；两端固定梁；损伤检测；拟牛顿优化

引 言

各种敏感度分析在过去几十年得到了快速的发展。Fox等[1]在考虑结构设计变量的基础上，计算出特征参数的变化率。Rogers[2]将他们的研究发展到非对称特征值问题中。Nelson[3]分析了对称和非对称多系统的特征向量简化的导出式。Wanxie等[4]采用稳态雷利商对于多模态特征值作出二阶敏感性分析。Wicher等[5]确定了结构系统在频率域的二阶敏感度矩阵。Wilkinson[6]制定了特征值问题的摄动理论。Brandon[7]以摄动分析计算出特征值和特征向量的二阶摄动项。Ryland等[8]发展了二阶摄动法，可以计算质量和刚度矩阵发生小摄动时的特征参数变化。文献[9-10]推导出扭矩耦合建筑问题的二阶摄动解法。大多数的摄动分析只涉及单变量，而Stahara[11]提出了一阶多变量摄动程序来优化设计涡轮叶片的轮廓。然而, 涉及交叉项的多变量摄动分析尚未显示在文献中。

各种振动方法中，可以使用特征值、特征向量或特征向量曲率[12-13]作为优化目标。这项研究采用了特征向量和特征值构造优化目标函数。多变量p阶的摄动法得到了发展，把弹性模量的变化设为摄动变量，令相同阶的弹性模量摄动项在各特征向量和特征值系数中相等，特征参数的各阶摄动项就可渐次得到，并采用BFGS拟牛顿法进行结构的弹性模量优化。从广义的结果分析，两端固定梁的有限元模型验证了算法的收敛性与有效性。

1 BFGS摄动法的理论基础

由于在一个损伤结构中惯性改变造成的影响非常小，往往只考虑损伤中造成的弹性模量改变。考虑一个nφ维自由度、线性、时间不变、不同特征值的自伴系统。未损伤结构的弹性模量为Ghi(i=1,2,...，m)，其中m为弹性模量的数量，以弹性模量的减少来描述结构损伤。在每次迭代前损伤结构的弹性模量为Gi(i=1,2,...，m)，而取决于Gi的线性刚度矩阵为K=K(G)，其中G=[G1,G2,...，Gm]T。带有弹性模量Gi的结构的特征值问题为

(1)

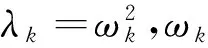
式(1)中的标准化特征向量也满足以下正交关系

(2)

其中:1≤u≤N;δku为克罗內克函数。

(3)

这几个变量可通过摄动方程得到，其中刚度矩阵的一阶摄动式为

(4)

其中：δGi=Gdi-Gi(i=1,2,...,m)为弹性模量的摄动量。

考虑到K为Gi的线性函数，其Gi更高阶的导出式就被消去，因此一个连续结构的有限元整体刚度矩阵也会满足式(4)。损伤结构的k级特征值和质量标准化的特征向量可通过摄动式与λk和φk相关联

(5)

(6)

所形成的是特征值系数和特征向量的各阶交叉项,下标括号中的数字代表项的阶数。验算这些交叉项，对于任何p≥1有

(7)

(8)

集合式(8)中的p阶变量δGiδGj…δGsδGt得到式(5)、式(6)中的p阶摄动项

(9)

(10)

在式(9)前乘以(φk)T,并利用式(1)、式(2)与式(10)得

(11)

p阶特征值的摄动系数是从式(5)和式(11)中得到,它们各自依赖于p阶以下的特征值和特征向量。

在式(9) 前乘以 (φv)T，其中1≤v≤N且v≠k，利用式(1)、式(2)和式(10) 得

(12)

(13)

(14)

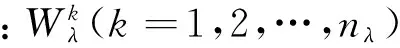
整个优化过程使J极小化, 并采用以下拟牛顿迭代格式

(15)

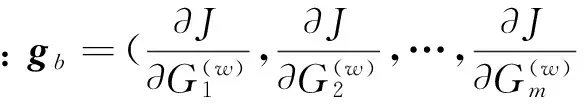
(16)

(17)

其中:wdn为达到d-模准则的最少迭代次数。

另一个t-模终止准则是：当wtn次与损伤权重标准化特征参数差模，小于初始与损伤特征参数差模的tn百分比

(18)

其中:wtn为达到t-模准则的最少迭代次数。

2 两端固定梁的损伤检测

图1 两端固定梁的有限元模型Fig.1 Finite element model of fixed-fixed beam

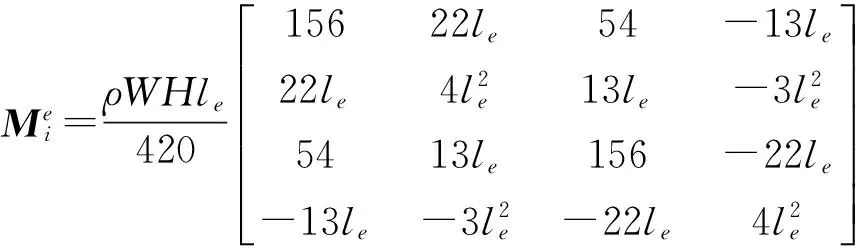
(19)

刚度矩阵为

(20)

集合过程采用自动化程序，可导出2(Ne+1)×2(Ne+1)维的整体系统矩阵。约束边界两个节点的横向位移和转角变量为零，可得到N×N维的系统矩阵，其中N=2(Ne-1)为系统自由度，而系统的位移向量(包括所有无约束的节点)为[V2,θ2,V3,θ3,…,VNe,θNe]T。现在使用摄动法的计算机程序来检测例案5o1_rs 至9o2_rl的五、七和九单元梁受到小、中、大三种程度损伤时的弹性模量摄动量。

2.1 五单元梁的损伤检测

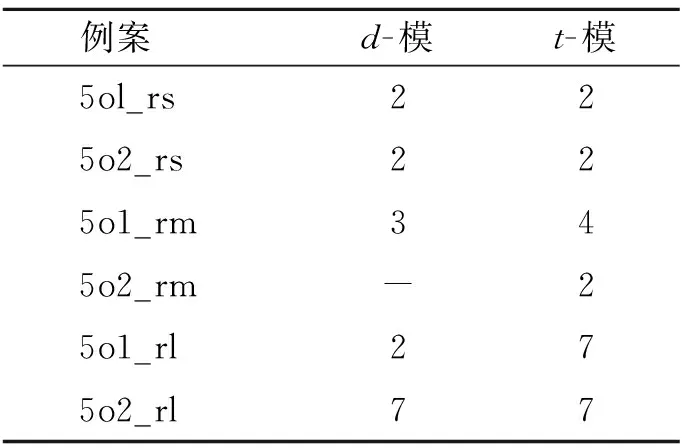
首先以一阶算法来检测5个单元固定梁的中损伤[15]，运用首五对模态参数,即nλ=nφ=5，其t-模值从笫1次迭代的9.72×10-1迅速下降至笫2次的8.27×10-2，达到10-6的t-模准则(tn=10-4)。从弹性模量的百分比误差曲面(见图2)，各单元的弹性模量在笫2次迭代扭转, 其误差范围在-12.8% ～3.62%, 然后平稳地收敛在极小误差向量Gdp={-0.006,0.006,0.000,0.031,0.013}%。总结所有五单元例案，得到1%d-模的收敛见表1。在小损伤的例案中，一阶与二阶算法的收敛情况是相等的；中损伤的例案，d-模的准则还未达到，t-模已达到，二阶算法的收敛速度较快；大损伤检测，一阶算法需要达到d-模的次数较少，因此收敛速度较慢。分析表1的t-模, 在小损伤检测中，两种算法是一样的；在中损伤检测，二阶算法相对更有效，对应d-模的情况；在大损伤检测，两种算法拥有相同的收敛性。

表1 五单元梁损伤检测的收敛次数

Tab.1 Convergence number of five element beam damage detection

例案d-模t-模5ol_rs225o2_rs225o1_rm345o2_rm-25o1_rl275o2_rl77

图2 例案5o2_rm 五单元梁二阶中损伤的检测误差Fig.2 Case 5o2_rm minimum error of five element beam second order medium damage detection

2.2 七单元梁与九单元梁的损伤检测

现在把单元数量增加至7个与9个，从表2显示七单元梁大损伤中，二阶算法的1% d-模收敛速度较一阶算法快, 迭代次数分别是2次与3次。在10-6t-模准则，二阶算法(6次)的收敛速度比一阶(7次)稍快。运用二阶的d-模曲线(见图3)，其值从笫1次迭代的13.5迅速下降至笫2次迭代的1.31，然后收敛到4.44×10-2。分析2阶的弹性模量的百分比误差曲面，所有单元在笫2次迭代下降到 -33.2% ～16.1%的范围。从笫3次迭代开始, 它们严格地收敛到笫7次的极小误差向量 Gdp={0.001,0.014,-0.004,-0.011,0.010,-0.098,0.000}%。

图3 例案7o2_rl七单元梁二阶大损伤的d-模曲Fig.3 Case 7o2_rl d-norm curve of seven element beam second order large damage detection

Tab.2 Convergence number of seven and nine element beams damage detection

例案d-模t-模7o1_rl277o2_r1469o1_rs229o2_rs22

至于九单元的小损伤，两种算法的d-模准则同时在笫2次迭代收敛。另外，在t-模准则，一阶算法(3次) 的收敛速度比二阶的(2次) 较慢。分析二阶算法，弹性模量的误差在笫1次迭代下降到-0.972%～0.253%范围以內，然后在笫2次迭代，有效地收敛到极小误差向量

Gdp={-0.045,-0.057,-0.034,-0.049,-0.058,-0.051,-0.042,-0.048,-0.049}%

3 结束语

基于BFGS优化的p阶摄动法已直接推导出来, 准确检测了固定梁的结构损伤。使用首五对模态参数, 在五单元的固定梁，检测初期的收敛性随着损伤的程度增加，二阶算法达到精度的速度比一阶更快，在迭代末期，两种算法效率基本一样。对于七单元梁的大损伤，在d-模准则一阶算法的收敛性比较强，在t-模准则二阶算法达到精度的速度较快，极小误差值在0.1%以內。对于九单元梁的小损伤，在初期两种算法具有相同的收敛性，在迭代末期一阶算法达到精度的速度较慢，其极小误差值在0.06%以內。所以随着单元数量的增加，一阶算法在d-模准则相对有效，而二阶算法在t-模准则更有效。

[1] Fox R L, Kapoor M P. Rate of change of eigenvalues and eigenvectors[J]. American Institute of Aeronautics and Astronautics Journal, 1968, 6(12): 2426-2428.

[2] Rogers L C. Derivatives of eigenvalues and eigenvectors[J]. American Institute of Aeronautics and Astronautics Journal, 1970, 8(5): 943-944.

[3] Nelson R B. Simplified calculation of eigenvector derivatives[J]. American Institute of Aeronautics and Astronautics Journal, 1976, 14:1201-1205.

[4] Wanxie Z, Gengdong C. Second-order sensitivity analysis of multi-modal eigenvalues and related optimization techniques[J]. Journal of Structural Mechanics, 1986, 14(4): 421-436.

[5] Wicher J, Nalecz A G. Second order sensitivity analysis of lumped mechanical systems in the frequency domain[J]. International Journal for Numerical Methods in Engineering, 1987, 24: 2357-2366.

[6] Wilkinson J H. The algebraic eigenvalue problem[M]. Oxford: Clarendon Press, 1965: 62-71.

[7] Brandon J A. Derivation and significance of second-order modal design sensitivities[J]. American Institute of Aeronautics and Astronautics Journal, 1983, 22(5): 723-724.

[8] Ryland G, Meirovitch L. Response of vibrating systems with perturbed parameters[J]. AIAA Journal of Guidance and Control, 1980, 3: 298-303.

[9] Kan C L, Chopra A K. Elastic earthquake analysis of torsionally coupled multistorey buildings[J]. Earthquake Engineering and Structural Mechanics, 1977, 5: 395-412.

[10]Tsicnias T G, Hutchinson G L. A note on the perturbation analysis of the mode shapes of torsionally coupled buildings[J]. Earthquake Engineering and Structural Dynamics, 1982, 10: 171-174.

[11]Stahara S S. Development of a turbomachinery design optimization procedure using a multiple-parameter nonlinear perturbation method[R]. USA: NASA Scientific and Technical Information Branch, 1984.

[12]孙增寿,韩建刚,任伟新. 基于曲率模态和小波变换的结构损伤识别方法[J]. 振动、测试与诊断, 2005, 25(4):263-268.

Sun Zengshou, Han Jiangang, Ren Weixin. Structural damages identification based on curvature mode and wavelet transform[J]. Journal of Vibration, Measurement & Diagnosis, 2005, 25(4):263-268.(in Chinese)

[13]李国强,梁远森. 振型曲率在板类结构动力检测中的应用[J].振动、测试与诊断, 2004, 24(2):111-117.

Li Guoqiang, Liang Yuansen. Dynamic damage detection of plate-like structure using curvature mode shapes[J]. Journal of Vibration, Measurement & Diagnosis, 2004, 24(2):111-117.(in Chinese)

[14]Patalambros P Y, Wilde D J. Principles of optimal design- modeling and computation, second edition[M]. Cambridge: Cambridge University Press, 2000:338-343.

[15]胡彪. 运用摄动原理更新工程梁的结构系数[D]. 成都: 电子科技大学, 2009.

10.16450/j.cnki.issn.1004-6801.2016.03.021

*国家自然科学基金资助项目(50905028，51275554)

2014-05-17；

2015-12-23

TH113.1

黃振南，男，1965年12月生，教授、硕士生导师。曾发表《Perturbed eigenvalue problem with the davidon-fletcher-powell quasi-Newton approach for damage detection of fixed-fixed beam》(《Mathematics and Mechanics of Solids》 2011,Vol.16,No.2)等论文。

E-mail: znhuang@lut.cn