杆系结构鲁棒性应变能敏感度分析及试验*

2016-11-23刘国光武志玮

振动、测试与诊断 2016年3期

关键词：星型压杆杆件

刘国光，武志玮，刘鑫

(中国民航大学机场学院天津，300300)

杆系结构鲁棒性应变能敏感度分析及试验*

刘国光，武志玮，刘鑫

(中国民航大学机场学院天津，300300)

为研究结构鲁棒性动态分析方法，进行了理论分析、数值模拟和破坏性模型试验。结合平面悬臂桁架和六角星型穹顶算例，利用应变能敏感度法分析了杆系结构鲁棒性。基于杆件移除法讨论了结构应变能和应变能敏感度对结构破坏特征的影响，并同鲁棒性应力变化率评价法进行了对比。结果表明：应变能敏感度法能动态地反映杆系结构鲁棒性变化、预测结构稳定极限荷载、识别结构破坏模态及评价杆件易损性;尽管支座压杆、环向拉杆对应变能敏感度的影响比中心压杆小，但可能引起结构整体倾覆和中心压杆强度破坏；工程应用中应在杆件重要性分析和结构破坏模态识别基础上采用应变能敏感度法评价结构鲁棒性。

空间结构；鲁棒性；杆系结构；应变能敏感度；六角星型穹顶

引言

鲁棒性是结构在偶然事件中发生局部损伤而不产生与损伤起因不相称破坏的能力[1]，结构鲁棒性分析可用于结构抗连续倒塌设计及灾后结构安全性能评价等，针对结构鲁棒性的量化研究理论是当前的研究热点，其研究方法主要分为基于结构属性和基于结构性能两类[2]，主要目的在于预测结构抗破坏能力。

为了合理预测结构性能，同时提高计算效率，文献[3-7]分别从量化、概率分析、向量式结构力学有限质点法、弹性冗余度理论和结构易损性理论等方面分析了结构鲁棒性，并通过有限元结构算例分析加以验证。文献[8-9]基于能量观点研究了结构安全性与鲁棒性的关系。文献[10]利用能量流动网络，通过折减杆件刚度模拟结构构件受到的损伤来分析结构鲁棒性。文献[11]采用局部应变能大小考察单根杆件初始破坏对整体结构倒塌的中间传递作用，指出在结构连续倒塌过程中起到传递作用的杆件也属于关键杆件。文献[12-13]针对杆系结构提出了应变能敏感度理论，通过增加和减少单元优化杆系结构形态，提高结构承载效率。文献[14]分析了六角星型穹顶结构的易损性及杆件在荷载作用下的应力，找到了结构多种失效模式。在进行鲁棒性分析中，结构响应同单根杆件破坏次序密切相关，因此多采用杆件移除法判断结构破坏模式[15]。然而杆件关键系数取值常采用专家打分法，对于结构连续倒塌过程中杆件破坏的传递作用难以预测，使鲁棒性分析结果带有不确定性。

能量法和杆件移除法是经典理论研究方法，然而对于局部失稳易先于整体失稳发生的空间杆系结构(如六角星型穹顶)而言，结构鲁棒性研究成果较为有限，已有研究主要通过理论分析和数值模拟来评价方法可行性或对传统方法进行改进，对结构局部失稳(如跳跃失稳)的破坏模式及其引发的次生倒塌模式也未进行深入探讨，因此有必要进一步研究。

为评价杆系结构鲁棒性并考察不同杆件在结构倒塌破坏过程中的重要性，综合利用应变能敏感度理论和杆件移除法研究了杆系结构鲁棒性的应变能敏感度理论分析方法。通过六角星型穹顶结构室内模型破坏性试验，总结了应变能敏感度随结构破坏模态的变化规律，并与结构鲁棒性应力变化率评价方法相比较，验证了理论分析、数值模拟的可靠性和应变能敏感度法评价结构鲁棒性的可行性。

1 应变能敏感度理论

1.1 杆系结构应变能及敏感度

荷载作用下所产生的结构应变能可作为评价结构鲁棒性的指标。杆系结构中，单元应变能敏感度和节点应变能敏感度分别表示该单元抵抗荷载贡献程度和节点位置变化带来应变能变化程度[13]。

在线弹性条件下，杆系结构应变能的表达式为

(1)

其中：F为作用于杆件上的外力；Δl为杆单元在外力作用下的变形量。

由文献[13]知，单元应变能敏感度为

(2)

其中：U为结构节点位移向量；ΔK为结构总刚矩阵变化量；αi为第i个单元的应变能敏感度。

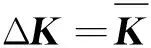
(3)

其中：Ki和ui分别为i单元刚度矩阵和i单元相关的节点位移向量。

某单元被撤除或增加时，结构应变能发生变化，单元应变能敏感度可近似看成结构应变能变量

(4)

其中：C0和C分别为改变单元前后的应变能。

1.2 应变能敏感度分析方法

平面悬臂桁架结构几何尺寸、各杆件及结点编号见图1。竖直集中荷载F施加于结点6，从0开始每5 kN为一荷载步逐级加载至90 kN，各杆件截面面积均为1 000 mm2，弹性模量E均为206 GPa。假设杆件始终处于线弹性范围内，分别考虑只移除杆件10、只移除杆件11及同时移除杆件10和杆件11这3种工况下的平面桁架结构应变能随外荷载增加的结构应变能变化规律。利用数值计算软件Matlab编程计算不同荷载步结构应变能随荷载步变化曲线，如图2所示。同时可获得杆件10和杆件11的杆件应变能敏感度变化曲线，见图3。

图1 悬臂桁架结构Fig.1 Cantilever truss structure

图2 悬臂桁架结构应变能曲线Fig.2 Strain energy curve of cantilever truss structure

由图2可知，随着外荷载增加，结构应变能不断增加，同时应变能变化率不断增大。移除杆件后结构抗弯刚度下降，但在前7个荷载步，由于结构变形较小，移除杆件对结构整体刚度矩阵影响不显著，不同工况间结构应变能数值接近。从第8荷载步开始，移除杆件(即降低结构冗余度)显著地提高了结构应变能数值及应变能变化率，同时移除杆件10和杆件11比仅移除杆件10或杆件11对结构应变能数值及应变能变化率的影响更明显，表明在不改变结构支承条件前提下，增加结构冗余度能降低结构应变能敏感度，提高结构抗倒塌破坏能力。

图3 杆件应变能敏感度曲线Fig.3 Strain energy sensitivity curve of element

由图3可知，分别移除杆件10和杆件11时，随着荷载增大，两根杆件的应变能敏感度均提高，但杆件10的应变能敏感度始终低于杆件11的敏感度，且两根杆件应变能敏感度的差别逐渐加大，表明移除杆件10对结构应变能的影响相对较小。图2曲线上应变能数值差别也验证了这点。

2 六角星型穹顶结构数值模拟

2.1 有限元分析参数

利用通用有限元分析软件ANSYS数值模拟六角星型穹顶结构基本几何尺寸，如图4和图5所示。支座E和支座A距离为2.6 m，结构支座杆件高为0.3 m，中心节点高为0.35 m，钢杆件弹性模量为206 GPa，泊松比为0.3。杆件均采用Q235等截面角钢∠25×3，截面面积为1.43 cm2，材料密度为7.85 g/cm3。数值分析中，杆件采用Link8单元，除支座节点设为固定铰支座外其余节点均为铰接。假设中央节点作用一竖向渐增阶跃集中力，取值从0开始，每隔50 N为一个荷载步，直至结构破坏。结构破坏采用弹塑性破坏判断准则，同时控制结构最大变形和杆件内力。

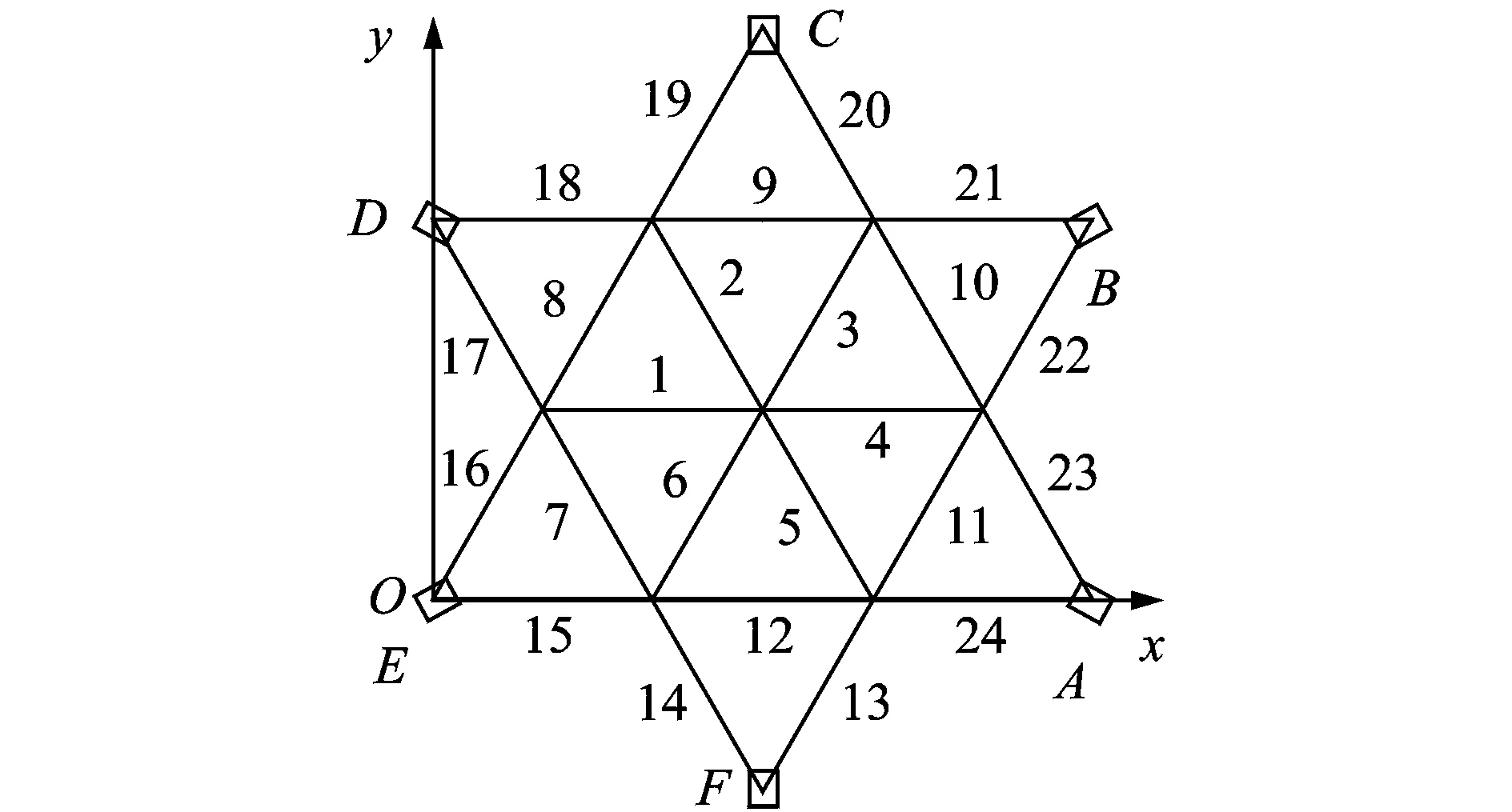
图4 六角星型穹顶结构平面图Fig.4 Plane drawing of hexagonal star-type dome

图5 六角星型穹顶结构侧视图(单位：mm)Fig.5 Vertical drawing of hexagonal star-type dome(unit:mm)

2.2 移除杆件对结构应变能的影响

考虑六角星型穹顶结构的对称性和杆件的受力特征，将杆件分为三类：中心压杆(杆件1～杆件6)、环向拉杆(杆件7～杆件12)和支座压杆(杆件13～杆件24)，从而分别考虑不移除杆件、移除杆件15、移除杆件7和移除杆件1这4种工况，计算4种工况对应的结构应变能变化，如图6所示。

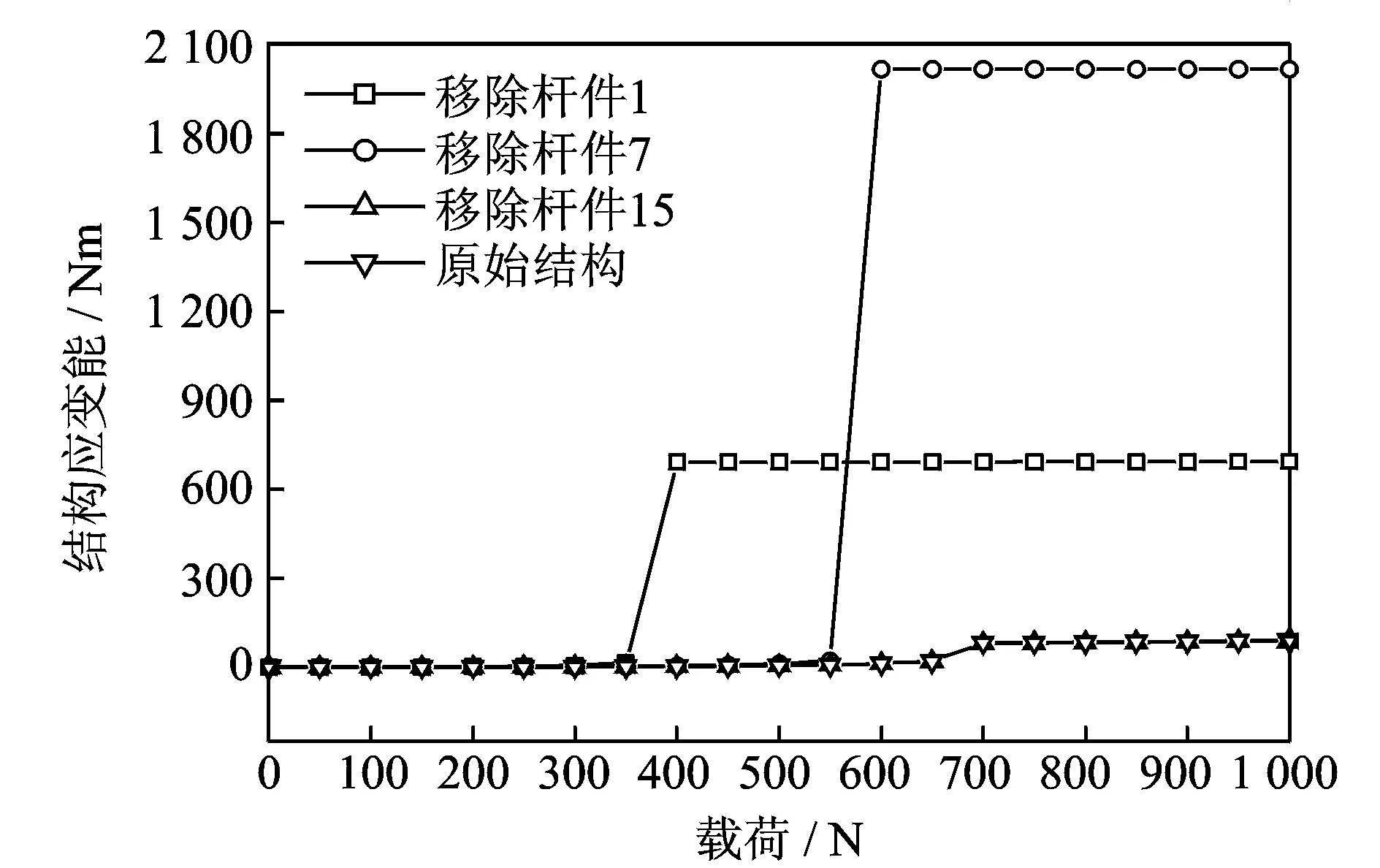
图6 六角星型穹顶结构应变能曲线Fig.6 Strain energy curve of hexagonal star-type dome

由图6知，原始结构和移除杆件15时，结构应变能曲线基本重合，在荷载为700 N之前曲线数值缓慢增加，在650 N时曲线数值突然增大，此后又继续缓慢增加。通过查询结点位移数据可知，荷载为650 N时，中心节点出现了竖向大变形，结构发生跳跃失稳，导致应变能突然增大，随后结构内力重分布，杆件平衡于新位置继续承载。当移除环向杆件7时，结构应变能在550 N时突变，发生跳跃失稳。当移除中心径向杆件1时，结构应变能在350 N时突然变化，发生跳跃失稳。在结构受力至破坏过程中，杆件应变能敏感度变化曲线见图7。

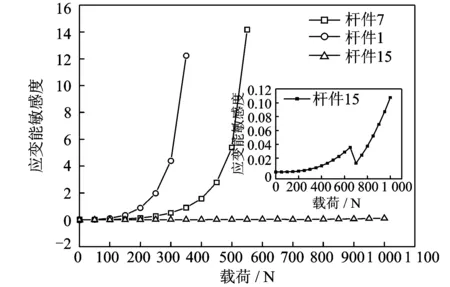
图7 穹顶杆件应变能敏感度曲线Fig.7 Strain energy sensitivity curve of dome element

由图7可知，不同位置的杆件应变能敏感度差异较大。由六角星型穹顶结构的对称性可知，随着中心结点竖向荷载的增加，杆件1～杆件6所形成的压杆群应变能敏感度增加最快，杆件13～杆件24的支座压杆应变能敏感度的数值变化不大。从结构传力路径角度来说，越接近支座的杆件越是结构的关键杆件，因此将杆件15的应变能敏感度变化曲线进一步放大单独分析(见图7)可知，支座杆件15在650 kN时出现了一次显著的应变能敏感度变化，随后应变能敏感度曲线的切线斜率不断加大，结构迅速破坏，反映了移除支座杆件15对结构极限承载能力的影响。受六角星型穹顶结构几何尺寸制约，结构破坏主要表现为中心压杆的跳跃失稳，支座杆件内力变化幅度小于中心压杆，从而导致支座杆件15的应变能敏感度曲线幅值相对较小，同结构破坏规律吻合。同时还表明，对于中心受力的六角星型穹顶结构，制约结构承载能力最强的杆件是外力作用点周围的压杆群，若此处杆件发生破坏将大大削弱结构的稳定承载能力。

为验证上述理论分析结果的可靠性，进行了六角星型穹顶结构模型试验。

3 六角星型穹顶结构模型试验

3.1 模型加工及制作

结构模型试验在中国民航大学机场学院土木工程试验室进行。结构模型尺寸及相关参数与2.1节有限元分析参数相同。6根结构柱采用工字型钢，尺寸规格为100×100×6×8。柱脚焊大底板，利用混凝土重块压稳，柱顶设V型连接板与角钢通过螺栓连接，如图8所示。

将一块规格为1 000 mm×2 400 mm×10 mm的钢板切割为48块规格为100 mm×100 mm的正方形节点连接钢板、6块500 mm×500 mm的正方形柱脚底板和6块200 mm×200 mm的正方形柱顶端板。

图9所示中心节点板为米字型，由6块正方形节点连接钢板焊接而成，并在其中央位置焊一吊钩用来悬挂荷载箱。其余6个节点连接板呈五边形，根据结构杆件空间角度对应设置，并在V型连接板和每块节点板上预留直径为12 mm的螺栓连接孔。螺栓选取直径为10 mm的普通螺栓。杆件选用规格为∠25×3的单角钢，弹性模量为206 GPa。中心压杆(杆件1～杆件6)、环向拉杆(杆件7～杆件12)和支座压杆(杆件13～杆件24)的下料尺寸为867.47，866.03和916.52 mm。所有角钢的预留螺栓孔位置均取在距端部30 mm处，直径为12 mm。

首先，将环向拉杆(杆件7～杆件12)依次组装，摆放在地面上调平临时拧紧；其次，在中央节点板与环向节点板间依次连接中心压杆(杆件1～杆件6)和支座压杆(杆件13～杆件24)；然后，根据6根结构位置，将组装好六角星型穹顶结构主体部分托起分别固定在各个柱顶支座V型板上；最后，根据试验需要调整各个螺栓的拧紧程度。在图10所示不移除杆件工况中，为了和有限元分析结果对比并考察节点连接效果对结构承载力的影响，将杆件和节点板连接处的螺母全部拧松，以模拟铰接连接工况。图11～图13所示对3种工况下杆件和节点板连接处的螺栓全拧紧，以模拟实际工况。

3.2 试验数据采集及分析

在结构杆件上设置应变片，利用DH5908G型动态应变测试系统进行试验数据采集，采样频率为100 Hz。每级加载砝码5 kg模拟阶跃荷载，每级荷载时间间隔约为15 s，加载开始后持续加载直至结构破坏。根据2.2节所述进行了对应4种工况下的结构破坏性试验，相应结构破坏模式的实物照片见图10～图13。

图8 支座节点板图9 中心节点板e

Fig.8 Supporting joint plate Fig.9 Central joint plat

图10 原始结构破坏照片图11 移除杆件1后结构破坏照片

Fig.10 Damage picture oforiginal struchture Fig.11 Damage picture ofremoving element 1

图12 移除杆件7后结构破坏照片图13 移除杆件15后结构破坏照片

Fig.12 Damage picture of removing element 7 Fig.13 Damage picture of removing element 15

对于图10所示纯铰接情况，结构实际破坏情况同有限元分析结果一致，中央节点出现了跳跃失稳。通过有限元分析和实测杆件动态应变，分别计算结构应变能变化曲线，如图14所示，试验结果较好地验证了有限元分析的结论。存在一个明显的区别是两条曲线在400 N时出现了分叉。实测结构应变能曲线斜率变化不大，而理论分析的应变能曲线斜率在400 N时已开始逐渐增大。模型试验实测应变能在650N时出现了跳跃，表明实际的跳跃失稳发生具有突然性，结构并未产生明显的变形，杆件内力仍处在弹性范围内。

图14 结构应变能对比Fig.14 Comparisons of structural strain energy

对于图11～图13所示的移除杆件工况，通过动态应变仪测得的移除相应杆件后杆件5的内力变化情况，见图15。

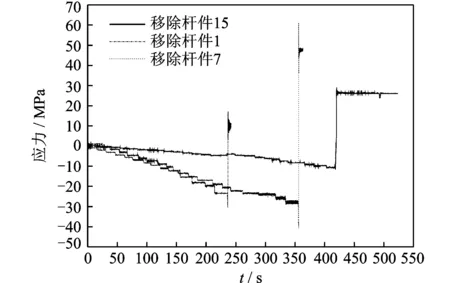
图15 结构杆件动态应力曲线Fig.15 Dynamical stress curve of structural element

与图6和图7所示应变能理论分析结果和应变能敏感度计算结果对比可知，移除杆件后，随着中心节点集中荷载增加，初始阶段结构应变能变化幅度不大。当结构在350，550和650 N时突然发生跳跃失稳时，结构应变能随之发生跳跃并随着结构在新的位置平衡而再次稳定，表明结构虽然发生局部失稳但仍具有一定的承载能力。与图6相对应，结构的应变能敏感度在对应荷载步出现了明显的变化，但不同之处在于移除杆件后结构应变能敏感度在前5个荷载步就出现了上升趋势，表明利用应变能敏感度指标分析破坏模式具有动态性的特点。将上述试验结果与图15所示杆件内力测试结果对比可知，移除中心压杆后结构破坏的临界荷载最小，移除支座压杆后结构破坏的临界破坏荷载最大，同图6和图7所示的结构破坏临界荷载变化规律一致。由于节点连接方式不同，数值分析和模型试验的破坏临界荷载在数值上存在差异。

为进一步分析利用应变能敏感度法评价结构鲁棒性的准确性，将上述试验测试结果利用应力变率法进行比较，见图16，其结果与图6所示结果类似，杆件5的应力变化率随着加载也出现了稳定和跳跃两个阶段。由于应力变率法仅针对单根杆件分析，缺乏对整体杆件变化趋势的预测能力，虽然实现了杆件重要性判别，但在预测局部失稳方面具有一定的局限性，而应变能敏感度法则很好地弥补了这一点。

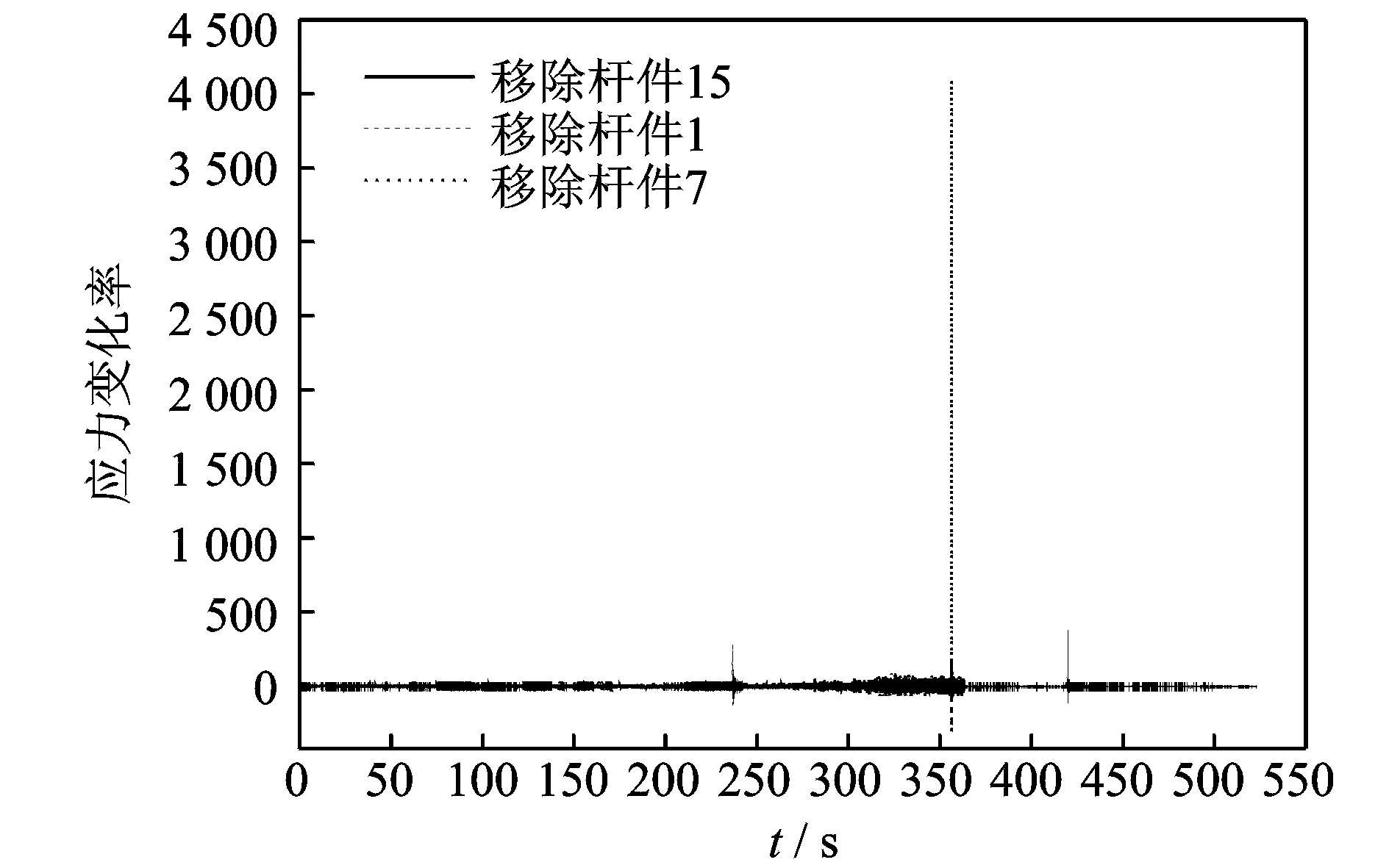
图16 应力变化率法分析结果Fig.16 Analysis result of stress rate method

4 结论

1) 平面悬臂桁架结构应变能计算结果表明，随着变形增大，结构应变能逐渐增加。提高结构冗余度能降低结构的应变能敏感度，从而增强结构鲁棒性。所增加冗余杆件的位置对结构应变能影响也不相同，体现了杆件重要性水平对结构鲁棒性影响的差异性。

2) 六角星型穹顶结构有限元分析和模型试验结果表明，结构应变能在结构破坏前变化较小，在结构破坏时出现明显跳跃，在结构平衡于新位置后再次稳定，表明阶跃跳跃失稳后结构仍具有继续承载能力。

3) 移除杆件位置对结构应变能影响差异性较大，体现了杆件结构重要性的不同。对结构稳定极限承载力影响最大的杆件是中心径向压杆，影响最小的是支座压杆。移除支座杆件所造成的破坏最为严重，在中心压杆群发生跳跃失稳时，由中心压杆群和环向拉杆所形成的闭合结构向着所移除支座杆件一侧发生了整体倾覆。移除环向拉杆7后，中心压杆群整体性工作能力受较大影响，杆件内力变化幅度最大，易引发杆件强度破坏。

4) 结构模型试验得到的杆件内力变化曲线和结构应变能实测曲线验证了应变能敏感度理论分析结果。但从结构破坏模式看，理论上对结构极限承载力影响较低的支座压杆在实际工作中会引起更严重的破坏模式，这是由于结构从局部失稳向整体失稳转化所引起，设计中应予以重视。

5) 同其他结构鲁棒性评价方法相比，应变能敏感度法不但可有效判断杆件重要性，为杆件移除法关键系数的确定提供量化指标，降低鲁棒性分析结果的不确定性，还能识别结构局部失稳模态，具有更好的适用性。

[1] Lucchini A, Greco R, Marano G C, et al. Robust design of tuned mass damper systems for seismic protection of multistory buildings [J]. Journal of Structural Engineering, 2014, 140(8): 1-11.

[2] Lee M C W，Kelly D W，Degenhardt R. A study on the robustness of two stiffened composite fuselage panels[J]. Composite Structures, 2010, 92(2): 223-232．

[3] Baker J W, Schubert M, Faber M H. On the assessment of robustness[J]. Structural Safety, 2008, 30(3): 253-267.

[4] 张成，吴慧，高博青，等. 非概率不确定性结构的鲁棒性分析[J]. 计算力学学报，2013，30(1)：51-56.

Zhang Cheng, Wu Hui, Gao Boqing, et al. Analysis of structural robustness with non-probabilistic uncertainties[J]. Chinese Journal of Computational Mechanics, 2013，30(1)：51-56. (in Chinese)

[5] 喻莹，罗尧治. 基于有限质点法的结构倒塌破坏研究I：基本方法[J]. 建筑结构学报，2011，32(11)：17-26.

Yu Ying, Luo Yaozhi. Structural collapse analysis based on finite particle method I: basic approach[J]. Journal of Building Structures, 2011, 32(11): 17-26. (in Chinese)

[6] 朱红飞，陈务军，董石麟. 杆系结构的弹性冗余度及其特性分析[J]. 上海交通大学学报，2013，43(6)：872-877.

Zhu Hongfei, Chen Wujun, Dong Shilin. Elastic redundancy of pin-jointed bar structures and its characteristics analysis[J]. Journal of Shanghai Jiaotong University, 2013, 43(6): 872-877. (in Chinese)

[7] England J, Agarwal J, Blockley D. The vulnerability of structures to unforeseen events[J]. Computers and Structures, 2008, 86(10): 1042-1051.

[8] 方召欣, 李惠强. 基于能量观点的结构安全性与鲁棒性[J]. 建筑结构学报, 2007, 24(S1): 269-273.

Fang Zhaoxin, Li Huiqiang. Safety and robustness of structures from the viewpoint of energy[J]. Journal of Building Structures, 2007, 24(S1): 269-273. (in Chinese)

[9] 何容，何伟，陈淮，等. 复合边界条件下基于能量法吊索张力实用公式[J]. 振动、测试与诊断，2013, 33(2): 187-191.

He Rong, He Wei, Chen Huai, et al. Practical formula for hanger tension under combined boundary conditions based on energy method[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(2): 187-191. (in Chinese)

[10]崔洋，张雷明. 基于能量流动网络的杆系结构易损性[J]. 工程抗震与加固改造，2012，34(6)：25-32.

Cui Yang, Zhang Leiming. Vulnerability of frame structures based on energy flow network[J]. Earthquake Resistant Engineering and Retrofitting, 2012, 34(6): 25-32. (in Chinese)

[11]詹海雷，肖南. 杆系结构关键单元的整体与局部判定方法[J]. 空间结构, 2014, 20(1): 58-63.

Zhan Hailei, Xiao Nan. The global and local approaches to determine key elements in member structure[J]. Spatial Structure, 2014, 20(1): 58-63. (in Chinese)

[12]郑飞，许金余，颜祥程. 利用单元模态应变能法的地下框架结构损伤诊断[J]. 振动、测试与诊断，2010, 30(6): 642-645.

Zheng Fei, Xu Jinjin, Yan Xiangcheng. Damage diagnosis of underground frame structure using method of element modal strain energy[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(6): 642-645. (in Chinese)

[13]崔昌禹, 姜宝石, 崔国勇. 基于敏感度的杆系结构形态创构方法[J]. 土木工程学报, 2013, 46(4): 1-8.

Cui Changyu, Jiang Baoshi, Cui Guoyong. The sensitivity-based morphogenesis method for framed structures[J]. China Civil Engineering Journal, 2013, 46(4): 1-8. (in Chinese)

[14]苏冠兴，张志强，叶继红. 六角星型穹顶结构易损性分析[J]. 建筑结构学报，2013，34(3): 66-71.

Su Guanxing，Zhang Zhiqiang，Ye Jihong. Vulnerability analysis of hexagonal star-type dome[J]. Chinese Journal of Building Structures, 2013, 34(3): 66-71. (in Chinese)

[15]Lu Jinyu, Luo Yaozhi, Li Na. An incremental algorithm to trace the non-linear equilibrium paths of pin-jointed structures using the singular value decomposition of the equilibrium matrix[J]. Proceedings of the Institution of Mechanical Engineers Part G: Journal of Aerospace Engineering， 2009(223): 881-890.