基于SK和LSSVM的飞机空气制冷机寿命趋势分析*

2016-11-23崔建国滑娇娇董世良齐义文蒋丽英

振动、测试与诊断 2016年3期

关键词：峭度制冷机寿命

崔建国，滑娇娇，董世良，崔霄，齐义文，蒋丽英

(1．沈阳航空航天大学自动化学院沈阳，110136) (2．沈阳飞机设计研究所沈阳，110035)(3．沈阳空气动力研究院沈阳，110134)

基于SK和LSSVM的飞机空气制冷机寿命趋势分析*

崔建国1，滑娇娇1，董世良2，崔霄3，齐义文1，蒋丽英1

(1．沈阳航空航天大学自动化学院沈阳，110136) (2．沈阳飞机设计研究所沈阳，110035)(3．沈阳空气动力研究院沈阳，110134)

针对工程上所获取的飞机空气制冷机信息本身具有的不确定性等特点，提出了谱峭度(spectral kurtosis, 简称SK)和最小二乘支持向量机(least squares support vector machine, 简称LSSVM)相结合的寿命趋势分析方法。首先，将寿命表征参量通过经验模态分解(empirical mode decomposition, 简称EMD)分解为多个固有模态分量(intrinsic mode function, 简称IMF)，分别对多个IMF分量进行傅里叶变换，得到多个频谱，计算每根谱线的谱峭度；其次，通过谱峭度寻找到影响飞机空气制冷机失效的主要IMF分量，对其进行信号重构；最后，提取重构后信号的能量特征，创建最小二乘支持向量机寿命趋势模型，对飞机空气制冷机寿命趋势进行预测。通过对实际监测数据的分析和验证结果表明，该方法可以实现飞机空气制冷机寿命趋势分析效能，具有很好的工程应用价值。

飞机空气制冷机；谱峭度；最小二乘支持向量机；寿命；趋势分析

引言

作为飞机环境控制系统的关键部件之一，飞机空气制冷机的作用是对来自发动机等的高温高压空气进行膨胀做功，将低温低压的空气释放到机舱[1-2]。因此，飞机空气制冷机的正常运转直接影响着飞行员及其电子设备所处的环境温度，一旦在飞机飞行的过程中出现飞机空气制冷机的功能失效状况，将影响某些电子设备的正常工作，甚至造成重大事故。因此，对飞机空气制冷机进行寿命趋势分析显得尤为重要。

近年来，不少学者致力于寿命趋势分析方法的研究。文献[3]提出了基于多变量灰色的分析模型,预测滚珠丝杠的寿命。文献[4]提出了求和自回归滑动平均模型(auto-regressive integrated moving average, 简称ARIMA)，完成了对设备的寿命预测和验证。虽然这两种方法都可以完成设备的寿命趋势预测分析，但当采集到的信息为非线性、非平稳数据时，基于以上两种方法的趋势预测精度会明显下降。文献[5]采用RBF神经网络模型对某装备的故障进行预测，但该模型收敛速度慢，容易陷入局部极小点，对预测误差造成影响。文献[6]采用基于传统支持向量机(support vector machine, 简称SVM)的模型对航空发动机的性能衰退指标进行趋势分析和预测，有效避免了神经网络容易陷入局部极小点的问题。传统SVM模型的训练过程中采用不等式约束，使回归预测中的不确定性增加[7]。针对飞机空气制冷机寿命表征参量中存在的多种不确定因素，如表征空气制冷机寿命的参数通常是非线性、非平稳且伴随随机波动的时间序列，而且空气制冷机的寿命参数测量结果中通常含有噪声等，笔者提出一种基于SK和LSSVM的寿命趋势分析方法。首先，采用适合分析非平稳信号的EMD[8]分解寿命表征参数时间序列，对得到的多个IMF分量分别进行傅里叶变换，得到多个频谱；其次，计算每根谱线上的峭度，从而发现隐藏的非平稳成分[9]，通过谱峭度法找到对飞机空气制冷机失效影响最大的IMF分量，并进行信号合成，经过合成的信号信噪比较高，将有用的信息提取出来，同时使非平稳信号平稳化，减少由于样本点数据不准确对试验结果造成的影响；然后，对合成信号进行特征提取，得到特征向量，减小了样本规模，为后续趋势分析奠定基础；最后，将特征向量作为建模数据，建立LSSVM趋势分析模型，LSSVM模型将传统的SVM模型中的不等式约束变为等式约束，减少了趋势预测的不确定性，从而完成对飞机空气制冷机的寿命趋势预测。通过飞机空气制冷机的振动加速度时间序列趋势分析实例验证了该方法的有效性。

1 相关理论

1.1 谱峭度

谱峭度作为一种统计工具，它可以对信号中的非高斯成分进行度量，并能指出该成分所在的频带[10-11]。谱峭度可解释为理想滤波器组的输出在频率f处得到的峭度值，根据文献[12-13]，Antoni针对能量归一化的四阶谱累积量给出了谱峭度的定义。

(1)

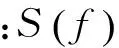
于是，定义谱峭度为

(2)

(3)

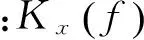
(4)

1.2 最小二乘支持向量机

Vapnik提出的支持向量机成功地解决了非线性函数的回归预测问题，后来Suykens等又提出了最小二乘支持向量机，它以误差平方和损失函数作为训练集的经验损伤，将SVM中的不等式约束变为等式约束，从而减小了回归预测过程中的不确定性，且使算法简练，在求解二次规划问题时节省了时间[14-15]。

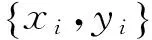
(5)

其中:φ为非线性映射;w∈RN为权向量;b∈R为偏置。

(6)

通过引入拉格朗日乘子αi，定义拉格朗日函数

(7)

根据KKT条件，消去w和ξi，最终得LSSVM模型的预测输出为

(8)

2 寿命趋势分析方法

传统的寿命趋势预测方法直接将采集到的信息序列作为趋势预测模型的输入进行研究，忽略了信息本身的不确定因素，如表征寿命的参数序列通常是非线性、非平稳且伴随随机波动的时间序列，而且这些参数的测量结果中通常含有噪声等。

针对监测信息的不确定性，笔者提出基于SK和LSSVM的寿命趋势方法。采用EMD分解和谱峭度法对监测信号进行滤波，滤除非平稳随机序列中的干扰信息，得到表征寿命的有效信号；对有效信号进行特征提取，基于此特征序列建立LSSVM趋势预测模型，得到趋势预测结果。LSSVM模型将传统的SVM模型中的不等式约束改进为等式约束，减少了趋势预测的不确定性，而且缩短了预测时间。基于SK和LSSVM的寿命趋势分析方法具体步骤如下。

2) 为减小趋势预测模型的样本输入量，对有效信号进行特征提取。首先，对有效信号进行动态分组；其次，计算每组的能量作为特征值；最后，将此特征序列作为趋势预测的基础，建立趋势预测模型，得到趋势预测结果。

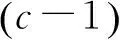
(9)

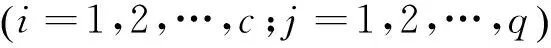
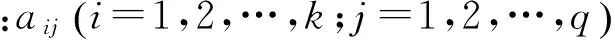
3) 基于得到的特征值序列建立LSSVM趋势分析模型。由于LSSVM更适合小样本、非线性的回归问题，且较传统的SVM模型能节省趋势分析的时间，因此采用LSSVM模型能很好地完成飞机空气制冷机的寿命趋势分析问题。

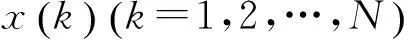
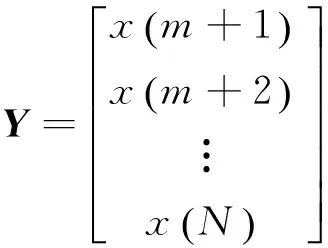
(10)

在得到样本矩阵的基础上，划分LSSVM模型的训练集和测试集。通过训练集样本建立LSSVM模型，并对模型进行训练；通过测试集对模型进行测试，得到能量值序列的趋势预测值，从而完成飞机空气制冷机的寿命趋势分析。

基于SK和LSSVM的寿命趋势分析方法如图1所示。

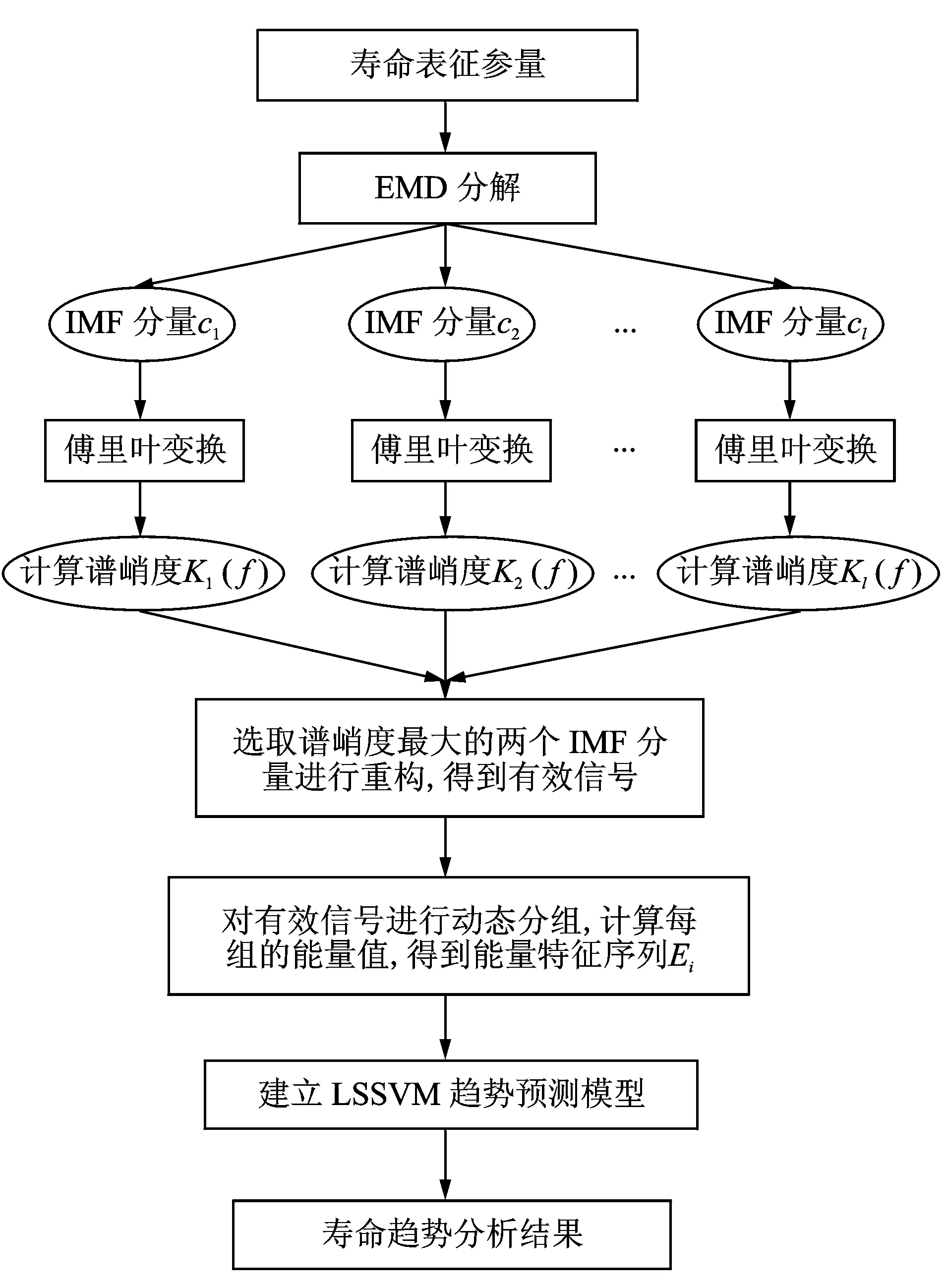
图1 基于SK和LSSVM的寿命趋势分析方法Fig.1 Life trend analysis method based on SK and LSSVM

3 飞机空气制冷机寿命趋势分析试验

3.1 飞机空气制冷机寿命试验

针对某型飞机空气制冷机，依托寿命趋势分析试验台进行加速寿命试验，采集到飞机空气制冷机由正常工作到功能失效的大量信息。本试验采集到的参数有进口温度、出口温度、进口压力、出口压力、进口流量、出口流量、转速和振动加速度等。由于飞机空气制冷机的寿命试验为机械振动试验，因此，采用最能表征飞机空气制冷机寿命的参量——振动加速度作为研究对象，完成对飞机空气制冷机的寿命趋势分析。

飞机空气制冷机寿命趋势分析试验的采样频率f=0.1 Hz ，试验采集到的飞机空气制冷机振动加速度原始数据如图2所示。由图可以看出，飞机空气制冷机从正常运行到功能失效共采集到4 200个采样点，实际运行时间为11.7 h，且在第3 975个采样点(运行11 h)时空气制冷机失效。

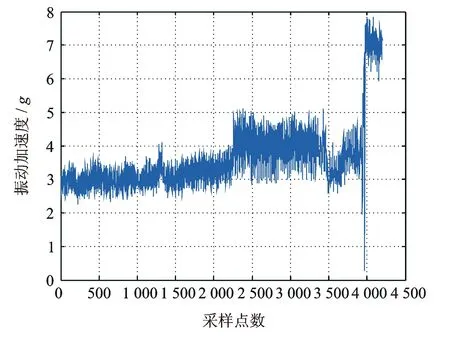
图2 振动加速度原始数据Fig.2 Original data of vibration acceleration

3.2 基于EMD和谱峭度的有效信号的获取

EMD分解可以将振动加速度时间序列中真实存在的不同尺度或趋势项逐级分解出来，产生一系列具有相同特征尺度的时间序列，分解后的序列与振动加速度原始数据序列相比，具有更强的规律性。

经EMD分解后，共得到了10个IMF分量和1个余量。由于篇幅限制，此处仅给出其前6个IMF分量，如图3所示。

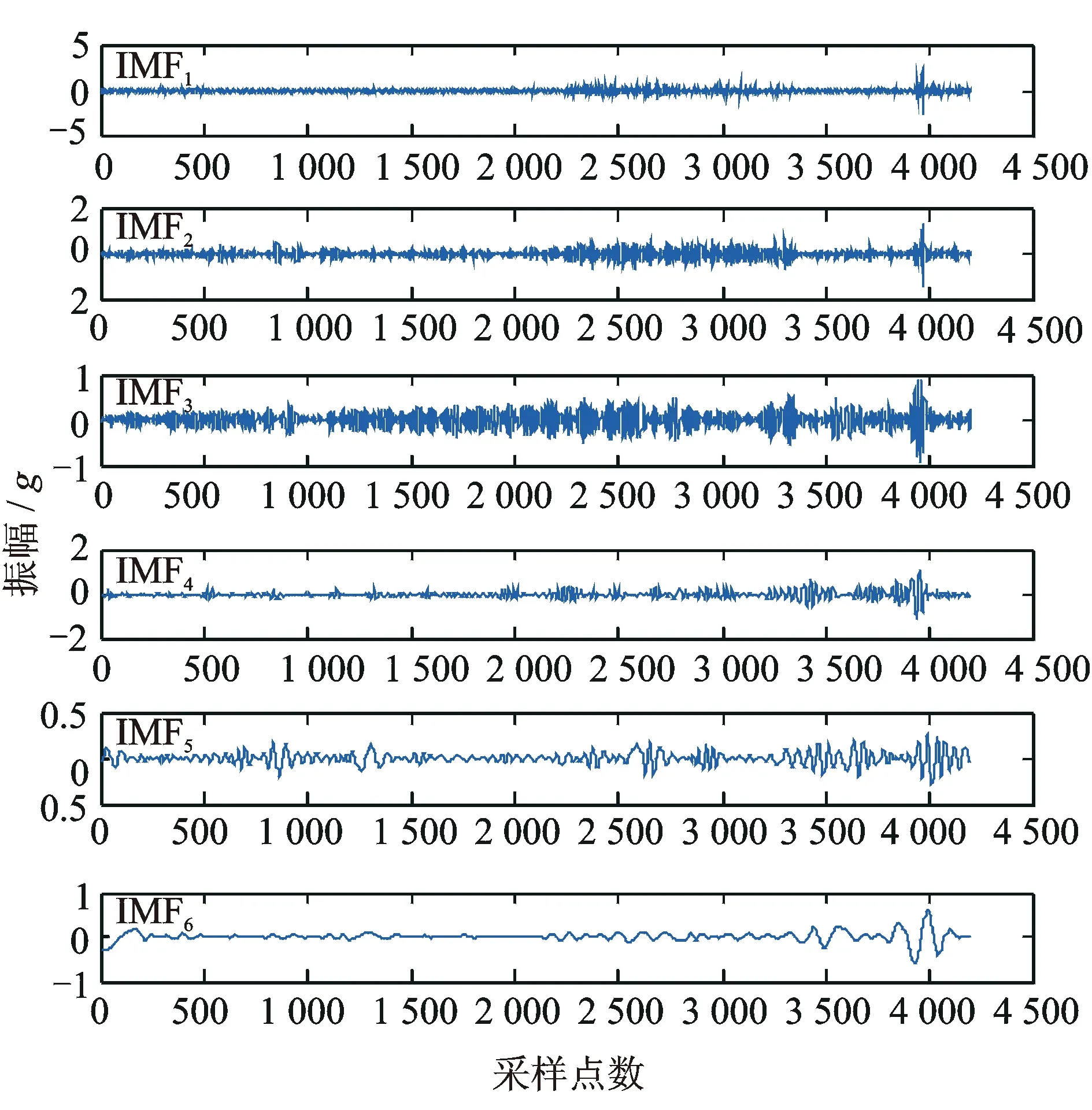
图3 EMD分解得到的部分IMF分量Fig.3 Some IMFs decomposed by EMD

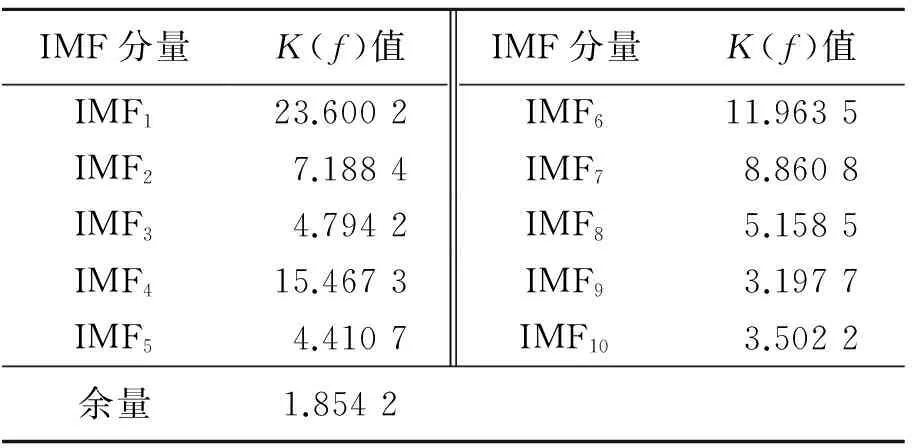
对得到的10个IMF分量分别进行傅里叶变换，得到10条谱线。根据式(3)分别对每条谱线求谱峭度。IMF分量对应的谱峭度值如表1所示。

表1 IMF分量对应的谱峭度值

Tab．1 Spectral kurtosis values corresponding to the IMF components

IMF分量K(f)值IMF分量K(f)值IMF123.6002IMF611.9635IMF27.1884IMF78.8608IMF34.7942IMF85.1585IMF415.4673IMF93.1977IMF54.4107IMF103.5022余量1.8542

由表1可知，IMF1和IMF4的谱峭度值最大。将IMF1分量和IMF4分量进行合成，即可得到表征飞机空气制冷机寿命的有效信号，如图4所示。

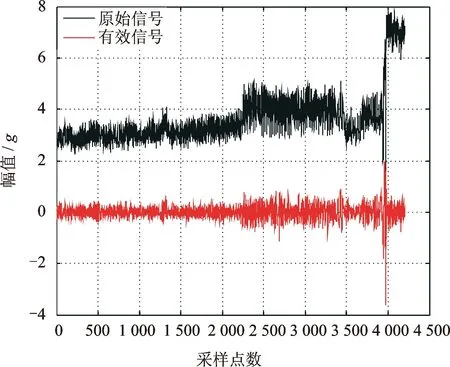
图4 基于EMD和谱峭度提取的有效信号Fig.4 The valid signal extracted by EMD and SK

由图4可明显看出，基于EMD和谱峭度法提取得到的飞机空气制冷机有效信号，相比于振动加速度原始序列变得更加平稳。在不同健康状态，有效信号幅值也不同。如在空气制冷机失效瞬间，有效信号幅值大幅度增加。因此，可采用提取有效信号能量的方法来为后续趋势预测做准备。

3.3 有效信号的能量特征提取

由EMD分解和谱峭度法提取的有效信号，在不同时间段具有不同的能量值。因此，在对有效信号提取能量特征之前，先对有效信息进行动态分组。

取q=900，p=30，则c=111。将N=4 200个有效信号样本值动态分组：每组900个样本值，1～900个样本值序列为第1组，以30为步长依次向后移动，则第2组为第31～930个样本值序列，以此类推，共分为111组，第111组为第3 301～4 200个样本值序列。由于在第3 975个采样点时飞机空气制冷机失效，将此对应到动态分组中，从第104组开始包含失效点，第1～103组为飞机空气制冷机的正常运行数据。由于采样频率为f=0.1 Hz，则采集30个采样点对应的时间为5 min，即动态分组中依次由5 min的新信息更换5 min的旧信息。

根据式(9)计算每组样本值序列的能量值E，得到的能量值序列如图5所示。

图5 有效信号的能量特征Fig.5 Energy characteristic of effective signal

由图5可知，飞机空气制冷机失效后，能量值呈单调递增趋势，且在整个试验过程中，空气制冷机的能量呈整体上升趋势。因此，可将此特征序列作为研究对象，对飞机空气制冷机进行寿命趋势预测研究。

3.4 寿命趋势分析方法试验验证

将能量特征序列作为建模数据，建立LSSVM

趋势预测模型。笔者以常用的RBF核函数作为LSSVM模型预测的核函数。RBF核函数如下

(11)

其中：σ为核函数宽度，本研究取σ=4.67。

由式(10)对能量特征序列进行相空间重构。选取LSSVM模型的正则化参数为100，嵌入维数为5。选取相空间重构后的前40组数据作为建模数据，对模型进行训练，其余数据作为测试数据，对飞机空气制冷机进行寿命趋势分析。

传统SVM在超平面参数选择时采用不等式为约束条件，在求解二次规划问题时导致矩阵规模受训练样本数目的影响很大。下面采用传统SVM对相空间重构后的能量值序列进行预测，将结果与LSSVM的预测结果进行对比。其中，SVM的参数选取(正则化参数和核函数宽度)与LSSVM的一致。

基于LSSVM模型及SVM模型得到飞机空气制冷机的寿命趋势预测结果直观图如图6所示，两种模型的预测结果及误差见表2。

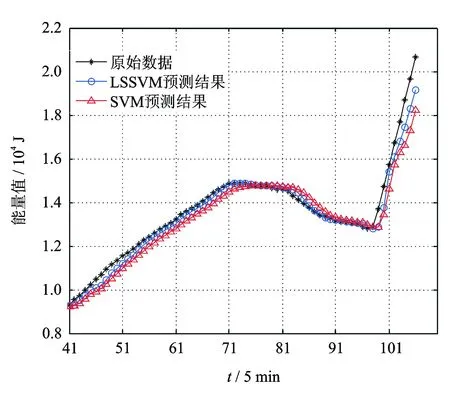
图6 基于LSSVM的飞机空气制冷机寿命趋势预测Fig.6 Aircraft air refrigerator′s life trend predict based on LSSVM model

表2 两种预测方法对能量值的预测结果

基于LSSVM的预测模型建立在结构风险最小化的基础上，由图6和表2可得，基于LSSVM的预测模型具有较强的泛化能力，且预测精度比传统SVM的精度高。因此，可采用基于LSSVM的预测模型完成对飞机空气制冷机的寿命趋势预测。

4 结束语

针对飞机空气制冷机监测信息本身具有的不确定性等特点，提出了一种基于SK和LSSVM相结合的寿命趋势分析方法。该方法通过计算EMD分解空气制冷机振动加速度得到的IMF分量的谱峭度，找到影响飞机空气制冷机失效的两个主要IMF分量，通过对该两个IMF分量进行重构，可得到表征飞机空气制冷机寿命的有效信号。提取有效信号的能量作为空气制冷机的寿命特征，并由所建立的LSSVM模型对其进行寿命趋势分析。研究表明，基于SK和LSSVM的寿命趋势分析方法可以很好地实现飞机空气制冷机寿命趋势的准确预测，且预测精度比传统的SVM更高，具有很好的工程应用前景。

[1] 林韶宁,夏葵,李军,等. 空气制冷机在飞机空调系统中的应用[J]. 流体机械,2005,32(10):46-49.

Lin Shaoning,Xia Kui,Li Jun,et al. Application of air refrigerator in aircraft air condition system[J]. Fluid Machinery, 2005,32(10):46-49. (in Chinese)

[2] 任金禄. 空气制冷机[J]. 制冷与空调, 2008,8(6):15-21.

Ren Jinlu. Air refrigerator[J]. Refrigeration and Air-conditioning, 2008,8(6):15-21. (in Chinese)

[3] 赵敏,高宏力,许明恒,等. 多变量灰色模型在滚珠丝杠剩余寿命预测中的应用[J]. 计算机集成制造系统,2011,17(4):846-851.

Zhao Min,Gao Hongli,Xu Mingheng,et al. Application of multi-variable grey model for ball screw remaining life prediction[J]. Computer Integrated Manufacturing Systems,2011,17(4):846-851. (in Chinese)

[4] 李晓白,崔秀伶,郎荣玲. 航空发动机性能参数预测方法[J]. 北京航空航天大学学报,2008,34(3):253-256.

Li Xiaobai,Cui Xiuling,Lang Rongling. Forecasting method for aeroengine performance parameters[J]. Journal of Beijing University of Aeronautics and Astronautics,2008,34(3):253-256. (in Chinese)

[5] 黄波,丁浩,张孝芳,等. 基于RBF神经网络的某复杂装备故障预测方法[J]. 计算机仿真,2014,31(1):14-17.

Huang Bo,Ding Hao,Zhang Xiaofang,et al. Prediction method of complex equipment based on RBF neural network[J]. Computer Simulation,2014,31(1):14-17. (in Chinese)

[6] 谭巍,徐健,于向财. 基于支持向量机的航空发动机性能衰退指标预测[J]. 航空发动机, 2014,40(4):51-55.

Tan Wei,Xu Jian,Yu Xiangcai. Prediction of aeroengine performance deterioration index based on support vector machine[J]. Aeroengine,2014,40(4):51-55. (in Chinese)

[7] 张弦,王宏力. 基于支持向量经验模态分解的故障率时间序列预测[J]. 航空学报, 2011,32(3):480-487.

Zhang Xian,Wang Hongli. Failure rate time series prediction based on support vector empirical mode decomposition[J]. Acta Aeronautica et Astronautica Sinica, 2011,32(3):480-487. (in Chinese)

[8] Napolitano G,Serinaldi F,See L. Impact of EMD decomposition and random initialisation of weights in ANN hindcasting of daily stream flow series:an empirical examination[J]. Journal of Hydrology,2011,406(3):199-214.

[9] 蔡改改,刘海洋,黄伟国,等. 自适应谱峭度滤波方法及其振动信号检测应用[J]. 振动、测试与诊断, 2014,34(2):212-217.

Cai Gaigai,Liu Haiyang,Huang Weiguo,et al. Adaptive kurtosis spectrum filtering method and its application in vibration signal detection[J]. Journal of Vibration,Measurement & Diagnosis, 2014,34(2):212-217. (in Chinese)

[10]Antoni J. The spectral kurtosis of nonstationary signals:formalization,some properties,and application[C]∥12th European Signal Processing Conference. Vienna,Austria:[s.n.],2004.

[11]蔡艳平，李艾华，石林锁，等. 基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J]. 振动与冲击，2011，30(2)：167-172.

Cai Yanping,Li Aihua,Shi Linsuo,et al. Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J]. Journal of Vibration and Shock,2011，30(2)：167-172. (in Chinese)

[12]刘亭伟. 基于谱峭度的齿轮箱故障特征提取[D]. 昆明：昆明理工大学，2011.

[13]Antoni J,Randall R B. The spectral kurtosis a useful tool for characterisingnonstationarysignals[J]. Mechanical Systems and Signal Processing,2006,20(2):282-307.

[14]Suykens J A K,Brabanter J D,Lukas L. Weighted least squares support vector machines:robustness and sparse approximation[J]. Neurocomputing,2002,48(10):85-105.

[15]梁昔明,阎纲,李山春,等. 基于最小二乘支持向量机和混沌优化的非线性预测控制[J]. 信息与控制,2010,39(2):129-135.

Liang Ximing,Yan Gang,Li Shanchun,et al. Nonlinear predictive control based on least squares support vector machines and chaos optimization[J]. Information and Control, 2010,39(2):129-135. (in Chinese)

[16]Samui P,Kothari D P. Utilization of a least square support vector machine (LSSVM) for slope stability analysis[J]. ScientiaIranica,2011,18(1):53-58.

[17]Akpinar E K,Akpinar S. An assessment on seasonal analysis of wind energy characteristics and wind turbine characteristics[J]. Energy Conversion and Management,2005,46(11):1848-1867.

[18]邹敏,周建中,刘忠,等. 基于支持向量机的水电机组状态趋势预测研究[J]. 水力发电, 2007,33(2):63-65.

Zou Min,Zhou Jianzhong,Liu Zhong,et al. Research on condition trend prediction of hydro-turbine generating unit based on support vector machines[J]. Water Power,2007,33(2):63-65. (in Chinese)

[19]孙鑫晖,张令弥,王彤. 基于奇异值分解的频响函数降噪方法[J]. 振动、测试与诊断,2009,29(9):325-328.

Sun Xinhui,Zhang Lingmi,Wang Tong. Noise reduction of frequency response function using singular value decomposition[J]. Journal of Vibration,Measurement & Diagnosis,2009,29(9):325-328. (in Chinese)

[20]Xia D,Song S,Wang J,et al. Determination of corrosion types from electrochemical noise by phase space reconstruction theory[J]. Electrochemistry Communications,2012,15(1):88-92.