基于半监督谱核聚类的转子系统故障诊断*

2016-11-23李城梁

振动、测试与诊断 2016年3期

关键词：扇叶投影约束

李城梁，马芸，张锐，魏伟

(西安导航技术研究所西安，710000)

基于半监督谱核聚类的转子系统故障诊断*

李城梁，马芸，张锐，魏伟

(西安导航技术研究所西安，710000)

针对机械系统故障诊断中对先验知识利用不足和在高维特征空间中诊断难的问题，提出了一种基于成对约束和通过约束准则构造核函数的半监督谱核聚类方法。首先，在训练集中利用先验知识建立约束点对，即属于同一聚类的must-link点对和不属于同一聚类的cannot-link点对；其次，通过样本连接图的结构信息和约束点对信息设计核函数，计算出投影矩阵；最后，在投影空间中使用k-means算法聚类。测试集的每个样本点找到在对应训练集中k个近邻样本的投影值，计算局部投影矩阵，从而可以在线计算出每个新来样本的投影值。实验表明，该算法较相关比对算法聚类准确率更高，可以满足转子系统故障诊断的实际需要。

成对约束；半监督聚类；故障诊断；转子系统

引言

随着人工智能和计算机技术的飞速发展，基于智能方法的机械故障诊断技术成为研究热点，诸多智能方法已经被应用到机械故障诊断领域，例如自组织特征映射(SOM)[1]、支持向量机[2]以及聚类算法[3-4]等。但这些方法往往存在对先验知识利用不足以及在高维特征空间中诊断性能下降的缺陷。

为了克服这些问题，已有学者开展了相关的研究。Jiang等[5]利用训练集全部样本数据的标签信息去引导Laplacian映射算法进行样本数据的降维，提出了监督型流形学习的机械故障诊断方法。张育林等[6]采用自适应局部线性嵌入对原始样本数据进行非线性降维，应用递归调用规范切对低维空间数据进行聚类，提出了一种自适应局部线性嵌入与谱聚类融合的故障诊断方法。基于半监督的聚类方法在故障诊断领域中有相关应用，并取得优越的性能。毕锦烟等[7]将基于半监督学习的模糊核聚类方法用于齿轮箱离群故障的检测。徐超等[8]提出一种将改进半监督模糊C-均值聚类算法应用于发动机磨损故障诊断。在无监督学习中通过图Laplacian的特征值和特征向量建立起来的核函数矩阵称之为谱核学习[9]。近年来，谱核学习方法在图像识别领域[10]和故障诊断领域[11]得到应用。

笔者提出了一种基于成对约束和通过约束准则构造核函数的半监督谱核聚类方法(semi-supervised spectrum kernel clustering，简称S3KC)。在训练集中利用先验知识建立约束点对，通过样本连接图的结构信息和约束点对信息设计核函数，计算出投影矩阵，最后在投影空间中使用k-means算法聚类。测试集的每个样本点找到在对应训练集中k个近邻样本的投影值，计算局部投影矩阵，从而可以在线计算出每个新来样本的投影值。用美国凯斯西储大学电气工程实验室的滚动轴承实验数据对算法与相关比对算法进行了聚类精度比较实验，结果表明该方法的优越性，在实测数据上进行的实验也证明该方法可以满足转子系统故障诊断的实际需要。

1 谱核学习

(1)

(2)

传统的谱聚类方法使用最小的前k个(聚类数量)特征值对应的特征向量去揭示数据的聚类结构，这证明了谱聚类的主要特性：局部近邻信息被最优的保存，近距离的数据点应该被分到同一聚类。

(3)

(4)

笔者将特征相似性和成对约束信息结合提出一种新的谱核方法以提高聚类精度。

2 带约束的半监督谱核学习

(5)

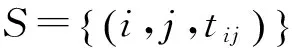
(6)

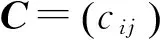
(7)

问题转化为优化式(7)

(8)

(9)

去除c,优化问题式(8)最终转化为标准的二次规划问题

(10)

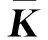
1) 构建稀疏对称的相似矩阵W=(wij)；

测试阶段具体步骤包括：

4) 对测试集应用k-means聚类算法在投影空间进行聚类。

3 半监督谱核聚类算法在转子系统中的应用

由图1可知，应用本研究方法对转子系统进行故障诊断。首先,从传感器采集转子系统振动信号(振动加速度或位移信号)，将历史数据作为训练数据加窗分段并提取特征，构成训练样本集合；然后，将训练集和选取的约束点对输入该聚类算法中，可以得出训练样本的投影结果和聚类结果。在测试阶段，新进入样本找出训练集中k近邻点集，计算出局部映射矩阵和新样本的映射值，最后用k均值聚类算法进行聚类得出最终的故障诊断结果。

图1 基于半监督谱核聚类算法的转子系统故障诊断模型Fig.1 The flow chart of fault diagnosis of rotor system base on proposed method

4 实验验证

4.1 性能分析

应用对象选择来自美国凯斯西储大学电气工程实验室的滚动轴承实验数据[12]，滚动轴承型号为6203-2RS JEM SKF，采样频率为12 kHz。选择内环、外环、滚动体的损伤直径为0.533 4 mm的故障状态以及正常状态下的振动数据，每组数据通过建立样本的特征空间。首先通过滑动时间窗来计算得到每一样本的特征向量，本实验中，滑动时间窗中包含2 048个采样点，滑动步长为半个窗长。通过加窗后每组信号得到的样本数为64，4组信号共计样本数为256。笔者用15种无量纲特征来构建特征空间，特征包括均值、中位数、方差、偏斜度、最小值、求和、标准误差、标准差、峭度、值域、最大值、奇异值熵、EMD能量熵、频域最大值和均值的比值以及频域的均方误差。笔者用方差取1的高斯核函数来计算特征空间中的样本点之间的权值距离。图2分别为截取1个滑动窗内4种正常状态下的信号图，在投影空间中将原始空间降到4维。

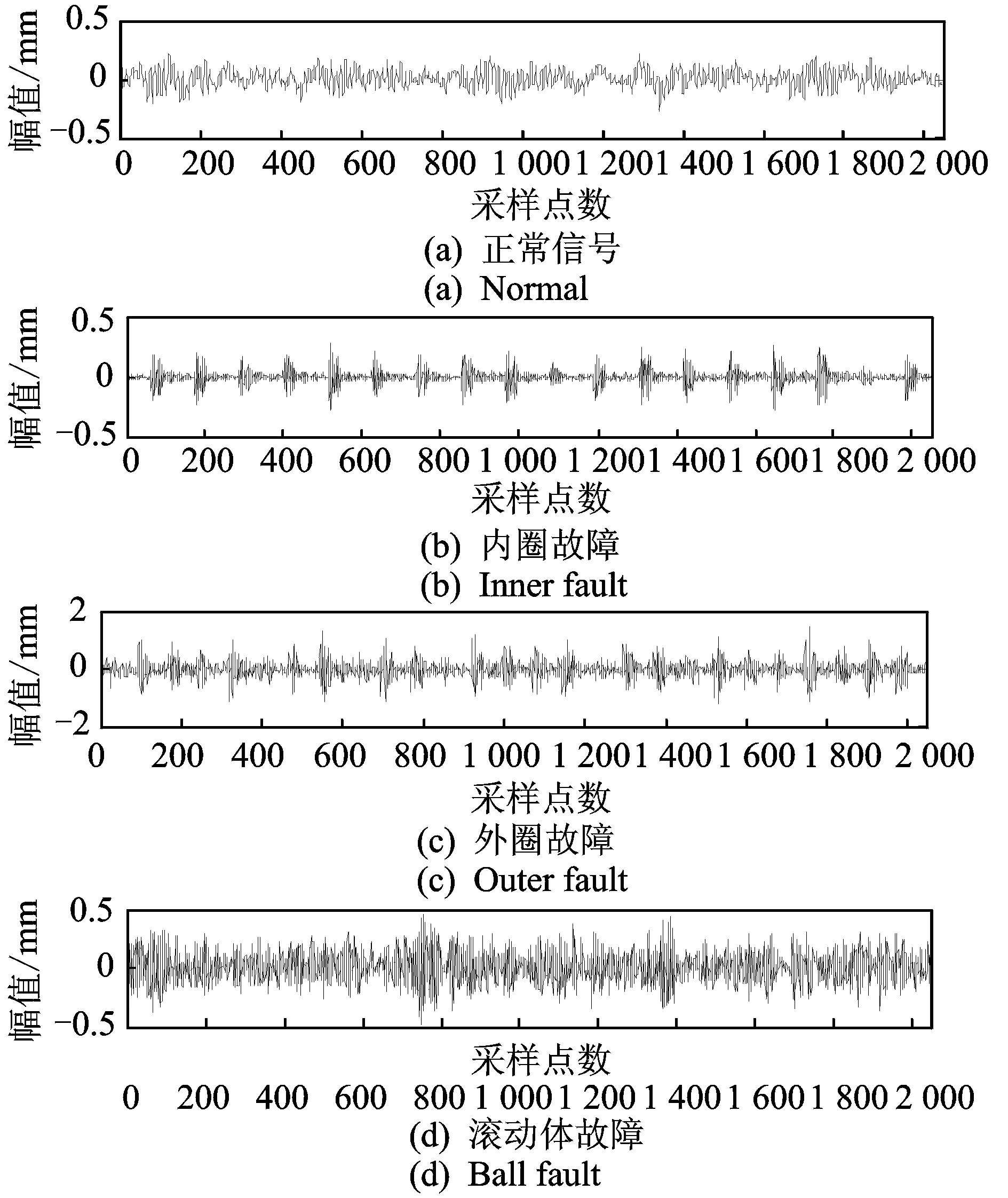
图2 截取1个Outer fault滑动窗内的信号图Fig.2 The segmention of signal in one slide window

投影结果和聚类精度分别用样本距离矩阵灰度图和聚类误差率式(11)来表示

(11)

为了可以将投影得到的无量纲的4维数据结果可视化，笔者用3幅三维可视化图对投影的结果进行显示，图3所示为约束点数为16情况下的投影结果。图3(a)为在第1，2，3主分量上的投影图，图3(b)为在第1，2，4主分量上的投影图，图3(c)为在第2，3，4主分量上的投影图。从投影结果可以得知，不同类之间距离较远，同类之间距离较近。将本方法和其他典型的聚类方法如半监督核k均值算法(SSKK)、谱学习(SL)、正则化图割算法(Ncuts)，对比在设置集合M和C约束点对个数变化的情况下的聚类精度。图4(a)

为原始特征空间样本距离矩阵灰度图，其中像素点颜色越深，表示对应的样本点对距离越近。可以看出，在原始的特征空间中，内圈、外圈、滚动体这3种状态样本不同类之间距离近，产生混叠。图4(b)是应用本研究方法，集合M和C中约束点对数分别在20时的投影空间样本距离矩阵灰度图，可以看出4种状态样本不同类之间距离远，同类之间距离近。

图3 约束点对数为16情况下数据的投影结果Fig.3 The projection in the case which the number of constraint pairs is 16

图4 距离矩阵灰度图Fig.4 The grayscale of the distance matrix

由图5可以得出，笔者提出的方法的聚类误差率最低。谱聚类方法和本研究方法优于半监督核k均值算法，表明约束点对的应用在这两种算法上是有效的，正则化图割算法性能较半监督核k均值算法差。随着约束点对数的增加，SSKK, SL和S3KC聚类误差率都在下降，但S3KC下降最快，并在约束点对数为总样本点数的12.5%(16对)时聚类误差为0，再增加约束点对数时聚类误差保持0不变，充分说明该方法在约束对的信息传播性能上较前3种方法具有优势。

图5 不同数量约束点对时的聚类误差率Fig.5 Clustering error in different number of constraint pairs

实验中用到的计算机的微处理器配置为2.14 GHz Inter(R) Core(TM)2 Duo CPU, 2 GB RAM，算法S3KC， SSKK， SL 和Ncuts的运算时间分别为15,18,17和21 s。由于本算法是用二次规划进行的优化求解，在优化过程中仅用了0.2 s，所以该算法在计算效率上同样具有优势。

4.2 两类突发性故障诊断实验

通过转子实验台驱动特殊加工过的扇叶来模拟航空发动机扇叶突发性断裂故障和扇叶异物吸附实验。实验之前，通过调整扇叶中的1片叶片的固定松紧程度，使其能在一定的转速下通过离心力作用将其甩出，从而模拟航空发动机扇叶突发性断裂的故障。在扇叶转动过程中，用带有磁性的金属块投向叶片，金属片通过磁力吸附在转动的叶片上可以模拟航空发动机扇叶突发性吸附故障。笔者所用的实验数据是该实验台在400，600r/min两种转速下采集到的突发性断裂数据和突发性吸附数据，共6组数据。用电涡流传感器采集滚轴垂直方向上的振动位移信号，采样频率设定为512 Hz，采样时间为20 s。图6为两种转速下扇叶吸入故障和扇叶断裂故障信号图。为了能够说明本研究方法故障诊断的有效性，所用实验数据只是截取故障发生后的信号。原始样本特征空间同样由上组实验的15维特征构成。每一种转速下每一类分别有47个训练样本和47个测试样本，每一组训练集中集合M和C中约束点对数分别为10。

图6 两种转速下扇叶吸入故障和扇叶断裂故障信号图Fig.6 The signal of fan inhalation and fan crack in two speed

如图7(a)，(b)分别表示两种转速下训练集样本在原始特征空间中的距离矩阵灰度图，可以看出，在原始特征空间中扇叶断裂故障和扇叶吸附故障样本产生严重混叠。

图7 不同转速下两类故障训练集样本在原始特征空间中的距离矩阵灰度图Fig.7 The grayscale of the distance matrix of two class training data set in different speed

从表1的实验结果可以看出，扇叶断裂故障样本和扇叶吸附故障样本在原始特征空间中产生混叠的情况下，诊断正确率均可以达到90%以上，表明该方法在故障诊断的应用中是有效的。

表1 本研究方法得出的突发故障诊断结果

Tab.1 Fault diagnosis results obtained in proposed method

测试集样本总数诊断出断裂故障数诊断出吸附故障数诊断准确率400r/min下的两类故障9438560.904600r/min下的两类故障9443510.957

5 结束语

在转子系统故障诊断的实际应用中容易得到成对约束的先验知识，充分有效地利用这些先验知识可以提高聚类的性能。笔者将谱核学习方法引入到转子系统故障诊断中，提出了一种基于成对约束和通过约束准则构造核函数的半监督谱核聚类方法。在训练集中利用先验知识建立约束点对，通过样本连接图的结构信息和约束点对信息设计核函数，计算出投影矩阵，然后在投影空间中进行聚类。测试集的每个样本点找到在对应训练集中k个近邻样本的投影值，计算局部投影矩阵，从而可以在线计算出每个新来样本的投影值。用美国凯斯西储大学电气工程实验室的滚动轴承试验数据对算法与相关比对算法进行了聚类精度比较实验，结果表明该方法的优越性。在实测数据上进行的实验也证明该方法可以满足转子系统故障诊断的实际需要。

[1] Kohonen T，Self-organization and associative memory[M]. Berlin: Springer，1988:95-127.

[2] Yuan Shengfa，Chu Fulei. Fault diagnostics based on particle swarm optimisation and support vector machines[J]. Mechanical Systems and Signal Processing， 2007， 21(4)：1787-1798.

[3] 崔宝珍，王泽兵，潘宏侠. 小波分析-模糊聚类法用于滚动轴承故障诊断[J]. 振动、测试与诊断， 2008， 28(2): 151-154.

Cui Baozhen, Wang Zebing, Pan Hongxia. Application of wavelet analysis-cluster fuzzy to fault diagnosis of roller bearings[J]. Journal of Vibration, Measurement & Diagnosis, 2008， 28(2): 151-154.(in Chinese)

[4] 周云龙, 王锁斌, 赵鹏. 基于改进k-均值聚类算法的风机振动分析[J]. 振动、测试与诊断，2012，32(3):437-440.

Zhou Yunlong, Wang Suobin, Zhao Peng. Fan fault analysis based on time domain features and improved k-means clustering algorithm[J]. Journal of Vibration, Measurement & Diagnosis, 2012，32(3):437-440.(in Chinese)

[5] Jiang Quansheng， Jia Minping， Hu Jianzhong， et al. Machinery fault diagnosis using supervised manifold learning[J]. Mechanical Systems and Signal Processing，2009,23: 2301-2311.

[6] 张育林，庄健. 一种自适应局部线性嵌入与谱聚类融合的故障诊断方法[J]. 西安交通大学学报， 2010， 44(1): 77-82.

Zhang Yulin, Zhuang Jian. Fusion of adaptive local linear embedding and spectral clustering algorithm with

application to fault diagnosis[J]. Journal of Xi′an Jiaotong University, 2010， 44(1): 77-82.(in Chinese).

[7] 毕锦烟，李巍华. 基于半监督模糊核聚类的齿轮箱离群检测方法[J]. 机械工程学报，2009，45(10): 48-52.

Bi Jinyan, Li Weihua. Semi-supervised kernel-based fuzzy clustering for gear outlier detection[J]. Journal of Mechanical Engineering, 2009，45(10): 48-52.(in Chinese)

[8] 徐超，张培林，任国全，等. 基于改进半监督模糊C-均值聚类的发动机磨损故障诊断[J]. 机械工程学报， 2011，47(17): 55-59.

Xu Chao, Zhang Peilin, Ren Guoquan, et al. Engine wear fault diagnosis based on improved semi-supervised Fuzzy C-means clustering[J]. Journal of Mechanical Enginineering, 2011，47(17): 55-59.(in Chinese)

[9] Zhang Tong, Ando R. Analysis of spectral kernel design based semi-supervised learning. [C]∥ Neural Information Processing Conference.[S.l.]：Springer，2006.

[10]Li Zhenguo，Liu Jianzhuang，Tang Xiaoou. Constrained clustering via spectral regularization. [C]∥IEEE Conference on Computer Vision and Pattern Recognition.[S.l.]:IEEE, 2009.

[11]李志农，王心怡，张新广, 等. 基于全矢谱核函数主元分析的旋转机械故障诊断方法研究[J]. 振动与冲击， 2008，27(7): 55-58.

Li Zhongnong, Wang Xinyi, Zhang Xinguang, et al. Fault diagnosis method for rotating machinery based on full vector spectrum and kernel principle component analysis[J]. Journal of Vibration and Shock, 2008，27(7): 55-58.(in Chinese)

[12]The Case Western Reserve University Bearing Data Center. Bearing data center fault test data[EB/OL]. [2011-01-01]. http：∥www.eecs.cwru.edu/laboratory/ bearing/.