轮胎动平衡试验机系统偏心的动态补偿*

杨静芳， 冯显英， 张 鹏, 王家寅

(1.齐鲁工业大学机械与汽车工程学院 济南,250353) (2.山东大学机械工程学院 济南，250061)



轮胎动平衡试验机系统偏心的动态补偿*

杨静芳1， 冯显英2， 张 鹏2, 王家寅2

(1.齐鲁工业大学机械与汽车工程学院 济南,250353) (2.山东大学机械工程学院 济南，250061)

较大的系统偏心量是影响轮胎动平衡试验机测试精度、重复性和稳定性的一个重要因素，当前的偏心补偿操作求出系统偏心量后仅用于后续解算，而鲜有将其消除或减小的结构或措施。针对此问题，基于原有的机械结构和解算原理，提出在轮辋径向或周向开T型槽改进轮辋结构的方法，通过在T型槽内配上特定重量的T型螺栓实现对系统的真正补偿。结合理论计算和实际工况进行配平操作，试验结果表明，改进的轮辋结构和补偿方法较大程度地降低了系统自身不平衡量,为获得良好的信号源、消除信号干扰及降低系统磨损，得到更高的测试精度、稳定性和重复行提供了条件。

轮胎动平衡； 偏心补偿； 动态补偿； 轮辋； T型槽

引 言

轮胎动平衡试验机是轮胎行业内高精度的检测设备，其测试精度受诸多因素影响。不少企业、院校以及研究所对该试验机从理论和实践方面做了不少研究[1-9]，主要影响因素包括以下几个方面：a.机械结构的设计、加工和装配;b.传感器非线性、力的关联效应等的影响[10-12];c.复杂噪音背景下信号的调理、采集、滤波、幅值相位提取等各环节以及标定算法、偏心补偿算法和零校正算法[13-20]等;d.实际测试过程中，相关参数一致性和稳定性影响,如速度和压力的实时性[21]与稳定性、上下轮辋同轴度保证、轮辋与轮胎定中心臂同轴度保证、胎圈润滑程度、轮辋与轮胎装配误差以及轮辋宽度(段差)调节等。

驱动装置、传动系统以及主轴系的结构基本决定了系统的机械特性。良好的传动环节是测试速度恒定的保障，但传动过程中不可避免地会引入若干振动干扰。目前市面上的轮胎动平衡机主要采用皮带传动型，但实践发现皮带传动通常存在倍频信号干扰[22-23]。德国申克公司提出皮带浮动驱动装置，将皮带的单侧传动改为两侧传动。北京航空制造工程研究所625所为消除皮带干扰采用摩擦轮驱动,测试过程中摩擦轮脱开主轴，并加以速度补偿算法辅助的方式进行检测，但离心力对速度高度敏感。另外，设备长期运行对主轴机构配合精度也存在影响,主轴安装时要求全跳动不大于0.05，长期运行之后较难保证。系统自身偏心量的大小也决定了系统的检测精度[24]。系统自身偏心量大时，会引入较大的振动和噪声，使信噪比恶化，振动信号受到串扰，加剧主轴和轴承等关键结构的磨损，造成系统的不稳定，增加量标定次数，降低测试精度和效率。当待测轮胎的不平衡量较大时，易造成传感器的过载甚至损坏；当待测轮胎的不平衡量较小时，振动信号可能出现拍频现象，甚至畸形。所以，稳定且偏心量较小的测控系统是获得较高测试精度的基础和保障。当前的轮胎动平衡试验机大多不具备消除或减小系统自身偏心的装置或结构，试验机一旦安装完成，很少对系统自身的不平衡量加以配平，主要依靠安装过程中对关键部件单独动平衡来控制系统自身的不平衡量，而这种方法效果甚微。行业内轮胎动平衡试验机的偏心补偿操作，旨在每次测量解算时减去该偏心补偿结果以得到轮胎单独的不平衡量，并不具备真正补偿或配平系统偏心量的功能。文献[25]提出在旋转套筒上添加铅块的方法配平系统不平衡量。通过套筒的周向旋转可以满足任意角度配平的要求，但径向任意位置却实现不了。

综上所述，笔者基于现有的量标定和偏心补偿操作与算法，改进轮辋结构，改善偏心补偿操作流程，实现对系统自身不平衡量的真正补偿。

1 轮胎动平衡试验机的偏心量计算

每次的测量结果均包括了系统自身不平衡量和轮胎不平衡量两部分。求出试验机本身的不平衡量，并从测量结果中将其减掉，才能获得轮胎单独的不平衡量。知晓系统本身的偏心量，也是对系统进行配平的前提，可通过偏心补偿过程求解。偏心补偿主要是采用基2的整次幂反向消除法测量偶数次得到试验机自身的不平衡量。本试验系统中，偏心补偿过程共测量4次，则计算过程可表示为

(1)

(2)

(3)

(4)

系统自身不平衡量为

(5)

2 系统偏心的动态补偿

2.1 动态补偿轮辋的设计

基于原有的机械结构和轮辋尺寸，改进并得到了两种不同结构的轮辋。结合控制策略和补偿方法，可实现系统偏心量的动态补偿。图1所示的轮辋为正交式T型槽轮辋,在轮辋的正交方向上开4个T型槽，并配以特定尺寸的T型螺栓,T型螺栓作为配重，可在T型槽内移动并固定。图2所示的轮辋为环状T型槽轮辋,沿轮辋圆周方向开T型槽，同样配以槽内可移动的配套的T型螺栓。

轮辋层上均布的4个螺纹孔用于量标定过程中加载试重(砝码)。为了便于计算和信号处理，将砝码所在位置记为测试的0°位置，且就此建立坐标系xOy,如图3所示。理论上讲，轮辋层上任意位置均可设置正交的T型槽,而实际操作时，为了防止标定砝码和配重T型螺栓所在位置相干涉，使T型槽与xOy坐标轴有一定夹角γ。同时，在轮辋T型槽所在的正交方向构建坐标系x′Oy′。笔者开发的测试系统中，主轴呈顺时针方向旋转。图2中的环状T型槽轮辋则不需另设坐标系，且T型槽位置只需在轮辋直径方向避开量标定砝码加载孔即可。

图1 正交式T型槽轮辋Fig.1 Orthogonal T groove rim

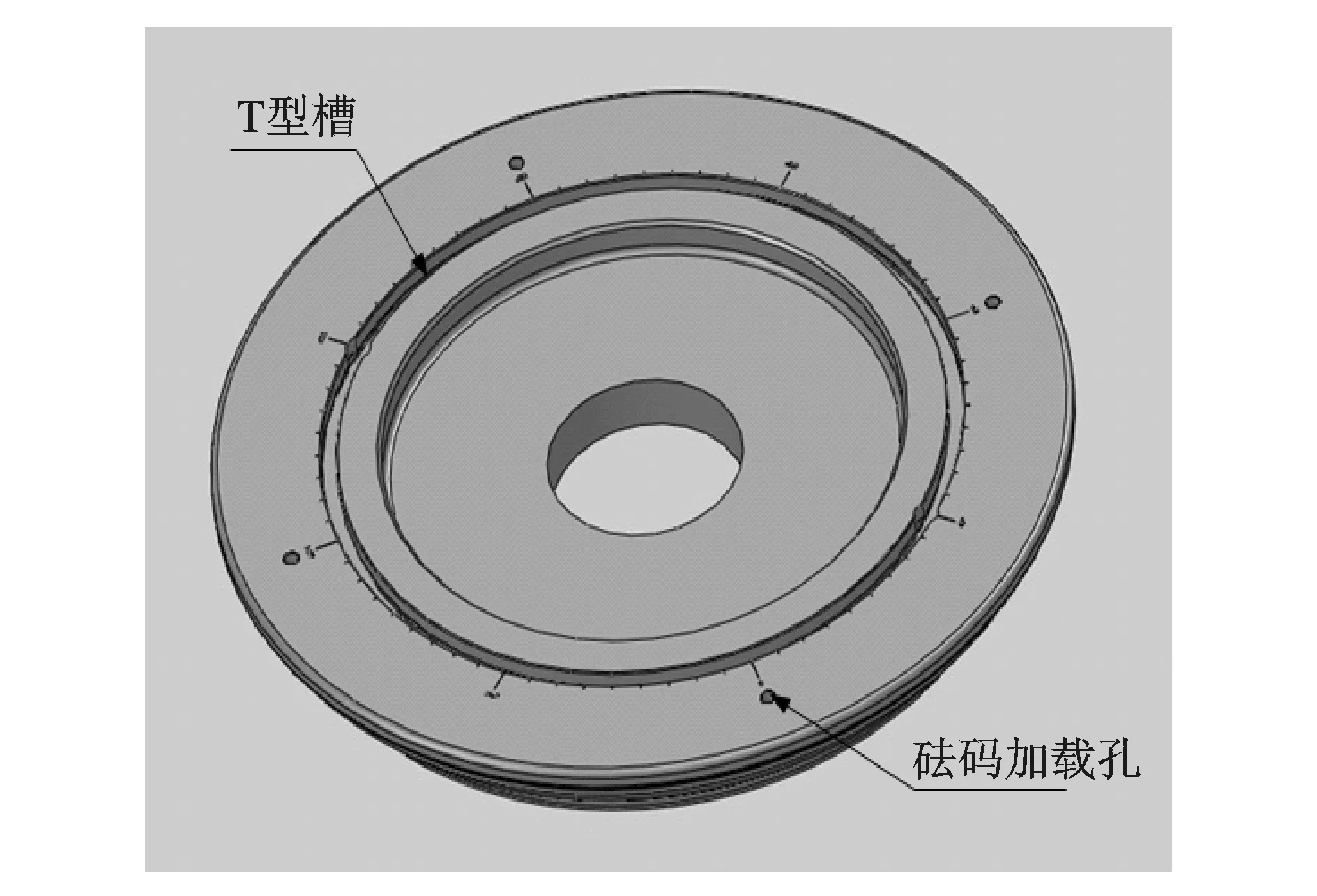
图2 环状T型槽轮辋Fig.2 Ring T groove rim

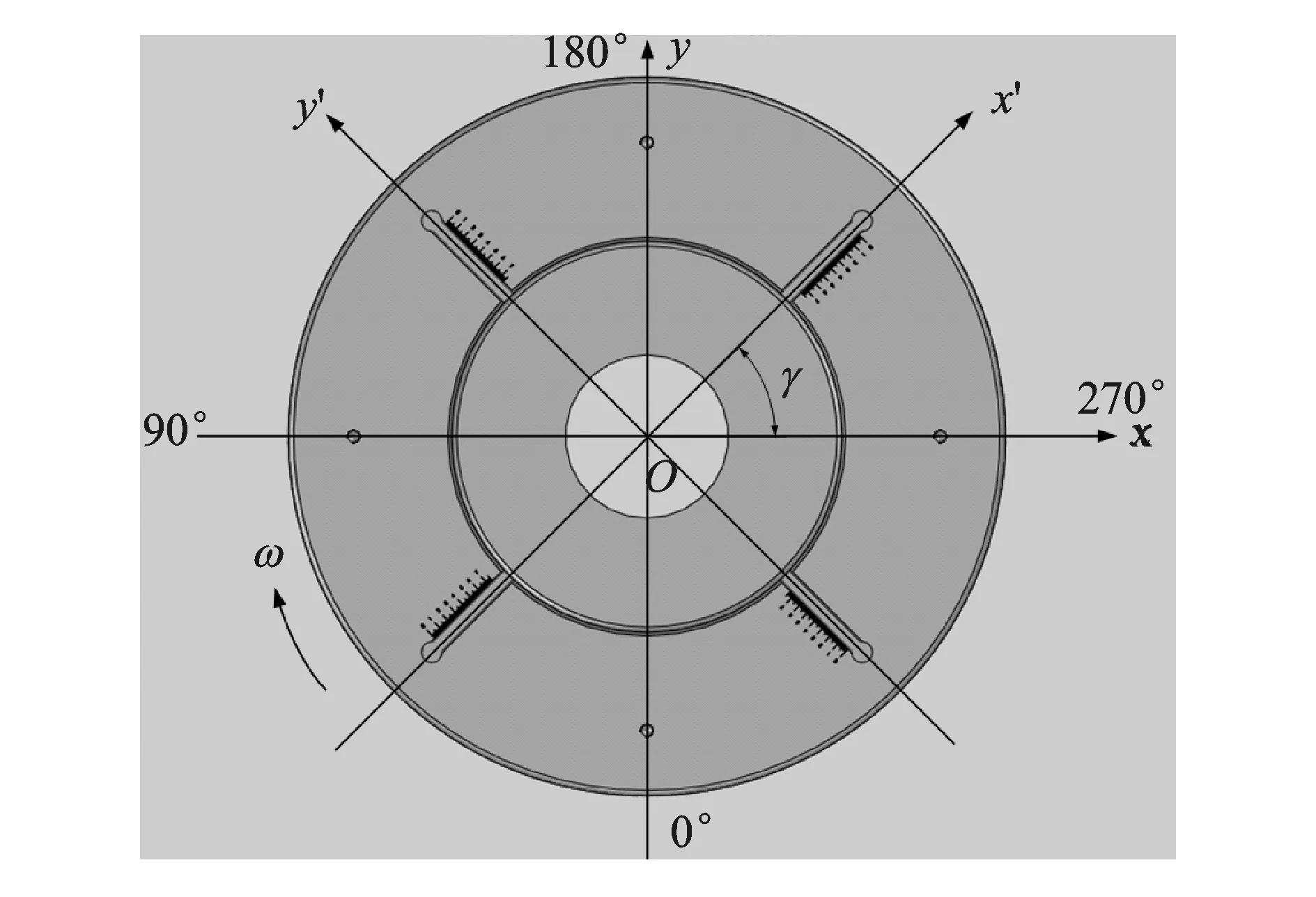
图3 坐标系分布图Fig.3 Coordinate distribution

2.2 系统不平衡量的动态补偿策略

设计算所得的系统自身上不平衡量为Mu(g)，角度为θ(°)；下不平衡量为Md(g)，角度为α(°)。由于解算所得的角度是系统不平衡量所在的重点位置，而实现配重功能的T型螺栓应该加在不平衡量的轻点位置,所以，设上下轮辋T型螺栓的加载位置为θ′和α′。当θ<180时，θ′=180+θ;当θ>180时，θ′=θ-180；α亦然。θ,α,θ′和α′都在xOy的测试坐标系内。

2.2.1 正交式T型槽轮辋配重策略

1) 测试坐标系与补偿坐标系重合。

当两坐标系夹角γ=0时，即测试坐标系xOy与补偿坐标系x′Oy′重合，则轮辋T型槽上应加的T型螺栓重量和位置为

(6a)

(6b)

(7a)

(7b)

其中：Mux和Muy分别为上轮辋x′轴和y′轴上应配平的T型螺栓的重量;Mdx和Mdy分别为下轮辋x′轴和y′轴上应配平的T型螺栓的重量；Lux和Luy分别为上轮辋T型槽内加载T型螺栓的位置；Ldx和Ldy分别为下轮辋T型槽内加载T型螺栓的位置；R为轮辋校正半径。

式(6)和式(7)均只讨论配平螺栓的大小，配平位置取Mu和Md所在象限相邻的T型槽即可。

2) 测试坐标系与补偿坐标系不重合。

当两坐标系夹角γ≠0时，即测试坐标系xOy与补偿坐标系x′Oy′不重合，则轮辋T型槽上应加的T型螺栓重量和位置为

(8a)

(8b)

(9a)

(9b)

本试验系统中取γ=45°。

采用正交式T型槽轮辋配平，可以把较大的配重分解成一对较小的配重加载到T型槽内，但是配重块的径向调整位置在某些机型下受轮辋结构限制。例如，图4所示载重轮胎使用的规格为R24.5-22.5-20的三级轮辋，为减轻轮辋重量和缩短上轮辋芯轴长度，轮辋中心通常使用下沉且挖空的结构形式。轮辋外直径为660 mm，内直径为400 mm，内直径以内均被掏空一定深度，且在轮辋中心开∅150 mm的孔用于与轮辋芯轴装配。出于安全考虑，T型槽外端与轮辋外缘预留10 mm。所以，该结构下正交式T型槽轮辋径向有效调整范围仅在200～320 mm内，很大程度上受到限制。但对于轿车轮胎或轻卡轮胎等较小或者较轻的轮辋，由于轮辋中心不掏空，所受限制较小，可以使用。

图4 轮辋尺寸示意图(单位:mm)Fig.4 The size diagram of the rim (unit: mm)

2.2.2 环状T型槽轮辋配重策略

采用环状T型槽轮辋不受轮辋直径影响，但是当系统偏心量较大时，配重也无法分解减小。另外，由于量标定过程中的校正半径和配平时的T型槽半径不同，所以需要将系统偏心量进行等效。

根据力矩平衡原理，有MR=M′R′，所以

(10)

其中：Mu为偏心补偿求出的系统不平衡量；Mu′为配重所用的T型螺栓重量；R为校正半径；R′为T型槽半径。

2.3 系统偏心动态补偿方法

根据不加配重时量标定和偏心补偿操作计算所得的Mux，Muy，Mdx，Mdy和Lux，Luy，Ldx，Ldy，在轮辋T型槽中调整T型螺栓的位置加以配平。配平后重新进行量标定和偏心补偿操作，得出配平后新的系统偏心量。如果理想即可停止配平，倘若系统偏心量依旧较大则可以重复以上过程，直至系统偏心降至可接受的理想范围为止。操作流程如图5所示，整个过程将得到越来越精确的标定系数和系统偏心量。

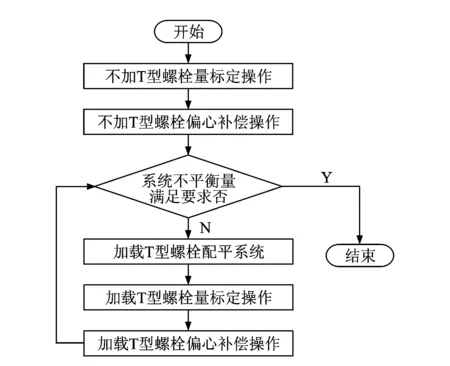
图5 动态配平操作流程Fig.5 Dynamic balancing operation process

3 试验结果对比分析

3.1 试验流程

3.1.1 正交式T型槽轮辋配平

使用规格为R24.5′-22.5′-20′的正交式T型槽轮辋，带上规格为295/80R22.5DSR266的轮胎进行偏心补偿操作。得到系统上下偏心量和角度为：上偏心量186.49 g(185.42°)；下偏心量265.65 g(312.78°)。由于T型螺栓应加载在系统不平衡量轻点上，故有

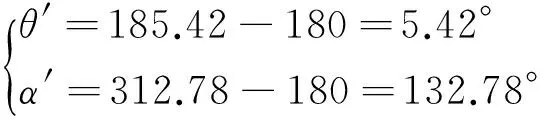
(11)

加载重量和位置计算如下

(12)

(13)

应在系统不平衡量轻点位置相邻的两T型槽,即-x′和-y′坐标系所在的T型槽内加载T型螺栓配平。在-x′槽的208 mm处加载132.83 g，-y′槽的 172.03 mm处加载130.90 g。但由于正交式T型槽轮辋径向有效调整范围为200～320 mm，所以172.03 mm实际操作受限。

此时，有以下调整方法：a.在-y′槽200 mm处加载130.90 g，之后重新标定和补偿，再次计算系统的偏心量，再次配平，直到系统偏心量降到理想范围;b.融合两种轮辋的配平方法,先按照环状T型槽轮辋等效方法，将系统自身偏心量从校正半径270 mm上等效到T型槽轮辋外端所在的圆周半径320 mm上，之后再采用正交T型槽轮辋配平方法进行分解后补偿。笔者采用第2种方法，故有

(14)

(15)

(16)

所以在-x′槽的246.66 mm处加载127.28 g，-y′槽的203.89 mm处加载100.26 g。

同理，对下轮辋进行配平操作，有以下几种方法：a.在-x′槽的10.46 mm处加载10.29 g，y′槽的269.80 mm处加载265.45 g； b.在-x′槽的8.58 mm处加载12.40 g，y′槽的319.76 mm处加载12.40 g。

3.1.2 环状T型槽轮辋配平

采用规格为R24.5′-22.5′-20′的环状T型槽轮辋带上3.1.1节中的轮胎进行偏心补偿操作，得到系统不平衡量为：上不平衡量178.95 g(190.33°);下不平衡量271.54 g(295.98°)。故有

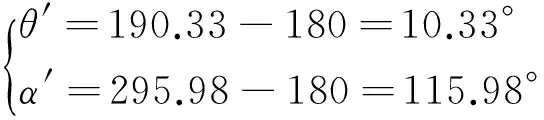
(17)

(18)

所以应该在上轮辋10.33 °处的T型槽内加150.99 g的螺栓，在下轮辋115.98 °处的T型槽内加229.11 g的螺栓。

分别使用正交式T型槽轮辋和环状T型槽轮辋对系统进行初次偏心测量，得出的系统自身不平衡量略有差别。这是因为系统自身的偏心量依赖于每一个组成部件，且不同轮辋的残余不平衡量不尽相同，所以一旦更换轮辋，系统偏心量会发生变化。此时，需要重新测量系统的不平衡量及重新补偿。

3.2 试验结果

分别使用不同的配平轮辋进行补偿后，得到配平前后系统偏心量对比结果如表1所示。补偿操作后，环状T型槽结构得到的系统偏心量较小，较正交式T型槽轮辋理想。

实际配平后仍残留系统偏心量,主要是因为实际的T型螺栓重量与理论要求的配重不完全一致，实际加载T型螺栓的位置与理论计算值有差异，偏心补偿操作本身存在测量误差等。但是，配重前后系统的偏心量已经降低至允许范围。

表1 配平前后系统偏心量对比结果

4 结 论

1) 引入改进后的轮辋结构和方法对系统进行配平补偿，能够将系统自身的不平衡量减小至理想范围。由于配平过程中T型螺栓的重量和加载位置以及测试误差等因素存在，系统偏心可能无法彻底去除。

2) 正交T型槽轮辋和环状T型槽轮辋都能起到配平效果,但考虑轮辋的实际工况，由于尺寸和结构限制，使用环状T型槽轮辋比较容易操作和实现。

3) 在实际工程中引入以上结构的轮辋，可以实现对系统自身不平衡量的真正补偿。对长期运行偏心量发生变化的系统也适用，起配重功能的T型螺栓可动态调整。

4) 减小系统自身的不平衡量，为获得较高的测试精度、稳定性和重复性奠定了基础。

[1] Lee H. Vehicle wheel and tire balance testing machine: US, 4193305[P]. 1980-03-18.

[2] David P, Richard L D, David P K, et al. Lateral load tire testing system: US, 7140242 B1[P]. 2006-11-28.

[3] Sigeru M, Kazuaki L. Apparatus for measuring uniformity and/or dynamic balance of tire: US, 6131455[P]. 2000-10-17.

[4] Jean E, Eric S, Jean-Marc B. Apparatus and method for measuring tire balance on a force variation machine: US, 6772626 B1[P]. 2004-08-10.

[5] Thomas D W, Steve H, Ronald J H, et al. Tire balancing apparatus: US, 7448267 B2[P]. 2008-11-11.

[6] 姜超浪. 全自动充气式轮胎动平衡试验机测控系统的开发[J]. 计算机测量与控制，2004, 12(6): 532-536.

Jang Chaolang. Development of tyre dymamic balance measuring machine [J]. Computer Measurement & Control, 2004, 12(6): 532-536. (in Chinese)

[7] 都强，杭柏林. 轮胎动平衡试验机及其控制系统[J]. 橡胶工业，2006，53(1): 41-45.

Du Qiang, Hang Bolin. The tire dynamic balanc test machine and the control system[J]. Rubber Industry, 2006，53(1): 41-45. (in Chinese)

[8] 刘迎澍，尹建华，巫上清.基于复影响系数的载重轮胎动平衡机标定算法[J].天津大学学报:自然科学与工程技术版，2013(6)：565-570.

Liu Yingshu, Yin Jianhua, Wu Shangqing. Complex influence coefficients based calibration algorithm of tire dynamic balanc testing machine[J]. Journal of Tianjin University: Science and Technology, 2013(6):565-570. (in Chinese)

[9] 杨静芳. 基于PLC的载重轮胎质量在线检测系统的研究与开发[D]. 济南：山东大学，2008.

[10]盖晓晶，赵继印，郑蕊蕊，等.轮胎三分力测量系统的研究[J].仪表技术与传感器，2006(8)：48-49.

Gai Xiaojing, Zhao Jiyin, Zheng Ruirui, et al. Study on tyre tri-component force measure sytem[J]. Instrument Technique and Sensor, 2006(8):48-49. (in Chinese)

[11]黄胜全. 加重面数大于测点数的转子平衡方法的研究[J].东北电力学院学报，2003,23(4)：63-64,74.

Huang Shengquan. Study on the balance of rotors on the number of ading the weight side large than that of measure sites[J]. Journal of Northeast China Institute of Electric Power Engineering, 2003,23(4):63-64,74. (in Chinese)

[12]王晓升. 测量点对转子动平衡影响的研究[J]. 西安交通大学学报， 1998，32(7): 85-89.

Wang Xiaosheng. Analysis of rotor balancing behavior as influrnsed by locations of data measurements[J]. Journal of Xi′an Jiaotong University, 1998, 32(7): 85-89. (in Chinese)

[13]牟世刚，冯显英，晏志文，等. 基于小波分析的动平衡机不平衡量提取方法研究[J]. 山东大学学报:工学版，2011, 41(3)：61-66.

Mu Shigang, Feng Xianying, Yan Zhiwen,et al. Study on unbalanced signal extraction from a dynamic balancing machine based on wavelet analysis [J]. Journal of Shandong University: Engineering Science, 2011, 41(3): 61-66. (in Chinese)

[14]都强，杭柏林. 最小二乘法在多传感器测量标定中的应用[J]. 传感技术学报，2005, 18(2): 244-246.

Du Qiang, Hang Bolin. Application of least squares in multisensor measure specifying [J]. Chinese Journal of Sensors and Actuctors, 2005, 18(2): 244-246. (in Chinese)

[15]Yang Jingfang, Feng Xianying, Fu Hongjun, et al. Research on calibration method of tire dynamic balance detection system[J]. Advanced Materials Research, 2012(542/543): 838-842.

[16]纪跃波. 弱非平稳转速下转子动平衡方法[J]. 振动、测试与诊断，2012,32(4)：596-601.

Ji Yuebo. Dynamic balancing of the rotor with weakly non-stationary rotational speed[J]. Journal of Vibration, Measurement & Diagnosis,2012,32(4):596-601. (in Chinese)

[17]李传江，费敏锐，张自强. 高精度动平衡测量中不平衡信号提取方法研究[J]. 振动与冲击，2012，31(14)：124-127.

Li Chuanjiang, Fei Minrui, Zhang Ziqiang. Method of unbalance signal extraction in high precision dynamic balancing measurement[J]. Journal of Vibration and Shock, 2012，31(14)：124-127. (in Chinese)

[18]杨世锡， 梁文军，于保华.振动信号多通道同步整周期数据采集卡设计[J].振动、测试与诊断，2013,33(1)：23-28.

Yang Shixi, Liang Wenjun, Yu Baohua. Design of vibration signal′s multi-channel integer period synchronous acquisition card[J].Journal of Vibration, Measurement & Diagnosis, 2013,33(1):23-28. (in Chinese)

[19]Pilkey W D, Bailer J, Smith P D. A computational technique for optimizing correction weights and axial location of balance planes of rotating shafts[J]. Journal of Vibration, Acoustics, Stress, and Reliability in Design, 1983, 105:90-93.

[20]万莉莉，张自强，李传江. 基于遗传算法的动平衡最小二乘影响系数法的优化[J]. 机械与电子，2010(4)：21-24.

Wan lili, Zhang Ziqiang, Li Chuanjiang. Optimization of least squre influence coefficient method based on genetic algorithm of rotor dynamic balance[J]. Machinery & Electronics, 2010(4):21-24. (in Chinese)

[21]杭柏林，高国威，蒋珍,等.轮胎动平衡试验机力多变量测量方法与同步逻辑的开发[J].石油化工设备，2011,40(4)：28-31.

Hang Bolin, Gao Guowei, Jiang Zhen, et al. Multi-variable measuring meathod and development of synchronous logical for the tyres dynamic balance instrumentaion[J]. Petro-Chemical Equipment, 2011,40(4):28-31. (in Chinese)

[22]王汉英.平衡机带传动的干扰振动分析[J]. 试验机与材料实验，1985，4：18-23.

Wang Hanying. The interference vibration analysis of the belt drive on balancing machine[J]. The Machine and Material Test, 1985, 4：18-23. (in Chinese)

[23]Yang Jingfang, Feng Xianying, Zhao Lianfang, et al. Influences of belt drive on the rotor balance detection system[ J]. Journal of Convergence Information Technology, 2012, 7: 672-679.

[24]毛伟杰. 动平衡机输出轴与实验部件之间偏心量对动平衡试验的影响[J]. 工程设计与建设， 2005，37(1)：26-28.

Mao Weijie. Effect of eccentricity between output shaft of dynamic balancing machine and parts to the tested on dynamic balancing results[J]. Engineering Design and Construction, 2005,37(1):26-28. (in Chinese)

[25]刘均，林钢. 轮胎动平衡测量中的主轴不平衡量测量方法及轮胎平衡机:中国,102072797 A[P]. 2011-05-15.

10.16450/j.cnki.issn.1004-6801.2016.03.014

*山东大学研究生自主创新专项基金资助项目(yzc12124)

2014-04-29；

2014-05-22

TH6

杨静芳，女，1985年10月生，博士生。主要研究方向为智能检测与数控技术。曾发表《Influences of belt drive on the rotor balance detection system》(《Journal of Convergence Information Technology》2012,Vol.7,No.3)等论文。

E-mail: longzhiyang @126.com