变截面杆中纵波传播特性的实验研究*

魏义敏， 杨世锡， 甘春标

(浙江大学机械工程学院 杭州，310027)



变截面杆中纵波传播特性的实验研究*

魏义敏， 杨世锡， 甘春标

(浙江大学机械工程学院 杭州，310027)

以往的理论研究结果表明，泊松效应和剪切变形对杆件中纵波的传播特性有着不可忽略的影响，纵波的传播特性也与杆件两端横截面面积比值的大小相关。为了对理论进行验证，搭建了实验系统并进行相关实验。实验结果表明：杆件材料的泊松效应、剪切变形使杆的截止频率变大；同时，变截面杆端面面积比值越大，截止频率越高。实验结果验证了以往的理论预测结果，帮助获取真实的振源振动信号，同时也为状态监测和降噪提供依据。

纵波； 变截面杆； 泊松比； 剪切变形； 传播特性

引 言

变截面杆是一种常见部件，振动在其中以波的形式进行传播。对于杆来说，波成分以纵波为主，其他类型的波通常可以忽略[1]。杆的振动问题牵涉到结构设计、力学及降噪等多方面的内容，往往伴随随机性、非均一性及噪声干扰等问题，实际工作情况复杂。波在通过杆等部件后，其成分可能会发生变化，在某些情况下，需要知道准确的振动信号来进行状态监测或者降噪。状态监测通常采用的是信号的幅值量等，同时，相位信号也可以提供丰富的信息[2-3]。杆等部件的振动会引起噪声，某些设备如舰船等对噪音有一定的要求，可以在噪音的传播路径上进行控制和抑制[4]。因此，有必要对变截面杆中纵波的传播特性进行研究。

变截面杆中弹性波传播特性研究一直受到国内外学者的关注，Krawczuk等[5]将杆的基本波动理论、Love理论以及Mindlin-Herrmann理论等几种波动理论进行了分析对比，并利用波数对纵波的传播特性进行了分析。皮钧等[6]根据回形变截面杆的结构特点和振动传播特性, 研究了纵波在变幅杆圆盘中发生的模态形式变化，并进行了实验。杨永军等[7]对波在输电线路中的传播特性进行了分析，得到了弹性波在输电线传播的群速度频散曲线，对不同的传播模态及频散特性进行了讨论。张再云[8]对弹性波在不同介质中的传播特性以及稳定性进行了研究。Guo等[9]对一组非均一杆中波的传播情形进行了研究，并对波在非均一杆传播时的截止频率进行了分析。Gaul等[10]采用基于能量的模型对杆与杆之间的耦合进行了研究，并进行了实验验证。Benatar等[11]对波黏弹性材料杆中相速度以及衰减进行了分析，并以某杆为例进行了实验验证。Mahata等[12]从实验的角度采用了不同的基于最小均方根的方法对黏弹性杆的弹性模量和泊松比进行了分析。对于纵波来说，影响其在变截面杆中传播的因素不仅包括杆材料的物理特性、杆的几何参数，也包括泊松效应、剪切变形等。

文献[13]基于基本波动理论、Love波动理论以及Mindlin-Herrmann波动理论，对杆材料的泊松比、剪切变形以及截面变化方式、端面面积比进行了分析研究，并且利用有限元方法进行了仿真分析，发现泊松效应和剪切变形的影响不可忽略，同时杆两端横截面面积比越大，变截面杆的截止频率越高。笔者在此基础上，搭建实验台，分析纵波传播时的幅值和相位等传播特征，对文献[13]的理论分析和有限元仿真的结果进行进一步的验证。

1 理论介绍

研究纵波在变截面杆中的传播特性时，通常假设杆内所有点的运动均为简谐运动。首先，利用基本波动理论、Love波动理论以及Mindlin-Herrmann波动理论，对杆内的点进行分析，求出杆的运动方程；其次，建立杆的传递矩阵；然后，对传递矩阵进行分析，求解其特征值，分析纵波向前传播时的幅值和相位特点；最后，推知纵波在变截面杆中的传播特性。

1.1 运动方程的建立

图1为变截面杆的示意图，杆的横截面面积沿着中性轴变化。基本波动理论中，假设杆上所有的点只进行纵向运动，因此只存在纵向位移，并且位于同一垂直于中性轴的横截面上，所有的元素具有相同的位移。Love波动理论认为，由于泊松效应，杆上的每一个点除了纵向运动，还同时存在一个径向速度[5]。

图1 变截面杆示意图Fig.1 A schematic of a rod with variable cross-section

(1)

如果令γ=0，则式(1)即为由基本波动理论推导得出的运动方程。

由于泊松效应，杆上的任一点不仅存在纵向位移，还具有一个径向速度。事实上，这个径向速度还将进一步导致每个点具有独立的剪切变形。在Love波动理论的基础上考虑剪切变形即为Mindlin-Herrmann理论[5]。假设杆上所有点的运动为简谐运动，则有u(x,t)=U(x)eiωt,ψ(x,t)=Ψ(x)eiωt。其中，ψ(x,t)为剪切变形。由Mindlin-Herrmann理论推导得出的杆的运动方程[13]为

(2μ+λ)A(x)U(x),xx+(2μ+λ)A(x),xU(x),x+

λA(x),xΨ(x)+λA(x)Ψ(x),x=

-ρA(x)ω2U(x)

(2)

(3)

其中：I(x)=∫A(x)r2dA；μ=E/(2(1+γ))；λ=γE/((1+γ)(1-2γ))。

1.2 传播特性

上面给出了3种不同波动理论下变截面杆的运动方程，根据运动方程可以对传播特性做进一步分析。通常，杆上所有点的运动状态可以通过状态向量Y=[φuMV]T来表示，其中：φ，u，M，V为广义物理量，这些广义物理量一般是位移、斜度、力和力矩等。如图1所示，设纵波从变截面杆的某一位置O开始传播，通过变截面杆传播到位置S处，该传播过程可以写成

YS=TYO

(4)

其中:T为传递矩阵。

传递矩阵T的特征值就包含了波的传播特征信息[14]。设T的特征值为λi，λi可以写成指数次幂的形式

(5)

其中：μi为传播常数；αi为衰减因子，反应了波传播过程中的幅值信息；βi为相位角，反应了波在传播时的相位信息。

如果某频段内波成分相位角为0或者±π，则表示该波成分在向前传播时与反射的波相遇并且相互抵消，该波成分不能通过该介质，该频段称为阻带；反之，波成分能够通过的频率范围称为通带；通带和阻带的临界频率称为截止频率，文中用ωc来表示。

建立传递矩阵时，对基本波动理论和Love波动理论来说，通常选取[UU,x]T为传递矩阵的基向量，而对Mindlin-Hermann波动理论来说，通常选用[UΨU,xΨ,x]T作为传递矩阵的基向量。对传递矩阵T的特征值进行求解，就可得知纵波的传播特性。可以求出，由基本波动理论推知的纵波的传递矩阵的特征值为

(6)

(7)

可以求出，由Love波动理论推知的纵波的传递矩阵的特征值为

(8)

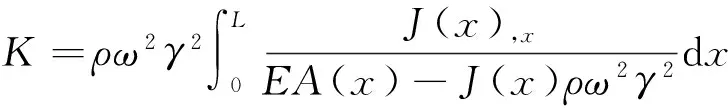
由式(8)可知，特征值是否存在非0虚部，主要取决于指数中的根号项的运算结果。如令(P-K)2-4ρω2LW≥0，则λ1,2只有实部，虚部为0。对不等式进行化简求解并且考虑到ω≥0，因此，杆的截止频率为

(9)

频率低于ωc的波成分，将不能通过变截面杆；而频率高于ωc的波成分则可以通过。同样可以得出，变截面杆中纵波传播时的阻带为[0，ωc]。由式(9)可知，截止频率不仅与杆材料的物理参数有关，同时也与杆两端面截面积比值的大小相关，M越大，ωc越大。

可以求出，由Mindlin-Herrmann理论推导的传递矩阵的特征值为

(10)

(11)

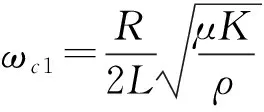
(12)

同样可得，变截面杆中纵波传播时的阻带为[0，ωc]。由式(12)可知，杆的截止频率不仅与杆本身有关，也与杆两端面截面积比值的大小相关。截面面积变化越大，则截止频率也越大。

3种波动理论推导得出的通带、阻带以及截止频率均不相同，需要对其进行分析研究，以确定何种理论更适合用来分析纵波的传播特性。

2 实验系统设计及可行性分析

2.1 实验内容及实验系统设计

实验内容设计为两个部分：a.验证变截面杆是否存在截止频率，泊松效应和剪切变形是否存在影响；b.验证截止频率与杆截面面积的变化方式以及杆端面面积比的关系。选用2根截面面积变化方式不同的变截面铝杆以及1根等截面铝杆作为实验对象，见图2。首先，通过变截面杆与等截面杆的对比分析，研究变截面杆的截止频率；然后，通过不同变截面杆的对比分析，分析截面变化方式对传播特性的影响。2根变截面杆为指数变截面杆A(x)=A0e0.693 1x/L和多项式变截面杆A(x)=A0(1+2x/L)0.630 9，变截面杆端面的宽度保持不变，高度随着x的变化而变化。两变截面杆端面面积A0均为0.02 m(宽)×0.02 m(高)，杆长度L相同且均为1 m。对于这两种变截面情形来说，均满足A(L)=2A(0)。等截面杆的端面尺寸为0.02 m(宽)×0.028 9 m(高)，其长度也为1 m，与指数变截面杆具有相同体积。由机械手册可以查得，铝的密度为2.7×103kg/m3，弹性模量为72.7×109Pa，泊松比为0.3。

图2 变截面杆Fig.2 The rods with variable cross-section

实验系统以隔振台为基座，由杆、支撑架、力锤、加速度传感器、数据采集系统以及其他附件组成，如图3所示。实验系统中，2个支撑架安装在隔振台上，杆通过连接在支撑架上的橡皮绳被悬挂在支撑架上。力锤用来敲击杆的端面，模拟纵波的产生。加速度传感器安装在杆的另一端，可以测量出杆的纵向加速度。信号采集系统用来采集力锤和加速度传感器的信号，并对数据进行本地存储。实验时，力锤敲击杆的小端，模拟产生入射的纵波，纵波产生后，便沿着杆的方向向前传播，当纵波传播到大端后，此时纵波的信号会被加速度传感器所获取。与此同时，信号采集系统从力锤敲击开始，同步采集力锤以及加速度传感器的信号，并进行本地存储。在获取力锤和加速度传感器的数据后，就可以对其进行分析，对纵波在变截面杆中的传播特性进行研究。

图3 实验系统框图Fig.3 A schematic of the experiment setup

2.2 实验的可行性分析

进行理论分析时，杆模型边界条件为双端自由，且纵波已经在杆中向前传播。因此，实验中也需要使杆的边界条件为双端自由，产生纵波，并且让其沿杆进行传播。此外，为了对纵波进行分析，还需要数据采集系统对纵波信号进行精确采集，便于后续分析。

实验系统中，2个支撑架被固定在隔震台上，支撑架并没有和杆直接接触，而是通过橡皮绳进行弹性连接,如图4所示。由于橡皮绳具有良好的弹性，且在进行实验时，杆的运动位移小，可以近似认为杆的运动状态未受到橡皮绳的影响，杆的自由度保持不变。因此，可以认为两端悬挂的支承方式满足双端自由的边界条件。

图4 支撑架Fig.4 The support frame

实验系统中选用的力锤自带传感器，敲击时可以输出力的大小信号。力锤配有4种不同材质的锤头，分别是钢锤头、铝锤头、尼龙锤头以及橡胶锤头，每种锤头敲击时产生的信号频率范围均不同。实验中选取了尼龙锤头，如图5所示。尼龙锤头激发的信号频率，可以覆盖本研究中通带、阻带的频率范围，力锤在实验中用来敲击杆的端面，模拟纵波的产生。

图5 力锤Fig.5 The force hammer

力锤敲击杆端面后，纵波沿着杆向前传播，当纵波传播到另一端时，会被安装在端面的加速度传感器所获取，实验中选用的加速度传感器的量程为0～100g，可以满足测量需求，如图6所示。数据采集系统选用了LMS数据采集系统，它由数据采集器以及采集器上位机两部分组成，如图7所示。该数据系统采样频率最高可达204.8 kHz，并且可以对多个通道进行同步采集及分析，能够满足对纵波的采集和分析要求。

图6 加速度传感器Fig.6 The acceleration sensor

图7 LMS数据采集系统Fig.7 The LMS data acquisition system

通过以上分析可知，本实验系统满足了理论分析时的相关条件，可以用来研究变截面杆中纵波的传播特性。

3 实验与理论分析对比

3.1 理论分析结果

第1节推导出了3种波动理论下纵波的传播常数以及截止频率，将第2节中变截面杆的相关参数相应地代入式(6)、式(8)、式(10)和式(11)，便可以绘制纵波在变截面杆中的传播常数图。由于指数变截面方式和指数变截面杆传播常数结果相同，笔者仅给出了指数变截面杆的传播常数图，如图8所示。图8给出了衰减因子以及相位角和波成分频率的对应关系，从图中可以看出，相位角从“零”变为“非零”的转折点和衰减因子的转折点对应。从截止频率的定义可知，该点对应的频率即为截止频率。相位角为零时，表示对应的波成分与反射回来的波成分相遇，相互抵消，无法通过杆进行传播。变截面杆具有类似“低通滤波器”的特性，处于阻带频带范围内的波成分无法通过，这一特性可以加以利用来对“噪声”进行抑制，也为状态监测提供了依据。

图8(a)中由基本波动理论推导得出的阻带为[0,260]，截止频率为260 Hz；图8(b)中由Love波动理论推导得出的阻带为[0,280]，其截止频率为280 Hz；图8(c)中，由Mindlin-Herrmann理论推导的截止频率为[0,340]，截止频率为340 Hz。从阻带的大小上看，泊松效应和剪切变形对传播特性的影响不可忽略。

图8 理论分析得出的传播常数图Fig.8 Propagation constants deduced from the theoretical analysis

3.2 实验结果与分析

实验中，分别对指数变截面杆、多项式变截面杆以及等截面杆进行多次实验，并完整记录了所有实验的数据。利用力锤进行敲击时，存在以下两种情况：a.力度过大或者过小，力度过小，传感器输出信号信噪比低，不利于分析；力度过大，传感器会发生过载；b.重复敲击，在敲击时存在2次或者多次敲击的现象，力锤的信号出现2个或者多个峰值，对分析结果不利。上述情形下的实验数据，不能作为实验结果分析的数据。

力锤在每次敲击时，敲击力度可能不一样，因此，笔者在对实验数据进行分析时，以力的大小为依据，选取了5组锤击力范围在80～100 N之间的实验数据进行分析。分析结果表明，尽管5组数据的时域信号不一样，但是所求得的通带、阻带以及截止频率偏差很小，误差控制在5%以内。现以其中的一组为例进行分析说明。

图9为经过归一化以后力锤的时域信号图以及快速傅里叶变换(fast Fourier transform,简称FFT)。由图可看出，力锤的时域信号有效长度为0.001 s，其能量分布主要集中在频率范围[0,2 000]内，该范围包含了杆的截止频率，可以用来进行传播特性的研究。

图9 力锤信号分析Fig.9 Analysis for the signal of the force hammer

通过实验发现，指数变截面和多项式变截面的杆，所得出的分析结果一致，以指数变截面杆为例给出了实验分析结果。实验中数据采集器采集了加速度传感器以及力锤的信号值，对这些响应信号进行时频分析，就可以得知纵波的传播特性。结合各种时频方法的分析特点及实际效果，笔者采用了短时傅里叶变换(short time Fourier transform,简称STFT)来进行时频分析。通常，不能直接对响应完整的时域信号进行分析，因为其中包含了大量的反射波成分以及其他的干扰成分，需要对时域响应进行适当的截取[13]。在对信号进行截取时，信号长度如果过长，虽然频率分辨率很高，但纵波可能已经发生多次反射；若长度过短，频率分辨率太低，无法对理论的结果进行验证。因此，此处截取了前0.02 s的时域信号进行分析。0.02 s的信号长度，对应的频率分辨率可达50 Hz，虽然其中仍包含少量的反射成分，但分析发现反射成分未对分析结果造成明显影响。

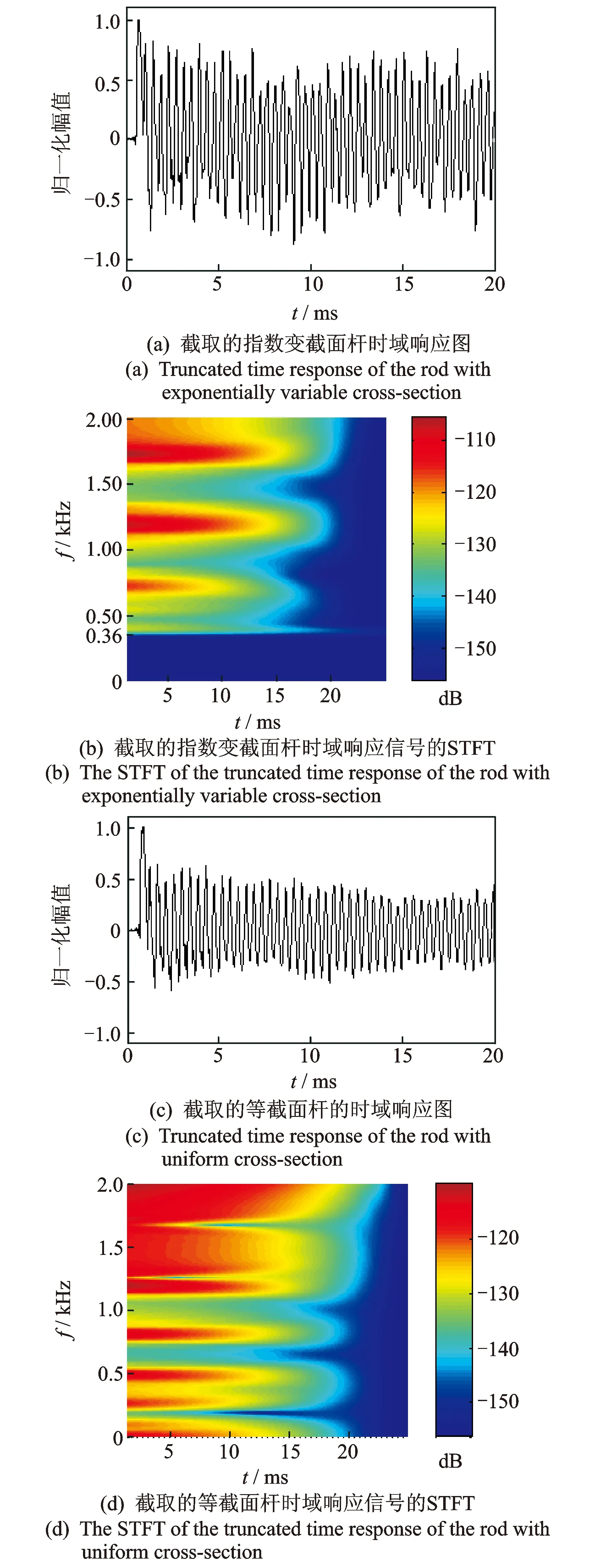
图10 指数变截面杆和等截面杆实验结果分析Fig.10 Comparison between the experimental results from the rods with exponentially variable cross-section and with uniform one

图10(a)为截取的指数变截面杆的响应时域信号，信号长度为0.02 s；图10(b)为与图10(a)对应的STFT图；图10(c)为截取的等截面杆的响应时域信号，信号长度为0.02 s；图10(d)为与图10(c)对应的STFT图。通过图10(b)和(d)的对比，发现变截面杆在频率范围[0,360]内没有能量分布，说明没有波成分存在，因此可以认为，变截面杆确实存在阻带、通带以及截止频率。可以看出，该频率范围与由Mindlin-Herrman理论推导得出的阻带吻合，说明剪切变形和泊松效应对纵波的传播有着不可忽略的影响。

此外，等截面杆可以看成一种特殊的端面面积比为1的指数变截面杆。从理论分析和实验结果可知，其截止频率为0，而变截面杆A(x)=A0e0.693 1x/L，端面面积比为2，截止频率为360 Hz。实验结果表明，杆两端横截面面积比越大，截止频率越大。

4 结 论

1) 实验结果表明，相较于基本波动理论和Love理论，由Mindlin-Herrmann理论模型得出的阻带与实验最为吻合，因此可以认为，剪切变形和泊松效应对纵波的传播有着不可忽略的影响，同时也验证了理论分析结果的正确性。

2) 变截面杆截止频率与截面面积变化方式无关，但与杆两端横截面面积的比值有关，且横截面面积比值越大，截止频率越高。这一实验结论也与理论预测结果相吻合。

3) 变截面杆具有类似“低通滤波器”的特性，这一特性帮助了解真实的振源振动信号，有利于进行状态监测以及降噪等。

[1] Doyle J F. Wave propagation in structures[M]. 2nd. New York: Springer, 1997:172-184.

[2] 吴昭同,杨世锡.旋转机械故障特征提取与模式分类新方法[M].北京:科学出版社,2012:1-5.

[3] 高品贤,苏燕辰,伍川辉.基于振动信号相位特性的状态监测[J].振动与冲击,2009(8):188-190,194.

Gao Pinxian, Su Yanchen, Wu Chuanhui. Equipments condition monitoring based on phase characteristic of vibration signal[J]. Journal of Vibration and Shock, 2009(8):188-190,194. (in Chinese)

[4] 曹跃云,张磊,杨自春,等.船舶振动噪声源传递路径分析及试验验证[J].振动与冲击,2013,32(22):158-162.

Cao Yueyun, Zhang Lei, Yang Zichun, et al. A new OPA model for ship noise sources and test validation[J]. Journal of Vibration and Shock, 2013,32(22):158-162. (in Chinese)

[5] Krawczuk M, Grabowska J, Palacz M. Longitudinal wave propagation. part I: comparison of rod theories[J]. Journal of Sound and Vibration, 2006,295(3/4/5):461-478.

[6] 皮钧,纪跃波.纵波回形变幅杆的研究[J].振动、测试与诊断,2010,30(1):65-69.

Pi Jun, Ji Yuebo. Study on longitudinal vibration of a folded acoustic horn[J]. Journal of Vibration, Mesurement & Diagnosis,2010,30(1):65-69. (in Chinese)

[7] 杨永军,李华东,裘进浩.弹性波在高压输电线中的传播特性[J].振动、测试与诊断,2012,32(2):214-217.

Yang Yongjun, Li Huadong, Qiu Jinhao. Propagation characteristics of elastic wave in the overhead transmission cable[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(2):214-217. (in Chinese)

[8] 张再云.弹性波在不同介质中的传播及其稳定性分析[D]. 长沙：中南大学,2011.

[9] Guo Shuqi, Yang Shopu. Wave motions in non-uniform one-dimensional waveguides[J]. Journal of Vibration and Control, 2012,18(1):92-100.

[10]Gaul L, Bischoff S, Sprenger H, et al. Numerical and experimental investigation of wave propagation in rod-systems with cracks[J]. Engineering Fracture Mechanics, 2010,77(18):3532-3540.

[11]Benatar A, Rittel D, Yarin A L. Theoretical and experimental analysis of longitudinal wave propagation in cylindrical viscoelastic rods [J]. Journal of the Mechanics and Physics of Solids, 2003,51(8):1413-1431.

[12]Mahata K, Mousavi S S, Derstr M T. On the estimation of complex modulus and Poisson′s ratio using longitudinal wave experiments [J]. Mechanical Systems and Signal Processing, 2006,20(8):2080-2094.

[13]Gan Chunbiao, Wei Yimin, Yang Shixi. Longitudinal wave propatation in a rod with non-uniform cross-section[J]. Journal of Sound and Vibration, 2014,333(2):434-445.

[14]Sheng Xiaozhen, Li Minghua. Propagation constants of railway tracks as a periodic structure[J]. Journal of Sound and Vibration, 2007,299(4-5):1114-1123.

10.16450/j.cnki.issn.1004-6801.2016.03.015

国家自然科学基金资助项目(11172260，11372270，51375434)；高等学校博士学科点专项科研基金资助项目(20110101110016)；浙江省科技计划基金资助项目(2013C31086)；中央高校基本科研业务费专项资金资助项目(2013XZZX005)

2014-04-16；

2014-06-19

TH113.1

魏义敏，男，1986年6月生，博士生。主要研究方向为机械部件中弹性波传播机理。曾发表《Longitudinal wave propagation in a rod with non-uniform cross-section》(《Journal of Sound and Vibration》2014，Vol.333,No.2)等论文。

E-mail：yiminwei@126.com