基于张量黎曼度量的序列图像匹配光流场计算方法

杨欢， 沈晓军， 李杰， 吴政隆， 徐蓓蓓

(1.北京理工大学 机电学院，北京 100081；2.中国人民解放军63961部队，北京 100012)



基于张量黎曼度量的序列图像匹配光流场计算方法

杨欢1， 沈晓军2， 李杰1， 吴政隆1， 徐蓓蓓1

(1.北京理工大学 机电学院，北京 100081；2.中国人民解放军63961部队，北京 100012)

使用序列图像的灰度-时空张量描述子来描述图像特征，并在此基础上提出了一种基于张量黎曼度量的序列图像匹配光流场计算方法. 该方法使用张量的黎曼度量给出序列图像特征描述子间距离的定义，并使用改进的Hausdorff距离取代欧式距离来完成黎曼度量的计算，据此构造序列图像匹配相关函数，以提高图像在噪声及遮挡情况下的匹配能力；在上述基础上，给出匹配光流场算法. 仿真结果显示，该算法相对于传统基于微分的光流场计算方法(H-S算法，L-K算法)和传统的基于灰度的块匹配算法在计算精度、抗噪声等方面更有优势.

黎曼度量；匹配光流场；图像匹配；Hausdoff距离；灰度-时空张量描述子

光流法是一种简单实用的图像运动的表达方式，通常定义为一个图像序列中的图像亮度模式的表观运动[1]. 光流场的传统计算方法包括微分法和匹配法. 微分法比较具有代表性的是由Horn和Schunck提出的古典光流约束方程[2]. 基于微分法计算光流场事实上是基于前后两帧对应像素点亮度无变化这一理想的假定条件，因此当灰度值发生突变或运动速度较大时，此类方法的计算误差将急剧增加，并不再满足上述假设条件[3].

所谓基于块的光流方法，是将图像区域分隔成互不重叠的小区域，并且对每一个块内的运动使用一个简单的参数模型进行特征化，并借此估计块运动矢量的方法，这种算法通常称为块匹配算法(blocking matching algorithm, BMA). Berger K等[4]提出了一种基于块匹配的稀疏光流场的计算方法，Mac A O等[5]提出了一种利用时空张量检测光流场计算置信度的方法. Liu C等[6]提出了一种SIFT Flow计算方法，该方法基于光流的计算框架，通过提取图像中每个像素处的 SIFT 特征来替代像素值，从而得到两幅图像间致密的，点对点的对应关系来描述目标的运动场. Colored SIFT(CSIFT)[7]提出在颜色不变空间构建 SIFT 描述子，以取代灰度空间表征输入图像. 与传统的SIFT Flow相比，对颜色和光照更加鲁棒. 在文献[3]中，还描述了一种基于灰度正规化相关的光流场计算方法，并给出了光流可信度的评价准则.

传统基于匹配方法的最大问题在于，有多种情况可能导致模板不能正确匹配，其原因主要为：① 小模板内信息较少；② 正确的匹配点可能无法获得最高的匹配度. 由于图像的背景信息中往往含有大量的对称纹理，因此在使用相关性分析方法进行匹配时，往往存在多峰性，从而导致正确的匹配点难以获得.

针对上述问题，作者提出了一种基于张量黎曼度量的序列图像匹配光流场计算方法，该方法使用灰度-时空张量描述子代替传统匹配方法中的灰度信息来描述图像信息，并使用基于黎曼度量的Hausdorff距离构造匹配相关函数，完成图像中特征的匹配，进而获取图像匹配光流场. 本文最后的仿真结果显示，相较于传统基于微分的光流场计算方法和块匹配光流场计算方法，该算法可以获得更加准确和稳定的图像匹配光流场.

1 序列图像的灰度-时空张量描述

序列图像I(x，y，t) 可以看作一个关于x，y和t的三维张量，如图1所示，其中x，y两维是二维图像的空间维，t是序列图像的时间维. 对于图像上任意一点，其结构张量可定义为

(1)

式中：*为卷积运算；Ix，Iy分别为图像在x，y方向的偏导数；G为尺度是σ的高斯函数. 上述结构张量仅仅描述了单帧图像在梯度上的信息，联合图像灰度和图像在x，y，t3个维度上的梯度信息，构建结构张量，T=G*ffT=

式中：f=[IIxIyIt]，I为图像在(x，y)处的灰度；Ix，Iy分别是图像在x，y方向的偏导数. 该结构张量包含了图像上任意一点的灰度和梯度信息，将其称为图像的灰度-时空张量描述子.

2 结构张量的黎曼度量

对于图像上每一个点，都按照式(2)的结构张量进行展开，其本身就可构成一个流形空间. 结构张量间的距离度量一般不使用欧氏距离，如图2所示，采用流形空间两点的测地线距离来对其进行度量，即图中虚线所示.

使用小写字母表征向量空间中的点，如x∈Rm，其对应的位于黎曼流形上的点使用大写字母表示，如X∈M，TX为流形上过点X的切平面，d(X，Y)表示流形上两点X，Y间的距离. 设y∈TX，X∈M，从X点出发，存在唯一一条指向点Y的测地线γ，其在向量空间TX的投影为向量y，使用指数映射算子(exponentialmappingoperator)可将切向量y从向量空间映射到流形空间. 如图2所示，其在流形空间里的映射即是测地线的终点，则测地线的长度可写为

(3)

(4)

则根据文献[10]，测地线距离可写成，

(5)

3 基于改进Hausdorff距离的匹配相关函数构造

基于模式的匹配法需要构造相关性函数. 传统基于灰度的匹配使用形如式(6)作为相关性函数[3]，C=

(6)

对于给定的两个点集T={t1，t2，…，tn}和P={p1，p2，…，pm}，T和P两个点集间的经典Hausdorff距离定义为[11]

(7)

其中，

(8)

(9)

经典Hausdorff距离的问题在于其对于干扰非常敏感，当两个点集中即使有一点(又称为外点)相差较大，也会带来比较大的计算误差，为了增强算法鲁棒性，目前有两种常用的改进算法：CHD算法和MHD算法. 这里采用LTS-HD算法，该算法的思路是将CHD和MHD算法结合起来，构造Hausdorff距离如(10)(11)所示，

(10)

(11)

式中，类似于部分Hausdorff距离，H=f*NA，f∈(0，1]，表征了升序排列的数据序列dt(p)和dp(t)前H个值. 同样的，当f=1时，式(10)和(11)退化成MHD算法.

由式(10)(11)，匹配相关系函数可构造为

(12)

式中，各个像素点使用式(3)的结构张量来表征，dM为张量的黎曼度量，则式(12)可以写为

(13)

式中tm，n，pi，j分别为模板和待匹配图像上的像素点的结构张量.

4 基于灰度-时空张量描述子的块匹配光流场算例与分析

4.1 计算精度分析

源图像采用Yosemite序列的第1帧和第2帧图像，如图3所示，图像尺寸为320×240. 这个图像序列中，左下侧的山谷在向外侧做扩张运动，上方的乌云在向右侧做平移运动，同时伴随比较剧烈的光照变化.

在配备Intel core P8750处理器的计算机上，在Matlab 2012b平台下，使用本文所述算法，进行光流场计算. 分别选用8×8，16×16和32×32的模板进行匹配计算，得到的基于灰度-时空张量的匹配光流场如图4(a)～4(c)所示.

使用式(14)的算法，对于图5中各点的计算误差进行分析，计算4(a)、4(b)、4(c)光流场相对于5(d)标准光流场的平均角误差(RAAE)和相对标准差(RSTD)，统计了其计算时间为

(14)

式中：wSt为Horn算法计算的光流矢量；w为本算法计算的光流矢量.

作为对比，分别使用HS算法和LK算法计算全局光流场，同时计算了基于灰度的块匹配光流场，模板大小为8×8，光流场计算结果如图5(a)～5(c)所示. 与标准光流场相对比，统计这几种方法与本文算法的误差和计算时间，见表1.

表1 使用本文算法及传统算法计算Yosemite序列光流场误差及计算时间

Tab.1 Error and computing time of methods with different template sizes

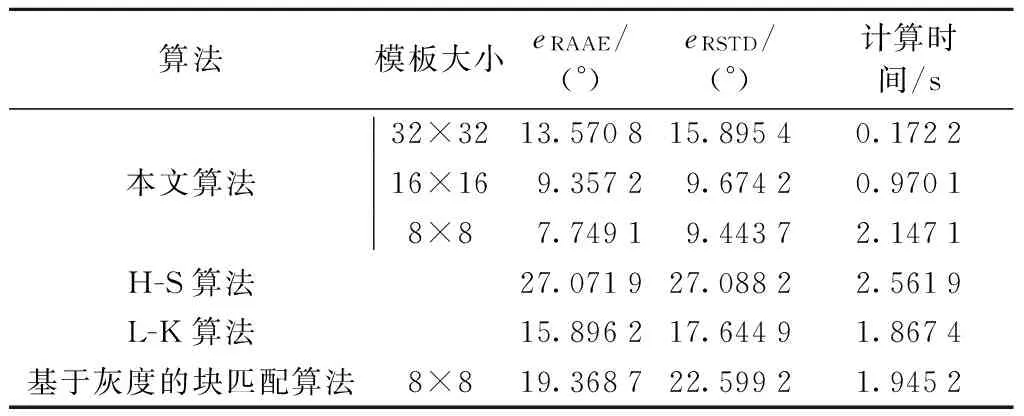
算法模板大小eRAAE/(°)eRSTD/(°)计算时间/s32×3213.570815.89540.1722本文算法16×169.35729.67420.97018×87.74919.44372.1471H-S算法27.071927.08822.5619L-K算法15.896217.64491.8674基于灰度的块匹配算法8×819.368722.59921.9452

从上述仿真结果可以看出，相比传统的微分方法以及匹配光流场计算常用的基于灰度匹配的方法，本文提出的方法在精度和计算效率上都具有一定优势，同时具有一定的光照变化适应性，在工程应用中，可以考虑采用16×16或32×32等较大匹配模板，可以在计算精度和计算效率方面获得一种折中.

4.2 抗噪声能力分析

基于灰度-时空张量描述的图像相比于传统基于灰度描述的图像，在抗噪声性能方面具有一定的鲁棒性，对于图4所示的图像序列添加高斯噪声，测试其在噪声环境下的计算精度. 待测试图像序列共分为3组，分别添加均值为0，方差为0.01，0.05和0.10的高斯白噪声.

使用本文所述的算法，计算上述3种情况下的光流场，匹配模板选用16×16，计算结果如图6(a)～6(c)所示.

同样与标准光流场相对比，统计上述结果的角误差，如表2所示.

作为对比，同样使用H-S算法，L-K算法和基于灰度的块匹配对图4序列进行计算，噪声水平为E=0，D=0.01， 获得光流场如图7所示， 与标准光

流场相比，其计算误差见表3.

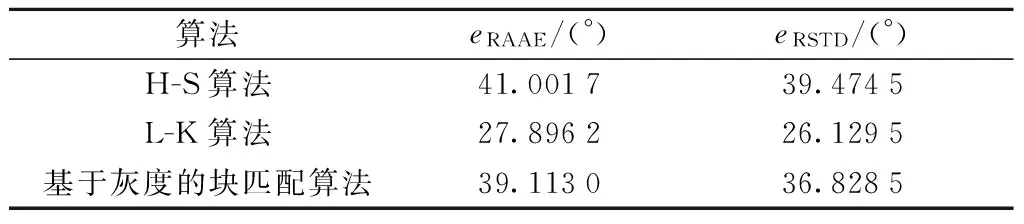
表3 几种其他算法计算Yosemite序列光流场误差对比

综上，可以看出，本文提出的算法在噪声环境下相比传统的光流算法，具有更高的计算精度，即使采用较大模板，在光照变化不剧烈的区域，也有不错的计算结果.

5 结 论

提出了一种基于灰度-时空张量描述子(grayscale-space-time tensor descriptor， GSTTD)的块匹配光流场计算方法. 该方法首先使用灰度-时空张量描述子对序列图像的特征进行描述，并通过指数映射，将灰度-时空张量描述子映射到流形空间中，提出了一种基于黎曼测度的灰度-时空张量描述子距离，并在此基础上改进Hausdorff距离，提出一种基于黎曼度量的图像匹配算法. 在此匹配算法的基础上，提出了基于灰度-时空张量描述子的块匹配光流场算法，并进行了相关数值实验，分析了该算法的精度和抗噪声能力. 仿真结果表明，该算法的精度优于传统的基于微分的算法(H-S，L-K等)和基于灰度的块匹配算法，且可以通过调整匹配模板大小控制算法的速率；进行的抗噪实验表明，该算法抗噪能力同样优于上述传统算法.

[1] Beauchemin S S， Barron J L. The computation of optical flow[J]. ACM Computing Surveys (CSUR)， 1995，27(3):433-466.

[2] Horn B K， Schunck B G. Determining optical flow[J]. Artificial Intelligence, 1981,17:185-203.

[3] 徐晶，方明，杨华民. 计算机视觉中的运动检测与跟踪[M].北京:国防工业出版社，2012.

Xu Jing， Fang Ming， Yang Huaming. Motion detection and tracking in computer vision[M]. Beijing: National Defense Industry Press， 2012. (in Chinese)

[4] Berger K， Kastner M， Schroeder Y， et al. Using sparse optical flow for two-phase gas flow capturing with multiple kinect[M]∥[S.l.]: Computer Vision and Machine Learning with RGB-D Sensors. Springer International Publishing， 2014:157-169.

[5] Mac A O， Humayun A， Pollefeys M， et al. Learning a confidence measure for optical flow[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2013，35(5):1107-1120.

[6] Liu C， Yuen J， Torralba A. Sift flow: dense correspondence across scenes and its applications[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33(5):978-994.

[7]Abdel-Hakim A E， Farag A A. CSIFT: A SIFT descriptor with color invariant characteristics[C]∥Proceedings 2006 IEEE Computer Society Conference on. Computer Vision and Pattern Recognition. [S.l.]: IEEE， 2006，2:1978-1983.

[8] Tuzel O， Porikli F， Meer P. Human detection via classification on riemannian manifolds[C]∥Proceedings CVPR’07 IEEE Conference on Computer Vision and Pattern Recognition. [S.l.]: IEEE， 2007:1-8.

[9] Pennec X， Fillard P， Ayache N. A Riemannian framework for tensor computing[J]. International Journal of Computer Vision， 2006，66(1):41-66.

[10] Förstner W， Moonen B. A metric for covariance matrices[C]∥Geodesy-The Challenge of the 3rd Millennium. [S.l.]: Springer Berlin Heidelberg， 2003: 299-309.

[11] Huttenlocher D P， Klanderman G A， Rucklidge W J. Comparing images using the Hausdorff distance[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1993，15(9):850-863.

(责任编辑：刘雨)

Matching Optical Flow Field Computing Method Based on Riemannian Metric of Tensor

YANG Huan1， SHEN Xiao-jun2， LI Jie1， WU Zheng-long1， XU Bei-bei1

(1.School of Mechatronical Engineering， Beijing Institute of Technology， Beijing 100081， China;2.63961 Unit of the PLA， Beijing 100012， China)

Taking the grayscale-time-space tensor descriptor (GTSTD) as a feature descriptor of image sequence, a matching optical flow computing method was presented based on Riemannian metric of tensor. Riemannian metric of tensor was used to measure the distance of features, while an improved Hausdorff distance was used to replace traditional Euclidean distance in the computing Riemannian metric, forming a correlation function of image match to enhance the matching ability of the algorithm in the case of noise and occlusion. Based on all above, the matching optical flow computing algorithm was given out. Simulation results show that this method has advantage on accuracy and noise immunity compared with method based on differential algorithm (H-S, L-K) and block matching algorithm based on grayscale.

Riemannian metric； matching optical flow field； image match; Hausdorff distance; grayscale-time-space tensor descriptor

2014-11-14

国防“十二五”基础科研重点项目(B2220132013)

杨欢(1992—)，女，博士生，E-mail:yanghuan@bit.edu.cn.

沈晓军(1959—)，男，研究员，E-mail:sxj_1959@126.com.

TP 242.6

A

1001-0645(2016)08-0862-06

10.15918/j.tbit1001-0645.2016.08.016