基于软件接收机的标量与矢量跟踪算法设计与分析

2016-11-23曾广裕申强董宇光李淼

北京理工大学学报 2016年8期

曾广裕，申强，董宇光，李淼

(1.北京理工大学机电工程与控制国家级重点实验室，北京 100081;2.中国航天电子技术研究院空间电子工程中心，北京 100094；3.中国北方工业公司，北京 100053)

曾广裕1，2，申强1，董宇光3，李淼1

以Matlab软件接收机为平台，研究对比了标量与矢量跟踪算法结构原理及算法设计，并分析了两种不同算法在信号短暂遮挡环境下的接收机跟踪性能. 建立了基于扩展卡尔曼滤波的矢量延迟/频率锁定跟踪算法模型，分析了矢量跟踪算法控制过程及时间同步问题，分析了标量与矢量跟踪算法在信号短暂遮挡环境下快速重跟性能及其对定位的影响，并进行了半实物仿真. 仿真结果表明，矢量跟踪算法不仅具有更好的快速重跟性能，而且接收机的位置检测精度和位置检测平滑度都优于标量跟踪算法.

软件接收机；矢量跟踪；标量跟踪；全球导航卫星系统(GNSS)

GNSS卫星定位接收机信号跟踪的目的是使接收机复制的本地载波及伪码信号与接收到的卫星载波及伪码相位保持一致，以剥离接收信号中的载波及伪码信息. 常规GNSS接收机常采取基于锁相跟踪原理的基带信号处理方法，对于不同跟踪通道分别设置了独立的载波及伪码跟踪环. 然而，该跟踪策略忽略了卫星与接收机间的运动共性信息，因此也存在接收机动态冗余性能有限，且信号重跟时间长等不足[1]. 基于该原则，早在20世纪80年代，由Spilker J J等[2]首次提出了矢量跟踪的概念，与此对应，将常规接收机跟踪环路称为标量跟踪. 矢量跟踪过程中，载波及伪码相位信号的跟踪及接收机位置、速度、加速度等状态信息的检测通过单独的中心卡尔曼滤波器以矢量方式实现. 常见的矢量跟踪实现方式有基于位置状态信息与基于伪距状态信息两种不同结构[1]. 位置状态信息中，卡尔曼滤波状态量为接收机位置、位置相关衍生量及接收机时钟信息；伪距状态信息中，状态量为伪距及与伪距相关的衍生量.

由于软件接收机具有较硬件接收机更多的潜在优势，如：灵活性，便于新算法的开发与实现；软件模块可重复性强等. 文章以参考文献[3]中研究的Matlab软件接收机为平台，研究对比了标量跟踪算法与基于位置状态信息的矢量跟踪算法的结构原理及其算法实现，分析了两种不同算法在信号短时遮挡环境下接收机跟踪性能，并进行半实物仿真验证，为矢量跟踪算法的研究提供理论指导.

1 标量跟踪算法及其定位原理

1.1 标量跟踪结构模型及其优缺点

标量接收机基带信号处理过程中，对不同通道输入信号，分别设置独立的Costas环及DLL延迟锁定环以完成对输入信号载波及伪码序列的跟踪. 信号跟踪过程中，接收机以捕获得到的载波及伪码相位信息作为信号跟踪过程中本地NCO初始值，将本地NCO生成的载波及伪码信息与输入信号混频，经积分清除后，分别得到I/Q支路即时(IP，QP)、超前(IE，QE)、滞后(IL，QL)相关累加值，通过对相关累加值的鉴频/鉴相，获取本地NCO与输入信号载波及伪码相位误差，并将获取得到的载波及伪码相位误差信息经环路滤波器后转换为本地NCO调整量，利用锁相跟踪原理实现对跟踪环路的闭环控制，如图1所示.

标量跟踪算法在高载噪比(C/N0)及低动态环境下具有良好的跟踪性能[1]. 然而，该方式同样存在许多缺陷：① 对于不同信号强度输入信号，接收机采取相同且固定的噪声带宽，常规跟踪算法难以实现对不同强度输入信号的权衡；② 若通道卫星被遮挡，接收机无法利用其余通道信息实现对遮挡通道的辅助跟踪，信号遮挡通道载波及伪码参数将处于随机发散状态；③ 常规接收机设计方案中不同通道信号跟踪环路各自独立，忽略了卫星与接收机间的运动共性信息，因此也存在接收机动态冗余性能有限，且信号重跟时间长等不足.

1.2 标量跟踪定位原理

标量跟踪算法常采取“伪距定位原理”，接收机通过获取4颗或者4颗以上卫星相对接收机伪距位置关系，通过解算伪距方程完成对接收机位置状态信息的检测.

伪距ρ(t)定义为信号接收时间tu(t)与信号发射时间ts之间差异与真空中光速c的乘积，即

(1)

式中τ为信号实际传播时间.

(2)

式中：r为接收机相对卫星间真实距离；I(t)为电离层延迟；T(t)为对流程延迟.

因此，伪距ρ(t)可表示为

(3)

式中：δtu为接收机时钟误差；δts为卫星时钟相对GPS时误差；ξP为其他误差项.

由式(1)(3)可知，为了获取不同时刻接收机相对卫星间伪距ρ(t)关系，最重要的是获取精确的信号发射时间ts. 硬件设计中，不同卫星信号发射时间tsi将通过对导航电文的解调及对应时刻锁相跟踪过程中伪码相位信息cp的组装获取，如图2所示.

与硬件接收机信号发射时间ts获取方式不同，软件接收机信号处理过程中将定位时间统一至信号发射时刻，如图3所示，其中，虚线为不同卫星信号发射时刻，右边黑实线为接收到的不同通道卫星信号相对信号发射时刻的时间延迟. 由图3可知，各通道接收信号时间延迟除包含约70 ms共同时延部分外，各通道卫星间仍存在时延相互关系δti，1，该时延相互关系可通过各通道帧同步后，由帧同步起始点位置关系获取.

图4为软件接收机定位原理示意图. 假设接收机掌握着一定精度的本地时钟tu(t)，tu(t)=tu+δtu，其中tu为本地时钟准确值，δtu为本地时钟偏差，则本地时钟减去信号传播延迟(约70 ms)可作为某个接收通道上的卫星信号发射时间.

假设1号卫星距离地面最近，该颗卫星发射信号到达地面时间最早，因此，1号卫星信号发射时间ts1(t)可表示为

(4)

式中：δt1为信号传播延迟估算误差；δt=δt1+δtu，由信号传播延迟时间估算误差及接收机本地时钟绝对误差组成.

同样，其余通道卫星信号发射时间tsi(t)可统一表示为

(5)

式中δti，1为第i号卫星与第1号卫星信号发射时间偏差值，为常量.

因此，若接收机同时跟踪4颗或者4颗以上卫星信息，则式(3)所示的伪距方程为

cδt=70c+I+T，

(6)

各通道间信号传播延时δti，1为常量. 通过对式(6)的求解实现对接收机位置状态信息的获取.

2 矢量跟踪算法

2.1 矢量跟踪模型及其优缺点

与标量跟踪算法不同，矢量跟踪过程中，载波及伪码相位信息的跟踪及接收机位置、速度、加速度等状态信息的检测将通过中心扩展卡尔曼滤波器EKF(extended Kalman filter，EKF)以矢量方式实现. 其基本原理是利用码相位和载波频率的预测误差直接修正用户的PVT(position/velocity/time)信息，然后将修正后的用户PVT反馈给本地复制信号生成器，生成新的码相位和载波频率的预测值，实现环路的闭环控制. 图5为典型矢量延迟/频率锁定环VDFLL结构原理[4].

矢量VDFLL跟踪算法以接收机位置、速度、加速度、接收机钟差、钟漂等信息为状态量，为了降低运算量，扩展卡尔曼滤波估计的是状态量误差而非状态量本身，并且用估计的状态量误差信息校正导航输出[5].

定义误差向量Xe=

式中，前面9项分别是估计的接收机位置、速度、加速度在地心地固(ECEF)坐标系下的误差值，后2项分别为估计的接收机钟差及钟漂误差值.

状态向量的选取可根据实际应用接收机动态需求选定，对于低动态场景，可忽略接收机自身加速度等信息的干扰，从而降低状态量维数，降低滤波器设计难度. 由牛顿运动学规律，系统状态转移方程为

(7)

即

式中：T为卡尔曼滤波更新时间；Wk为均值为0、协方差为Q的过程噪声.

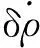
(8)

式中:Vk为均值为0，协方差为R的噪声项，噪声协方差R的统计值不仅与伪码相位及载波频率鉴别器类型有关，同时也与信号强度有关[7]. 由于测量噪声R中包含了接收机各通道的伪码误差及载波频率误差噪声项，假设各通道的码相位误差以及载波频率误差间不相关，则R为对角阵，其对角线元素大小与实际接收到的信号强度有关，当卫星信号受到干扰或者遮挡时，实际的噪声项会发生较大变化. 因此，矢量VDFLL跟踪处理中，为提高接收机抗干扰性能及滤波性能，须实时估算出不同时刻接收信号噪声特性并调整R的变化.

由于矢量跟踪算法综合利用了不同通道卫星与接收机间相互关系，有着较标量接收机更多潜在的优势[7-11]:① 扩展卡尔曼滤波器EKF能更好地权衡各通道伪码相位及载波频率误差值，通过实时检测不同通道噪声特性，EKF能提供最优的接收机位置、速度等状态信息，具有更优良的动态冗余性能；② 由于矢量跟踪方式能更好地权衡卫星与接收机以及接收机信号通道间信息的关联性，因此，矢量跟踪具有更优良的微弱信号检测跟踪性能；③ 具有良好的快速重跟性能及信号幅值快速起伏波动下信号跟踪的潜能.

2.2 矢量跟踪控制模型及控制流程

VDFLL算法实现主要基于两基本原则：伪码相位变化基于接收机位置的改变；载波多普勒频移基于接收机速度的变化.

矢量跟踪过程中，伪码及载波鉴相器检测获取k+1时刻输入信号与k时刻本地复制信号残差，并作为扩展卡尔曼滤波观测量. 扩展卡尔曼滤波将估算得到的接收机位置误差状态信息更新接收机位置状态信息，将修正后的接收机位置状态信息与k时刻卫星轨道信息，获取对应时刻伪距及伪距率变化量，并以此调整本地NCO，实现对环路的闭环控制，如图6所示. 图7给出了矢量跟踪算法滤波控制流程.

2.3 矢量跟踪算法时钟同步过程

矢量跟踪过程中，为保证伪距及伪距率残差控制在鉴别器牵入范围内，接收机需获取一定精度的初始位置、速度及时钟等状态信息，如标量跟踪引导. 由于时钟同步问题涉及到处理信号的时间参考点及该时间参考下各通道状态信息，如通道载波频率信息、伪码相位信息及对应时刻卫星轨道信息. 实际应用中矢量软件接收机仍可采取与软件标量跟踪算法相类似时钟同步策略，如图8所示.

矢量跟踪各通道以标量跟踪结束后帧同步时刻为起点，不仅确保了各通道卫星都具有相同的tow时，而且各通道都具有相位误差为0的初始伪码相位值.

3 半实物仿真验证

半实物仿真由GNSS7700思博伦卫星信号模拟器生成一组信号短时遮挡环境下的静态场景数据，各通道卫星信息如表1所示. 仿真过程中，设置8号卫星在启动模拟器25 s后中断5 s再重新恢复，用以验证本文提出的矢量跟踪算法的正确性与合理性以及对遮挡信号的快速重跟性能.

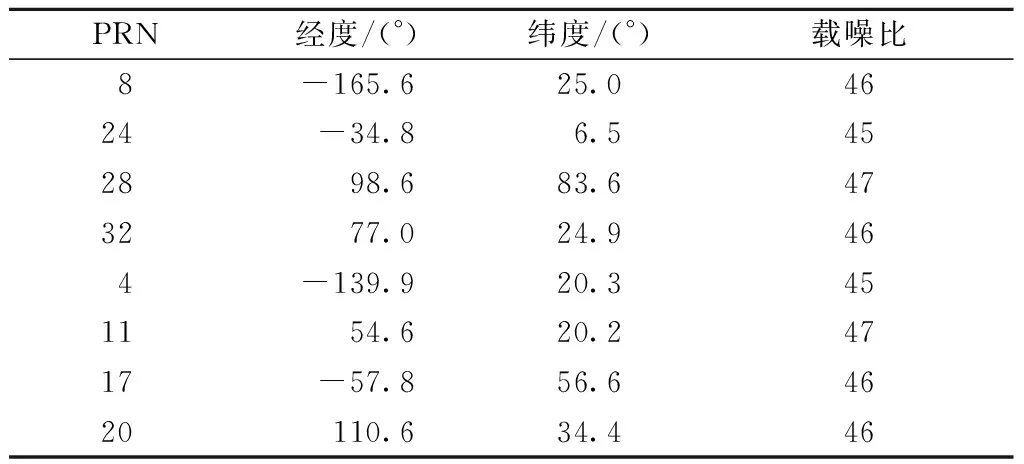
表1 卫星信息

验证过程以Matlab软件接收机为平台，将模拟器输出的静态场景卫星信号经NS210B卫星中频采集器采集并转换为软件接收机可识别的二进制数据源. NS210B中频采集器输出中频4.123 9 MHz，采样频率16.368 MHz. 矢量VDFLL跟踪前，经标量跟踪获取矢量VDFLL相关初始值，如不同卫星信号发射时间、接收机初始位置等信息并通过解算星历文件方式获取不同时刻卫星轨道信息. 图9为由标量转入VDFLL跟踪时刻，标量跟踪获取到的星空可视卫星分布效果图，与模拟器生成场景相吻合.

为了更好地分析矢量跟踪对短时遮挡通道信号的跟踪性能，以标量跟踪为对比，环路参数设置如下：载波锁相环带宽8 Hz，伪码延迟锁定环带宽2 Hz，并采取载波环辅助码环跟踪策略. 仿真过程中，选取4，8，11，17，24，28六通道卫星进行VDFLL跟踪，EKF更新率为20 ms. 矢量VDFLL跟踪过程中，选取归一化超前减滞后功率法伪码鉴相策略以及叉积鉴频策略实现对输入信号与本地生成信号伪码相位及频率偏差的估计. 参考文献[11-12]分别给出了两种不同鉴别策略测量噪声协方差R的估算方法，过程噪声Q中包含接收机位置、速度、加速度及时钟误差相关噪声，这些项可以通过接收机运动状态，本地时钟精度等先验信息进行预设.

图10为标量与矢量VDFLL跟踪算法跟踪8号卫星伪码鉴别器输出图. 由图10可知，矢量跟踪算法由于综合利用了各通道间相互关系，当通道信号短暂遮挡时，通道状态信息如通道载波及伪码相位信息仍可通过其余正常通道，由扩展卡尔曼滤波预估获取，从而保证通道在信号恢复时刻仍能快速实现跟踪. 而标量跟踪算法由于通道间的相关独立，信号丢失时载波及伪码NCO处于随机游走状态，无法利用其余通道信息的辅助快速实现对失锁通道的锁定跟踪.

图11为矢量跟踪算法跟踪8号卫星估算得到的伪距率、伪距及载噪比与模拟器实际输出值对比效果. 由图11可知，即便出现通道信号丢失，丢失信号通道状态信息仍可利用其余通道信息进行辅助跟踪，并正确预估出信号丢失环境下通道卫星与接收机间伪距及伪距率变化值.

图12为标量跟踪算法与矢量跟踪算法位置检测效果图，其中，标量跟踪与矢量跟踪算法位置状态输出更效率分别为2 Hz与50 Hz. 表2为SDLL与VDFLL定位误差统计表. 由图12及表2可知，无论是从定位误差均值还是均方值角度，矢量跟踪有比标量跟踪更优良的位置检测精度. 然而，由矢量VDFLL定位曲线可知，随着通道信号的丢失，对应通道噪声的增加也一定程度上影响了矢量跟踪定位性能，存在通道间信息互扰等问题，其鲁棒性较标量差.

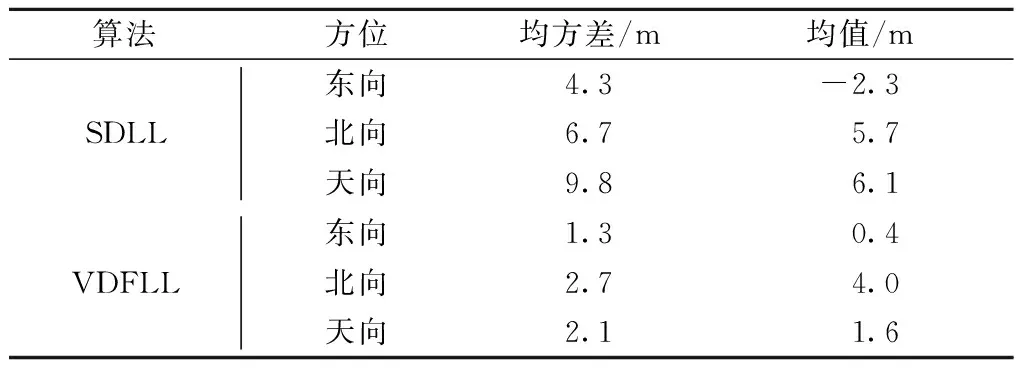
表2 VDFLL与SDLL定位误差统计表

4 结论

研究对比了基于Matlab软件接收机为平台的标量与矢量跟踪算法的区别及其算法实现，并对比分析了两种不同跟踪算法对短暂遮挡信号的快速重跟性能及其定位性能. 半实物仿真结果表明，矢量跟踪算法不仅具有更优良的快速重跟性能，而且无论是接收机位置检测精度还是位置检测平滑度都优于标量跟踪算法.

[1] Matthew L，David M.Comparison of traditional tracking loops and vector based tracking loops for weak GPS signals[C]∥Proceeding of ION GNSS 20th International Technical Meeting of the Satellite Division.Texas：IONGNSS, 2007：866-875.

[2] Spilker J J.Vector delay lock loop processing of radiolocation transmitter signals: United State Patent 5398034[P].1995-03-14.

[3] Borre K， Akos D A， Bertelsen N， et al. A software-defined GPS and Galileo receiver: a single-frequency approach[M]. Boston: Birkhauser Boston Inc， 2007.

[4] Matthew L， David M. A valid comparison of vector and scalar tracking loops[C]∥Proceedings of IEEE/ION Position Location and Navigation Symposium Conference. Indian Wells/Palm Spring， USA: IEEE， 2010:464-474.

[5] Matthew L，David M.Vector delay/frequency lock loop implementation and analysis[C]∥Proceedings of International Technical Meeting.Anaheim:[s.n.]，2009:1073-1086.

[6] 曾广裕，申强，李东光，等.基于扩展卡尔曼滤波的全球导航卫星系统矢量跟踪建模与仿真[J].兵工学报，2015，36(3)：530-538.

Zeng Guangyu， Shen Qiang， Li Dongguang， et al. Modeling and simulation on GNSS vector tracking loop based on extended Kalman filter[J]. Acta Armamentarii， 2015,36(3):530-538. (in Chinese)

[7] 罗雨，王永庆，罗海坤，等.基于扩展卡尔曼滤波器的矢量跟踪算法研究[J].电子与信息学报，2013，35(6):1400-1405.

Luo Yu， Wang Yongqing， Luo Haikun, et al.Study on vector tracking loop based on extended Kalman filter[J]. Journal of Electronics & Information Technology， 2013，35(6):1400-1405. (in Chinese)

[8] Matthew L， David M. What are vector tracking loops and what are their benefits and drawbacks[J]. GNSS Solution Column，IEEE/ION，2006，4(3)：44-53.

[9] Matthew L， Bevly David M. Analysis of discriminator based vector tracking algorithms[C]∥Proceedings of the 2007 National Technical Meeting of The Institute of Navigation.[S.l.]: ION-AM， 2007:570-576.

[10] Thomas P，Bernd E.Use of a vector delay lock loop receiver for GNSS signal power analysis in bad signal conditions[C]∥Position，Location and Navigation Symposium. [S.l.]: IEEE/INO，2006:893-903.

[11] Nazia K， Heikki H， Jari N. Vector tracking loop design for degraded signal environment[C]∥Ubiquitous Positioning Indoor Navigation and Location Based Service(UPINLBS). [S.l.]: IEEE, 2010：1-4.

(责任编辑：刘雨)

Design and Analysis of Scalar and Vector Tracking Algorithms Based on Software Receiver

ZENG Guang-yu1，2， SHEN Qiang1， DONG Yu-guang3， LI Miao1

(1.National Key Laboratory of Science and Technology on Electomechanical Dynamic Control， Beijing Institute of Technology， Beijing 100081， China; 2.Chinese Aerospace Electronic Technology Research Institute, Space Electronic Engineering Center， Beijing 100094， China;3. China North Industries Corp， Beijing 100053， China)

In this paper, the structure theory and algorithm design between scalar and vector tracking algorithm were studied and compared based on the Matlab software receiver, and the tracking performances of the two different algorithms were analyzed under temporary shelter environment. Firstly, the scalar structure and its position principle were analyzed; secondly, a vector delay/frequency lock tracking algorithm model was developed based on extended Kalman filter, and the control process and time synchronization of vector tracking was analyzed. Finally, the rapid re-tracking performance between VDFLL and SDLL tracking algorithm and its influence on the positioning were analyzed. Semi-physical simulation results show that the vector tracking algorithm has better performance on rapid re-tracking and both the accuracy and the smoothness of the position detection are better than the scalar tracking.

software receiver； vector tracking； scalar tracking； global navigation satellite system (GNSS)

2014-08-12

国家部委预研项目(40404020402)

曾广裕(1986—)，男，博士生，E-mail:zengguangyu1986@163.com.

申强(1977—)，男，博士，副教授，E-mail:bit82shen@bit.edu.cn.

TN 966

1001-0645(2016)08-0800-07

10.15918/j.tbit1001-0645.2016.08.006