一类非负张量谱半径的上下界

李海龙

(吉林工程技术师范学院应用理学院，吉林 长春 130052)

非负张量是非负矩阵的重要推广，关于其特征值和特征向量有许多研究结果[1-7].张量的特征值问题有重要的应用背景，如在盲源分离[8]、磁共振成像[9-10]、分子构象[11]等方面都有重要应用.本文利用张量的有向图，研究一类非负张量谱半径的上下界，其结果改进了此类非负张量谱半径上下界估计的相应结论.

1 基本定义和定理

如果ai1i2…im≥0，称为非负张量.

2005年，Qi[12]和Lim[1]分别定义了张量的特征值.

定义1对于m阶n维张量和一个向量x=(x1，x2，…，xn)T，xm-1是一个向量，其第i个分量为

(

一个复数λ称为张量的特征值，如果存在一个非零向量x=(x1，x2，…，xn)T，使得

类似于非负矩阵理论，我们称ρ()=sup{|λ|:λ∈spec()}是张量的谱半径，其中spec()是张量的特征值集合.

文献[13]将不可约矩阵的概念推广到张量.

定义2[13]对于m阶n维张量，如果存在一个非空的真子集I⊂〈n〉，使得

ai1i2…im=0， ∀i1∈I， ∀i2，…，im∉I，

对于m阶n维张量=(ai1i2…im)，记G=(V(G)，E(G))是伴随于张量的有向图，其结点集合V(G)=〈n〉，有向边集合E(G)={(i，j):aii2…im≠0，j∈{i2，…，im}}[14-15].如果对每一对i，j∈V(G)(i≠j)都存在由i到j和由j到i的有向路径，则称G是强连通的.我们定义G上的简单回路集合为C(G)，G上包含平凡回路的循环回路集合为定义

文献[5]给出了如下非负张量的特征值和特征向量的结果：

定理1[5]如果=(ai1i2…im)是m阶n维非负张量，则存在λ0≥0和一个非负向量x0≠0，使得

(1)

文献[5]又进一步证明了

定理2[5]如果=(ai1i2…im)是m阶n维不可约非负张量，则方程(1)中的(λ0，x0)满足：

(ⅰ)λ0>0是的一个特征值.

(ⅱ)x0>0，即x0的所有分量是正的.

(ⅲ)如果λ是的一个具有非负特征向量的特征值，则λ=λ0.此外，在不计倍数的情况下非负特征向量是唯一的.

(ⅳ)如果λ是的特征值，则|λ|≤λ0.

由定理2之(ⅱ)和(ⅳ)可知，非负张量的谱半径即是其最大特征值.

给定m阶n维非负张量=(ai1…im)，定义

ri()-ai…i，i∈〈n〉.

由文献[5]我们有

引理1设=(ai1…im)是m阶n维不可约非负张量，则ρ()>ai…i，i∈〈n〉.

文献[16]在非负张量上推广了关于非负矩阵谱半径上下界的Perron-Frobenius型定理：

定理3[16]假设=(ai1i2…im)是m阶n维非负张量，则

2 主要结果

在这一节中，我们给出一类非负张量谱半径的一个新的上下界估计结果.

定理4设=(ai1…im)是m阶n维弱不可约非负张量，满足aii2…im=0，当i∈{i2，…，im}{i:i=i2=…=im}时.记

.

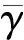
(1)

再由aii2…im=0，当i∈{i2，…，im}{i:i=i2=…=im}时，从而进一步有

(2)

由引理1知ρ()>ai…i，∀i∈〈n〉，从而由式(2)有

也即

从而ρ()≤xγ.因此ρ(

另一方面，由文献[17]存在一个简单环路γ′∈C(G)，不妨记γ′:j1→j2→…→jr→jr+1=j1，使得对都有xk≥xjl+1，l=1，2，…，r.类似上面的证明又有ρ()≥xγ′.因此ρ(证毕.

如果把定理4推广到一般的非负张量，可得如下结果：

定理5设=(ai1…im)是m阶n维非负张量，记

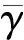
但在aii2…im≠0，存在i∈{i2，…，im}{i:i=i2=…=im}时，上面结果退化为定理3.因此，在定理4中假设aii2…im=0，当i∈{i2，…，im}{i:i=i2=…=im}是必要的.而文献[18]给出的引理2.1，实际上只有当aii2…im=0，当i∈{i2，…，im}时才是有意义的.

3 数值算例

例1设

计算知ρ()=5.211 1.应用定理3有4≤ρ()≤7，应用本文定理4有4.472 1≤ρ()≤5.916 1.因此，对于此类非负张量，估计其谱半径的上下界，本文定理4是一个很好的改进.