基于GS法球面4杆机构5精确点轨迹综合

魏锋， 魏世民， 张英， 李学刚

(1.北京邮电大学 自动化学院， 北京 100876；2.河南理工大学 机械与动力工程学院， 河南，焦作 454000)



基于GS法球面4杆机构5精确点轨迹综合

魏锋1，2， 魏世民1， 张英1， 李学刚1

(1.北京邮电大学 自动化学院， 北京 100876；2.河南理工大学 机械与动力工程学院， 河南，焦作 454000)

提出了球面4杆机构5精确点轨迹综合代数消元方法. 基于球面空间转移矩阵建立了该问题的设计方程，使用Groebner基和Sylvester结式(GS法)相结合的代数方法进行求解，最终获得一元高次方程及其全部封闭解析解. 通过数值实例，并使用Solidworks软件对计算结果进行仿真，结果表明该方法的正确性. 该方法为进一步采用代数法对其他类型球面机构轨迹综合问题的研究提供了参考.

轨迹综合；球面4杆机构；代数法；Groebner基；Sylvester结式

球面机构是一种介于平面机构与空间机构之间的特殊机构，球面上的所有转动副的轴线相交于球心，机构运动时其构件上的所有点与球心距离保持不变. 由于球面机构具有结构紧凑、灵活可靠、动力性能好等优点，在医疗、机械、宇航、电子等部门具有广阔的应用前景. 球面4杆机构是最基本的、最常用的球面机构. 目前，对球面4杆机构轨迹生成综合问题的研究主要分为轨迹曲线的近似综合[1-4]和轨迹点的精确综合[5-7]，其求解方法主要分为数值优化法和代数解析法. Hwang等[1]利用三角列线图法近似获取连杆曲线，讨论了7种形式的综合连杆曲线， 并建立了这些连杆曲线的隐式表达式，所陈述的三角列线图不仅可以用于构造所需的连杆曲线， 还可以用于机构轨迹综合优化设计. 孙建伟等[2]根据给出的球面4杆机构连杆轨迹的数学模型，借助傅里叶级数这一数学工具解决了球面4杆机构连杆轨迹综合问题. Penunuri 等[3]采用差分法对轨迹曲线近似综合. Angeles 等[4]采用最小平方法对轨迹曲线近似综合. Chiang[5]采用反转法，即通过固定曲柄反转机架获得兴趣点新位置，然后通过兴趣点原位置与新位置的连线中垂线相交求出曲柄上活动铰链点的位置坐标，以此解决球面4杆机构的3位置和4位置精确点轨迹综合问题，但该方法因预先设定曲柄转角，其应用受到限制. Tong等[6]采用极点法解决了有限精确点的轨迹综合，但其对轨迹方程的求解仍采用数值优化法. Suh等[7]采用位移矩阵法解决了4精确点轨迹综合问题，但是作者预先指定了连杆在4个不同位置的旋转角，其实质还是刚体导引综合问题.

综上所述，对球面4杆机构精确点轨迹综合研究，还只是定量地得到机构综合的数值解，尚未导出该问题的一元高次方程，无法对机构进行定性分析. 因此，运用代数解析法对球面4杆机构进行精确点轨迹综合研究具有一定的理论和实践意义. 本文使用分次逆字典序Groebner基与Sylvester结式相结合的代数方法，研究了球面4杆机构5精确点轨迹综合问题. 求解过程采用符号和有理数相结合的运算，可以对计算精度进行有效控制. 最后使用Solidworks软件对数据进行仿真，验证了结果的正确性.

1 球面刚体位移转移矩阵

球面4杆机构各杆间的运动副都是中心轴线通过球心的回转副(R副)，杆长可认为是球面上的弧长，由各杆所对球心角决定，由于取优弧和劣弧对机构没有影响，以下分析及计算中取任意杆的杆长小于180°. 球面铰链4杆机构的连杆位移可用连杆上沿着给定轨迹运动点的位移α1j和转角θ1j来表达. 如图1所示，α1j为点P的两个位置所决定的大圆绕uj轴的转角，而uj轴则垂直于大圆所在平面(该大圆中心即为球心co).θ1j为绕uo轴的转角.

P1(p1x，p1y，p1z)和Pj(pjx，pjy，pjz)为给定轨迹上点P的两个位置. 设r1=(P1-co)，rj=(Pj-co)，则它们所对的中心角α1j由下式决定为

(1)

在实际上运过程中算，为获得较高的运算精度，在推导过程中尽可能不取反三角函数运算，只有在结果中要获得角度值时，才用反三角函数. uj轴的方向由下式确定

(2)

考虑角位移θ1j，它是绕uo轴的转角，这里

(3)

于是可得球面刚体位移矩阵

(4)

式中Ruj，α1j和Ruo，θ1j可由刚体空间位移矩阵[7]获得

(5)

式中：versθ=1-cosθ，sθ=sinθ，cθ=cosθ.

2 建立精确点轨迹综合问题的设计方程

如图2所示为半径为R的球面4杆机构，建立以球心o为原点坐标轴任意的参考坐标系xoy，设A0(a0x，a0y，a0z)和B0(b0x，b0y，b0z)为固定铰链点，A1(a1x，a1y， a1z)和B1(b1x，b1y，b1z)为活动铰链点，4个铰链的转动轴线都相交于一点即球心o，P为固联于连杆A1B1球面上的一个兴趣点，机构在运动时其构件上的活动铰链点A1和B1以及点P相对与球心的距离均保持不变. 精确点轨迹综合就是求解各杆件的尺寸，并确保球面4杆机构在运动过程中点P精确的通过球面上给定的n个点Pj(pjx，pjy，pjz)(j=1，2，…，n).

(6)

(7)

根据点在球面上有

(8)

式(6)～(8)总共有2(n-1)+4个方程式，其中含有(n-1)+12个设计变量，即：A0，B0，A1，B1，θ1j(j=2，3，…，n). 根据方程式个数与变量个数必须相等的原则，可以得出给定精确点个数与任选参数的关系如表1所示.

表1 球面4杆机构精确点个数与任选参数的关系

Tab.1 Relationships between precision points of spherical four-bar linkage and parametric numbers

给定精确点数方程式个数机构变量数任选参数个数待求未知数个数261376381468410155105121641261417314716182168181911892020020

由表1可知轨迹综合的精确点个数最大为9，通常要综合的精确点个数越多，所涉及的非线性方程组结构越复杂，代数求解十分困难. 本文主要研究5精确点的轨迹综合代数法求解问题.

令cθj=cosθ1j，sθi=sinθ1j，并将式(4)及各坐标值代入式(6)，并展开得

(9)

(10)

(11)

式中ηj1，ηj2，ηj3，βj1，βj2，βj3见附录1.

式(8)～(11)共16个方程为球面4杆机构5精确点轨迹综合的设计方程，其中a0x，a0y，a0z，b0x，b0y，b0z，a1x，a1y，a1z，b1x，b1y，b1z和cθj，sθj(j=2，3，…，5)共20个变量为机构变量. 假设4个变量已知可求其他16个变量，本文假设固定铰链点a0x，a0y，b0x，b0y已知，其他16个待求变量为a0z，b0z，a1x，a1y，a1z，b1x，b1y，b1z，cθj，sθj(j=2，3，…，5).

3 消元与求解

为了不失公式的一般性，本文取R=1并令

(12)

则式(8)～(10)可变换为

(13)

(14)

(15)

3.1 求解分次逆字典序Groebner基

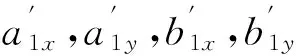
(16)

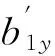
3.2 获取一元高次方程组

由代数学可知，方程组(16)有解的条件是其系数行列式等于0，即

(17)

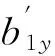
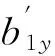
(18)

式中si为由输入参数确定的实系数.

由以上分析可知，本文构造的23阶单变量系数行列式与展开系数行列式后获得的一元多项式在符号形式上最高次数是完全一致的. 解式(18)，将得到36个复数解.

3.3 求解其他变量

4 数值算例

球面4杆机构的已知参数如下：

a0x=0.880 055，a0y=0.081 06，a0z=0.467 9，

b0x=-0.662 685，b0y=0.684 275，

b0z=-0.304 33，

p1x=0.939 693，p1y=0.342 019，p1z=0，

p2x=0.813 798，p2y=0.469 846，p2z=0.342 019，

p3x=0.620 886，p3y=0.166 366，

p3z=0.766 044，

p4x=0.683 013，p4y=-0.183 013，

p4z=0.707 106，

p1x=0.784 886，p1y=-0.365 998，

p1z=0.499 999.

根据上述步骤，可求得36组复数解，其中实数解为16组，如表2所示. 通过Solidworks软件仿真，可以验证表2中的数据满足通过5精确点的轨迹要求，例如序号1的仿真结果如图3所示.

序号A1(a1x,a1y,a1z)B1(b1x,b1y,b1z)1(0.8910,0.4478,0.0753)(-0.9514,0.3032,0.0547)2(0.7436,0.6677,0.0345)(0.1957,-0.1052,0.9750)3(0.8162,0.5768,0.0350)(-0.9908,0.0864,0.1040)4(0.8460,0.5307,0.0515)(-0.9830,0.0974,0.1554)5(0.4727,0.8773,0.0831)(0.9376,0.0646,0.3416)6(0.9512,0.3027,0.0605)(-0.5041,0.6366,0.5836)7(0.9080,0.4110,0.0810)(-0.8047,0.3703,0.4641)8(0.7775,0.5511,0.3031)(0.9426,0.0600,0.3286)9(0.8247,0.5502,0.1307)(0.7333,-0.2690,0.6244)10(0.9362,0.3385,0.0948)(-0.8614,0.4898,0.1342)11(0.9201,0.0221,0.3912)(0.9357,0.0731,0.3451)12(0.9193,-0.0354,0.3920)(0.9469,0.0587,0.3163)13(0.9217,0.0026,0.3880)(0.9219,0.0596,0.3829)14(0.8950,-0.1859,0.4056)(0.9376,0.0222,0.3470)15(0.9238,0.3701,0.0983)(-0.9936,0.0703,0.0886)16(0.9494,0.2863,0.1291)(-0.9939,0.0699,0.0849)

5 结 论

采用分次逆字典序Groebner基和Sylvester结式结合的代数方法求解球面4杆机构的5精确点轨迹综合问题，获得该问题其全部封闭形式的解析解. 求解过程中，不需要提取任何公因式，无增根且无漏根. 同时，使用Solidworks软件对数据进行验证，仿真证明了该方法的有效性. 文中提供的方法，适用于精确点数为5点及其以下的情况，对于5点以上的情况，由于非线性方程组结构复杂，目前尚未解决. 本文方法为进一步采用代数法对其他类型的球面连杆机构轨迹综合问题研究提供了参考.

[1] Hwang W M， Chen K H. Triangular nomograms for symmetrical spherical non-Grash of double-rockers generating symmetrical coupler curves[J]. Mechanism and Machine Theory， 2007，42(7):871-888.

[2] 孙建伟，褚金奎.用快速傅里叶变换进行球面四杆机构连杆轨迹综合[J].机械工程学报，2008，44(7):32-37.

Sun Jianwei， Chu Jinkui. Synthesis of coupler curves of spherical four-bar mechanism through fast Fourier transform[J]. Chinese Journal of Mechanical Engineering， 2008，44(7):32-37.(in Chinese)

[3] Penunuri F， Peón-Escalante R， Villanueva C， et al. Synthesis of spherical 4R mechanism for path generation using differential evolution[J]. Mechanism and Machine Theory， 2012，57:62-70.

[4] Angeles J， Liu Z. The constrained least-square optimization of spherical four-bar path generators[J]. Journal of Mechanical Design， 1992，114(3):394-405.

[5] Chiang C H. Synthesis of spherical four-bar path generators[J]. Mechanism and Machine Theory， 1986，21(2):135-143.

[6] Tong S H， Chiang C H. Syntheses of planar and spherical four-bar path generators by the pole method[J]. Mechanism and Machine Theory， 1992，27(2):143-155.

[7] Suh C H， Radcliffe C W. Synthesis of spherical linkages with use of the displacement matrix[J]. Journal of Manufacturing Science and Engineering， 1967，89(2):215-221.

[8] 廖启征.连杆机构运动学几何代数求解综述[J].北京邮电大学学报，2010，33(4):1-11.

Liao Qizheng. Geometry algebra method for solving the kinematics of linkage mechanisms[J]. Journal of Beijing University of Posts and Telecommunications， 2010，33(4):1-11.(in Chinese)

[9] 刘惠林，张同庄.3-RPR 平面并联机构正解的吴方法[J].北京理工大学学报，2000，20(5):565-569.

Liu Huilin， Zhang Tongzhuang. Forward solutions of the 3-RPR planar parallel mechanism with Wu’s method[J]. Journal of Beijing Institute of Technology, 2000，20(5):565-569.(in Chinese)

[10] Wolfram Research， Inc. Wolfram language & system documentation center[EB/OL]. [2014-07-29]. http://reference.wolfram.com/mathematica/ref/GroebnerBasis.html.

(责任编辑：李兵)

附录1

式中uj可由式(2)求得，α1j可由式(1)获得.

附录2

Five Precision Points Path Synthesis of Spherical Four-Bar Linkage Based on GS Method

WEI Feng1，2， WEI Shi-min1， ZHANG Ying1， LI Xue-gang1

(1.School of Automation， Beijing University of Post and Telecommunications， Beijing 100876， China;2.School of Mechanical and Power Engineering， He’nan Polytechnic University， Jiaozuo， He’nan 454000， China)

An algebraic elimination method for five precision points path synthesis of spherical four-bar linkage was presented. Firstly， the kinematic constraint equations of path synthesis were formulated based on the displacement matrix; And then， the equations were solved using Groebner-Sylvester (GS) hybrid approach， and a high degree univariate equation and its whole closed-form solutions were accordingly obtained. The results of numerical simulation with Solidworks validate the algorithm， and show that the proposed method can also be used to solve synthesis problems of other kinds of spherical linkages.

path synthesis; spherical four-bar linkage; algebraic method; Groebner basis; Sylvester resultant

2015-09-22

国家自然科学基金资助项目(51375059)；国家高新技术研究与发展计划资助项目(2011AA040203)；粮食公益性行业科研专项资助项目(201313009-06)；国家科技支撑计划课题资助项目(2013BAD17B06)；科学研究与研究生培养共建项目-科研项目资助项目(机器人应用关键技术研究)

魏锋(1977—)，男，博士生，副教授， E-mail:weif@bupt.edu.cn.

魏世民(1965—)，男，教授，博士生导师，E-mail:wsmly@bupt.edu.cn.

TH 112

A

1001-0645(2016)08-0789-06

10.15918/j.tbit1001-0645.2016.08.004