北斗系统星源伪距偏差特性分析及改正

朱少林，岳东杰，陈 健，汤同旭，章 媛

(河海大学地球科学与工程学院，江苏 南京 211100)

近年来一些研究表明[1-4]，北斗卫星伪距观测值中存在一类与卫星相关的系统误差，称为星源伪距偏差，其量级达到几分米到米。2012年，文献[5]发现北斗IGSO和MEO卫星存在伪距波动现象；2015年文献[6]对北斗伪距波动现象产生的原因进行分析，并建立了基于高度角变化的改正模型；2016年文献[7]进一步精细化了模型，一方面采用更长时段的观测数据进行拟合，另一方面提供了改正参数的精度信息，使其能够用于改进伪距观测量的随机模型；2017年文献[8]采用加权分段线性拟合联合抗差估计的方法建立了更精细的改正模型。

北斗IGSO和MEO卫星已建立了较为成熟的伪距偏差改正模型，但是GEO卫星由于在单个测站上卫星高度角变化微小，基于高度角的改正值也很微小，从而难以根据高度角变化建立伪距偏差改正模型。奇异谱分析(singular spectrum analysis,SSA)是一种从时间序列的动力重构出发且无需先验信息的无参数自适应分析方法，能较好地从含有噪声的有限尺度时间序列中提取趋势和周期等信息[9]，并且SSA与EMD、小波分析等滤波方法相比，去噪效果更优越且更稳定[10]。同时，在分析GEO卫星伪距多路径效应时，发现GEO卫星伪距偏差存在约为1 d的周期重复性。因此，本文针对GEO卫星伪距偏差问题，提出一种基于SSA的伪距偏差修正方法。首先采用SSA方法将前一天的伪距多路径去噪并提取出伪距偏差趋势项，然后将其作为下一天伪距观测值修正量的估计值，最后依据修正量修正下一天的伪距观测值。

1 北斗卫星伪距偏差

多路径组合观测值(multipath combination,MP)常用于分析伪距观测数据质量，其计算公式为

(1)

式中，p、φ分别表示伪距观测值和载波相位观测值；f、λ分别表示信号的频率和波长；下标i、j(i，j=1，2，3，i≠j)表示不同的信号频率；Bi表示载波相位模糊度、硬件延迟及多路径误差总和的常数部分；MPi表示第i个频率上伪距观测值的多路径误差值。

由式(1)可知，MP组合观测值消除了电离层误差和几何相关项，剩下包括相位观测值模糊度、信号硬件延迟、多路径误差和观测噪声的常数项。通过对一个卫星周期的多个历元的MP组合取平均作为B值，将原始MP组合减去B值后仅剩下伪距多路径和观测噪声。

图1分别给出了同一测站北斗GEO、IGSO、MEO和GPS卫星的MP时间序列和卫星高度角序列。可以看出，北斗3种卫星MP序列中均存在系统误差，即星源伪距偏差，而GPS卫星则不存在该类误差，表明该类误差与卫星相关。同时，IGSO和MEO卫星伪距偏差与高度角呈现负相关的关系，而GEO卫星由于高度角变化较小，没有表现出与高度角较强的相关性，但GEO卫星具有明显的伪距偏差，达到几分米甚至1 m，与IGSO和MEO卫星伪距偏差量级相当，在卫星定位中是不可忽略的一类误差。图1(a)中北斗GEO卫星两天伪距偏差具有相似性，笔者统计了连续10 d相邻两天MP序列的相关性，发现其相关系数均在0.68以上，因此GEO卫星伪距偏差呈现出一定的周期重复性，周期约为1 d。

2 GEO卫星伪距偏差修正方法

针对GEO卫星存在明显的伪距偏差且其具有周期约为1 d的重复性的特性，笔者首先采用SSA方法将前一天MP时间序列去噪后提取出伪距偏差项，然后用得到的伪距偏差项作为修正量来修正下一天的伪距观测值。下面主要介绍SSA方法的原理，以及分析修正伪距偏差后MP观测值的精度。

2.1 SSA数学模型

SSA[11]分析处理的对象是中心化后的一维时间序列{x1,x2,…,xN}，其实现过程主要分为以下5个步骤：

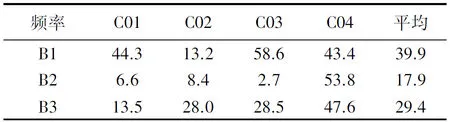
(1) 构建时滞矩阵。按给定嵌入空间维数M(M

(2)

(2) 时间经验正交函数分解。首先由时滞矩阵X计算滞后自协方差矩阵S=XXT(式(3))，然后求解矩阵S的特征值λ1≥λ2≥…≥λm≥0和对应的特征向量E1、E2、…、Em。特征值λk称为原序列{xi}的奇异谱，特征向量Ek称为时间EOF(T-EOF)，它反映了原序列{xi}的时间演变型。特征向量代表着信号的变化方向，最大特征值对应的特征向量代表了信号的最大变化方向，而较小特征值对应的特征向量一般视为噪声[12]。

(3)

(3) 计算时间主成分(T-PC)。原序列{xi}在Ek上的正交投影为

(4)

式中，ai,k是Ek所反映的时间演变型在原序列的xi+1,xi+2,…,xi+M时段的权重，称为时间主成分(T-PC)；0≤i≤N-M；1≤j≤M。

(4) 重建成分RC。第k个T-EOF和T-PC重建xi的成分RC，记为xi,k，公式[13-14]为

(5)

2.2 修正效果

用SSA方法分析CUT0测站2016年DOY32的观测数据，图2(a)为C01卫星B1频率上的MP原始序列和提取的趋势项，图2(b)为剔除趋势项后的MP序列。从图中可以看出，本文方法可以较好地剔除伪距偏差项，经过修正后的MP序列非常接近白噪声特性。

图3(a)给出了DOY32和DOY33相邻两天伪距偏差项对比，图3(b)为基于DOY32得到的修正量修正DOY33后的MP序列。需要说明的是，本文将文献[9]研究得出GEO卫星多路径周期约为86 160 s的结果作为修正周期。可以看出，图3(a)中相邻两天的修正量非常类似，且图3(b)中DOY33修正后的MP序列基本上消除了系统偏差，这进一步证实了可基于前一天数据获取的修正量对下一天的伪距观测值进行修正。图4为GEO各卫星未修正与基于前一天修正后的MP观测值精度对比，表1为各GEO卫星MP组合观测值精度提高百分比及各频率上精度提高百分比平均值统计，C05卫星由于观测质量很差，未进行改正。可以看出，修正后MP观测值精度有较明显的提高，在B1、B2、B3频率上分别平均提高了39.9%、17.9%、29.4%。

表1 MP组合观测值精度提高百分比 (%)

3 修正方法验证

本节主要通过MW组合观测值及BDS无电离层组合伪距单点定位来验证奇异谱分析方法修正GEO卫星伪距偏差的有效性。

3.1 MW组合序列分析

正常情况下，MW组合由于仅受测量噪声和多路径误差影响，其序列会在恒定值附近波动，若伪距观测值含有较大的系统误差，MW组合序列将发生系统性的偏移。因此，修正伪距偏差前后MW组合序列变化的情况可以用来验证修正的效果[15]。

图5为C02卫星伪距观测值修正前后MW序列的对比，图6为各GEO卫星伪距观测值修正前后MW精度的对比(DOY33，B1-B2)。从图中可以看出，修正后的MW序列基本上消除了系统误差，精度平均提高了41.3%，这验证了本文提出的SSA方法能很好地消除伪距偏差。

3.2 SPP定位结果分析

选取MGEX网CUT0测站2016年11 d(DOY31—DOY32)的观测数据，其中DOY31观测数据用于估计DOY32的伪距修正量。采用3种方案分别进行北斗B1和B2无电离层组合伪距单点定位，其中方案1：不进行伪距偏差改正；方案2：采用Wanninger和Beer模型修正IGSO和MEO卫星伪距偏差；方案3：采用Wanninger和Beer模型和本文提出的方法分别修正IGSO、MEO和GEO卫星伪距偏差。

图7为3种方案SPP坐标偏差时间序列，图8统计了10 d N、E、U方向上坐标偏差的标准偏差STD。结合图7和图8可以看出，采用Wanninger和Beer模型修正IGSO和MEO卫星伪距偏差对伪距单点定位结果影响不大，这可能是由于IGSO和MEO卫星伪距偏差较小，对定位精度低的伪距单点定位影响很小；而采用本文方法修正GEO卫星伪距偏差使伪距单点定位误差的标准偏差在平面上提高了11.1%，在高程方向上提高了21.1%。

本文对GEO卫星的修正需要用到前一天的双频载波相位观测值，采用后处理的方式，主要侧重于研究GEO卫星观测值伪距偏差对双频无电离层组合伪距单点定位的影响。当采用单频接收机进行实时定位时，本文方法并不适用。

4 结 语

本文对北斗系统存在的与卫星相关的星源伪距偏差进行了分析，并针对难以建立伪距偏差改正模型的GEO卫星提出了一种基于SSA方法的伪距偏差修正方法，利用前一天采用SSA方法得到的伪距修正量来改正下一天的伪距观测值。伪距偏差修正后，MP和MW组合观测值的精度都有所提高，基本上消除了GEO卫星伪距观测值中的系统偏差。并且，无电离层组合伪距单点定位试验结果表明，采用Wanninger和Beer高度角模型修正IGSO和MEO卫星伪距偏差对伪距单点定位精度影响很小，而采用SSA方法修正GEO卫星伪距偏差使伪距单点定位精度在平面和高程方向上分别提高了11.1%和21.1%。