两种伪距定位精度分析及计算程序的实现

李 韧，杨久东，龚栎澎，梁 鹏

两种伪距定位精度分析及计算程序的实现

李 韧，杨久东，龚栎澎，梁 鹏

（华北理工大学 矿业工程学院，河北 唐山 063210）

针对卡尔曼滤波伪距定位方法难以建立准确的定位模型，容易造成滤波发散，导致定位精度降低的问题，比较分析了卡尔曼滤波伪距定位和星频双差伪距定位两种伪距定位模型，利用三个点的静态观测数据，采用全球定位系统（GPS）的卫星伪距观测值和广播星历文件计算得到测站点坐标，将两种伪距定位模型计算的坐标与赫戈（HGO）软件静态解算的坐标进行精度对比与分析。结果显示，卡尔曼滤波伪距定位方法的误差在6 m内，星频双差伪距定位方法的误差在3 m内，对总体均方根误差（RMSE）进行分析，星频双差伪距定位结果低于卡尔曼滤波伪距定位，证明星频双差伪距定位精度高于卡尔曼滤波伪距定位精度，星频双差伪距定位数学模型是可行的。

伪距定位；卡尔曼滤波伪距定位；星间单差；星频双差；编程实现

0 引言

随着科技的发展，卫星导航定位为社会做出了重大贡献，伪距定位是其中不可或缺的一部分。它利用接收机的伪距观测数据及广播星历文件计算测站坐标，是导航定位中最常用的定位方法，主要用于导航定位中初始概略位置的定位[1]。随着对精密单点定位（precise point positioning, PPP）的研究深入，作为其基础方法及定位理论的伪距单点定位方法及理论也是极其重要的[2-3]。伪距定位已经不仅仅局限于传统的伪距定位，通过不断深入研究，已经衍生出多种伪距定位解算模型[4-5]。研究发现，采用最小二乘迭代法对伪距进行解算，其迭代次数少但定位精度较低[6-7]；采用卡尔曼（Kalman）滤波法解算，可使精度有所提高，但迭代次数过多[8]；很多学者研究使用最小二乘法和Kalman滤波法组合使用进行伪距解算，以减少迭代次数，提高定位精度[9]。伪距单点定位方法的精度一般为米级，组合伪距观测值定位精度可高于单一伪距观测值精度[10]，全球卫星导航系统（global navigation satellite system, GNSS）静态精密单点定位模型，点位精度可达毫米级[11-13]。

伪距单点定位方法及理论的研究虽然很多，但关于伪距定位的数学模型的表述却不够详细，笔者通过对伪距定位理论的进一步研究，整理出Kalman滤波伪距定位和星间频间伪距定位模型，以派森（Python）3.8为工具进行编程，并利用实测数据验证该数学模型的可行性、正确性及程序的稳定性，同时将两种伪距定位方法的定位结果进行比较，分析两种伪距定位方法的定位效果及精度，证明星频双差伪距定位精度高于卡尔曼滤波伪距定位精度，星频双差伪距定位数学模型是可行的。

1 伪距定位模型

1.1 Kalman滤波伪距定位模型

Kalman滤波方法是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法，在GNSS定位中应用较为广泛，适用于高精度卫星导航定位领域。首先建立Kalman滤波模型，即

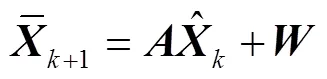
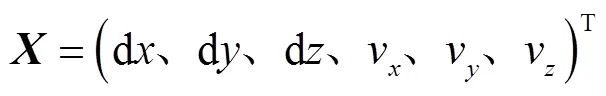
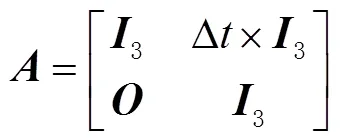
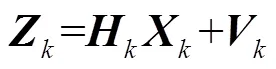
滤波器的递推公式为

通过Kalman滤波计算出测站的位置分量后，伪距定位坐标计算公式为

由于单独每个历元的数据都可解算一个测站点坐标，各历元数据可视作是独立观测值，可通过均方根误差（root mean square error, RMSE）指标，判别各历元解算坐标与平均值的变化幅度，坐标各分量的RMSE值和坐标的RMSE值的计算方法为

1.2 星间频间伪距定位模型

根据伪距定位原理，可将伪距公式进行变形整理后得

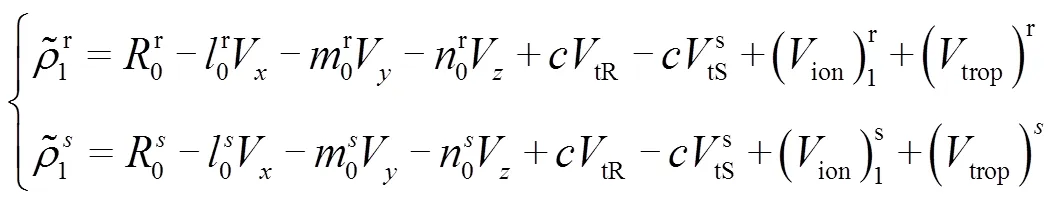
参考卫星的观测方程与其余卫星的观测方程进行星间作差，可得

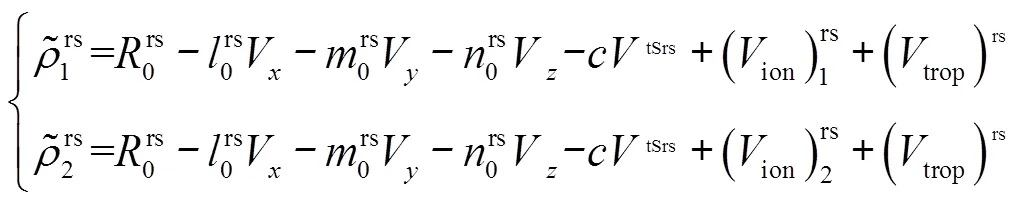
GPS卫星信号播发频率L1是由调制基本频率154×10.23 MHz获得的频率，L2是由调制基本频率120×10.23 MHz获得的频率，所以有

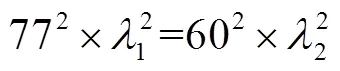
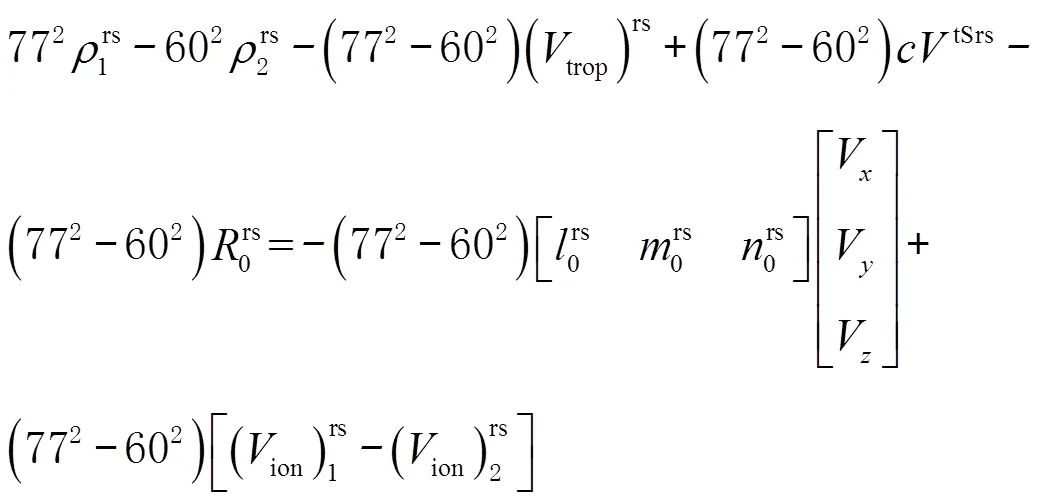
因为星间频间伪距定位方法是依据L1、L2频率间倍率关系作差进行计算定位的，但卫星的频率发射不稳定，存在一定的频率波动，在后期解算中，需要对系数进行一系列调整，才能利用最小二乘计算出较为精确的测站的伪距定位坐标。最小二乘解算中的权阵采用同一历元下卫星高度角定权模型，权阵为方差阵的逆，其方差计算方法为

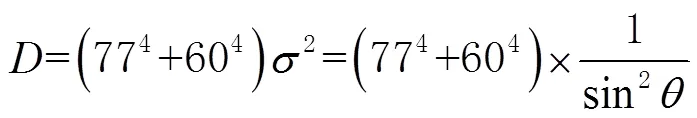
观测误差方程为

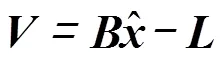
由最小二乘求解得

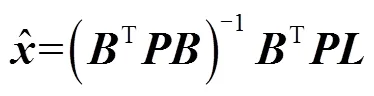
由式（17）可以求得坐标改正值，将坐标改正值代入式（18）可以求得接收机坐标为

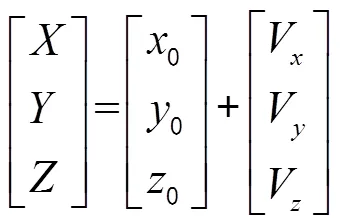
2 定位坐标解算及精度分析

在利用Python语言进行两种伪距定位模型的程序设计时，建立了不同的模块来实现伪距定位坐标的计算，主要包括文件读取、坐标转换、时间统一、卫星位置计算、伪距定位模型计算、精度评价等6大模块，定位程序主要处理流程如图1所示。

图1 程序设计流程图

在计算伪距定位时，需要注意坐标系转换。由于GPS定位求得的各种参数为1984世界大地坐标系（world geodetic coordinate system 1984, WGS84）下的结果，在测站坐标计算的过程中，需要根据实际测绘工作需要，将WGS84坐标转换为站心坐标系。

运用本文所述的两种伪距定位模型，选择2019年11月河北省唐山市曹妃甸生态城控制网中C401、C410和GPS1三个控制点的静态观测数据进行试验，C401与C410的距离为5493 m，C401与GPS1的距离为1950 m，C410与GPS1距离为4348 m。同步观测时间为100 min，静态接收机型号为海星达IRTK2型双频接收机，静态数据文件为RINEX3.02文件，采样间隔1 s，高度截止角为10°，因观测时间较长，故选取观测历元中的300个历元参与模型计算。程序自动计算1~300个历元、两个伪距定位模型中的定位坐标，同时使用中海达赫戈（HGO）基线解算软件进行控制网解算，经严密二维约束平差后，最弱点中误差的最大值为1.19 mm，符合精度要求。由于相对伪距定位模型的精度为米级，可以将HGO解算的二维约束平差结果作为真值使用。图2至图10为对两种伪距定位模型进行比较的结果。

图2至图4为测站C401的坐标值（、、），图5至图7为测站C410的坐标值（、、），图8至图10为测站GPS1的坐标值（、、）。从图2至图10可知，三个测站的Kalman滤波伪距定位模型和星间频间伪距定位模型的每个历元解算的定位坐标，都出现了不同程度的波动，符合伪距定位的解算规律。在两种定位方法模型解算的300个历元坐标中：Kalman滤波伪距定位方法在前10个历元处波动较大，原因在于，在动态滤波过程中，Kalman滤波需要一定的历元数进行收敛，而收敛后的图线波动较小，图形表现较为平稳；星间频间伪距定位模型解算的300历元定位坐标，波动较大，大部分图线波动在精密坐标图线的上方与下方，其平均值与精密坐标图线更为接近。

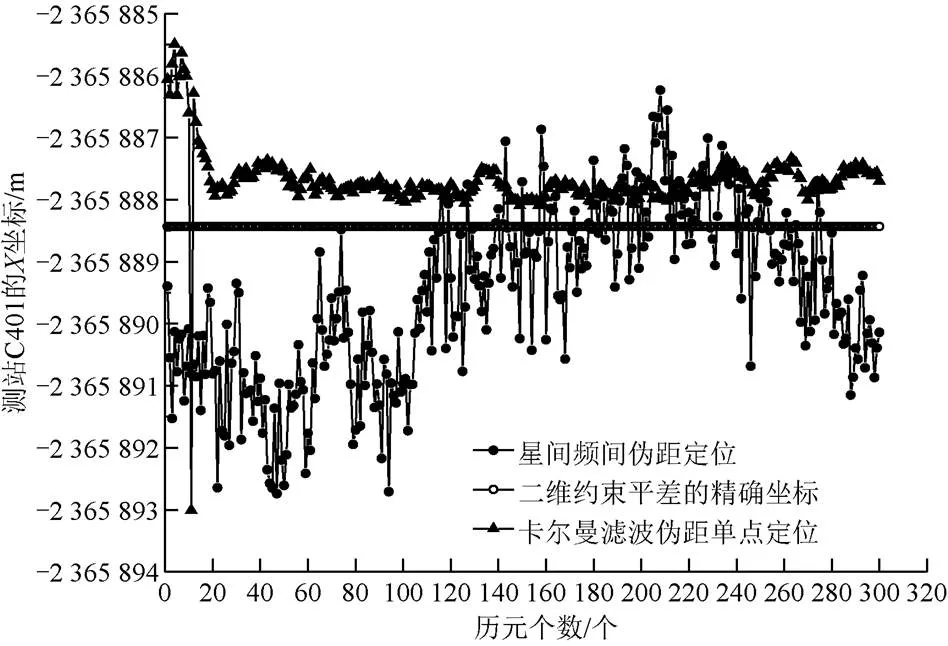
图2 测站C401的X坐标值

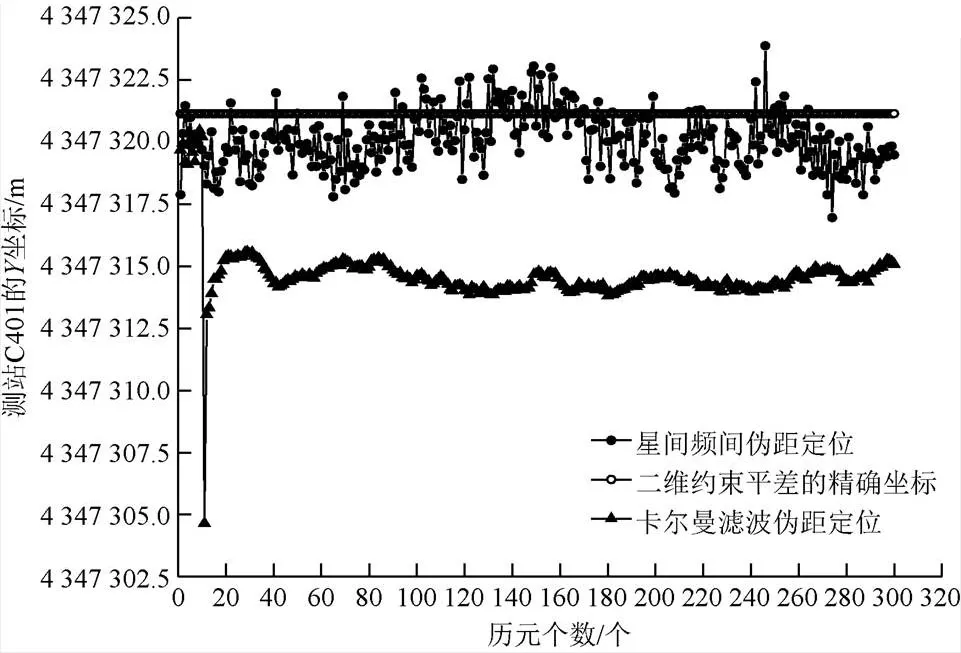
图3 测站C401的Y坐标值

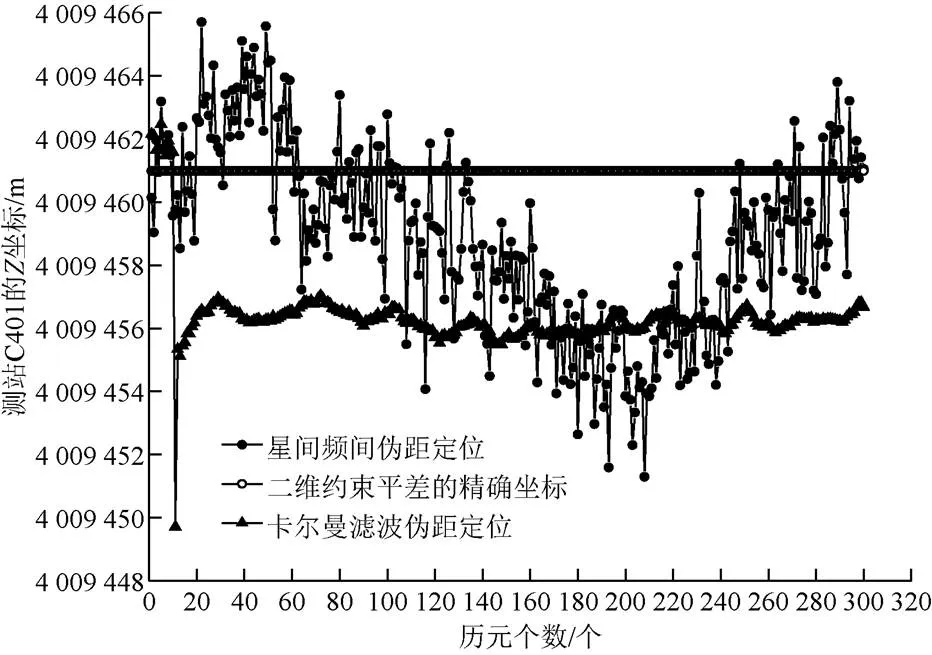
图4 测站C401的Z坐标值

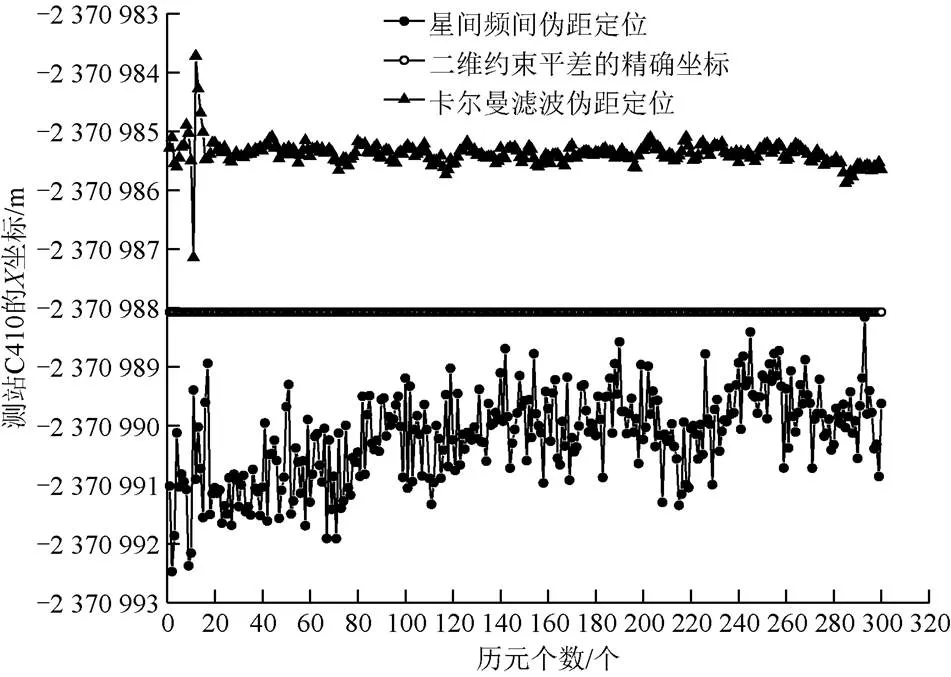
图5 测站C410的X坐标值

图6 测站C410的Y坐标值

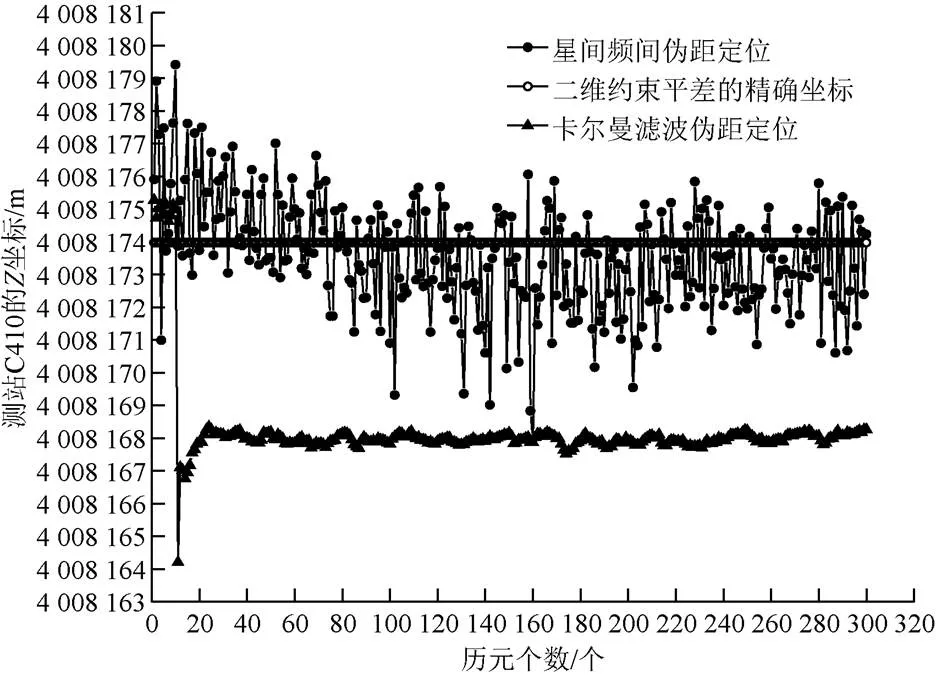
图7 测站C410的Z坐标值

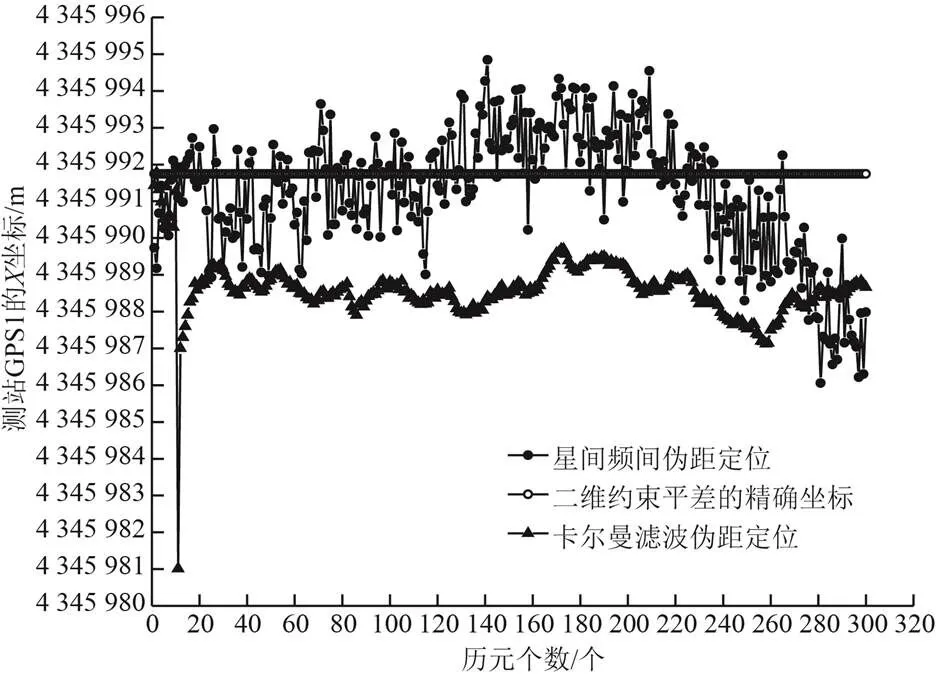
图8 测站GPS1的X坐标值

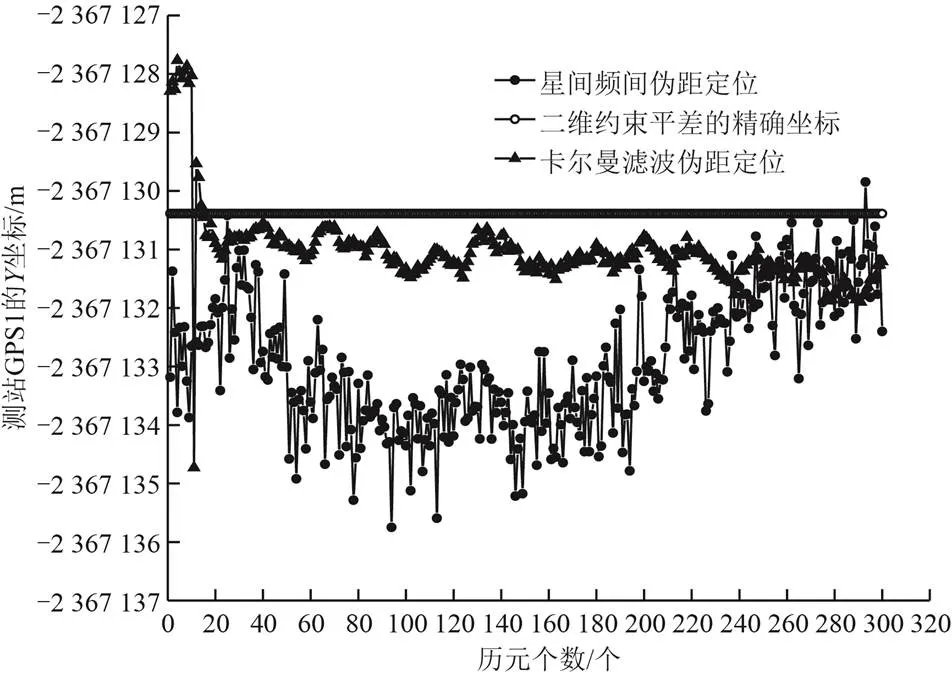
图9 测站GPS1的Y坐标值

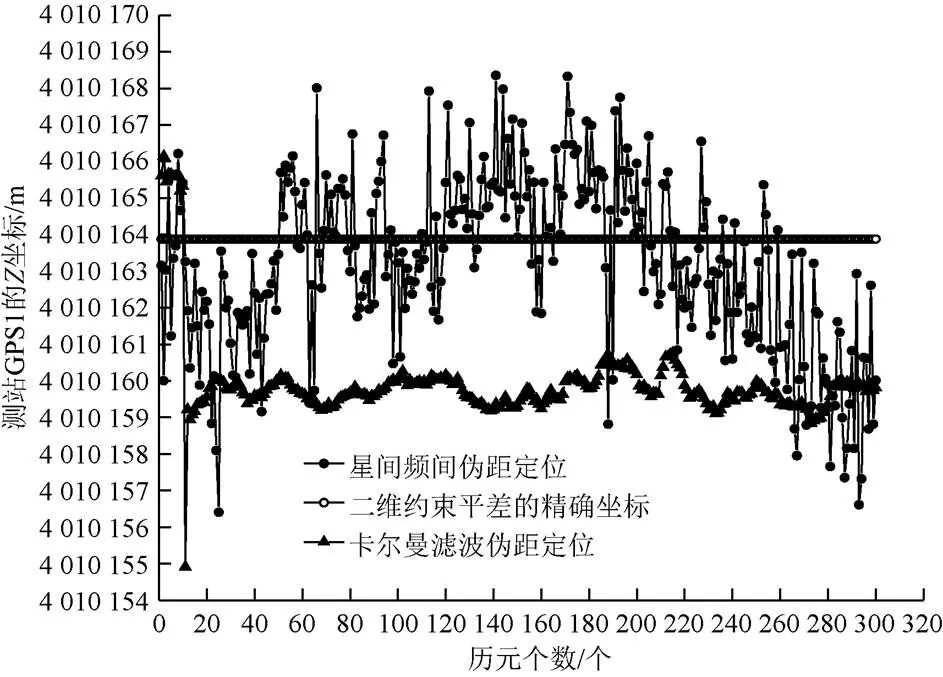
图10 测站GPS1的Z坐标值

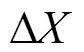
表1 测站定位坐标误差及坐标变化范围

为了更直观地反映观测值偏离真实有效数据值的波动情况，将其结果列于表2，RMSE值越小，表明误差就越小，精度越高，伪距定位越准确。通过对表2进行分析可知，用两种伪距定位方法在三个测站进行300个历元的解算，三个测站的RMSE值表现一致，均是卡尔曼滤波伪距定位的坐标解算精度高于星间频间伪距定位，而星间频间伪距定位在三个测站上的RMSE、RMSE、RMSE的值均低于卡尔曼滤波伪距定位，其中测站C401、测站C410和测站GPS1的星间频间伪距定位的总体均方根误差RMSE比Kalman滤波伪距定位分别提升了48%、68%和24%。综合分析，星间频间伪距定位方法的定位精度要高于Kalman滤波伪距定位，但是坐标解算精度低于Kalman滤波伪距定位精度，主要原因可能在于选择的解算模型不够精确，在定位计算中发生了偏移，导致定位精度不高。

表2 测站RMSE值

3 结束语

本文对两种伪距定位的数学模型进行分析和研究，用Python程序实现了Kalman滤波伪距定位模型、星间频间伪距定位模型的计算，并利用静态实测数据进行分析，测站点的伪距定位精度在米级，Kalman滤波伪距定位方法计算的、、坐标误差在6 m内，星间频间伪距定位方法计算的、、坐标误差在3 m内，星间频间伪距定位的精度高于Kalman滤波伪距定位。在经过大量实测数据的计算检验后，表明笔者编制的伪距定位程序可以满足要求。由于实验数据区域较小，属于短基线解算，对流层及电离层误差影响较小，而且仅仅采用GPS单系统的伪距观测值进行了伪距计算，未加入其它卫星系统的数据进行联合解算。若在后期能加入其它卫星系统的数据进行有效组合伪距定位，则能进一步提高伪距定位精度及稳定性。

[1]卫柳艳. GPS网络RTK系统的算法及定位精度研究[D]. 南京: 河海大学, 2006: 2-6.

[2]CAI Changsheng, GAO Yang. Modeling and assessment of combined GPS/GLONASS precise point positioning[J]. GPS Solutions. 2013, 17(3): 223-236.

[3]CAI C S, KUANG C L, DAI W J. Performance analysis of combined GPS/GLONASS precise point positioning[J]. Science of Surveying & Mapping, 2012, 37(3): 183-185.

[4]原洪峰, 杨龙, 蒋德. 不同实验条件下GPS伪距定位精度分析[J]. 全球定位系统, 2005, 17(5): 23-26.

[5]DING He, SUN Fuping, LI Yaping, et al. Modeling and performance analysis of combined BDS/GPS/GLONASS precise point positioning[J]. Journal of Geodesy & Geodynamics, 2016, 36(4): 303-307.

[6]王祖荫. 卡尔曼滤波与经典最小二乘法[J]. 岩矿测试, 1993, 12(1): 23-26.

[7]LI P, ZHANG X H. Modeling and performance analysis of GPS/GLONASS/BDS precise point positioning[C]//China Satellite Navigation Conference (CSNC). Proceedings of Lecture Notes in Electrical Engineerin: Volume III. Berlin, Heidelberg: Springer, 2014: 251-26. DOI: https: //doi. org/10.1007/978-3-642-54740-9_23[2020-05-18].

[8]王小冬. 卡尔曼滤波在卫星导航中的应用研究[D]. 大连: 大连海事大学, 2008: 5-9.

[9] 刘春, 马颖. 改进卡尔曼滤波在北斗伪距定位中的研究[J]. 电子测量与仪器学报, 2016, 23(5): 779-785.

[10] 李旺, 乔灵娜. 约束条件下GPS伪距定位精度分析[J]. 测绘与空间地理信息, 2019, 42(4): 76-78

[11] 王趁香. GPS/BDS精密单点定位算法研究与实现[D]. 阜新: 辽宁工程技术大学, 2017: 5-9

[12] 崔立鲁, 杜石, 余寒, 等. BDS/GPS组合伪距单点定位性能分析与评价[J]. 测绘工程, 2019, 28(2): 17-20, 25.

[13] 杨徐, 徐爱功, 秦小茜, 等. 高度角定权模型的BDS/GPS伪距单点定位分析[J]. 导航定位学报, 2017, 5(2): 72-78, 85.

[14] 李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009: 65-68.

[15] 符华年, 张旭东, 胡玉坤. GPS静态精密单点定位算法精度分析[J]. 测绘通报, 2019(2): 95-98. DOI: 10. 13474 /j. cnki. 11-2246. 2019. 0051.

[16] 郭平, 周适, 段太生, 等. 一种伪距单点定位的数学模型研究及程序实现[J]. 全球定位系统, 2019, 44(4): 53-60.

Accuracy analysis and program implementation of two kinds of pseudo range positioning

LI Ren,YANG Jiudong,GONG Lipeng,LIANG Peng

( Mining Engineering College,North China University of Technology,Tangshan,Hebei 063210,China)

The Kalman filter pseudo-range positioning method finds it difficult to establish an exact positioning model and filtering divergence could be easily caused which reduce the accuracy of position. In point of these problems, we have compared and analyzed two pseudo-range positioning model,namely Kalman filter pseudo-range positioning model and star frequency double difference pseudo-distance positioning, taken advantage of static observation data measured by engineering at 3 points, gotten the satellite pseudo-distance measured data of the Global Positioning System (GPS) and measured position coordinates computed by broadcast ephemeris.Comparing and analyzing the accuracy of coordinates computed by the pseudo-distance positioning model and by the static HGO software, we can find that the error range of Kalman filter pseudo-range positioning model is within 6 m and the star frequency double difference pseudo-distance positioning is within 3 m. Analyzing the value of General Root Mean Square Error (RMSE), we can see that the positioning results of star frequency double difference pseudo-distance are all lower than the Kalman filter pseudodistance positioning. It has demonstrated that the accuracy of star frequency double difference pseudo-distance positioning is higher than the Kalman filter pseudo-distance positioning and its feasibility for star frequency double difference pseudo-distance positioning to locate math models.

pseudo range positioning;Kalman filter pseudo range positioning;single difference between stars;double difference between stars;programming implementation

P228

A

2095-4999(2021)02-0083-07

李韧，杨久东，龚栎澎，等. 两种伪距定位精度分析及计算程序的实现[J]. 导航定位学报, 2021, 9(2): 83-89.（LI Ren, YANG Jiudong, GONG Lipeng, et al. Accuracy analysis and program implementation of two kinds of pseudo range positioning[J]. Journal of Navigation and Positioning, 2021, 9(2): 83-89.）

10.16547/j.cnki.10-1096.20210213.

2020-06-17

国家自然科学基金项目（51904105）。

李韧（1996—），男，河北廊坊人，硕士研究生，研究方向为空间大地测量。

龚栎澎（1995—），男，河北唐山人，硕士研究生，研究方向为空间大地测量。