合理构造 巧妙化归

江苏省南京市金陵中学　　　(210005)

于　健

江苏省南京市第二十九中学　(210036)

郭建华



合理构造巧妙化归

江苏省南京市金陵中学(210005)

于健

江苏省南京市第二十九中学(210036)

郭建华

构造法是数学解题中很重要的一种化归手段，在解题中被广泛应用．所谓构造法，就是根据题设条件和结论的特殊性，构造出一些新的数学形式，并借助它认识与解决原问题的一种思想方法．应用好构造思想解题的关键有二：一是要有明确的方向，即为什么目的而构造；二是弄清条件的本质特点和背景，以便重新进行逻辑组合．构造的方法有很多，常见的有构造表达式、构造图形、构造模型等，下面笔者结合一些实例归类分析，谈谈构造法在数学解题中的运用．

1　构造表达式

数学知识形式化的特点决定了适当的转化、构造表达形式可以起到融合知识，开阔思路，化未知为已知，从而达到解决问题的目的．常见的构造表达式有构造函数、构造方程、构造向量、构造恒等式等几种.

1.1构造函数

结合已知条件，适当构造函数，转化矛盾，利用函数的图像和性质解决问题，将会给我们的解题带来很大的方便.

例1设a+lga=10，b+10b=10，求a+b的值.

分析：直接解方程无从下手，观察两个方程的结构，若设f(x)=x+lgx，则f(a)=a+lga，f(10b)=10b+lg10b=10b+b．

解：设f(x)=x+lgx，则f(a)=10=b+10b=lg10b+10b=f(10b)，由于f(x)在(0,+)上是单调递增函数，所以a=10b，故a+b=10b+b=10.

1.2构造方程

方程是解数学题的一个重要工具,许多数学问题,根据其数量关系,在已知和未知之间搭上桥梁,构造出方程,使解答简洁、合理.

例2设a>b>c,a+b+c=1,a2+b2+c2=1,求a+b的取值范围.

分析：已知中三个变量,两个关系式,移项变形可用c表达a,b的关系,观察规律,可以想到构造以a,b为两根的方程.

(1)2-(2)得ab=c2-c(3)，

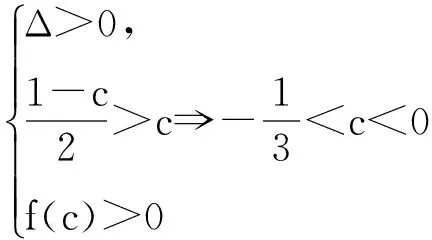
由(1)、(3)两式说明:a,b是关于x的一元二次方程x2-(1-c)x+c2-c=0(4)的两个不相等的实根,且因为已知a>b>c,表明方程(4)的两根都大于c.

1.3构造向量

新教材的一个重要特点就是引入向量，使得代数、几何、三角中的很多问题都可以利用向量这一重要工具来解决.

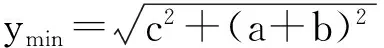
1.4构造恒等式

有些问题借助于构造恒等式采取赋值的方法可以轻巧的达到求解目的.

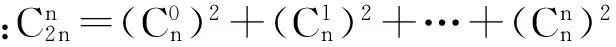
分析:根据组合数的特点,可以想到构造二项式,根据二项展开式的系数证明.

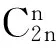
2　构造图形

所谓构造图形，就是以已知为前提，构造一些理想的图形，其目的是通过这个图形直观地揭示已知与未知的关系，确定论证出发点，使证题的思路豁然开朗，体现了数形结合的思想.

2.1构造平面图形

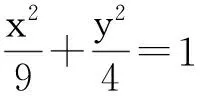
分析：由平面几何知识,要使∠F1PF2为钝角,当且仅当点P在以F1F2为直径的圆的内部,为此可以想到构造以F1F2为直径的圆面x2+y2<5.

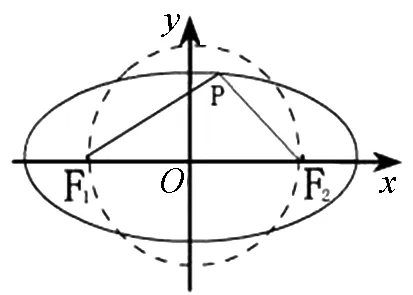
图1

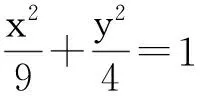
2.2构造空间几何体

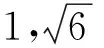
分析：由题意一个三棱锥S﹣ABC的三条侧棱SA、SB、SC两两互相垂直，可知，三棱锥是长方体的一个角，扩展为长方体，两者的外接球相同，长方体的对角线就是球的直径，求出直径即可求出球的表面积．

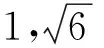
3　构造模型

数学和其他学科一样,要学以致用,“建模”思想就是把数学这门高度抽象的基础学科与实际生活紧密联系起来,在实际中渗透数学思想,把数学中的理论作为工具,充分发挥其作用,因而许多问题可通过构造模型来处理.近年来,构造模型的方法越来越被重视,并成为高考和数学竞赛中一道独特的风景线.

例6要从高三年级6个班中选出10人组成“蓝球队”,每班至少要选一人参加,则名额分配方案有种.

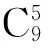
由上述各例分析可见，构造法是一种极富技巧性和创造性的解题方法，体现了数学中发现类比化归的思想，也渗透着猜想探索特殊化等重要的数学方法．运用构造法解数学题可从中欣赏数学之美，享受解题乐趣，更重要的是可开拓思维空间，启迪智慧，并对培养多元化思维创新精神大有裨益．

*江苏省教育科学“十二五”规划立项课题：信息技术环境下高中数学“问题—探究—解决”教学模式的应用研究(D/2013/02/445)的研究成果之一.