基于模糊逻辑的导弹扩展比例导引律

邵 节，刘佳琪，张 超，刘 芳，彭程远



基于模糊逻辑的导弹扩展比例导引律

邵 节，刘佳琪，张 超，刘 芳，彭程远

（北京航天长征飞行器研究所，北京，100076）

临近空间高超声速大机动目标的拦截制导律一直是现代制导与控制方面的一个难点和热点。运用模糊逻辑的方法，改进了扩展比例导引律，使导弹在拦截过程中能够有效跟踪导弹至目标视线转率的变化及目标的机动加速度，拦截末段视线转率收敛，实施成功拦截。

模糊逻辑；扩展比例导引；制导；导弹；拦截

0 引 言

在导弹拦截目标的二体相对运动过程中，导引律起着极其重要的作用，成为导弹能否对目标进行成功拦截的关键因素。传统的比例导引律已经被证明能够对非机动的目标进行成功拦截。扩展比例导引律在传统比例导引律的基础上，引入了目标的加速度项，使导弹能够针对目标的机动产生合理的控制指令，控制导弹对目标进行拦截[1]。但是，在扩展比例导引律中，导弹需用过载往往要比目标的机动过载大3倍。因而，对临近空间高超声速大机动目标进行拦截，还需要更为合适的导引律。

模糊逻辑作为一门新兴的控制理论，建立在多值逻辑的基础上，借助于隶属度函数概念，运用模糊集合的方法研究模糊性思维、语言形式及其规律[2]，在航空航天制导与控制领域发挥越来越重要的作用。

1 导弹的扩展比例导引律

传统的比例导引律是在假设导弹飞行期间导弹速度和目标速度恒为常值的基础上推导出来的[3]，如图1所示。

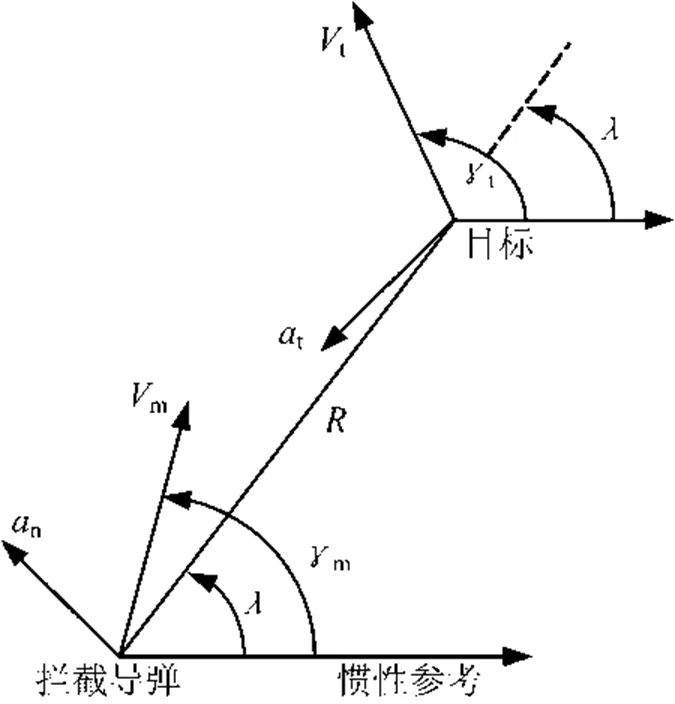
图1 比例导引的几何关系

n—拦截导弹的加速度；t—目标的机动加速度；—导弹与目标间的距离；—拦截导弹的速度；—目标的速度；—视线角；—导弹航迹角（或航向角），也就是导弹速度矢量和惯性参考之间的夹角；—目标航迹角

由图1所示的几何关系可得，视线角在任意时刻的转动速率由目标与导弹的速度法向分量的差值除以距离给出。即：

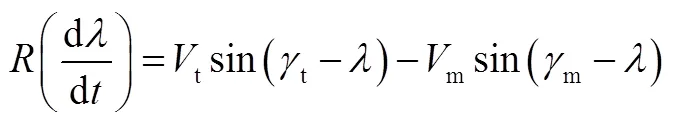
而沿视线的速度分量由以下方程给出，即：

（2）

经典的比例导引方程为

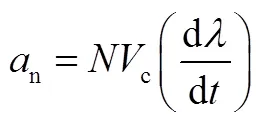
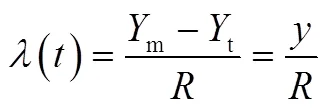
拦截时间可表示为

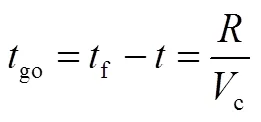
将式（5）代入式（4）中，得：

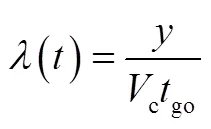
对式（6）求导，可得：

（7）

将式（7）代入式（3）可得：

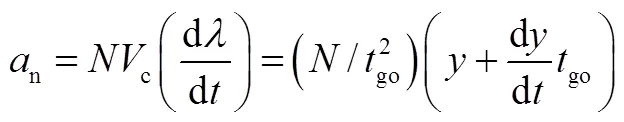
（9）

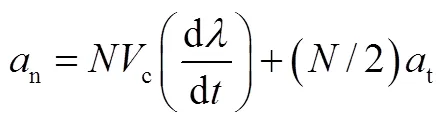
式（10）表示扩展比例导引制导律。

2 导弹制导的模糊逻辑控制

导弹制导的模糊逻辑控制采用状态估计模糊控制法。输入状态为导弹与目标的相对速度c、视线转率及目标的机动加速度，输出指令为拦截导弹的加速度。其控制过程如图2所示。

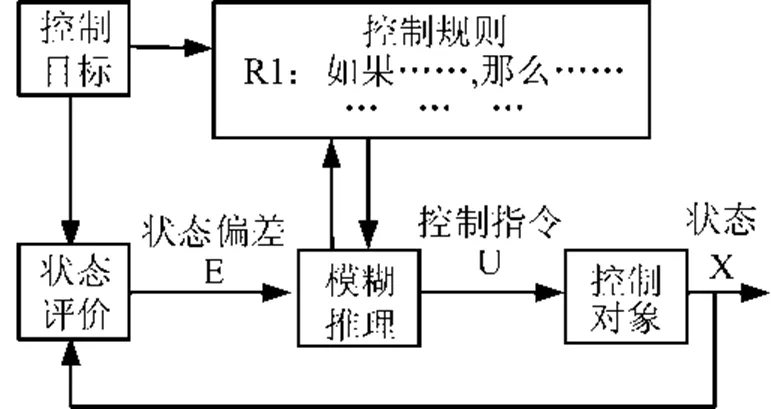
图2 简单状态估计模糊控制方法

状态估计模糊控制器的设计过程一般分为3个步骤：模糊状态的模糊定量；模糊控制规则；模糊控制规则和状态的调整。

a）模糊状态的模糊定量。

对模糊输入、输出状态（相对速度c、视线转率及导航常数）应用模糊集合的隶属函数进行定义，即模糊定量。由于末制导过程中相对速度c和导航常数始终为正，模糊词集为PB（正大）、PM（正中）、PS（正小），隶属函数曲线见图4。视线转率正负均有值，模糊词集为PB（正大）、PM（正中）、PS（正小）、ZE（零）、NS（负小）、NM（负中）、NB（负大），隶属函数曲线分别见图3。

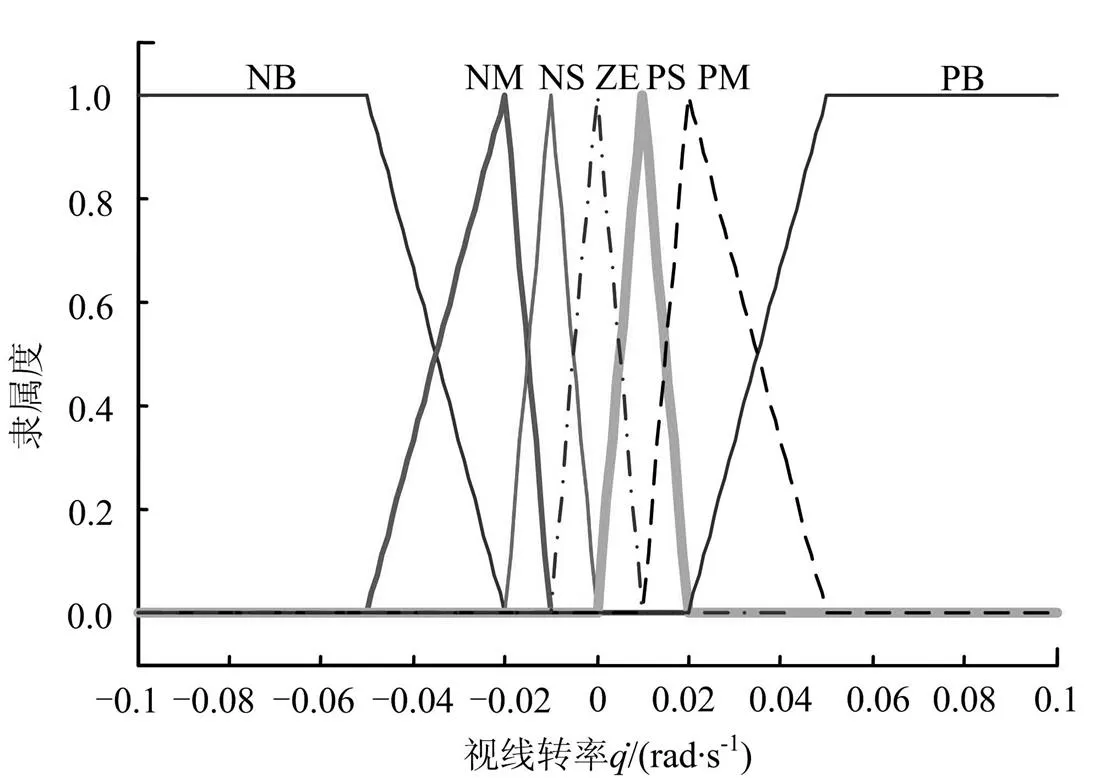
图3 的隶属度函数

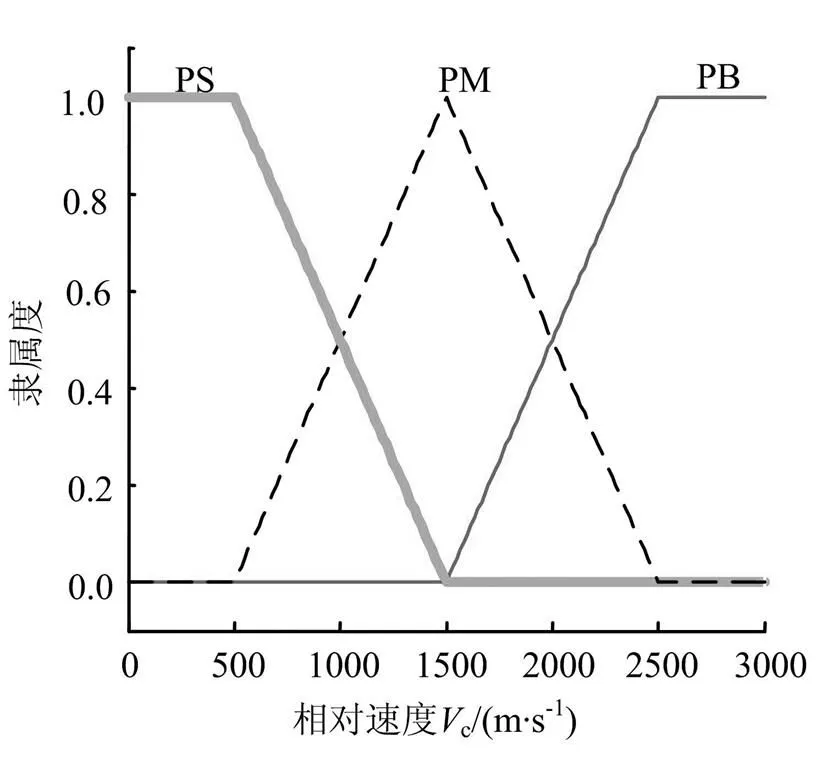
a）相对速度

b）导航常数

图4c和的隶属度函数

b）模糊控制规则。

对导弹拦截目标的过程进行规格化，设法用If-then形式将它们写成所采用的计算机语言能表达的符号化的模糊控制规则[5]，例如If Vc=PB and=PB then N=PB，其模糊规则库如表1所示。

表1 模糊制导律规则库

根据系统的实际情况，经过拦截仿真试验对原有模糊控制规则的推理可能会相互产生影响甚至还会产生矛盾，这就需要对原有规则以及分档的模糊状态（即模糊集合的隶属函数）进行修改、调整、合并、删除和补充[6]。

3 仿真结果

本文对比例导引律和模糊制导律在4种目标机动条件下的导弹拦截过程进行仿真分析，比较其导引品质。拦截相对运动几何关系，见图5。

图5 攻击平面图

—拦截弹到目标的视线角；—目标与拦截弹的相对距离；—拦截弹的指令加速度；—目标的机动加速度；拦截弹的最大机动能力为20

仿真初始条件为：

a）案例1：目标做常值机动，机动加速度大小为100 m/s2。仿真结果见图6和图7。

由拦截弹与目标的二维交战图可以看出，当目标做常值机动，机动加速度大小为100 m/s2时，比例导引律和模糊制导律均能导引拦截弹成功拦截目标。由拦截弹与目标的视线转率及过载变化曲线可以看出，比例导引律的视线转率发散更快。模糊制导律能够有效跟踪目标的机动加速度，产生相应的制导控制指令，抑制拦截弹视线转率发散，从而降低拦截脱靶量。

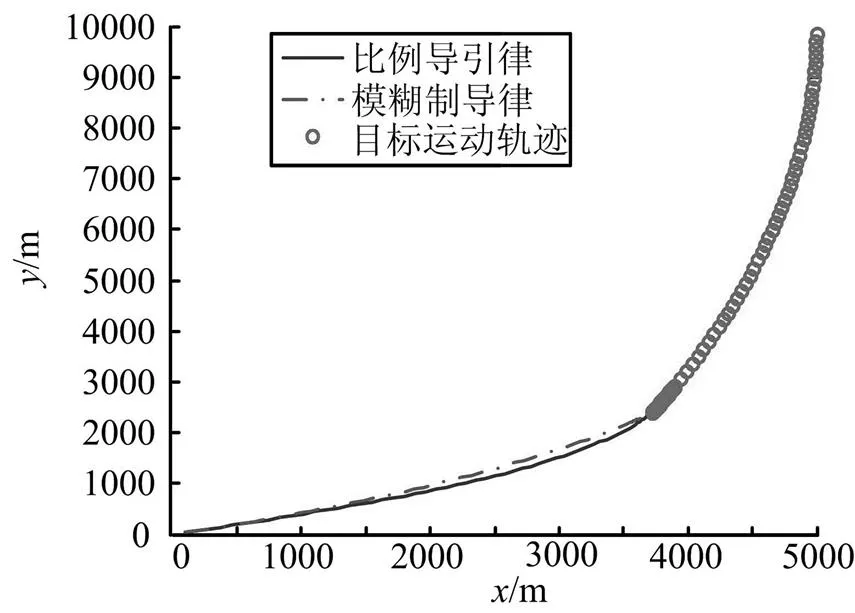
图6 案例1拦截弹与目标二维交战图

a）视线转率变化

b）过载变化

图7 案例1拦截弹与目标的视线转率及过载变化曲线

b）案例2：目标做变加速度机动，加速度大小递减，变化范围为200~100 m/s2。仿真结果见图8和图9。

由拦截弹与目标的二维交战图看出，当目标做变加速度机动，加速度大小递减，变化范围为200~100 m/s2时，比例导引律未能成功拦截目标，脱靶量较大，为274.404 6 m；而模糊制导律能够成功拦截目标，脱靶量为1.556 7 m（根据目标尺寸大小，认为拦截脱靶量小于3 m时拦截成功）。由拦截弹与目标的视线转率及过载变化曲线可以看出，由于比例导引律的需用过载大于拦截弹的最大机动能力20，使得视线转率很快发散，无法成功拦截目标。模糊制导律能够有效跟踪目标的机动加速度，产生相应的制导控制指令，抑制拦截弹视线转率发散，从而降低拦截脱靶量。

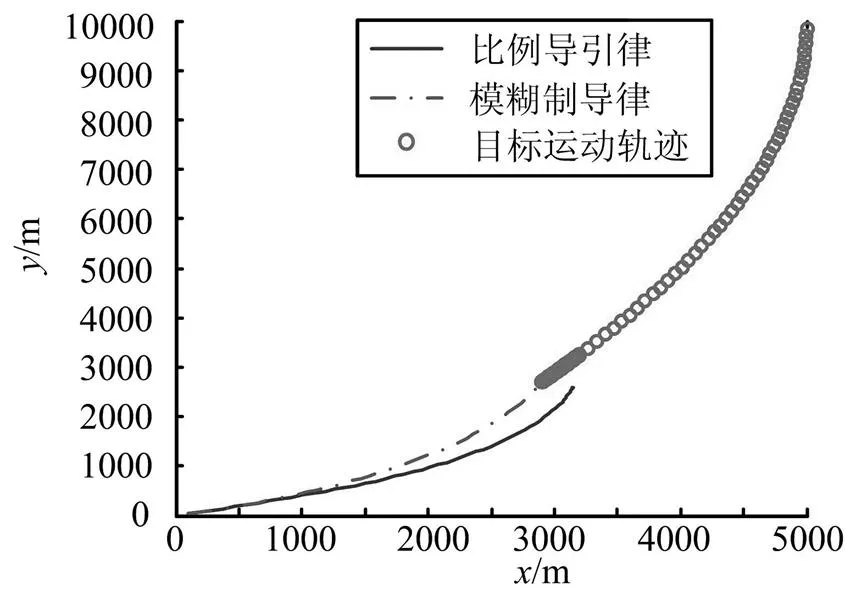
图8 案例 2拦截弹与目标二维交战图

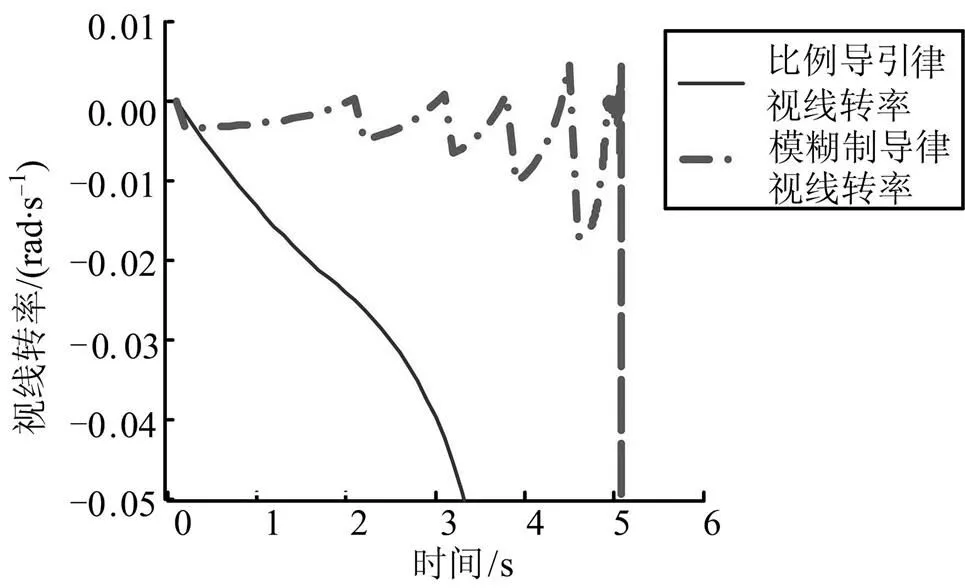
a）视线转率

b）过载变化

图9 案例2拦截弹与目标的视线转率及过载变化曲线

c）案例2：目标做变加速度机动，加速度大小递增，变化范围为100~200 m/s2。仿真结果见图10和图11。

由拦截弹与目标的二维交战图可以看出，当目标做变加速度机动，加速度大小递增，变化范围为100~200 m/s2时，比例导引律未能成功拦截目标，脱靶量较大，为234.079 0 m；模糊制导律也未能成功拦截目标，脱靶量为31.030 7 m。与案例2相比，由于目标的机动加速度是递增的，随着拦截弹与目标的距离越来越近，目标的机动加速度越来越大，使得拦截弹与目标的视线转率变化更加剧烈，超出了制导律的跟踪修正能力，视线转率较早就发散了，因而脱靶量较大。

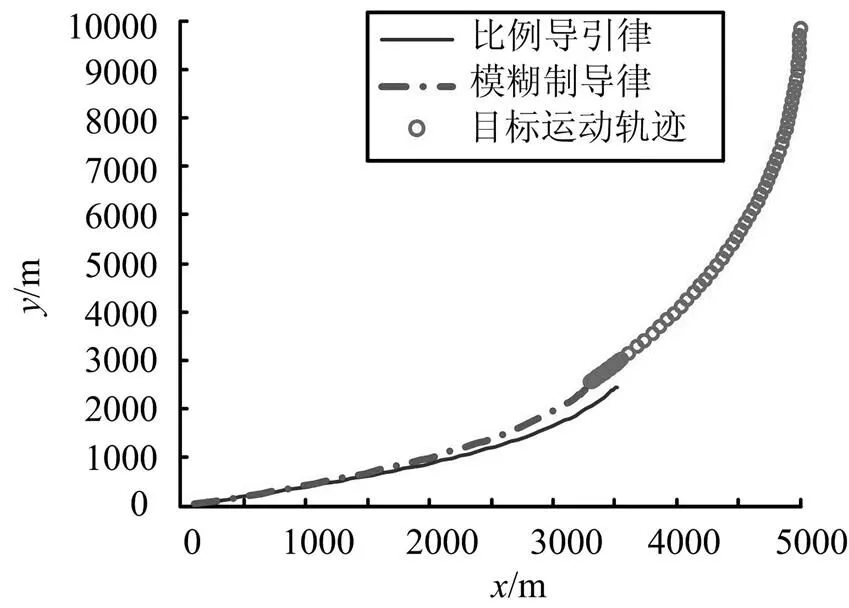
图10 案例3拦截弹与目标二维交战图

a）视线转率

b）过载变化

图11 案例3拦截弹与目标的视线转率及过载变化曲线

d）案例4：目标做变加速度机动，加速度大小正弦变化，变化范围为-200~200 m/s2。仿真结果见图12和图13。

由拦截弹与目标的二维交战图可以看出，当目标做变加速度机动，加速度大小正弦变化，变化范围为-200~200m/s2时，比例导引律未能成功拦截目标，脱靶量较大，为42.159 2 m；模糊制导律能够成功拦截目标，脱靶量为1.574 0 m。与案例3相比，虽然目标的最大机动加速度均为200 m/s2，但是由于目标的机动方式不同，模糊制导律能够有效跟踪目标的机动加速度，产生相应的制导控制指令，抑制拦截弹视线转率发散，从而降低拦截脱靶量。

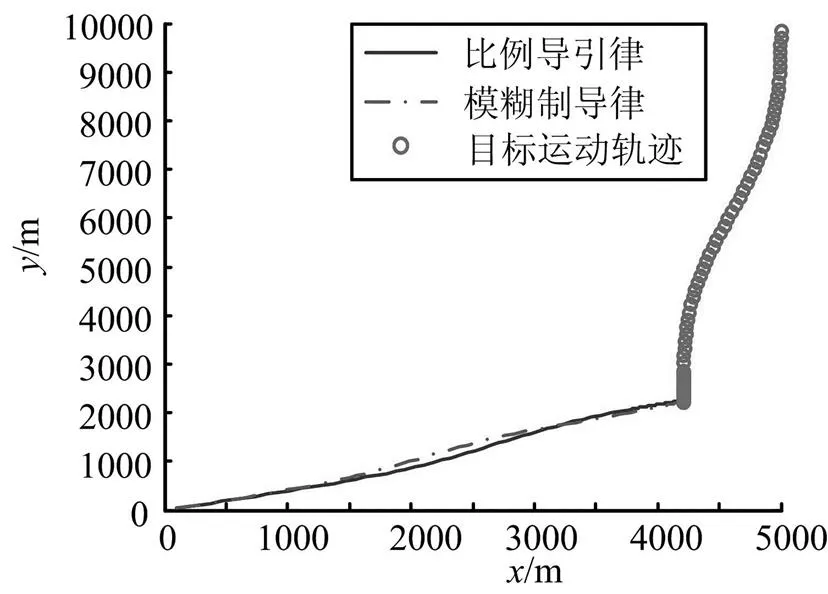
图12 案例4拦截弹与目标二维交战图

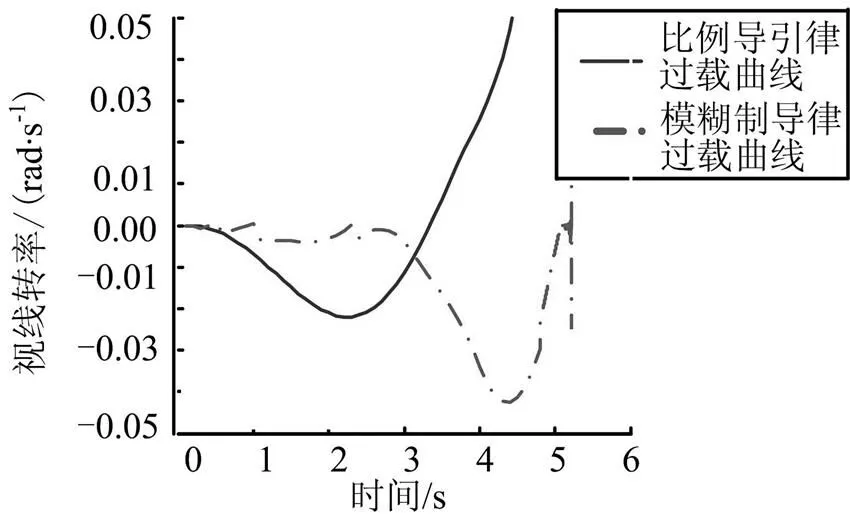
a）视线转率

b）过载变化

图13 案例4拦截弹与目标的视线转率及过载变化曲线

案例1~4比例导引律与模糊制导律拦截结果对比如表2所示。对结果进行分析可以看出，对目标最有利的机动方式为案例3。在案例3中，随着目标的接近，目标的机动加速度越来越大，模糊制导律的需用过载大于了导弹自身的最大可用过载，导致拦截失败。在案例1~4中，基于模糊逻辑的导弹扩展比例导引律相比于传统的比例导引律能够更好地跟踪导弹与目标的视线转率变化，拦截末段视线转率不会发散[7，8]，拦截效果更好。

表2 案例1~4比例导引律与模糊制导律拦截结果对比

4 结 论

随着弹道导弹及临近空间高超声速导弹弹道机动技术的日臻成熟，传统的比例导引律已经无法满足拦截脱靶量的需求。针对临近空间高超声速大机动目标的拦截，本文运用模糊逻辑的方法，制定了模糊控制规则，改进了扩展比例导引律，并且在4种不同的攻防条件下进行了拦截仿真，结果证明基于模糊逻辑的导弹扩展比例导引律能够使导弹在拦截过程中有效跟踪视线转率的变化及目标的机动加速度，拦截末段视线转率收敛，拦截成功概率大大提高。如果将这种制导律装订到拦截弹的制导控制程序中，可以有效控制拦截弹成功拦截临近空间高超声速大机动目标，具有广阔的工程应用前景。

[1] Rajasekhar V，Sreenatha A G. Fuzzy logic implementation of proportional navigation guidance[J]. Acta Astronautica, 2000, 46(1): 17-24.

[2] Lin C L, Hung H Z, et al. Development of an integrated fuzzy-logic-based missile guidance law against high speed target[J]. IEEE Trans. on Fuzzy Systems, 2004, 12(2): 157-169.

[3] Lin C L, Chen Y Y. Design of fuzzy logic guidance law against high-speed target[J]. J. of Guidance, Control and Dynamics, 2000, 23(1): 17-25.

[4] Siouris G M. Missile guidance and control systems[M]. New York: Springer Verlag, 2004.

[5] 李开聪. 模糊制导律与导引品质的关系[D]. 哈尔滨: 哈尔滨工业大学, 2008.

[6] 窦振中. 模糊逻辑控制技术及其应用[M]. 北京: 北京航空航天大学出版社, 1995.

[7] 冯德龙, 杨锁昌, 田再克, 姚运志. 一种改进的扩展比例导引律及其仿真[J]. 火力与指挥控制, 2014(5): 161-163.

[8] 李俊苗. 导弹比例导引规律研究[D]. 沈阳: 沈阳理工大学, 2011.

Extended Proportional Guidance Law of Missile Based on Fuzzy Logic

Shao Jie, Liu Jia-qi, Zhang Chao, Liu Fang, Peng Cheng-yuan

(Beijing Institute of Space Long March Vehicle, Beijing, 100076)

The interception guidance law of the near space hypersonic maneuvering target has always been a challenge in modern guidance and control subject. In this article, the fuzzy logic method was used to improve the extended proportional guidance law, so that during its interception, the missile can track the line of the sight and the target’s acceleration effectively and the rate of rotation of the sight line was convergent during the terminal phase. As a result, the target will be successfully intercepted.

Fuzzy logic; Extended proportional guidance law; Guidance; Missile; Interception

1004-7182(2016)02-0066-06

10.7654/j.issn.1004-7182.20160215

TJ765.2+1

A

2015-06-24；修改日期：2015-10-19

邵 节（1991-），男，硕士研究生，主要从事飞行器总体设计与仿真研究