橡胶扭转减振器滑移转矩计算方法研究*

上官文斌， 聂　均， 魏玉明， 吴启红， 孔占军

(1.华南理工大学机械与汽车工程学院， 广东 广州 510640；2.宁波拓普集团股份有限公司， 浙江 宁波 315800)



橡胶扭转减振器滑移转矩计算方法研究*

上官文斌1,2， 聂均1， 魏玉明1， 吴启红2， 孔占军2

(1.华南理工大学机械与汽车工程学院， 广东 广州 510640；2.宁波拓普集团股份有限公司， 浙江 宁波 315800)

研究了橡胶扭转减振器的滑移转矩计算与实测分析方法。对橡胶扭转减振器的橡胶材料进行了单轴压缩和平面拉伸试验，研究了Mooney-Rivlin和Ogden(N=3)超弹性本构模型用于橡胶扭转减振器滑移转矩计算的适用性。建立了橡胶扭转减振器滑移转矩计算的有限元模型，研究了求解器、质量放大系数、网格属性和加载条件对计算结果和时间的影响。由计算与测试分析的方法，给出了橡胶圈和惯量环、轮毂接触面摩擦系数的确定方法。利用建立的有限元模型，计算分析了2种不同类型的扭转减振器的滑移转矩，并和实测得到的滑移转矩进行了对比分析，计算值和实测值的相对误差小于10%。

扭转减振器； 滑移转矩； 有限元计算； 试验测试

1　概　述

扭转减振器安装在发动机曲轴的前端，主要是为了减少曲轴的扭转振动，降低发动机噪声。常用的扭转减振器有3种：橡胶扭转减振器、硅油扭转减振器和硅油-橡胶复合式扭转减振器。橡胶扭转减振器由于结构简单、可靠性高，在乘用车发动机上得到广泛应用。橡胶扭转减振器主要由轮毂、惯量环、橡胶圈组成，如图1所示，其中轮毂与发动机的曲轴相连，橡胶圈在轮毂与惯量环之间。惯量环一般与驱动发动机前端附件的皮带相连，将发动机的转矩传递给各个附件轮(如水泵轮、空调压缩机轮等)。橡胶圈的形状可以为中间凸出的圆柱形(简称鼓形，如图1(a)所示)，或橡胶圈的形状为简单圆柱形(简称直筒型，如图1(b) 所示)。橡胶扭转减振器橡胶圈作为其弹性元件和阻尼元件，起减振作用。

目前，在扭转减振器减振特性的研究中，对其固有频率特性研究较多[1-3]，而对减振器的另外一个重要性能——惯量环和轮毂之间产生滑移时的滑移转矩研究的较少。在发动机附件大转矩和发动机扭转激励的长期作用下，减振器的轮毂和橡胶圈之间会产生打滑失效现象。因此，扭转减振器滑移转矩是橡胶扭转减振器的一个重要性能参数。在产品开发前期，如何计算橡胶圈的不同结构尺寸、不同压缩比和采用不同的橡胶材料时橡胶扭转减振器的滑移转矩是一项有意义和创新的工作。

图1　扭转减振器Fig.1　Rubber damped torsional vibration damper

Meirelles和Mendes等人[4]建立发动机扭振计算的数学模型，计算中提出橡胶扭转减振器中橡胶圈的动态剪应力不大于0.4 MPa。依据该要求和橡胶减振器的几何尺寸，推算橡胶圈传递转矩小于220 N·m。考虑到橡胶应力软化效应(Mullins效应)[5]、疲劳损伤以及交变激励的影响，扭转减振器的滑移转矩要求往往会增加。对现有市场上常见的扭转减振器进行统计，滑移转矩的值一般要求在400～600 N·m之间。

本文建立了橡胶扭转减振器滑移转矩计算的有限元模型，给出了用于橡胶圈有限元建模的橡胶材料参数的确定方法，探讨了橡胶圈与轮毂和惯量环之间摩擦系数的确定方法。研究了橡胶圈的形状对扭转减振器滑移转矩的影响,建立了扭转减振器滑移转矩计算的有限元模型，对直筒形和鼓形两种橡胶扭转减振器的滑移转矩进行计算分析，并和试验结果进行了对比分析。

2　滑移转矩计算的有限元模型

为了建立橡胶扭转减振器滑移转矩计算有限元模型，需要确定橡胶圈材料本构模型参数、橡胶圈与轮毂和惯量环之间的摩擦系数等。

2.1橡胶圈材料本构模型参数确定

橡胶圈的橡胶材料为天然橡胶加入炭黑等成分混炼成的三元乙丙橡胶，其主要成分是原胶(天然胶EPDM)、炭黑、石蜡油、防老剂和硫磺等。由于填充炭黑材料产生的增强效应，使得橡胶的模量、拉伸强度、撕裂强度、抗疲劳和抗磨损性能大幅高[6]。假设橡胶为连续变形体，工程中常采用唯象理论来准确描述橡胶材料的变形[7]。大量的研究结果表明[8]，8链网络模型能很好地模拟橡胶材料在各种变形模式下的行为，是目前唯象理论适用性最强的橡胶超弹性本构模型[9]。唯象模型的建立，关键在于构造合适的应变能密度函数。目前广泛应变能密度函数有两种，一种是基于应变不变量I1，I2，I3的应变能密度函数，一种是基于主伸长比λ1，λ2，λ3的应变能密度函数[10]。3个应变不变量和3个主伸长比有如下关系：

(1)

式中主伸长比λi与主应变εi之间的关系为

(2)

依据公式(1)和(2)可以推导各个本构模型的应变能密度函数。有限元软件中常用的超弹性本构模型有Neo-Hooke模型、Mooney-Rivlin模型、Yeoh模型、缩减多项式模型(Reduced-Polynomial模型)和Ogden模型[10]。不同模型对不同配方和变形情况，其拟合精度不同。橡胶扭转减振器中的胶圈的变形主要为压缩变形和剪切变形。

为了得到与橡胶圈对应的橡胶材料的本构模型参数，利用单轴压缩试验和平面拉伸试验机，得到橡胶材料的单轴压缩(ET)试验数据和平面拉伸(PT)试验数据。文献[11-12]研究表明，只有单轴试验和平面拉伸的试验数据时，Mooney-Rivlin模型和Ogden(N=3)模型对炭黑填充橡胶的超弹性特性的表征能力最强。

在材料试样单轴压缩和平面拉伸变形过程中，载荷作用方向上的名义应力和主伸长比的关系[12]有以下两种公式Mooney-Rivlin模型为

(3)

Ogden(N=3)模型为

(4)

用于试验的橡胶圈材料的邵氏硬度为70HA。采用橡胶试柱(直径29 mm, 高度12.5 mm)和橡胶试片(长、宽、厚度分别为150，150，2 mm)进行单轴压缩试验和平面拉伸(剪切)试验，试验中记录橡胶变形过程中的力与位移值。

图2　橡胶试验力-位移曲线Fig.2　Measured force versus displacement for rubber specimen

实测的力-位移曲线如图2所示。从图2(a)和(b)可以看出，在单轴压缩和平面拉伸试验中，橡胶材料的力-变形量关系具有强非线性。

依据公式(3)，(4)对试验数据进行处理，将变形量转换成应变，力转换成名义应力。采用最小二乘法方法，拟合试验测试得到的应变和名义应力，和由Mooney-Rivlin模型、Ogden(N=3)模型计算得到的应变和名义应力，由此可以得到Mooney-Rivlin模型和Ogden(N=3)模型中的模型参数[10,13-14]。

试验与拟合的应变-名义应力曲线如图3所示。由图3可知，对所研究的橡胶材料，Mooney-Rivlin模型对单轴压缩试验和平面拉伸试验应变-应力的拟合精度均高于Ogden(N=3)模型。因此，本文采用Mooney-Rivlin模型表征橡胶圈的超弹性特性。拟合得到的Mooney-Rivlin模型的材料常数如表1所示。

图3　橡胶试验数据拟合曲线Fig.3　Measurement and fitted stress versus strain

参数C10C01D1数值0.80160.12690

表中C10和C01为材料常数,无具体含义；D1为体积压缩比，橡胶变形过程中体积几乎不可压缩[10]，取值为0。

2.2橡胶圈与内外环接触属性确定

图4为橡胶圈压入轮毂和惯量环之间的示意图。橡胶圈在一定的外力作用下平滑地压入轮毂和惯量环之间的间隙中，使轮毂和惯量环组成柔性连接体。在有限元建模时，将轮毂、惯量环的表面设置成主面，橡胶的表面设置成从面[15]。

图4　橡胶圈压装图Fig.4　Assemble drawing of rubber ring

在进行减振器的扭转试验时，一般是惯量环固定，在轮毂上施加转矩。转矩由橡胶与惯量环和轮毂之间的摩擦力产生，因而橡胶圈与轮毂、惯量环之间摩擦系数的大小直接影响求解结果的准确性。

扭转减振器中的橡胶圈处于压缩状态，由于其欲恢复到自然状态，因此橡胶圈对惯量环和轮毂有压力N。压力N对摩擦表面产生摩擦力，扭转过程中，橡胶圈2个接触面产生相对运动，摩擦力对扭转减振器产生沿轴线方向转矩T。由于橡胶圈和轮毂、惯量环之间的接触属性相同，而惯量环的半径大于轮毂的半径，相同条件下，惯量环和橡胶圈之间的转矩大于轮毂和橡胶圈之间的转矩，因而在扭转过程中，惯量环与橡胶圈的接触面不发生滑移，滑移仅发生在轮毂与橡胶圈接触面之间。

令μ为摩擦系数，σ为橡胶圈内外表面的应力，S为接触面积，R为扭转减振器轮毂半径，滑移转矩可由下式计算得到

(5)

式中Neq为等效正压力。依据公式(5)可知，若等效正压力Neq恒定，那么转矩T的大小就和摩擦系数μ成正比。

图4中橡胶圈尺寸为：内径107 mm，厚度4 mm，高18 mm，装配完成压缩比为30%。扭转减振器发生扭转滑移时，最大扭转角θmax不超过15°，因此橡胶圈的内表面和外表面由于扭转产生相对位移最大值为14 mm。

为研究压缩过程中正压力Neq的变化，建立如图5所示的有限元模型。以橡胶片表示沿截面展开的橡胶圈，橡胶片的原始厚度为4 mm。为模拟橡胶圈的压入，假定橡胶片的上表面与一金属模具接触，金属模具首先沿负Y方向压缩31%，使其厚度变为2.75 mm，然后上表面的金属模具沿正Z方向平移14 mm。利用建立的模型，计算上模平面所受到的Y方向的正压力。计算得到正压力变化曲线如图6所示。由图6可知，在模具沿Z向平移过程中，正压力基本保持恒定，正压力波动范围保持在1% 以内。

图5　橡胶片正压力验证模型(单位：mm)Fig.5　Model of positive pressure for rubber ring (Unit：mm)

图6　上模平面支反力变化曲线Fig.6　Variation of reaction force for upper mould

由于扭转变形过程中等效正压力Neq基本维持恒定，转矩T的大小就和摩擦系数μ成正比。在初始计算时，假定摩擦系数为μ0，仿真模拟得到滑移转矩为T0。试验测试得到滑移转矩为T,接触面的摩擦系数可由下式计算得到。

(6)

在初始设置过程中，假定摩擦系数μ0=0.1。后文根据试验结果，推算出真实摩擦系数μ。

2.3有限元求解参数确定

本文采用Abaqus显式求解器Abaqus/Explicit求解，其求解方法是在时间域中以很小的时间增量步逐步求解，而无需在每个增量步求解耦合的总体刚度矩阵，因而该求解器能处理更加复杂的接触边界而不会产生收敛问题，并且所需的计算机资源较少[13]。

橡胶圈压入和扭转是一个准静态(quasi-static)过程，在保证求解精度的情况下，通常会引入质量放大系数来缩短求解时间。求解时间可由下式计算得到。

(7)

式中T为求解时间；t为软件中分析步时间；Lmin为最小网格尺寸；λ为每一增量步所对应实际计算时间；材料的弹性模量为E，密度为ρ；N为质量放大系数[16]。

由公式(7)可知，求解时间与最小网格尺寸成反比，与质量放大系数算术平方根成反比。质量放大系数太大，求解过程中会加入太多的动态因素，对求解结果的精度影响最大；质量放大系数太小，求解时间太长[17]。本文初步选择质量放大系数100，1000和10000进行试算。这样求解速度在理论上比没有质量放大的模型提高了至少10倍。

在橡胶扭转减振器受力扭转的过程中，与橡胶圈的变形相比，金属元件的变形忽略不计，因此，在仿真建模时，惯量环、齿环等金属元件假设为刚体。由于扭转减振器中橡胶压缩比较大，通常为30%，线性减缩积分单元在网格会存在严重扭曲变形，对分析精度有影响。本文橡胶圈网格属性为线性减缩积分单元(C3D8R)[15]。

由于橡胶单元在Abaqus/Explicit中采用一阶减缩积分单元(C3D8R)，该单元在数值上存在沙漏问题，所以需要验证求解过程中，系统伪应变能(ALLAE)与系统内能(ALLIE)的比值是否在10%以内。大于10%说明求解过程中沙漏问题严重，求解结果精度较差[18]。在各质量放大系数下，系统伪应变能与系统内能的比值曲线如图7所示。

橡胶圈压入和扭转是一个准静态过程，系统动能(ALLAE)与系统内能(ALLIE)的比值在10%以下才能精确模拟准静态过程[16]。在各质量放大系数下，系统动能与系统内能的比值曲线如图8所示。

图7　伪应变能和内能的比值Fig.7　Ration of pseudo energy and internal energy

图8　动能和内能的比值Fig.8　Ration of dynamic energy and static energy

从图7和8中可以看出，当质量放大系数取1000时，在保证求解精度前提下，可以有效缩短计算时间。在计算时，橡胶圈网格数量为26850，无质量放大系数，求解时间为3 h；质量放大系数为1000时，求解时间为7 min。

2.4摩擦系数确定

在计算图4所示的某款橡胶扭转减振器滑移转矩时，首先加载位移载荷，使橡胶圈压入，然后在轮毂上加载旋转角度载荷。由于滑移扭转角一般小于15°，计算时，旋转角度的最大值设定为0.26 rad(15°)。由于载荷冲击会影响准静态过程的求解精度，计算载荷施加时应平滑加载。在分析步开始和结束时，载荷变化的速度(一阶导数)和加速度(二阶导数)应为0，在Abaqus中以平滑分析步的方式控制载荷的幅值。计算时，初始摩擦系数为0.1，计算得到滑移转矩为162 N·m。

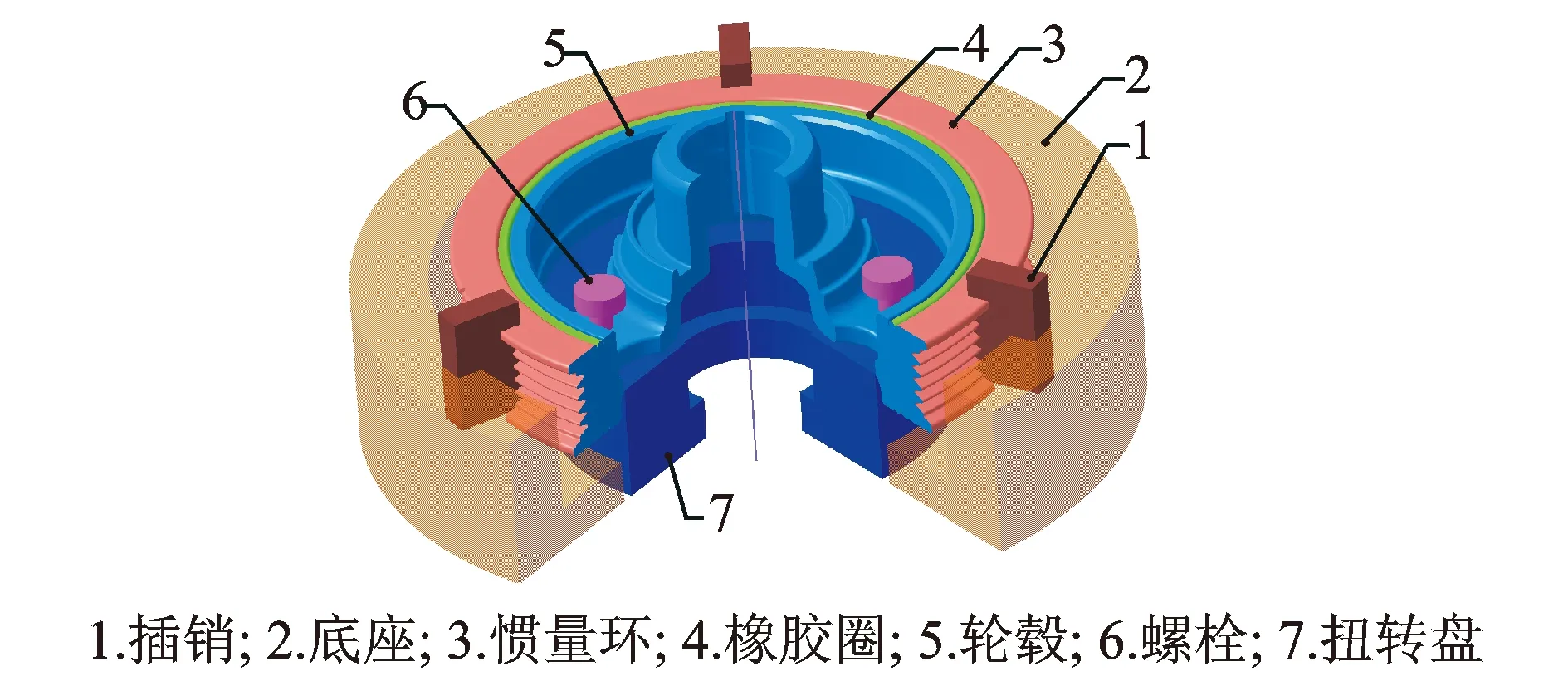
图9　滑移力矩测试装夹图Fig.9　Test rig for measuring slip torque of damper

从生产的产品中随机挑选10个同款扭转减振器，编号为1～10。在H94G2扭力测试机上进行扭转试验，扭转减振器试验装夹如图9所示。基座固定，通过插销固定扭转减振器的惯量环，通过螺栓将轮毂固定在扭转盘上，扭转盘带动轮毂旋转。试验过程中，扭力测试机自动记录转矩和转角数据以及最大转矩。测试得到的10个扭转减振器的滑移转矩如表2所示。

在10组试验数据中选取最小的最大转矩值作为滑移转矩的参考值。从表2中可以看出，10组数据中，6号产品的滑移转矩最小为612 N·m。依据2.2节中方法，摩擦系数为

(8)

在后文的有限元模型中，摩擦系数设置为0.37。

表2滑移转矩测试值

Tab.2Measured slip torque

产品编号12345678910最大转矩/(N·m)733647613656633612678652626622

3　滑移转矩计算与实测

利用第2.2节中建立的有限元模型进行直筒形扭转减振器和鼓形扭转减振器滑移转矩计算分析，然后对同一减振器进行10组转矩测试，对仿真结果和试验数据进行对比，以验证模型的正确性。

3.1直筒形扭转减振器

设计直筒形扭转减振器，为方便加工，忽略惯量环的齿形，其结构如图10(a)所示，加工的产品代号为5977，其橡胶圈的压缩比为33.3%。依据结构图，建立有限元模型如图10(b)所示。为清楚显示模型内部结构，刚体部分仅显示其回转对称的轮廓线。利用图10(b)有限元模型进行滑移转矩计算，滑移转矩的计算值为615 N·m。

选取10个5977试验产品，进行扭转试验，记录转矩和转角数据。绘制转矩-转角曲线如图11所示。从图11中可以看出，直筒形扭转减振器在测试过程中，扭力测试机存在预载过程，转角小于2°时，转矩变化在50 N·m以内。在上升阶段，计算得到曲线和试验数据基本重合，随着转角增加，转矩也近似线性增加。在达到滑移转矩后，由于计算中不考虑动摩擦因素的影响，动摩擦系数和静摩擦系数相等，因而计算转矩达到最大值后不再变化。试验测试得到的各试验产品的滑移转矩如表3所示。

图10　直筒形扭转减振器模型(5977 产品)Fig.10　Model of torsional damper with linear type of rubber spring　(Production No 5977)

图11　直筒形减振器仿真和试验转角-转矩曲线Fig.11　Measured and tested torque versus angle for linear type of rubber ring

Tab.3Measured slip torque for the linear type damper (Production No 5977)

产品编号12345678910最大转矩/(N·m)666588617596609612633593606635

由表3中数据可知，扭转试验最小值为588 N·m，滑移转矩的计算值为615 N·m，计算结果和试验结果相对误差为

(9)

3.2 鼓形扭转减振器

依据3.1中的方法，对鼓形扭转减振器(产品代号E300，橡胶圈的压缩比为36%)的滑移转矩进行计算。 E300产品的CAD模型和有限元模型分别如图12(a)和(b)所示。选取10个E300产品，进行滑移力矩的试验。计算和试验测试得到的转矩-转角曲线如图13所示。

图12　鼓形扭转减振器模型Fig.12　Model for damper of curved type

图13　E300鼓形减振器仿真和试验转角-转矩曲线Fig.13　Measured and tested torque versus angle for curved type damper

从图13中可见，鼓形扭转减振器在测试过程中，转角小于3°时，转矩变化在50 N·m以内，仿真转矩的增长速率明显大于实测曲线。读取试验测试中各个产品的滑移转矩列表于表4。

由图12(b)有限元模型，仿真计算滑移转矩为559 N·m，扭转试验最小值为515 N。仿真值和试验结果误差为

(10)

表4鼓形扭转减振器滑移转矩实测值

Tab.4Measured slip torque

产品编号12345678910最大转矩/(N·m)566541569527526539515542580552

3.3直筒形和鼓形扭转减振器滑移转矩对比

为了比较直筒形和鼓形扭转减振器的滑移转矩之间的关系，利用图12(a)中鼓形扭转减振器毛坯，经机加工处理成对应的直筒形，结构模型如图14(a)所示，橡胶压缩比仍为36%。利用3.1中的计算方法和测试方法，得到的直筒形和鼓形扭转减振器数据转角-转矩曲线如图15所示。

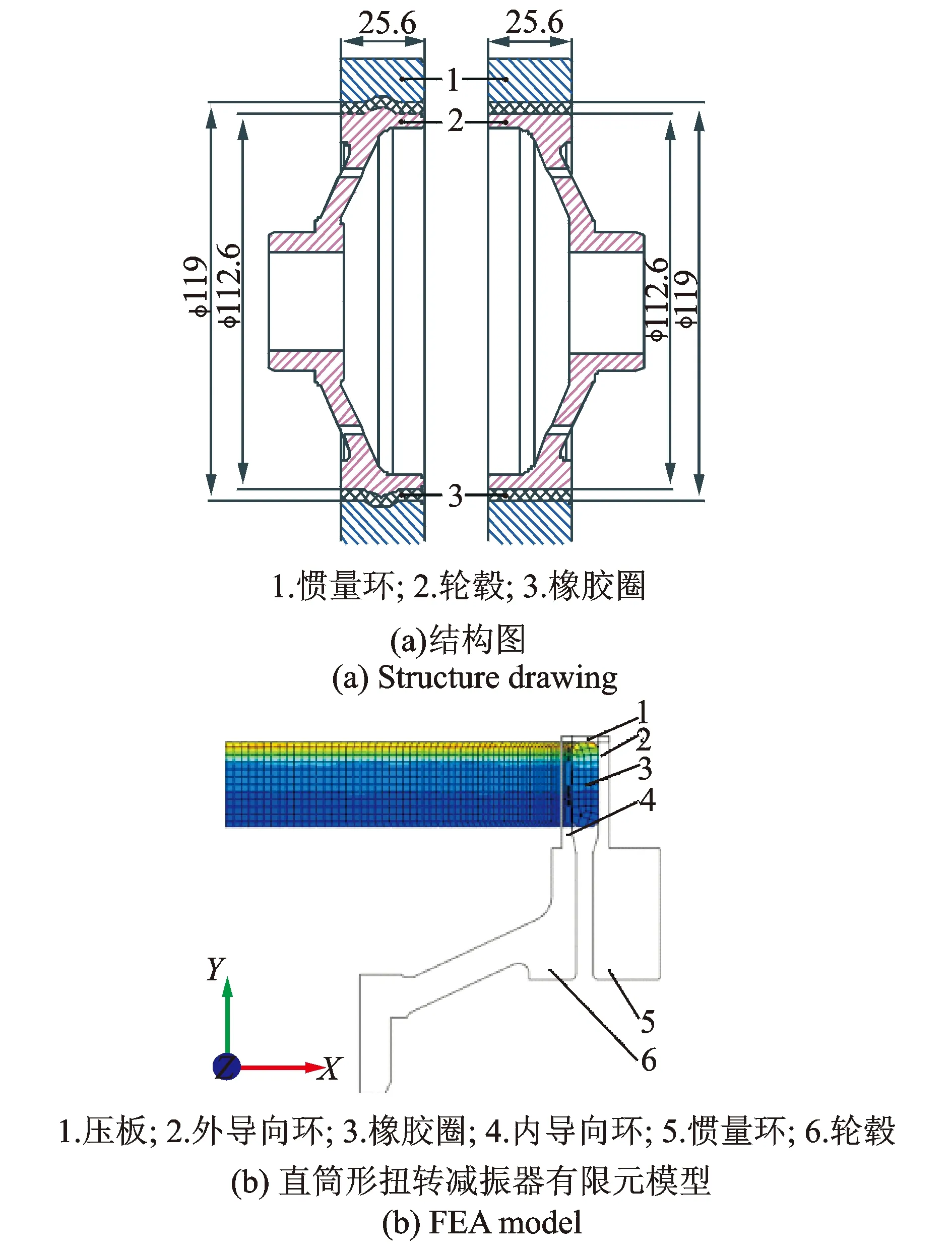
图14　两种结构形式的扭转减振器Fig.14　Two types of dampers

由图15可见，在转角小于5°时，计算的转矩比实测转矩斜率大，鼓形减振器扭转刚度大于直筒形减振器的扭转刚度，且鼓形扭转减振器的滑移转矩大于直筒形扭转减振器的滑移转矩。测试得到的鼓形、直筒形扭转减振器滑移转矩如表5所示。

图15　E300产品转角-转矩曲线的计算值和试验值Fig.15　Measured and calculated torque versus angle for E300

产品编号12345678910直筒形/(N·m)488440499441479484431443456436鼓形/(N·m)566541569527526539515542580552

从表5可以看出，鼓形扭转减振器10个产品的滑移转矩均大于500 N·m，利用3.1与3.2节中类似的计算方法，计算得到的鼓形扭转减振器滑移转矩仿真值为559 N·m。直筒形扭转减振器10个产品的滑移转矩均小于500 N·m，计算得到的直筒型扭转减振器滑移转矩仿真值为458 N·m。计算值和试验值吻合得较好。

4　小　结

(1) 测试了扭转减振器橡胶材料的应力-应变曲线，利用Mooney-Rivlin和Ogden(N=3)本构模型对测试得到的橡胶材料应力-应变曲线进行拟合，结果表明，Mooney-Rivlin模型可以较好地表征扭转减振器中橡胶材料的弹性特征。

(2) 基于橡胶圈扭转变形过中等效正压力维持恒定的假设，提出了橡胶圈与金属接触面摩擦系数的确定方法。

(3) 建立了扭转减振器滑移转矩计算的有限元模型，分析了有限元模型的参数对求解时间和计算结果的影响。利用建立的有限元模型，计算分析了直筒型和鼓型扭转减振器的滑移转矩，并和试验测试值进行了对比分析，试验结果和计算结果相对误差小于10%。计算与试验研究了相同尺寸的扭转减振器，其橡胶圈的形状对滑移转矩的影响。

(4) 本文提出的橡胶扭转减振器滑移转矩的计算方法和试验测试方法可以用于扭转减振器滑移转矩的设计与计算分析。

[1]Mendes A S, Meirelles P S, Zampieri D E. Analysis of torsional vibration in internal combustion engines: modelling and experimental validation[J]. I. Mech. E., Part K:Journal of Multi-Body Dynamics, 2008, 222 (2): 155—178.

[2]Shangguan Wen-Bin, Pan Xiao-Yong. Multi-mode and rubber-damped torsional vibration absorbers for engine crankshaft systems[J]. International Journal of Vehicle Design, 2008,47:176—188.

[3]上官文斌,魏玉明,赵旭,等. 橡胶阻尼式扭转减振器固有频率计算与测试方法的研究[J].振动工程学报,2015,28(4): 550—559.

Shangguan Wen-bin, Wei Yu-ming, Zhao Xu, et al. A study on method of calculation and measurement for natural frequency of torsional vibration rubber damper[J]. Journal of Vibration Engineering, 2015,28(4): 550—559.

[4]Meirelles P S, Zampieri D E, Mendes A S. Mathematical model for torsional vibration analysis in internal combustion engines[C]. 12th IFToMM World Congress. Besancon France, 2007,6: 18—21.

[5]Marckmann G, Verron E, Gornet L. A theory of network alteration for the Mullins effect[J].Journal of the Mechanics and Physics of Solids, 2002, 50(9): 2011—2028.

[6]Fukahori Y. New progress in the theory and model of carbon black reinforcement of elastomers[J].Journal of Applied Polymer Science, 2005, 95(1): 60—67.

[7]何平笙,杨海洋,朱平平.橡胶高弹性大形变的唯象理论[J]. 化学通报,2006,01:70—73.

He Pingsheng, Yang Haiyang, Zhu Pingping. The phenomenological theory of rubber in large elastic deformation[J]. Chemistry, 2006, 01: 70—73.

[8]谭江华,罗文波.橡胶材料分子链网络本构模型的研究进展[J].材料导报,2008,22(7):31—34.

Tan Jianghua, Luo Wenbo. Advances in studies on molecular chain-network based constitutive models of rubber materials[J]. Materials Review, 2008, 22(7): 31—34.

[9]李旭.轮胎胶料在较大变形范围内超弹性性能与填充和共混的相关性研究[D].合肥:中国科技大学,2012,05: 23—30.

Li Xu. Study on the reinforcement and blend dependence of hyperelasticity of tire rubbers under the moderate finite deformation[D]. Hefei: University of Science and Technology of China, 2012, 05: 23—30.

[10]何小静,上官文斌.橡胶隔振器静态力-位移关系计算方法的研究[J].振动与冲击,2012,31(11):91—97.

He Xiao-jing, Shangguan Wen-bin. Calculating methods for force versus displacement relation of a rubber isolator[J]. Journal of Vibration and Shock, 2012,31(11):91—97.

[11]胡小玲,李明,刘秀,等.炭黑填充橡胶超弹性力学性能的三维有限元模拟[J].固体力学学报,2013,10: 117—121.

Hu Xiaoling, Li Ming, Liu Xiu, et al. 3D finite element modeling of the hyperelastic mechanical behavior of CB-filled rubber[J]. Chinese Journal of Solid Mechanics, 2013, 10: 117—121.

[12]杨晓翔.非线性橡胶材料的有限单元法[M].北京:石油工业出版社,1999.

Yang Xiaoxiang. Finite Element Method of Nonlinear Rubber Materials[M]. Beijing：Petroleam Industry Press， 1999.

[13]潘孝勇,上官文斌,柴国钟,等.基于超弹性、分数导数和摩擦模型的碳黑填充橡胶隔振器动态建模[J].振动与冲击,2007,10: 6—10.

Pan Xiao-yong, Shangguan Wen-bin, Chai Guo-zhong， et al. Dynamic modeling for carbon-filled rubber isolators based on hyperelasticity, fractional derivative and a generalized frictional model[J]. Journal of Vibration and Shock, 2007, 10: 6—10.

[14]庒茁,张帆. ABAQUS非线性有限元分析与实例[M].北京:科学出版社,2005.

Zhuo Zhuan, Fan Zhang. ABAQUS Nonlinear Finite Element Analysis and Examples [M]. Beijing: Beijing Academic Press, 2005.

[15]徐宏彬,丁淑蓉,万继波,等.平板轧制过程的三维数值模拟研究[J].力学季刊,2013,12: 546—556.

Xu Hong-bin, Ding Shu-rong, Wan Ji-bo, et al. Three-dimensional numerical simulation of strip rolling process[J]. Chinese Quarterly of Mechanics, 2013, 12: 546—556.

[16]ABAQUS Inc. ABAQUS Analysis User’s Manual[M]. Version 6.12,2010.

[17]Belytschko T, Liu W-K, Kennedy J M. Hourglass control in linear and nonlinear problems[J]. Computer Method in Applied Mechanics and Engineering, 1984(43):255—276.

A research on the methods for calculation slip torque of rubber damped torsional vibration absorbers

SHANGGUANWen-bin1,2,NIEJun1,WEIYu-min1,WUQi-hong2,KONGZhan-jun2

(1. School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510641, China;2. Ningbo Tuopu Group Co., Ltd, Ningbo 315800, China)

In this paper, the calculation and experimental methods for obtaining the slip torque of rubber damper Torsional Vibration Absorber (TVA) are presented. Firstly, the uniaxial compression test and the plane tension test for the rubber materials used for TVA are carried out, and two hyper-elastic constitutive models, Mooney-Rivlin and Ogden (N=3), are used to find the feasibility of characterizing the rubbers properties. The finite element model for calculating the slip torque of a TVA is presented. The influence of solution methods and the parameters in the model, such as mass scaling factor, mesh property and loading condition, on the estimating time and calculated results are described and discussed. The method for obtaining the friction coefficient between the rubber and hub or inertia ring in a TVA is proposed based on calculation and experiment method. Two types of TVA are taken as studying examples. The shape of rubber ring in one type of TVA is cylinder, whereas the shape in another type of TVA is a cylinder with the middle part of the outer surface is convex. The slip torques of the two type of TVA are calculated and compared with the experiment, and it is shown that the relative error between calculation and experiment is less than 10%.

rubber damped torsional vibration absorber; slip torque; finite element calculation; experiment

2014-07-05；

2015-12-07

国家自然科学基金资助项目(51275175，11472107)

TH703.63； O242.82

A

1004-4523(2016)01-0096-09

10.16385/j.cnki.issn.1004-4523.2016.01.013

上官文斌(1963—),男,教授。电话: 18820072208; E-mail:sgwb@163.com