矩形多项式矩阵的正则化与零点配置
2016-09-21张国山林竹雨
张国山,林竹雨
(天津大学 电气与自动化工程学院,天津 300072)
矩形多项式矩阵的正则化与零点配置
张国山,林竹雨
(天津大学 电气与自动化工程学院,天津 300072)
考虑一个行满秩的矩形多项式矩阵,研究通过补偿一个矩形多项式矩阵使其成为方阵,并保持补偿后矩阵没有无穷远零点且可以实现有限零点任意配置,该问题可以称之为正则化问题.通过变换,该问题可以转化为广义系统的极点配置问题.运用多项式矩阵理论与广义系统理论,给出满足期望特性的补偿矩阵(正则化矩阵)存在的充要条件和构造方法.
矩形多项式矩阵;补偿;正则化;无穷远零点;广义系统理论
多项式矩阵描述(polynomial matrix description ,简称PMD)的控制系统是研究控制系统的重要方法之一,目前已经形成了独立的理论体系[1],并与状态空间方法共同发展.通常是在正则的前提下研究一个PMD系统,因为正则性保证了系统方程的解的存在性和唯一性.如果从PMD的角度,将一个多项式矩阵理解为系统的状态系数矩阵,其零点(有限零点和无穷远零点)对应于其所描述的系统的极点(有限极点和脉冲模).一个矩形多项式矩阵可以认为是矩形系统状态的系数矩阵,这样的系统不满足正则性条件,因而其状态无解或不具有唯一解.将一个矩形系统补偿成为一个正则系统相当于将一个矩形矩阵补偿为满秩的方阵,因此研究矩形多项式矩阵的正则化及其零点配置问题,相当于研究矩形系统正则性与极点配置问题.
在多项式矩阵及其描述的系统零极点的研究方面,文献[1]介绍了PMD的基本理论;文献[2]基于状态映射研究了正则多项式矩阵的无穷远极零点个数;文献[3]给出了正则多项式矩阵没有无穷远零点的一个充要条件.以上均为对正则多项式矩阵的研究,在与广义系统相关研究方面,文献[4-5]研究了矩形广义系统的脉冲能控能观及反馈问题;文献[6]研究了基于动态补偿的矩形广义系统的正则化,能控能观性与极点配置问题;文献[7]研究了任意一个多项式矩阵的特征结构;文献[8]研究了使任意一个多项式矩阵最高次的系数矩阵满秩的方法;文献[9]研究了由任意一个行满秩的矩形多项式矩阵构造一个单模阵的方法.受文献[9]启发,研究一个行满秩的矩形多项式矩阵通过某种补偿使其成为具有我们期望特性的矩阵,是一个值得研究的问题.而通过增加矩形多项式矩阵的行数,将其扩展成为一个方形满秩矩阵,是一种有效和可行的补偿方法.
笔者将基于多项式矩阵理论与广义系统理论,对于一定条件下的行满秩多项式矩阵,通过增加其行数将其补偿成为满秩方阵,使其没有无穷远零点而实现有限零点的任意配置,且补偿矩阵的次数低于原矩阵的次数,这与正常系统状态反馈控制的观点相统一,即补偿部分相当于线性系统的状态反馈.特别地,为了对应系统的稳定性,可将其零点配置于左半复平面,即配置成一个Hurwitz矩阵.由于高次多项式矩阵的特征值配置过于复杂,笔者通过多项式矩阵的一种线性化表示[10],即在保持其特征值及某些结构特性不变的前提下,通过扩大其维数将其转化为一次多项式矩阵,然后借助于广义系统理论,获得其零点任意配置的充要条件与配置方法.按所给多项式矩阵的次数,将分为一次和任意次两种情况进行讨论,分别给出对应的方法和结果,最后通过数值算例说明所得结果的合理性.
1 问题的提出
设P(s)∈n×n[s]为任一正则的多项式矩阵,则P(s)可以表示为
(1)
其中:Pμ≠0,μ为P(s)元素中的最高次数(以下简称P(s)的次数),Pi∈n×n,i=0,1,…,μ为各次数的系数矩阵.P(s)正则意味着detP(s)≠0.P(s)的零点(包括有限零点和无穷远零点)定义为使P(s)的秩下降的点[11]. 判定P(s)的无穷远零点的方法为:取变换λ=1/s,则Q(λ)=P(1/λ)在λ=0处的零点就是P(s)在s=处的零点,且二者零点重数相同(按Smith-McMillan标准形定义[1]). 设
(2)
dP(s)=degdetP(s),
(3)
且设P(s)的无穷远零点个数为z,则z,rp(s)和dp(s)的关系为引理1.
引理1[2]z=rp(s)-dp(s).
引理1表明,P(s)没有无穷远零点当且仅当rp(s)=dp(s).
考虑一个矩形多项式矩阵P1(s)∈p×n[s],其中p (4) 没有无穷远零点,且有限零点实现任意配置. 为了与线性系统反馈控制理论相对应,要求P2(s)的次数小于P1(s)的次数.由于多项式矩阵形式的系统极点配置问题尚未有有效的解决方法,论文首先给出多项式矩阵的一种线性化形式,然后对其线性化形式,给出其零点任意配置的条件与方法. 分两种情况讨论所得的结果:(1)P1(s)为一次多项式矩阵的情形,此时P1(s)可以认为是矩形广义系统的系数矩阵,利用广义系统理论给出相应的结果;(2) P1(s)为(大于1次的)任意次多项式矩阵的情形,首先给出其线性化表示,然后利用上一种情形的结果,给出一般性的结果及P2(s)的构造方法. 2.1P1(s)为一次多项式矩阵的情形 首先考虑P1(s)=P1s+P0∈p×n[s],P (5) (6) 时,广义系统(E,A,B)脉冲能控. 引理4[4]P1(s)=P1s+P0没有无穷远零点当且仅当(6)成立. 定理1给定一个P1(s)=P1s+P0∈p×n[s],p 证明由广义系统中的反馈和极点配置理论,按分解式(5),存在一个反馈矩阵F∈(n-p)×p,使闭环系统(E,A+BF,B)无脉冲且有限极点可任意配置,进而,矩阵sE-(A+BF)没有无穷远零点且有限零点可任意配置当且仅当(E,A,B)R-能控和脉冲能控,即(6)成立.又因为 (7) (8) 推论1对于P1(s)=P1s+P0∈p×n[s],下面几个表述是等价的: 1) P1(s)=P1s+P0没有有限零点和无穷远零点. 2) 广义系统(E,A,B)是R-能控和脉冲能控的,其中E,A,B由(5)给出. 3) rank(P1s+P0)=P,∀s∈且). 2.2P1(s)∈p×n[s]为任意次多项式矩阵的一般情形 考虑任意的矩形多项式矩阵P1(s)∈p×n[s],P (9) 其中:Pμ≠0,μ>1,Pi∈p×n为各次数的系数矩阵,i=0,1,…,μ. (10) 其中:Pi,a∈p×p,i=0,1,…,μ;Pj,b∈p×(n-p),j=0,1,…,μ-1.利用文献[9-10],将(9)扩展成一种广义系统模型结构,可以认为是由(9)导出的一种线性化表示,令 (11) 定理2对于(9)中的P1(s)及其导出的线性化形式(11),存在一个反馈矩阵F∈(n-p)×μp,使闭环系统(E,A+BF,B)无脉冲且有限极点可任意配置的充要条件是 (12) 进而,如果(12)成立,可求出一个次数小于μ的多项式矩阵P2(s),使(4)没有无穷远零点且有限零点可以任意配置,其中P2(s)的表达式将在定理证明中给出. 下面构造P2(s). 从上面证明得到,系统(E,A+BF,B)无脉冲且有限极点可任意配置等价于矩阵 (13) 没有无穷远零点且有限零点可任意配置.设单模阵 (14) 则 (15) 其中 Pa(s)=Pμ,asμ+Pμ-1,asμ-1+…+P0,a,Pb(s)=Pμ-1,bsμ-1+Pμ-2,bsμ-2+…+P0,b, (16) (17) (18) (19) 其中 (20) 且P2(s)∈(n-p)×n,即P2(s)取矩阵的前n-p行,即 (21) detP(s)=αdet[sE-(A+BF)], (22) 其中:α为非零系数,故P(s)与矩阵[sE-(A+BF)]有相同的有限零点,因为[sE-(A+BF)]的有限零点可以任意配置,故P(s)的有限零点可以任意配置. 接下来证明P(s)没有无穷远零点.因为矩阵[sE-(A+BF)]没有无穷远零点,由引理1及(22),有 dP(s)=degdet[sE-(A+BF)]=rank(E)=(μ-1)P+rank(Pμ), (23) 由(2)和(21)可得 (24) 则由(23)和(24)得rP(s)≤dP(s),又rp(s)≥dp(s),所以rp(s)=dp(s).故由引理1,P(s)没有无穷远零点. 综上,P(s)没有无穷远零点且有限零点可任意配置.故存在一个次数小于μ的多项式矩阵P2(s)∈(n-p)×n[s],使P(s)没有无穷远零点且有限零点可任意配置,等价于存在一个反馈矩阵F∈(n-p)×μp,使闭环系统(E,A+BF,B)无脉冲且有限极点可任意配置,又等价于(12)成立.P2(s)的表达式由(21)给出.证毕. 则 则 笔者分别给出了一次和高次矩形多项式矩阵补偿成一个没有无穷远零点且有限零点可以任意配置的方法,并利用其导出的线性化形式,分别推导了充要条件.实际上,按线性(广义)系统理论,论文方法不仅可以实现矩形多项式矩阵任意极点配置,也可以实现对应系统稳定或其他需要的特性.而从非正则多项式矩阵本身出发,给出通过补偿多项式矩阵使其正则且具有期望零点的条件和方法,是值得进一步研究的课题. [1]郑大钟. 线性系统理论[M]. 2版. 北京: 清华大学出版社, 2002. [2]BELUR M N, PRAAGMAN C. Impulsive solutions, inadmissible initial conditions and pole/zero structure at infinity[C]// 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC), Orlando, Florida, Dec, 2011, 1528-1533. [3]HENRION D Z, NIGA J C. Detecting infinite zeros in polynomial matrices[J]. IEEE Transactions on Circuits and Systems Part 2: Express Briefs, 2005, 52(11): 744-745. [4]ISHIHARA J Y, TERRA M H. Impulse controllability and observability of rectangular descriptor systems[J]. IEEE Transactions on Automatic Control, 2001, 46(6): 991-994. [5]HOU M. Controllability and elimination of impulsive modes in descriptor systems[J]. IEEE Transactions on Automatic Control, 2004, 49(10): 1723-1729. [6]ZHANG G. Regularizability, controllability and observability of rectangular descriptor systems by dynamic compensation[C]// Proceedings of the American Control Conference, Minneapolis, Minnesota, June, 2006, 4393-4398. [7]VAN DOOREN P, DEWILDE P. The eigenstructure of an arbitrary polynomial matrix: computational aspects[J]. Linear Algebra and its Applications, 1983, 50: 545-579. [8]KASE W.Regularization for polynomial matrices and its application to descriptor systems[C]//IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, IEEE, 2012: 2427-2432. [9]EISING R. Polynomial matrices and feedback[J]. IEEE Transactions on Automatic Control, 1985, 30(10): 1022-1025. [10]TERAN F D, DOPICO F M, MACKEY D S. Fiedler companion linearizations for rectangular matrix polynomials[J]. Linear Algebra and its Applications, 2012, 437(3): 957-991. [11]MACIEJOWSKI J M. Multivariable feedback design[M]. New York: Addison Wesley, 1989. [12]杨冬梅, 张庆灵, 姚波, 等. 广义系统[M]. 北京: 科学出版社, 2004. (责任编辑朱夜明) Regularization and zero assignment of rectangular polynomial matrices ZHANG Guoshan, LIN Zhuyu (School of Electrical Engineering and Automation, Tianjin University, Tianjin 300072, China) For a given rectangular polynomial matrix with full row rank, the problem that how to compensate it to a square polynomial matrix by adding another rectangular polynomial matrix was investigated, which made the square polynomial matrix have no infinite zeros and achieve arbitrary finite zero assignment. The problem could be named as the regularization problem. It could be transformed into an equivalent problem about pole assignment of descriptor systems. By using polynomial matrix and descriptor system theories, the necessary and sufficient condition were obtained for the existence of the compensated matrix, and a method of constructing such a compensated matrix was presented. rectangular polynomial matrices; compensation; regularization; infinite zeros; descriptor system 10.3969/j.issn.1000-2162.2016.05.001 2016-01-16 国家自然科学基金资助项目(61473202) 张国山(1961-),男,吉林农安人,天津大学教授,博士生导师,博士. O231 A 1000-2162(2016)05-0001-072 主要结果
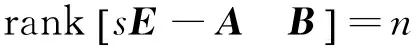
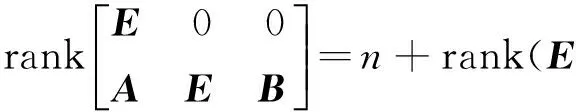
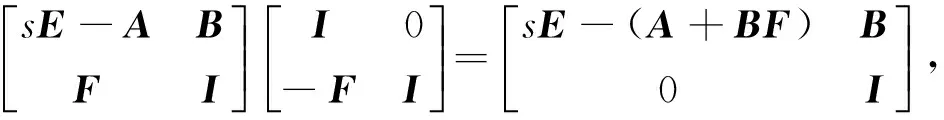
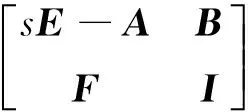
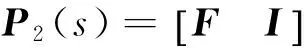
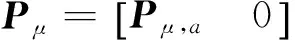
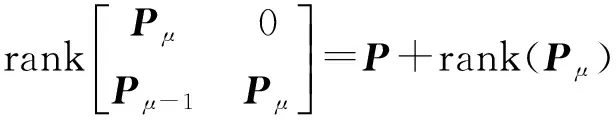
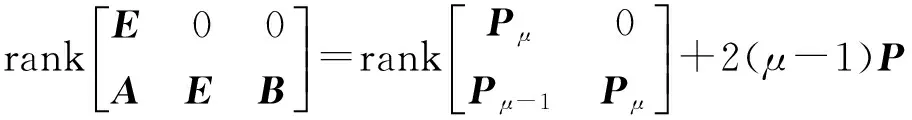
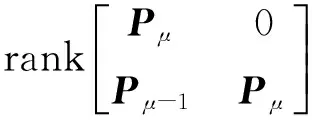
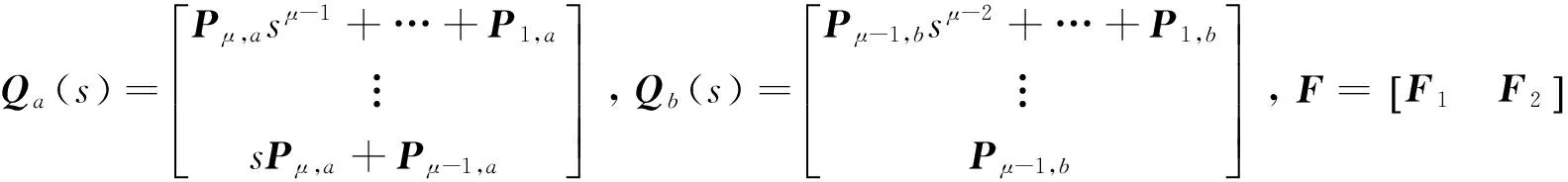
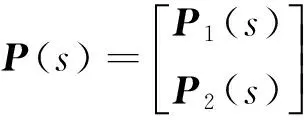
3 数值算例
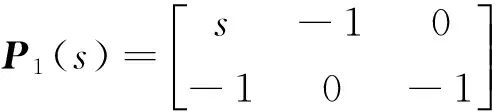
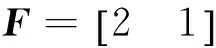
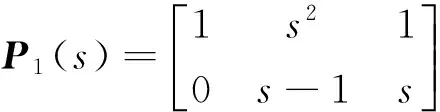
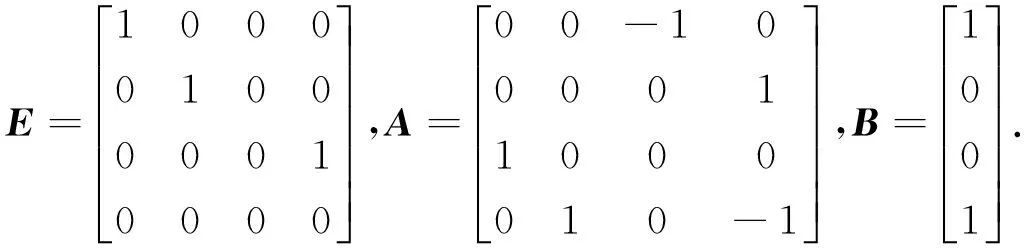
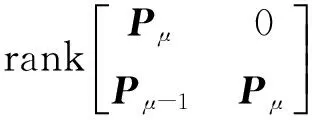

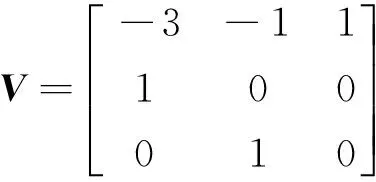
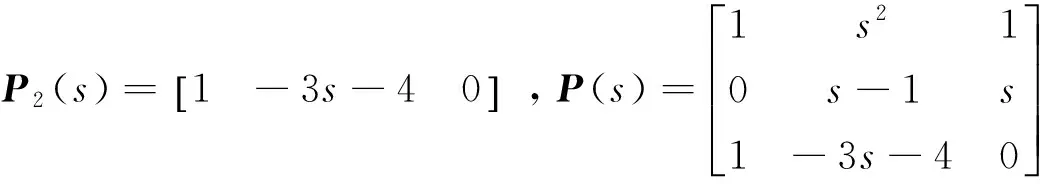
4 结束语
