二阶锥规划求解的新光滑牛顿算法

刘瑞娟, 吴业军 , 张　勇

(南京工程学院 数理部，江苏 南京 210067)



二阶锥规划求解的新光滑牛顿算法

刘瑞娟, 吴业军 , 张勇

(南京工程学院 数理部，江苏 南京 210067)

研究一个新的求解二阶锥规划的光滑牛顿法,算法采用一个新的价值函数,同时利用一个扰动的牛顿方程去获得搜索方向.在不需要满足严格互补的条件下,证明算法是全局和局部二次收敛的,最后数值实验表明算法是有效的.

二阶锥规划；光滑牛顿法；全局收敛；二次收敛

论文考虑如下二阶锥规划问题

(1)

其中：A∈Rm×n,c∈Rn,b∈Rm,Kn⊂Rn是n维的二阶锥，其定义为

(2)

其中：‖·‖表示向量的欧式范数.(P)的对偶问题定义为(D),即下式

(3)

二阶锥规划在控制、金融、组合优化等诸多领域有着广泛的应用，是数学规划领域备受关注的一个方向[1-2].光滑牛顿法是求解二阶锥规划最有效的方法之一，这类方法将二阶锥规划问题等价转化成一个单参数光滑方程，然后利用牛顿法去求解该方程，当参数趋于零时，即可得到二阶锥规划的最优解.Chi等[3-4]基于不同的光滑函数，给出了求解二阶锥规划的光滑牛顿法，并证明了算法的全局与局部二阶收敛性质.Fang等[5-6]、Tang等[7-10]基于不同的光滑函数对二阶锥规划的光滑算法做了进一步的研究.受已有文献的启发，论文给出了一个新的求解二阶锥规划的光滑算法，在不需要满足严格互补条件下，证明了算法是全局和局部二次收敛的.

1　预备知识

为了简单起见，对任意的x,y,z∈Rn，用(x,y,z)表示(xΤ,yΤ,zΤ)Τ.

其中：i=1,2,ϖ∈Rn-1是满足‖ϖ‖=1的任意向量.

众所周知,光滑牛顿法依赖于光滑函数. 论文采用文献[6]提出的光滑函数,定义如下

(4)

下面定理给出了光滑函数φ的一些性质，其具体证明见文献[7]中的定理3.3.

定理1设(μ,x,s)∈R++×Rn×Rn且φ(μ,x,s)由(4)定义，则下面结论成立

(i) 对于任意的μ>0, φ(μ,x,s)全局Lipschitz连续且处处强半光滑.此外，φ(μ,x,s)在任意的(μ,x,s)∈R++×Rn×Rn处连续可微且雅格比矩阵为

其中

2　算法描述

假设1(P)和(D)严格可行.

在假设1下，(P)和(D)都有最优解且最优值相等[1]，并且二阶锥规划等价于其KKT条件

Ax=b,

对任意z∶=(μ,x,y)∈R+×Rn×Rm，定义函数H(z):R+×Rn×Rm→R+×Rm×Rn如下

(5)

其中

(6)

由(5)和(6)可知z*∶=(μ*,x*,y*)是H(z)=0的解当且仅当(x*,y*,c-AΤy*)满足最优性条件(3),即(x*,y*,c-AΤy*)是(P)和(D)的最优解. 下面定理给出H(z)的雅各比矩阵及其可逆条件，其具体证明可参见文献[7]中的引理4.1.

定理2设z∶=(μ,x,y)∈R+×Rn×Rm且H:R1+n+m→R1+m+n,则有

(i)H(z)是R1+n+m上的全局Lipschitz连续函数且处处强半光滑，并且在任意的(μ,x,y)∈R++×Rn×Rm处连续可微，其雅各比矩阵为

其中

(ii) 如果矩阵A行满秩，则对任意的μ>0,有H′(z)可逆.

对任意的z∶=(μ,x,y)∈R+×Rn×Rm，一般采用如下价值函数G1(z)∶=‖H(z)‖2或者G2(z)∶=‖H(z)‖.而论文采用了一个新的价值函数，其定义如下

(7)

下面给出算法的具体描述.

算法1(二阶锥规划的光滑牛顿法)

步骤0取常数δ,σ∈(0,1), μ0∈R++， 选取任意的初始点x0∈Rn,y0∈Rm.令z0∶=(μ0,x0,y0). 取常数τ,γ∈(0,1)，使得γ<μ0且τ+γ<1.令 k∶=0.

步骤1如果‖H(zk)‖=0,则停止迭代.

步骤2令

(8)

其中

(9)

求解方程组

(10)

得到搜索方向Δzk∶=(Δμk,Δxk,Δyk)∈R×Rn×Rm.

步骤3令lk是使得下式成立的最小值

(11)

令αk∶=δlk.

步骤4令zk+1∶=zk+αkΔzk和k∶=k+1.转步骤1.

注传统的光滑算法[3-10]通常利用如下牛顿方程去获得搜索方向

(12)

而算法采用了一个扰动的牛顿方程(10)去获得搜索方向.显然，如果取τ=0，则(10)即变为传统的牛顿方程(12).

引理1令Λk由(9)定义，如果μk≥0,则有

(13)

证明因为

故‖H(zk)‖≤G(zk). 又因为‖Γ(zk)‖≤G(zk), 故可知

这表明对任意的k≥0, ‖Λk‖≤τ,并且‖Λk‖≤τG(zk)2.因此结论成立.

引理2设βk,Λk由(9)定义，则对任意的k≥0,有

(14)

证明因为min{1,ξ2}≤ξ对任意的ξ≥0都成立，故由(9)可得

进而可知结论成立.

定理3假设A行满秩，对所有的k≥0，如果zk=(μk,xk,yk)∈R++×Rn×Rm可由算法1产生，则zk+1可由算法1产生，并且zk+1∈R++×Rn×Rm.

(15)

对任意的α∈(0,1], 定义

则Fk(α)=ο(α),这是因为Γ在任意的zk∈R++×R2n处连续可微.因此，对任意的α∈(0,1],有

(16)

因此，由(15)和(16)可得

(17)

因此，zk+1可由算法1产生，并且zk+1∈R++×Rn×Rm. 证毕.

引理3假设点列{zk=(μk,xk,yk)}由算法产生，则对任意的k≥0,有μk≥βk.

因此，由数学归纳法可得对任意的k≥0，有μk≥βk.

3　算法的收敛性分析

由引理3可知，对任意的k≥0有μk≥βk.故μ*≥μ0β*>0,从而由定理2知H′(z*)存在且可逆.因此，对于充分大的k，令Δzk=(Δμk,Δxk,Δyk)∈R×Rn×Rm为下面方程组的解

在上式两端取极限，可知

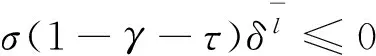
下面分析算法1的局部收敛性质.为此，作如下假设

假设2假设z*满足非奇异条件，即所有的V∈∂H(z*)都是非奇异的.

引理4假设Υk由(9)定义，则对于充分大的k，有‖Υk‖=Ο(‖H(zk)2‖).

(18)

进一步，由H的定义可知μk≤‖H(zk)‖并且‖Γ(zk)‖≤‖H(zk)‖.因此

进而由(14)和(18)可知对于充分大的k，有

定理5(局部收敛性质)假设矩阵A行满秩并且z*是算法1产生的迭代点列{zk}的任意聚点.如果假设2成立，则{zk}二次收敛到z*,即‖zk+1-z*‖=Ο(‖zk-z*‖2).

证明利用引理4，类似于文献[11]中定理8的证明可以证得结论成立，此处省略.

4　数值实验

为检验算法1的实算效果，用Matlab7.0.1编程在电脑上做数值实验.在所有的实验中，选择x0=e∈Rn,y0=0∈Rm作为初始点.参数选择为μ0=0.01, σ=0.25, δ=0.85, γ=0.001, τ=0.25.终止准则为‖H(zk)‖≤10-6.

测试问题是随机生成的规模n=(2m)从100到800不等的二阶锥规划问题,每个规模的问题生成10个，共生成80个测试问题， 计算结果列于表1.其中AIT和ACPU分别表示算法1求解10个问题所需的迭代次数和CPU时间(单位：s)的平均值，“AFV”表示算法1终止时10个测试问题的‖H(zk)‖的平均值.从表1可以看出算法对求解较大规模的二阶锥规划问题是稳定有效的.

表1　算法1求解不同测试问题的结果

[1]ALIZADEH F, GOLDFARB D.Second-order cone programming[J]. Mathematical Programming, 2003, 95: 3-51.

[2]LOBO M S, VANDENBERGHE L, BOYD S, et al. Applications of second-order cone programming[J]. Linear Algebra and its Applications,1998, 284: 193-228.

[3]CHI X N, LIU S Y. A one-step smoothing Newton method for second-order cone programming[J]. Journal of Computational and Applied Mathematics, 2009, 223: 114-123.

[4]CHI X N, LIU S Y. A non-interior continuation method for second-order cone programming[J]. Optimization, 2009, 58: 965-979.

[5]FANG L, HE G P, HU Y H. A new smoothing Newton-type method for second-order cone programming problems[J]. Applied Mathematics and Computation, 2009, 215: 1020-1029.

[6]FANG L, FENG Z Z. A smoothing Newton-type method for second-order cone programming problems based on a new smoothing Fischer-Burmeister function[J]. Computational and Appl Mathematics, 2011, 30 :569-88.

[7]TANG J Y, HE G P, DONG L, et al. A smoothing Newton method for second-order cone optimization based on a new smoothing function[J]. Applied Mathematics and Computation, 2011, 218: 1317-1329.

[8]TANG J Y, DONG L, FANG L, et al. Smoothing Newton algorithm for the second-order cone programming with a nonmonotone line search[J]. Optimization Letters, 2014, 8: 1753-771.

[9]TANG J Y, DONG L, FANG L, et al. Analysis of a non-monotone smoothing-type algorithm for the second-order cone programming[J]. Applications of Mathematics, 2015, 60 (1): 35-39.

[10]TANG J Y, HE G P, DONG L, et al. A new non-interior continuation method for second order cone programming[J]. Journal of Numerical Mathematics, 2013, 21 (4): 301-24.

[11]QI L, SUN D, ZHOU G. A new look at smoothing Newton methods for nonlinear complementarity problems and box constrained variational inequalities[J].Mathematical Programming, 2000, 87: 1-35.

(责任编辑朱夜明)

New smoothing Newton algorithm for solving the second-order cone programming

LIU Ruijuan, WU Yejun, ZHANG Yong

(Department of Mathematics and Physics,Nanjing Institute of Technology,Nanjing 210067, China)

In this paper, a new one-step smoothing Newton method was investigated for solving the second-order cone programming(SOCP).It adopted a new smoothing value function and used a Newton equation with disturbance to gain the search direction.Without strict complementarity,it proved that the algorithm was globally and locally quadratically convergent.Finally, numerical experiments demonstrated the feasibility and efficiency of our algorithm.

second-order cone programming;smoothing Newton method;global convergence;quadratucal convergence

10.3969/j.issn.1000-2162.2016.05.002

2016-01-12

国家自然科学基金青年科学基金资助项目(11401301)；南京工程学院校级科研基金资助项目 (QKJA201508)

刘瑞娟(1983-)，女，河南安阳人，南京工程学院讲师.

O231.2

A

1000-2162(2016)05-0008-06