非线性S-G型湿气迁移方程的混合元超收敛分析及外推

罗　娟,毛凤梅,王俊俊

(平顶山学院 数学与信息科学学院, 河南 平顶山　467000)



非线性S-G型湿气迁移方程的混合元超收敛分析及外推

罗娟,毛凤梅,王俊俊

(平顶山学院 数学与信息科学学院, 河南 平顶山467000)

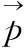
非线性湿气迁移方程; 混合元方法; 超逼近和超收敛; 外推

土壤中的湿气迁移现象可用如下一类非线Sobolev-Galpern型湿气迁移方程来描述

(1)

其中：X=(x,y),Ω⊂R2为边界分段光滑的有界凸多角形区域,a(u)=a(X,t;u),f(u)=f(X,t;u),g(u)=g(X,t;u).方程中的系数a(u),c(t),f(u),e(t),g(u)为已知函数且满足以下假设

(1) 存在正常数a0,a1,c0,c1,f0,f1,e0,e1, 使得对任意X∈Ω,u∈Ω,t∈[0,T]，有a0≤a(u)≤a1,c0≤c(t)≤c1,f0≤f(u)≤f1,e0≤e(t)≤e1;

(2)a(u),f(u),g(u)关于u满Lipschitz连续,且a(u),f(u)关于u具有直到二阶连续有界的导数;

(3) 方程(1)的精确解u∈C2(Ω×[0,T])且存在唯一.

1　有限元的构造及性质

设Ω是一个矩形区域, 其边∂Ω分别平行于x轴和y轴,Γh是Ω满足正则假设的矩形单元剖分族. 设K∈Γh, 平行于x轴和y轴的边分别为l1,l3及l2,l4, 边长分别为2hx,K,2hy,K. 记hK=max{hx,K,hy,K},h=max{hK}(K∈Γh).

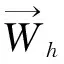
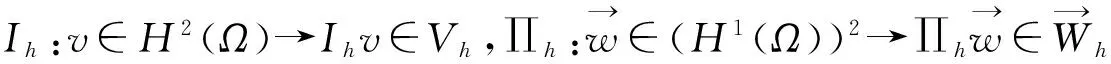
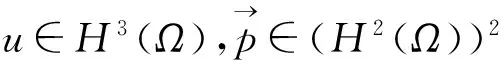
(2)

(3)

(4)

2　半离散格式及超逼近分析

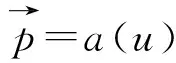
(5)

(6)

(7)

定理1问题 (7) 的解存在唯一.

(8)

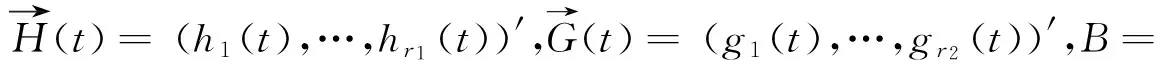
由(8)可得

(9)

(10)

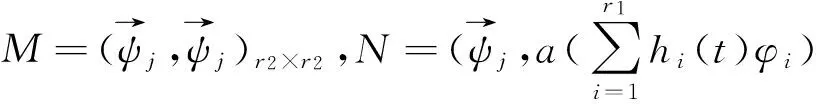
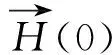
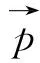
(11)

(12)

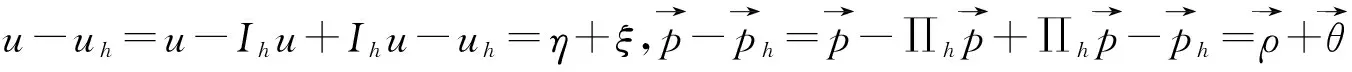
(14)

下面对Ai进行逐项估计.由f(u)、e(t)、c(t)有界及由Schwartz不等式、插值理论和Young不等式, 分别得到|A1+A2|≤ε‖‖(‖‖‖‖.

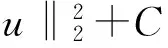
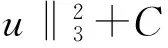
(15)

当ξ(X,0)=0时,有

(16)

将(16)式代入(15)式, 得

(17)

由Gronwall引理, 得

(18)

(19)

综上可得

(20)

由(11),(18)和(20)式知(12)式成立. 定理证毕.

定理3在定理2的条件下, 有如下整体超收敛结果

(21)

(22)

3　外　推

引理2[12]设u∈H3(Ω),∀vh∈Vh,则有

(23)

进一步, 若u∈H4(Ω),∀vh∈Vh,则有

(24)

引理3[13]设u∈H4(Ω),∀vh∈Vh,则有

(25)

(26)

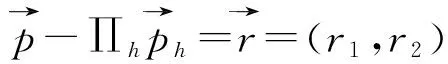
得

(27)

(28)

(29)

其中

类似于前面的方法,对上面的每一项进行估计,得

(30)

(31)

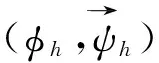
(33)

(34)

(35)

由(27), (34)式和(35)式知(28)式成立. 定理证毕.

为了给出外推解,可以类似于文[10]中的思想, 构造插值算子I3h,∏3h, 于是有以下外推的结果：

(36)

注2上述外推解与文[8]研究的线性问题的结果一样, 但总体自由度却减少2NP.

[1]AIFANTIS E C. On the problem of diffusion in silids[J]. Acta Mechanica, 1980, 37 (2): 265-296.

[2]施德明. 非线性湿气迁移方程的初边值问题[J]. 应用数学学报, 1990, 13 (1): 31-38.

[3]周家全, 许超, 裴丽芳, 等. 一类非线性Sobolev-Galpern型湿气迁移方程的质量集中非协调有限元方法[J]. 生物数学学报, 2013, 28 (2): 324-330.

[4]陈绍春, 陈红如. 二阶椭圆问题新的混合元格式[J]. 计算数学, 2010, 32 (2): 213-218.

[5]史峰, 于佳平, 李开泰. 椭圆型方程的一种新型混合有限元格式[J]. 工程数学学报, 2011, 28 (2): 231-237.

[6]石东洋, 李明浩. 二阶椭圆问题一种新格式的高精度分析[J]. 应用数学学报, 2014, 37 (1): 45-58.

[7]张亚东, 石东洋. 各向异性网格下抛物方程一个新的非协调混合元收敛性分析[J]. 计算数学, 2013, 35 (2): 171-180.

[8]石东洋, 张亚东. 抛物型方程一个新的非协调混合元超收敛分析及外推[J]. 计算数学, 2013, 35 (4): 337-352.

[9]史艳华, 石东洋. Sobolev方程新混合元方法的高精度分析[J]. 系统科学与数学, 2014, 34 (4): 452-463.

[10]林群, 严宁宁. 高校有限元构造与分析[M]. 保定: 河北大学出版社, 1996.

[11]HALE J K. Ordinary differential equations[M]. New York: Willey-Interscience, 1969.

[12]LIN Q, LIN J F. Finite element methods: accuracy and improvement[M]. Beijing: Science Press, 2006.

[13]史艳华, 石东洋. 非对称不定问题双线性元的超收敛和外推[J]. 应用数学, 2013, 26 (1): 220-227.

(责任编辑朱夜明)

Superconvergence analysis and extrapolation of mixed finite element approximation for nonlinear S-G type equations of moisture migration

LUO Juan, MAO Fengmei, WANG Junjun

(School of Mathematics and Information Science, Pingdingshan University, Pingdingshan 467000,China)

nonlinear moisture migration equation; mixed finite element method; superclose properties and superconvergence; extrapolation

10.3969/j.issn.1000-2162.2016.05.004

2016-01-17

国家自然科学基金资助项目(11271340)

罗娟(1980-),女, 河南南阳人, 平顶山学院讲师.

O242

A

1000-2162(2016)05-0018-06