一种帕金森患者行走步态的非线性特征分析
2016-09-21许胜强杨先军
王 振,程 楠,陈 炜,许胜强,杨先军*
(1.安徽大学 电子信息工程学院,安徽 合肥 230601;2.中国科学院 合肥智能机械研究所,安徽 合肥 230031;3.安徽中医药大学 神经病学研究所附属医院,安徽 合肥 230061;4.安徽省体育局 体育科学技术研究所,安徽 合肥 230001)
一种帕金森患者行走步态的非线性特征分析
王振1,2,程楠2,3,陈炜4,许胜强2,杨先军2*
(1.安徽大学 电子信息工程学院,安徽 合肥 230601;2.中国科学院 合肥智能机械研究所,安徽 合肥 230031;3.安徽中医药大学 神经病学研究所附属医院,安徽 合肥 230061;4.安徽省体育局 体育科学技术研究所,安徽 合肥 230001)
鉴于医师对帕金森患者病情严重程度的诊断存在一定的主观性,使其无法对患者进行更加有效的治疗,提出一种基于帕金森患者行走步态的非线性特征的客观定量分析方法.利用去趋势波动分析法和重复周期密度熵,对正常青年人、正常老年人以及老年帕金森患者的行走步态信号中的地面反作用力信息进行定量非线性分析,然后将所提方法的参数与传统时域参数进行相关性对比分析.实验结果表明:帕金森患者与正常人相比较,二者的步态信号在稳定性、长程相关性和重复周期性方面均有显著差别.研究结果能为帕金森患者病情的分级评估以及诊断康复,提供一种简单有效的指导方法.
地面反作用力;去趋势波动分析;标度指数;重复周期密度熵;相关性系数
帕金森病(Parkinson’s disease,简称PD)是一种多发于中老年人群神经系统的变性疾病,主要症状有静止性震颤、肌僵直、运动迟缓和步态障碍[1],其中步态障碍表现为下肢活动幅度降低、小碎步、转弯困难和步态冻结[2],这些症状严重影响了帕金森患者的正常生活.然而帕金森病的发病机制尚未完全研究清楚,医师对帕金森病患者的诊断存在一定的主观性,从而无法对患者的病情进行有效的评估和治疗,因此有必要引入一种客观的测量方法,能够定量评估患者的病情和康复情况.
步态是人类在运动过程中表现出的一种行为特征,通过生物力学手段对步态信息的采集研究能揭示出一些行为的异常本质[3],进而将其运用到医学的治疗与诊断中.3维测力台作为一种步态采集装置能够测量足底受到的3维地面反作用力信息,已在步态识别和医疗诊断领域得到应用,而步态信号分析方法多为传统的时域和频域分析[4-9],且未将步态中的3维力信息应用到帕金森病的研究中.相对传统的步态信号时频分析,笔者拟将去趋势波动分析 (detrended fluctuation analysis,简称DFA) 和重复周期密度熵(recurrence period density entropy,简称RPDE)相结合,应用到医学步态信号分析中,对3维地面反作用力中垂直方向上的力进行非线性分析,将其与传统时域参数进行相关性对比分析.
1 帕金森患者行走步态的非线性特征
1.1DFA
Peng等[10]提出的去趋势波动分析中,将标度指数(scaling exponent,简称α)用于检测一段信号的长程相关性,通过对信号累积和的分段去趋势运算,来突出信号中的弱相关成分.去趋势可有效消除信号中的测量噪声,从而得出信号内在的波动和相关性.经过多年的发展,DFA方法不仅在经济学、气象学、地理学、机械学等领域有广泛应用[11-15],而且在生物医学信号的分析研究中也发挥了重要作用,如语音信号、心电信号和脑电信号等.
DFA方法的步骤如下:
(1) 对于长度为N的时间序列x(i) (i=1,2,3,…,N),计算如下的累积时间序列
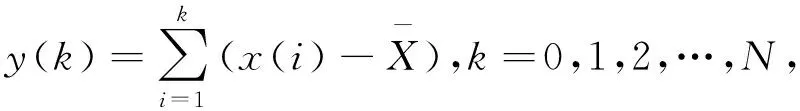
(1)
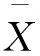
(2) 将得到的累积时间序列均匀划分为等长度的子段,每段的长度为s(尺度),共有M=int(N/s)个子段.由于N可能不被子段的长度整除,为了保留时间序列末端的信息,从原序列末端向前再划分一次,共得到2M个子段.
(3) 对每一个子段进行多项式拟合,设拟合的阶数为p,每个子段数据的p阶局部趋势为ps(i),将累积时间序列y(i)减去该局部趋势后,得到去趋势序列为
(2)
(4) 计算如下波动函数
(3)
(5) 以固定的间隔来变换尺度s的大小,重复上述计算步骤获取波动函数和尺度之间的关系.
通常情况下波动函数Fs和尺度s之间存在幂律关系,即Fs∝sα.对波动函数Fs与尺度s作双对数图,然后利用最小二乘法对图中的点进行拟合,所得到直线的斜率即为标度指数α.标度指数α值的不同范围反应信号的不同特性:若0<α< 0.5,则信号的长程相关性具有反持续性(anti-persistent);若α= 0.5,则信号为白噪声,无相关性;若0.5<α<1,则信号的长程相关性具有持续性(persistent);若α=1,则信号为1/f噪声;若α>1,则信号存在强的长程相关性;若α=1.5,则信号为布朗噪声.
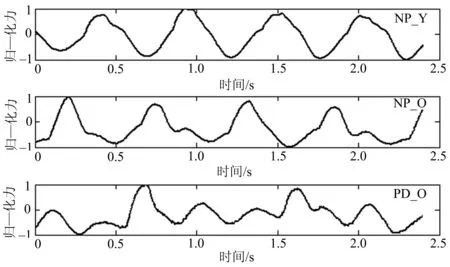
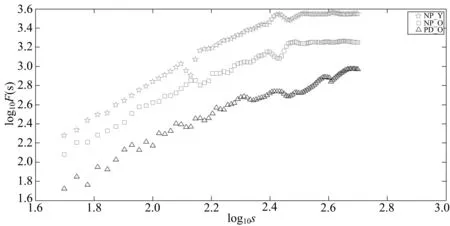
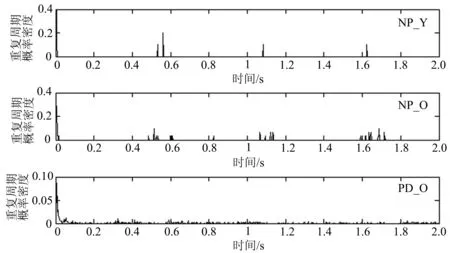
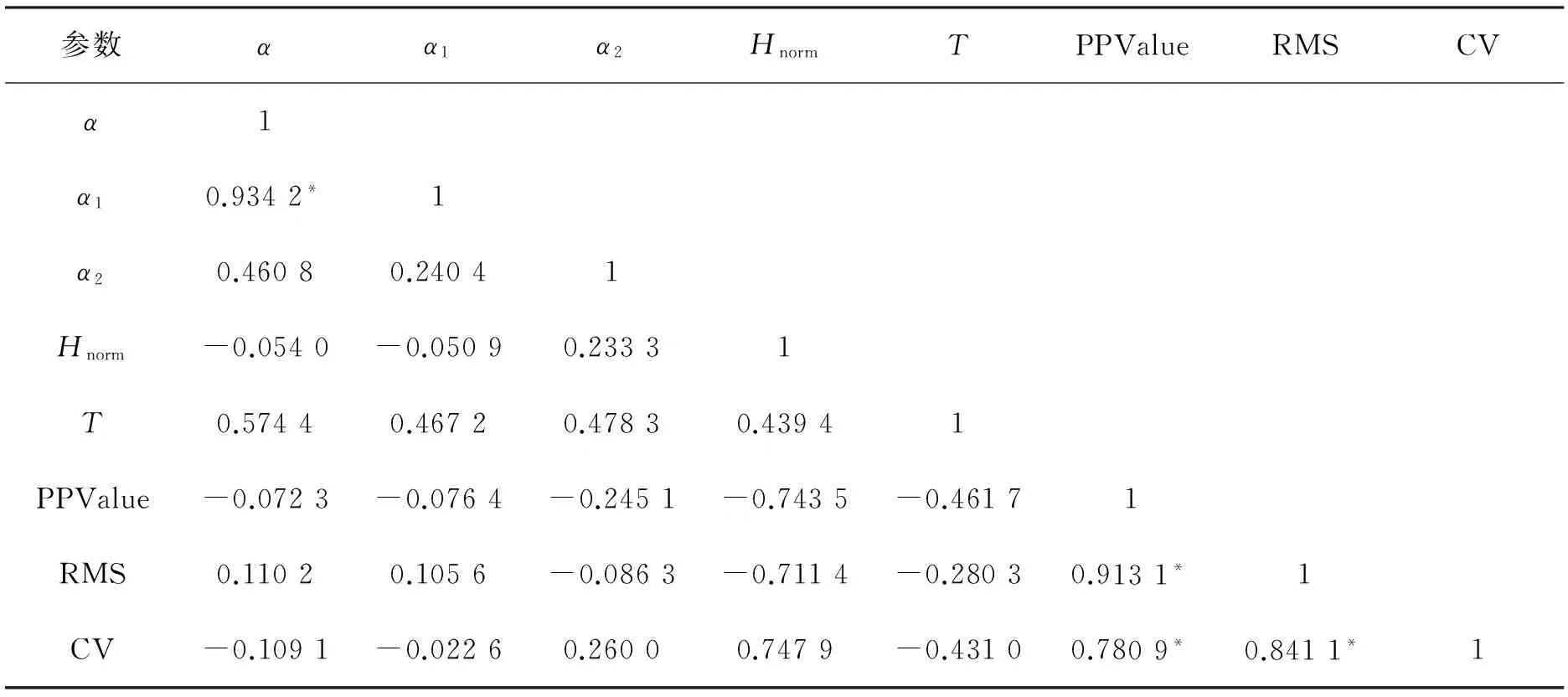
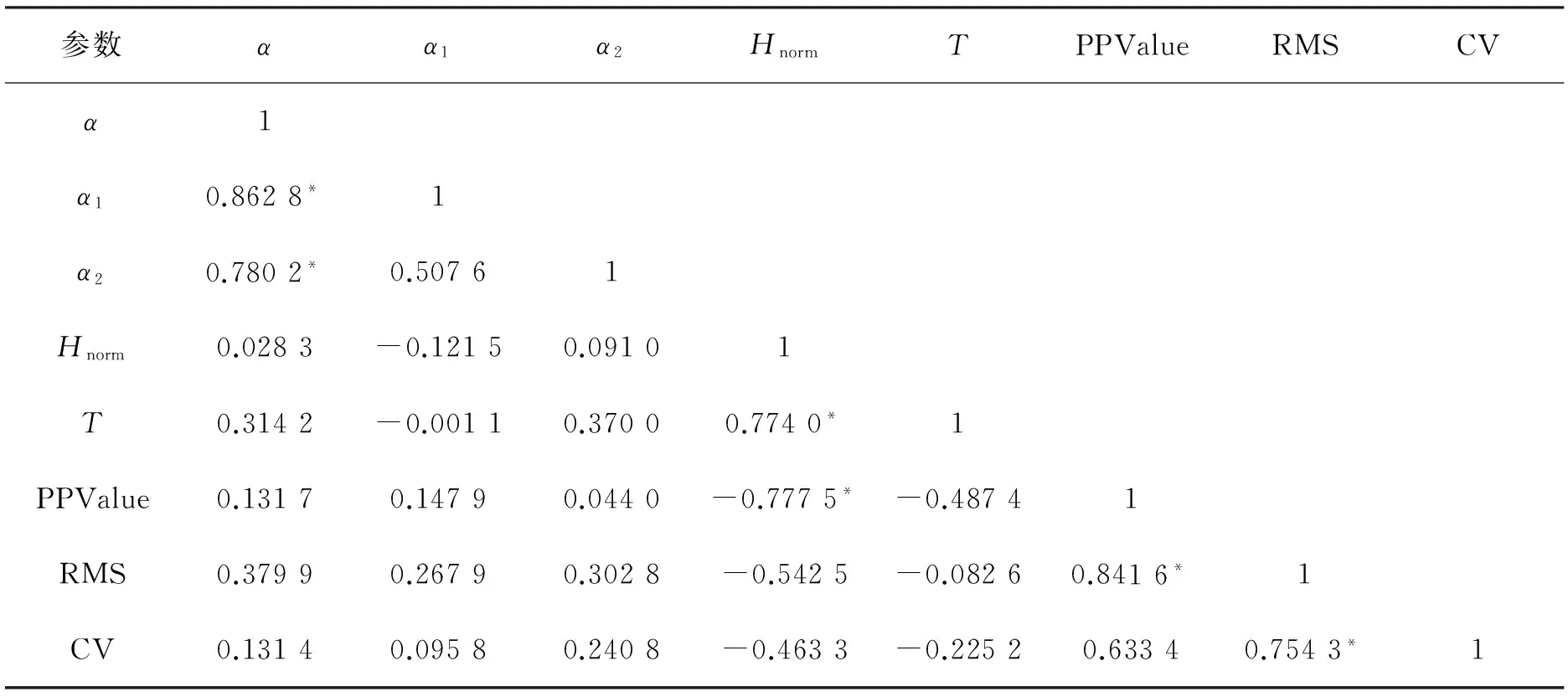
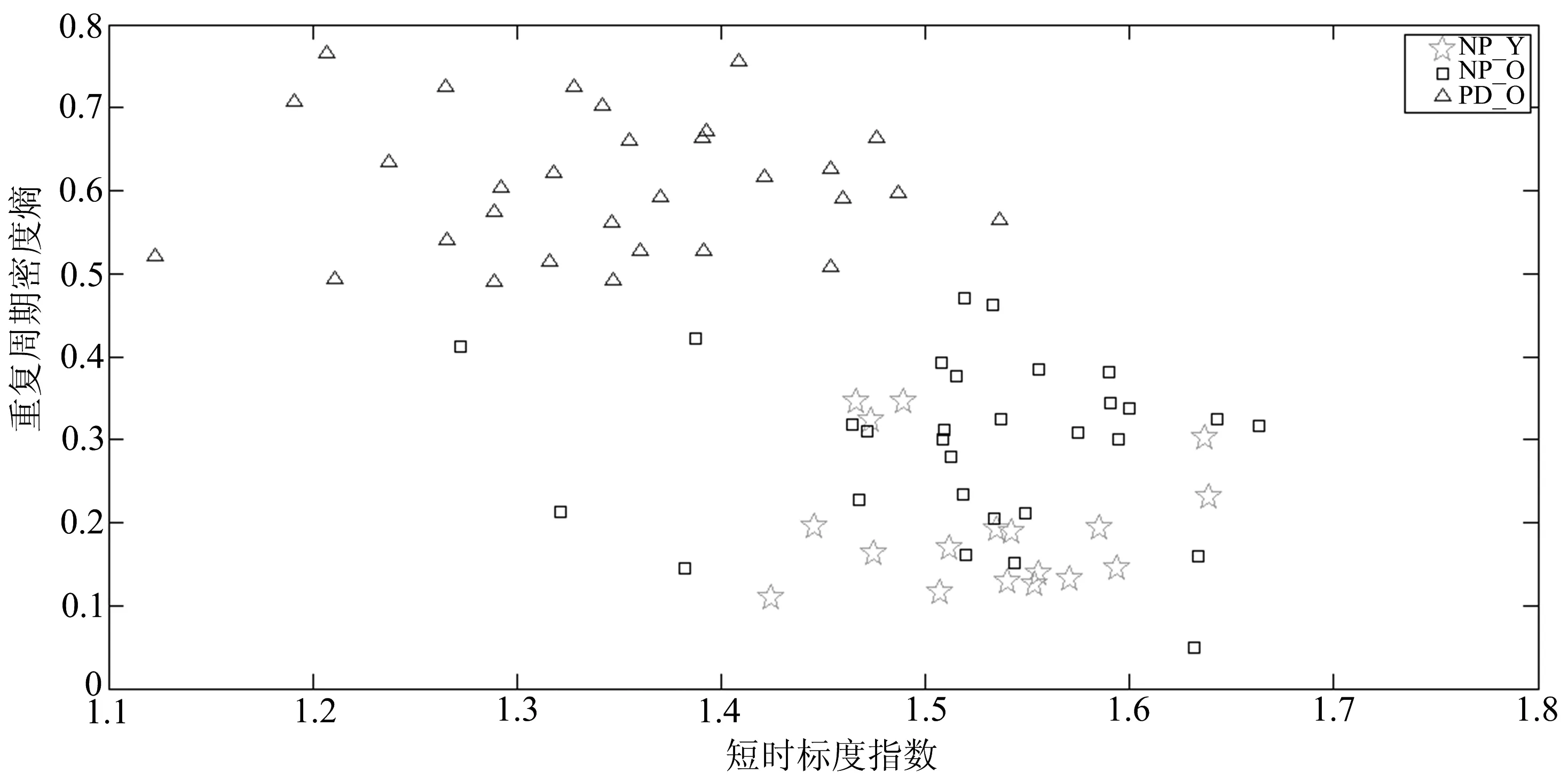
去趋势波动分析中,尺度s的选择对最终的标度指数有重要的影响.尺度s选择过大或者过小都会产生不同大小的标度指数,从而影响信号的准确性.如果尺度间隔等于2,进行一阶线性拟合时去趋势序列等于零,所以尺度取值范围应限制在3与序列长度N之间.一般来说,s的取值范围为[q+2,N/4],q为所选择的拟合阶数,N为时间序列长度[16-18].尺度间隔的大小对计算结果有影响,间隔太小会增加计算的复杂度,太大会无法得到可靠的统计特性.基于上述分析,笔者选择的尺度范围为50~500,尺度间隔为5.DFA标度指数的双对数图中,一般会产生两条直线交叉(crossover)[14]的情况,所以对信号提取了短时标度指数α1(50 1.2RPDE RPDE能反映一段信号的周期性或者重复性程度,主要用于非线性动力学和随机信号分析[11].类似于定量递归分析,RPDE的基础是对原始信号进行相空间重构.根据Takens的延迟嵌入定理[19-20],对于原始时间序列x(i) (i=1,2,…),选择适当的延迟t,构造的m维向量如下 (4) 构造的m维相空间中,每一个m维向量相当于一个点,以X(0)为球心构造一个m维半径为r的球体,则相空间中的轨迹点X(1),X(2),…依次向前推进直到离开半径为r的球体表面,此时 ||X(0)-X(i)||>r(欧式距离).假设当第一次回到球内的轨迹点为X(n1),即||X(0)-X(n1) ||≤r,记录轨迹点离开球体表面和回到球内的时间,并存储到递归时间函数R(i)中.将所有的轨迹点重复递归下去,形成一个重复递归的时间直方图.规范化后的重复周期的概率密度为 (5) 其中:Tmax为重复周期中的最大时间.P(T)对应的香农信息熵为 (6) 将香农信息熵H归一化,且控制其取值范围在[0,1]之间,可得重复周期密度熵为 (7) 行走过程中人的步态是一种非平稳信号,因此可采用重复周期密度熵来分析步态信号.与重复周期密度熵相关的参数,笔者选取如下:嵌入维数m=3,时间延迟t=7,半径r=0.12,Tmax=1 000. 1.3传统时域参数和相关性系数 为了更加深入了解帕金森患者与正常人群之间行走步态的差别,笔者提取了步态信号中的一些传统时域特征参数,如走完步态通道所需总时间T、峰峰值PPValue、均方根RMS和变异系数CV.相对于非线性分析,传统时域参数更能简单直观反应行走过程步态的速度和稳定性. 为了说明帕金森患者与健康者之间的步态参数的区别,在正常组和患者组之间分别对传统时域参数、标度指数和重复周期密度熵值进行了t检验.相关性系数(correlationcoefficient)是反应变量之间线性相关程度的一种统计指标.为了对比非线性特征参数与传统时域参数的相关性,笔者计算了所有特征参数之间的相关性矩阵,以检验非线性特征的有效性. 2.1实验对象 实验中选取78个样本进行3维测力台通道(采样频率为500Hz)行走实验,78个样本分别为:18名正常青年人(年龄(24±3)岁,体重(60±10)kg),30名正常老年人(年龄(59±8)岁,体重(62±14)kg)以及30名老年PD患者(年龄(64±10)岁,体重(61.2±10)kg),其中PD患者的病情已由医师确诊为Hoehn&Yahr分级中的Ⅰ~Ⅲ期.以NP_Y(normalperson_young)表示正常青年组,以NP_O(normalperson_old)表示正常老年组,以PD_O(Parkinson’sdisease_old)表示老年PD患者组.实验前让测试对象对测力台通道的环境有充分了解和适应,以保证数据采集的可靠性.让每个人以正常自然的姿态方式在测力台通道上行走3次,每次间隔1min.若PD患者每次走完后感觉身体疲劳或不适,需适当休息后再进行下次实验.图1为从3组人群中各选出一个样本的垂直方向力的一段原始信号,为了方便对比,只截取了一段长度,并归一化到了-1~1之间. 图1 垂直方向力的一段原始信号Fig.1 An original signal of vertical force 2.2DFA 由于行走过程中垂直方向反作用力的特征最为明显,所以选取垂直方向反作用力fz来进行去趋势波动分析,统计了3组样本的标度指数的平均值和标准差,结果如表1所示. 表1 标度指数的平均值和标准差 注:*表示0.01 从表1可知,3组数据的全程标度指数α相差不大,正常组略大于PD患者组;NP_Y和NP_O的短时标度指数α1分别都达到了1.53和1.52,明显大于PD_O的平均值1.34;PD_O的长时标度指数α2平均值为0.38,明显大于正常对照组NP_O的,略大于NP_Y的,但是PD_O的指数值波动性最大.除了NP_Y的α值与PD_O的差异较小外,其他的都与患者组有明显的差异.图2为选取的3组样本信号去趋势分析的双对数图.从图2可知,随着尺度的增加,3组曲线都变得越来越平滑,趋势变得更加缓慢,但是正常组的曲线较患者组的整体要规则些,并且明显处于患者组的上方. 图2 3组样本信号去趋势分析的双对数图Fig.2 Fractal scaling exponent on log-log plot of the three groups of sample signal 去趋势波动分析所求得的标度指数反映了信号内部的一种固有的自相似性特征,能够有效地消除时间序列中的非平稳性所导致的虚假长程相关性,从而可揭示出信号本身所隐藏的内在相关性.从计算结果中可以看出,正常对照组的标度指数都高于PD患者组,说明健康人群行走过程中步态信号的长程相关性要比患者的更加稳定. 从全程标度指数α的结果来看,NP_Y和NP_O之间相差不大.而从短时标度指数α1来看,它们之间的关系为α1NP_Y>α1NP_O>α1PD_O,说明正常年轻人的行走步态最为稳定,有较高的持续性,而由于年龄和疾病因素的影响,NP_O和PD_O行走过程中的步态越来越趋于不稳定,严重时PD_O甚至还会出现步态冻结现象.3组样本长时标度指数都是小于0.5,长时标度指数的平均值之间的关系为α2NP_Y<α2NP_O<α2PD_O.3组样本的标准差都接近平均值,而PD_O组的标准差最大,说明PD患者行走步态中长程相关的反持续性存在不稳定的情况. 2.3RPDE 同样选取垂直方向的反作用力fz来进行重复周期密度熵的计算,统计了3组样本的重复周期密度熵的平均值和标准差,结果如表2所示. 表2 重复周期密度熵的平均值和标准差 注:**表示P<0.01. 由表2可以看出,PD_O的重复周期密度熵明显高于正常对照组,其平均值达到了0.59,NP_O的稍大于NP_Y的,3组数据的波动性差别不大.图3为3组样本信号的重复周期概率密度与时间的关系曲线.从图3可以看出,3类样本的关系曲线具有明显差异. 图3 重复周期概率密度与时间的关系曲线Fig.3 The relationship curve between recurrence period probability density and time 2.4传统时域参数和相关性系数 同样选取垂直方向的反作用力fz来进行传统时域参数的计算,统计了3组样本的传统时域参数的平均值和标准差,结果如表3所示. 表3 传统时域参数的平均值和标准差 注:*表示0.01 从表3可以看出,对于参数T的平均值有TNP_Y 分别对不同组别的标度指数(α,α1,α2)、重复周期密度熵值(Hnorm)和传统时域参数进行相关性检验,结果分别如表4~6所示.由表4~6可以发现,3组样本的标度指数与传统时域参数的相关性均不强,重复周期密度熵与传统时域参数均有一定的相关性,标度指数与重复周期密度熵的相关性均不强. 表4 NP_Y的参数相关性 注:*表示0.01 表5 NP_O的参数相关性 注:*表示0.01 表6 PD_O的参数相关性 注:*表示0.01 计算非线性特征参数、传统时域特征参数及其内部各参数之间的相关性,有助于发现信号中的一些相似性特征,从而对信号可以进行更加有效的分析.从表4~6中可以看出,3组样本的相关性整体趋势大致相同.去趋势分析中的标度指数除了α与α1之间的相关性较高外,与其他的参数之间的相关性都很低(故标度指数能够作为一种新的特征来反映帕金森患者的步态状况),而重复周期密度熵值Hnorm与一些时域参数之间相关性较高.从相关性系数表中挑选了非线性特征中相关性较低的α1和Hnorm,分别对3组样本做出的散点分布如图4所示,从图4中发现帕金森患者和正常人群之间的分布具有明显的离散性. 图4 基于短时标度指数α1和重复周期密度熵Hnorm的散点分布Fig.4 Scatter plot based on short-term scaling exponent α1 and recurrence period density entropy Hnorm 笔者利用去趋势波动分析和重复周期密度熵对正常青年、正常老年和老年帕金森患者3类人群行走步态中垂直方向上的地面反作用力进行了非线性分析. 去趋势波动分析能够通过去除趋势,消除信号表面存在的虚假相关性,探测出信号的内在相关规律,而重复周期密度熵则量化了信号的重复周期性.相对传统的时域分析,这两种方法能够更加简单有效地对非平稳的行走步态信号做出定量分析.分析结果发现3组人群的步态信号具有显著的差别,随着年龄的增长和疾病因素,行走中的步态信号的长程相关性和周期重复性都会降低.对步态信号的标度指数、重复周期密度熵及一些传统的时域参数作了相关性对比分析,发现标度指数与传统时域参数的相关性较低,而重复周期密度熵与传统时域参数的相关性较高,标度指数与重复周期密度熵的相关性较低.标度指数和重复周期密度熵可以作为正常组与帕金森患者组之间聚类分析的特征,以及帕金森患者的病情评估和诊断的定量指标. [1]蒋思明, 张克忠. 帕金森病冻结步态的研究进展[J]. 中国临床神经科学, 2015, 2: 199-204. [2]李利, 刘晶, 章文斌, 等. 帕金森病冻结步态治疗进展[J]. 临床神经外科杂志, 2014, 4: 318-320. [3]吴剑, 李建设. 人体行走时步态的生物力学研究进展[J]. 中国运动医学杂志, 2002, 3: 305-307. [4]林尔东, 姚志明, 郑重, 等. 一种改进的基于地面反作用力的步态识别方法[J]. 模式识别与人工智能, 2011, 3: 353-359. [5]陆葵, 杨庆铭. 三维测力台在股骨头坏死患者步态分析中的应用[J]. 上海第二医科大学学报, 1996, 6: 445-447. [6]李爱萍, 胡军, 刘合荣. 基于三维测力台系统的人体步态分析[J]. 微计算机信息, 2010, 13: 226-228. [7]刘政. 基于三维足底压力检测的人体防摔策略研究[D]. 长春: 吉林大学机械科学与工程学院, 2014. [8]孟庆华, 鲍春雨, 陈超, 等. 男性青年踝关节外侧副韧带损伤后行走步态分析[J]. 医用生物力学, 2014, 4: 65-71. [9]耿楠, 于天源, 刘卉, 等. 颈椎定位旋转扳法操作特征的运动生物力学参数分析[J]. 长春中医药大学学报, 2015, 3: 607-610. [10]PENG C K, BULDYREV S V, HAVLIN S, et al. Mosaic organization of DNA nucleotides[J]. Phys Rev E, 1994, 49 (2): 1685-1689. [11]LITTLE M A, MCSHARRY P E, ROBERTS S J, et al. Exploiting nonlinear recurrence and fractal scaling properties for voice disorder detection[J]. Biomedical Engineering Online, 2007, 23 (3): 23-58. [12]RIZVI S A R, DEWANDARU G, BACHA O I, et al. An analysis of stock market efficiency: developed vs Islamic stock markets using MF-DFA[J]. Physica A Statistical Mechanics & its Applications, 2014, 407: 86-99. [13]IVANOVA K, AUSLOOS M. Application of the detrended fluctuation analysis (DFA) method for describing cloud breaking[J]. Physica A Statistical Mechanics & its Applications, 1999, 274 (1): 349-354. [14]PENG C K, HAVLIN S, STANLEY HE, et al. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series[J]. Chaos(an Interdisciplinary Journal of Nonlinear Science), 1995, 5 (1): 82-87. [15]林近山, 陈前. 基于多重分形去趋势波动分析的齿轮箱故障特征提取方法[J]. 振动与冲击, 2013, 32 (2): 97-101. [16]KANTELHARDT J W, KOSCIELNY-BUNDE E, REGO H H A, et al. Detecting long-range correlations with detrended fluctuation analysis[J]. Physica A Statistical Mechanics & its Applications, 2001, 295 (3): 441-454. [17]侯威, 章大全, 杨萍, 等. 去趋势波动分析方法中不重叠等长度子区间长度的确定[J]. 物理学报, 2010, 59 (12): 8986-8993. [18]李力, 彭中笑, 彭书志. 去趋势波动分析在齿轮故障诊断中的应用研究[J]. 中国机械工程, 2009 (19): 2311-2314. [19]KANTZ H, SCHREIBER T. Nonlinear time series analysis[M]. New York: Cambridge University Press, 1999. [20]TAKENS F. Detecting strange attractors in turbulence[J]. Lecture Notes in Mathematicks, 1981, 898: 366-381. (责任编辑郑小虎) A kind of nonlinear gait characteristic analysis in patients with Parkinson’s disease WANG Zhen1,2, CHENG Nan2,3, CHEN Wei4, XU Shengqiang2, YANG Xianjun2* (1.School of Electronics and Information Engineering, Anhui University, Hefei 230601, China;2. Institute of Intelligent Machines, Chinese Academy of Sciences, Hefei 230031, China;3. Affiliated Hospital of Neurological Institute, Anhui University of Traditional Chinese Medicine, Hefei 230061, China;4. Sports Science and Technology Research Institute, Anhui Province Sports Bureau, Hefei 230001, China) In view of the subjectivity of the physician’s diagnosis of Parkinson’s patients with different conditions, we proposed an objective quantitative analysis method of nonlinear characteristics based on gait signal in Parkinson’s patients. Firstly, two nonlinear quantitative analysis methods, detrended fluctuation analysis and recurrence period density entropy, were used to analyze the ground reaction force gait signal of healthy young people, healthy old people and elderly Parkinson’s patients. Then the characteristics of proposed methods and some of the classical time-domain characteristics were compared by statistical correlation analysis. The experiment results showed that gait signal between Parkinson’s patients and the normal person had significant differences in stability, long-range correlation and periodicity. It indicated that this study provided a simple and effective method for classification evaluation, diagnosis and rehabilitation of Parkinson’s disease. ground reaction force; detrended fluctuation analysis; fractal scaling exponent; recurrence period density entropy; correlation coefficient 10.3969/j.issn.1000-2162.2016.05.011 2016-02-17 安徽省科技攻关计划项目(1301042215,1501021042);国家科技支撑计划项目(2013BAH14F01) 王振(1990-),男,安徽合肥人,安徽大学硕士研究生;*杨先军(通信作者),中国科学院合肥智能机械研究所副研究员,硕士生导师,E-mail: xjyang@iim.ac.cn. O156 A 1000-2162(2016)05-0065-08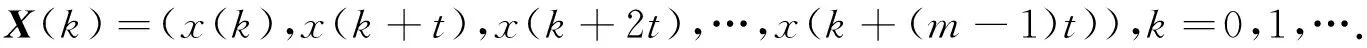
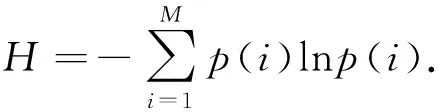
2 实验与分析




3 结束语
