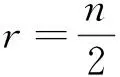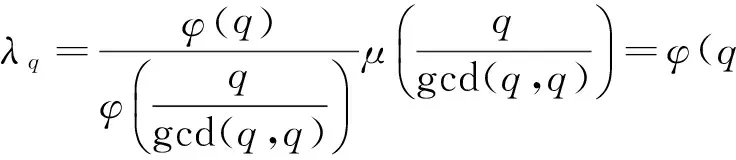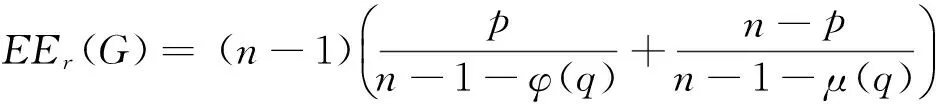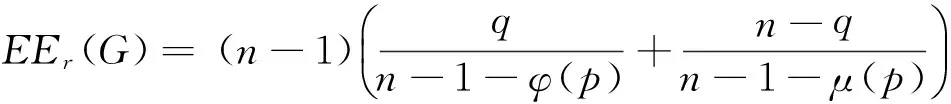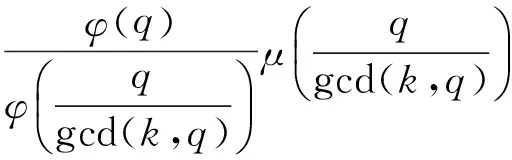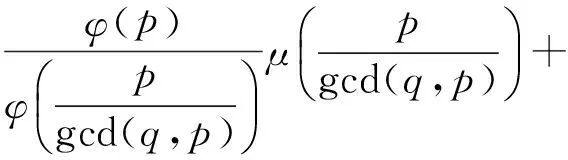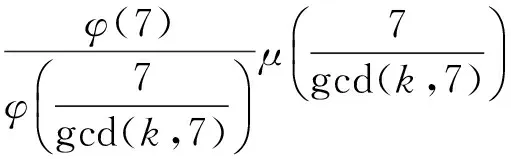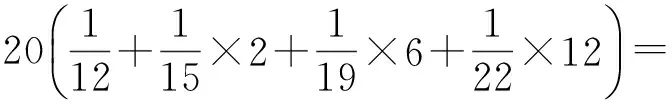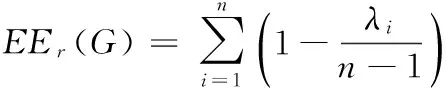循环图的预解Estrada指标
2016-09-16周后卿
周 后 卿
(邵阳学院 数学系, 湖南 邵阳 422000)
循环图的预解Estrada指标
周 后 卿
(邵阳学院 数学系, 湖南 邵阳 422000)

循环图;整循环图;预解Estrada指标;特征值
Journal of Zhejiang University(Science Edition), 2016,43(5):517-520
0 引 言
设G是一个具有n个顶点的简单图,G的邻接矩阵记为A(G).设A(G)的特征值为λ1,λ2,…,λn. 定义G的预解Estrada指标(以下用EEr(G) 表示)为

图的预解Estrada指标在测量复杂网络中心度时具有重要作用,许多学者对其进行了研究.CHEN等[1]讨论了EEr(G)的下界问题,得到:

文献[2]推出了一个计算预解Estrada指标的公式:
对任何一个具有n个顶点的非完全图G,其预解Estrada指标为
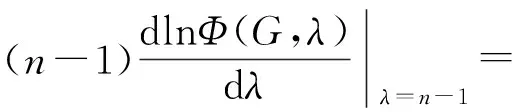

其中Φ(G,λ)为G的特征多项式.
文献[2]还证明了,若图G去掉一条边e后,其预解Estrada指标就会下降,即
EEr(G-e) 从而得到完全图的预解Estrada指标最大. 文献[3]也讨论了具有最小预解Estrada指标的极图问题,得到如下结果: 在具有n(n≥1)个顶点的所有连通图中,路图的预解Estrada指标最小. 本文主要研究循环图、整循环图的预解Estrada指标问题. 若一个图是循环群上的Cayley图,其邻接矩阵是一个循环矩阵,则称其为循环图.具有n个顶点的循环图记为G(n,S),S⊆{0,1,2,…,n-1},0∉S,集合S为循环图G(n,S)的符号集.它是这样一个集合:若其任意2个顶点i与j相邻,当且仅当i-j(modn)∈S,n为正整数,S=-S.一个图若其邻接矩阵的特征值都为整数,则称其为整谱图.特征值全为整数的循环图称为整循环图.为便于表述,习惯将整循环图记为ICGn(D).在过去的几十年里,循环图已广泛应用于编码理论、VLSI设计、Ramsey理论、并行计算和分布式计算,在量子物理学中也有应用,并发挥了重要作用. 循环图具有重要的互联网络拓扑结构,同步性与稳定性很好,是点可迁图.设循环图G(n,S)的邻接矩阵为 由文献[5]可知,循环图G(n,S)的特征值为 即 λr=a0+a1ωr+a2ω2r+…+an-1ω(n-1)r. 设S={l1,l2,…,lk}(l1 λr=ωl1r+ωl2r+…+ωlkr= 0≤r≤n-1. (1) 并非所有的循环图都是整循环图.那么, 成为整循环图应该具备什么条件? Dn={d1,d2,…,dk},di|n, 文献[4]证明了 对于Ramanujan和,通常用 表示.这里,φ(x)表示Euler函数,即 其中p1,p2,…,pn是x的素因数,φ(1)=1. μ(x)表示Mobius函数,即 μ(x)= KLOTZ等[6]证明了整循环图ICGn(D)的特征值为 注意到,对n的任何因数d,下列等式成立: (2) 对于循环图,本文只讨论度为偶数的循环图的预解Estrada指标.首先有下列定理. 则G(n,S)的预解Estrada指标满足下列不等式: 证明根据式(1), 不妨设λ0最大,显然,λ0=2k.又由于 λ0+λ1+…+λn-1=0, 所以 λ1+λ2+…+λn-1=-2k, 则 2[(-1)l1+(-1)l2+…+(-1)lk]. 对于整循环图,研究n能够分解为2个互素因子的情况.下面就S的几种不同情形予以讨论,得到下列结论. 定理2若n=pq,2 证明取D={p}⊂{1,p,q}=Dn, Gn(p)={p,2p,…,(q-1)p}, 于是,推出整循环图G(n,S)的特征值 类似地,可得到: 定理4若n=pq,2 证明令D={p,q}⊂{1,p,q}=Dn,则 Gn(p)={p,2p,…,(q-1)p},Gn(q)={q,2q, S={p,2p,…,(q-1)p,q,2q,…,(p-1)q}. 利用式(2),推出整循环图的G(n,S)特征值为 可求得 μ(p)+μ(q), φ(p)+μ(q), μ(p)+φ(q), φ(p)+φ(q). 于是,得到整循环图G(n,S)的特征值 从而,解得G(n,S)的预解Estrada指标 例1取n=21,令D={3,7}⊂{1,3,7}=D21,则 G21(3)={3,6,9,12,15,18},G21(7)={7,14}, 因而S=G21(3)∪G21(7)={3,6,7,9,12,14,15,18}.则G(n,S)=G(21,S)是一个整循环图.由式(2),可得到特征值 从而求得整循环图G(21,S)的图谱为 Spec(G(21,S))={8,5(2),1(6),-2(12)}.于是,可推得整循环图G(21,S)的预解Estrada指标 21.54. 本文只讨论了度为偶数时循环图的预解Estrada指标情况.度为奇数时的情况,有待下一步研究. 审稿专家提出了有益的修改建议,特此致谢! [1]CHENXiaodan,QIANJianguo.BoundingtheresolventEstradaindexofagraph[J]. Journal of Mathematical Study,2012(2):159-166. [2]CHEN Xiaodan, QIAN Jianguo. On resolvent Estrada index[J]. Match Commun Math Comput Chem,2015,73:163-174. [3]IVAN G, BORIS F, CHEN X. Graphs with smallest resolvent Estrada indices[J]. Match Commun Math Comput Chem,2015,73:267-270. [4]SO W. Integral circulant graphs[J]. Discrete Mathematics,2006,306:153-158. [5]DAVIS P J. Circulant Matrices[M]. New York: John Wiley & Sons,1979. [6]KLOTZ W, SANDER T. Some properties of unitary Cayley graphs[J]. The Electronic Journal Combinatorics,2007,14(1):697-714. Resolvent Estrada index for circulant graphs. ZHOU Houqing (DepartmentofMathematics,ShaoyangUniversity,Shaoyang422000,HunanProvince,China) circulant graph; integral circulant graph; resolvent Estrada index; eigenvalue 2015-12-22. 湖南省教育厅科学研究项目(15C1235);邵阳市科技局科技计划项目(2015JH41). 周后卿(1963-),ORCID:http://orcid.org/0000-0002-9813-1687,男,硕士,教授,主要从事组合数学研究,E-mail:zhouhq2004@163.com. 10.3785/j.issn.1008-9497.2016.05.003 O 157.5 A 1008-9497(2016)05-517-041 有关循环图的背景知识




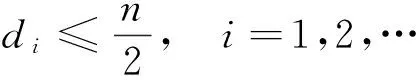

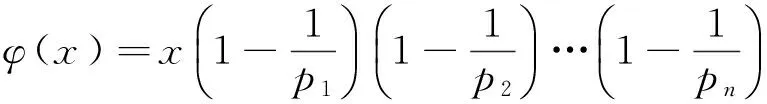
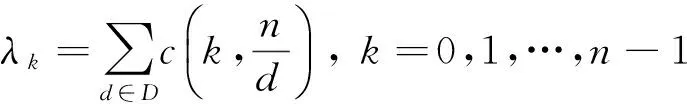

2 主要结论