双曲空间中全脐超曲面与高斯映照像

2016-09-16王琪

浙江大学学报（理学版） 2016年5期

关键词：黎曼双曲曲率

王　琪

(贵阳学院数学与信息科学学院，贵州贵阳 550005)

双曲空间中全脐超曲面与高斯映照像

王琪

(贵阳学院数学与信息科学学院，贵州贵阳 550005)

设Mn是单位双曲空间形式Hn+1中定向的紧致无边超曲面.假设存在整数r(1≤r≤n-1)使得高阶平均曲率Hi>0,i=1,2,…,r,且Hr是常数.证明了：如果Mn的高斯映照像包含在一个开半球面内,则Mn全脐.

单位双曲空间形式；全脐超曲面；高斯映照像；常数高阶平均曲率

Journal of Zhejiang University(Science Edition), 2016,43(5):537-538,549

0　引　言

黎曼空间形式中超曲面的刚性问题，是黎曼几何学中最重要和最有意思的问题之一.

具有常数截面曲率的完备连通黎曼流形，即黎曼空间形式.就维数(n+1)而言，在微分同胚意义下，黎曼空间形式的代表有:欧氏空间Rn+1，有常数截面曲率K≡0;单位球面空间形式Sn+1，有常数截面曲率K≡1;单位双曲空间形式Hn+1，有常数截面曲率K≡-1.

BIVENS[1]对Hn+1中定向的紧致无边超曲面的刚性给出了如下的定理1.

定理1(文献[1]定理1)设Mn是Hn+1中定向的紧致无边超曲面.如果存在某个整数r(1≤r≤n-1)使得高阶平均曲率Hr，Hr+1均为非零常数，则Mn全脐.

1998年KOH[2]利用文献[1]的积分公式，改进了定理1的曲率条件，给出了如下定理：

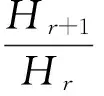
事实上，在外围空间为Rn+1和Sn+1的情况下，定理1和定理2也成立.定理1和定理2成为用高阶平均曲率来刻画超曲面的全脐性的经典结果.笔者注意到，定理1和定理2 的曲率条件，同时涉及2个高阶平均曲率.

ALENCAR等[3]研究了单位球面空间Sn+1中定向的紧致无边超曲面，得到了定理 3.定理3的曲率条件只涉及一个常数高阶平均曲率，但同时涉及超曲面的高斯映照像.

定理3(文献[3]定理B)设Mn是Sn+1中定向的紧致无边超曲面.假设存在某个整数r(1≤r≤n-1)使得高阶平均曲率Hr是常数，而且下列不等式处处成立:

Hr-1≥0，H1Hr-1≥Hr>0.

如果Mn的高斯映照像包含在一个闭的半球面内，则Mn全脐.

本文讨论Hn+1中定向的紧致无边超曲面，获得了定理A.与定理3类似，定理A的条件，也只涉及一个常数高阶平均曲率，同时与超曲面的高斯映照像相关.

定理A设Mn是Hn+1中定向的紧致无边超曲面.假设存在某个整数r(1≤r≤n-1)使得高阶平均曲率Hi>0，i=1,2,…,r，且Hr是常数.如果Mn的高斯映照像包含在一个开的半球面内，则Mn全脐.

注事实上，在外围空间为单位de Sitter空间的情况，用与本文类似的方法，可以证明与定理A类似的结论也成立.

1　预备知识

设Rn+2是(n+2)-维实向量空间.对

x=(x0,x1,...,xn+1),y=(y0,y1,...,yn+1)∈Rn+2，赋予如下的Lorentz内积[4-7]

(n+1)-维单位双曲空间形式Hn+1定义为[5]

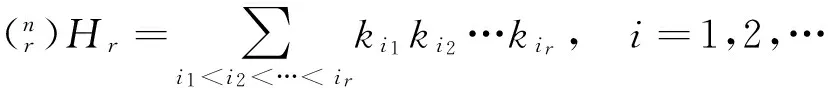
同时定义H0≡1.

因为高阶平均曲率是主曲率的基本对称函数的平均值，所以有下列不等式[1-4,8]：

(1)

进一步，当且仅当k1=k2=…=kn，式(1)中的等号成立.

当Mn是Hn+1中可定向的超曲面时，Mn有整体的单位法向量场N，且Mn的高斯映照像为[5]

N(M)={N(x)∈Tx(Hn+1):

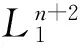
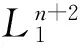
∫M(Hk-1〈x,p〉+Hk〈N,p〉)dx=0.

(2)

2　定理A的证明

证明首先，由假设Hi>0，i=1,2,…,r以及不等式(1)，有

(3)

由积分公式(2)，有

∫M(〈x,p〉+H1〈N,p〉)d x=0,

(4)

∫M(Hr〈x,p〉+Hr+1〈N,p〉)d x=0.

(5)

因为Hr是常数，由式(4)，有

∫M(Hr〈x,p〉+H1Hr〈N,p〉)dx=0.

(6)

由式(5)和(6)，立即得到

∫M(H1Hr-Hr+1)〈N,p〉d x=0.

(7)

注意到式(3)，有

H1Hr-Hr+1≥0，∀x∈Mn.

(8)

写Mn的单位法向量场为

∀x∈Mn.

因为假设Mn的高斯映照像N(Mn)包含在一个开半球面内，不失一般性，设

τ0(x)>0,∀x∈Mn.

〈N,p〉=〈N(x),p〉=-(-1)τ0(x)=τ0(x)>0.

(9)

最后，由式(7)～(9)，得式(3)中的全部等号成立.

再由式(1)等号成立的条件，证得Mn全脐.

[1]BIVENSI.Integralformulasandhypersphereinasimplyconnectedspaceform[J]. Proc Amer Math Soc,1983,88(1):113-118.

[2]KOH S E. A characterization of round spheres[J].Proc Amer Math Soc,1998,126(12):3657-3660.

[3]ALENCAR H, ROSENBERG H, SANTOS W. On the Gauss map of hyper-surfaces with constant scalar curvature in spheres[J]. Proc Amer Math Soc,2004,132(12):3731-3739.

[4]LI Haizhong, CHEN Weihuan. Integral formulas for compact space-like hyper-surfaces in de Sitter space and their applications to Goddard’s conjecture[J]. Acta Mathematica Sinica,1998,14(2):285-288.

[5]忻元龙.黎曼几何讲义[M].上海:复旦大学出版社,2010.

XIN Yuanlong. Riemann Geometry Notes[M]. Shanghai：Fudan University Press，2010.

[6]杨世国,王文,卞革.双曲空间Hn(-1)和球面空间Sn(1)中单形顶点角的一些不等式[J].数学学报,2014,57(6):1101-1108.

YANG Shiguo, WANG Wen, BIAN Ge. Inequalities for vertex angles of a simplex in hyperbolic space

Hn(-1) and spherical spaceSn(1)[J]. Acta Mathematica Sinica: Chinese Series,2014,57(6):1101-1108.

[7]聂昌雄,田大平,吴传喜.共形空间中具有平行的共形第二基本形式的I型类时超曲面[J].数学学报,2011,54(1):125-136.

NIE Changxiong, TIAN Daping, WU Chuanxi. Classification of type I time-like hyperspaces with parallel conformal second fundamental forms in the conformal space[J]. Acta Mathematica Sinica: Chinese Series,2011,54(1):125-136.

[8]HARDY G, LITTLEWOOD J, POLYA G. Inequalities[M]. Cambridge: Cambridge Univ Press,1989.

Totally umbilical hyper-surfaces of the hyperbolic space and the Gauss image.

WANG Qi

(SchoolofMathematicsandInformationScience,GuiyangUniversity,Guiyang550005,China)

LetMnbe a compact and oriented hyper-surface without boundary in the unit hyperbolic space formHn+1. Assume that thei-mean curvatureHi>0,i=1,2,…,rfor some integerr(1≤r≤n-1) and thatHris constant, We proved thatMnis totally umbilical if the Gauss image ofMnis contained in an open hemisphere.

unit hyperbolic space form; totally umbilical hyper-surface; Gauss image; constant higher order mean curvature