一个加强的Hardy-Hilbert型不等式

2016-09-16顾朝晖杨必成

浙江大学学报（理学版） 2016年5期

关键词：广东外语外贸大学朝晖等价

顾朝晖, 杨必成

(1. 广东外语外贸大学经济贸易学院，广东广州 510006； 2. 广东第二师范学院数学系，广东广州 510303)

一个加强的Hardy-Hilbert型不等式

顾朝晖1, 杨必成2

(1. 广东外语外贸大学经济贸易学院，广东广州 510006； 2. 广东第二师范学院数学系，广东广州 510303)

引入独立参数, 应用权系数的方法及Hadamard不等式, 建立了一个加强的具有最佳常数因子的Hardy- Hilbert型不等式及其等价形式.

Hardy-Hilbert型不等式; 参数; 权系数; 等价式; Hadamard不等式

Journal of Zhejiang University(Science Edition), 2016,43(5):532-536

0　引　言

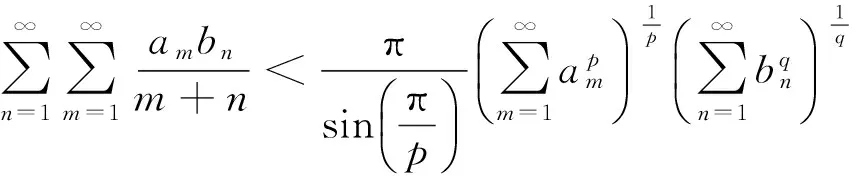
(1)

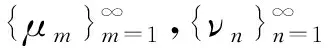
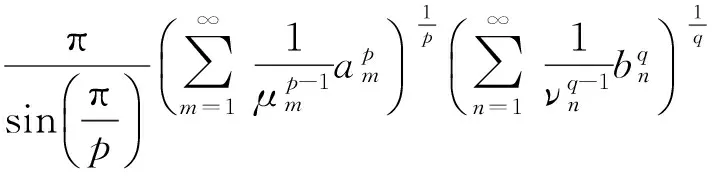
(2)

当μi=νi=1(i=1,2,…)时,式(2)即为式(1).

2015年,文献[6]引入独立参数α,λ>0,建立如下推广的Hardy-Hilbert型不等式:

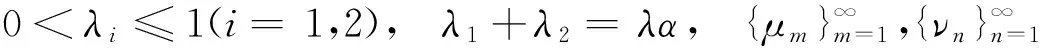
(3)

(4)

(5)

本文引入独立参数,应用权系数的方法及Hadamard不等式,建立具有最佳常数因子式(5)的加强式,还考虑了其等价形式.

1　引　理

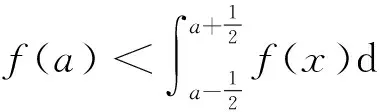
(6)

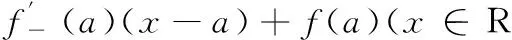
得式(6)成立.证毕.

例1设μ(t):=μm,t∈(m-1,m](m=1,2,…);v(t):=νn,t∈(n-1,n](n=1,2,…),

(7)

则

U(m)=Um,V(n)=Vn(m,n∈N).

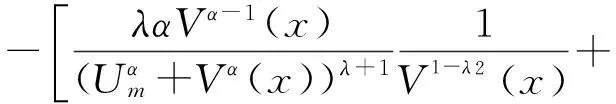
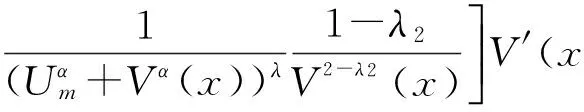
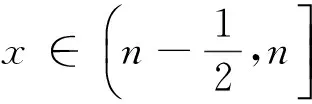
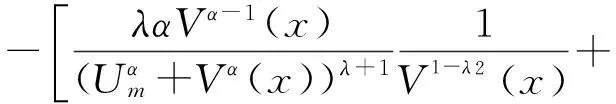
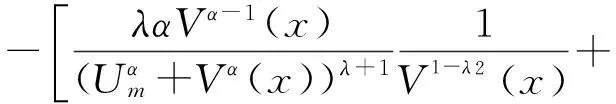
严格递增.可算得

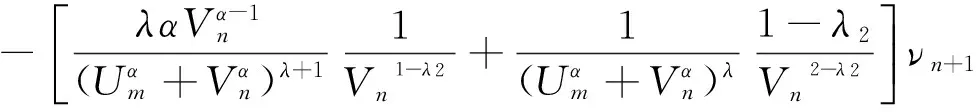
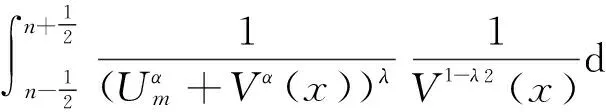
(8)

引理2定义如下权系数：

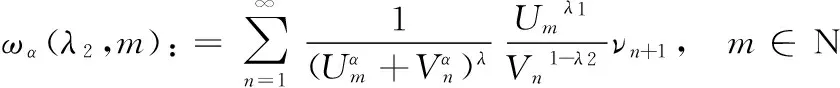
(9)

(10)

则有不等式:

0<λ2≤1,λ1>0,

ωα(λ2,m)<

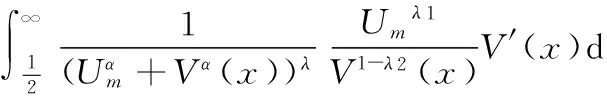
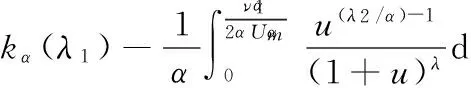
(13)

可估算得

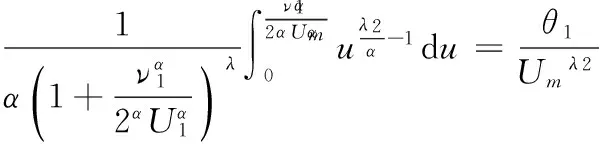
由式(13),可得式(11)成立.同理,由对称性,可证得式(12)成立.证毕.

引理3有如下权系数不等式:

kα(λ1)(1-θ1(λ2,m))<ωα(λ2,m)，m∈N;

0<λ2≤min{1,2-α},λ1>0,

(14)

kα(λ1)(1-θ2(λ1,n))<ϖα(λ1,n)，n∈N;

0<λ1≤min{1,2-α},λ2>0,

(15)

其中,

证明因f(x)严格递减及V(∞)=∞,有

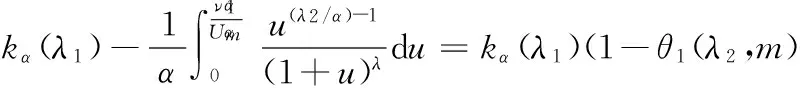
(16)

引理4对∀ε>0,有

(17)

(18)

证明由递减性质,有

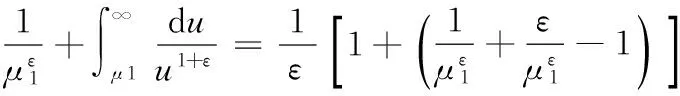
2　主要结果

(20)

(21)

(22)

(23)

由式(20),有式(21).反之,设式(21)成立.置

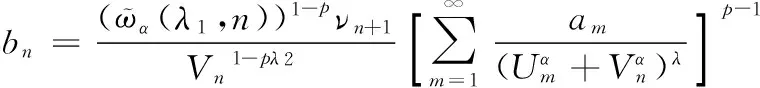
(24)

故式(20)成立,且它与式(19)等价.证毕.

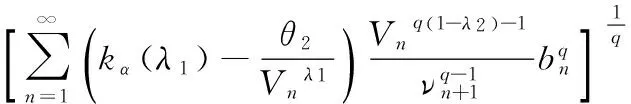
(25)

(26)

这里,常数因子kα(λ1)都为最佳值,θi(i=1,2)同引理2.

特别地,由式(25)可导出式(5);由式(26)可导出如下式(5)的等价式:

(27)

证明对式(19)、(20)，应用式(11)、(12),可得式(25)与(26)成立且等价.

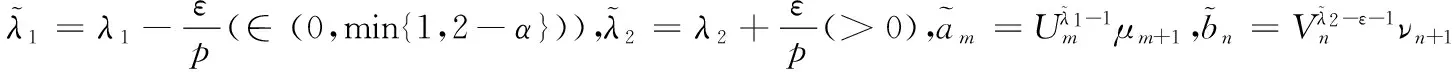
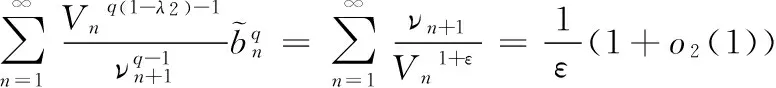
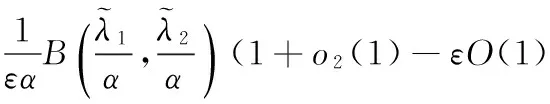
若有正常数K≤kα(λ1),使取代式(5)的常数因子kα(λ1)后仍成立.特别地，有

代入上式,有

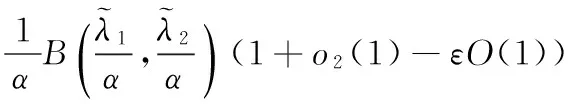
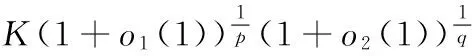
即有kα(λ1)≤K(ε→0+).故K=kα(λ1)为式(5)的最佳值.

式(27)的常数因子必为最佳值.不然,由式(23)(置ϖα(λ1,n)=1),必导出式(5)的常数因子也不为最佳值的矛盾结论.

同理，由反证法易证得式(25)、(26)的常数因子也为最佳值.证毕.

[1]HARDYGH.NoteonatheoremofHilbertconcerningseriesofpositiveterms[J]. Proceedings London Math Soc, 1925, 23(2):xlv-xlvi.

[2]HARDY G H, LITTLEWOOD J E, POLYA G. Inequalities[M]. Cambridge: Cambridge Univ Press, 1952.

[3]MITRINOVIC D S, PECARIC J E, FINK A M. Inequalities Involving Functions and Their Integrals and

Derivatives[M].Boston: Kluwer Academic Publishers, 1991.

[4]杨必成.算子范数与Hilbert型不等式[M].北京:科学出版社, 2009.

YANG Bicheng. The Norm of Operator and Hilbert-Type Inequalities[M]. Beijing: Science Press, 2009.

[5]YANG Bicheng. Discrete Hilbert-Type Inequalities[M]. Sharjah:Bentham Science Publishers Ltd, 2011.

[6]杨必成. 一个推广的Hardy-Hilbert型不等式[J].广东第二师范学院学报,2015, 35(3): 1-7.

YANG Bicheng. An extension of a Hardy-Hilbert-type inequality[J]. Journal of Guangdong University of Education, 2015, 35(3): 1-7.

[7]王竹溪,郭敦仁.特殊函数论[M].北京:科学出版社,1979.

WANG Zhuxi, GUO Dunren. Introduction of Special Functions[M]. Beijing: Science Press, 1979.

[8]匡继昌.常用不等式[M].济南:山东科技出版社, 2004.

KUANG Jichang. Applied Inequalities[M]. Jinan:Shandong Science and Technology Press, 2004.

A strengthened version of a Hardy-Hilbert-type inequality.

GU Zhaohui1, YANG Bicheng2

(1.SchoolofEconomics&Trade,GuangdongUniversityofForeignStudies,Guangzhou510006,China; 2.DepartmentofMathematics,GuangdongUniversityofEducation,Guangzhou510303,China)

Based on the weight coefficients, by applying of Hadamard’s inequality and introducing some independent parameters, a strengthened version of a Hardy-Hilbert-type inequality with a best possible constant factor is constructed. Meanwhile, its equivalent form is considered.

Hardy-Hilbert-type inequality; parameter; weight coefficient; equivalent form; Hadamard’s inequality