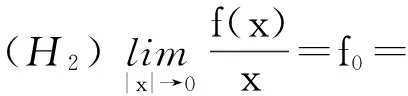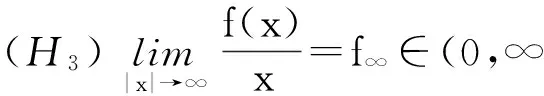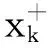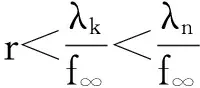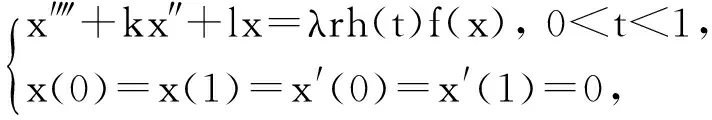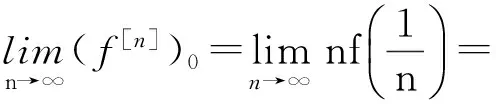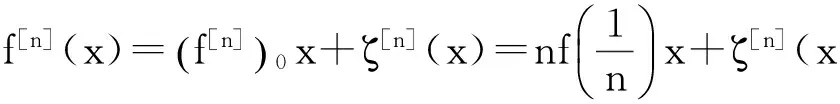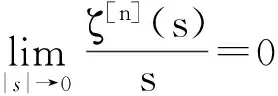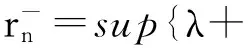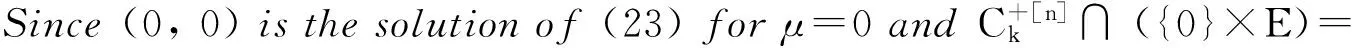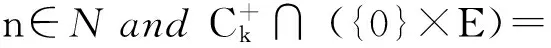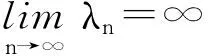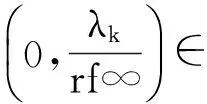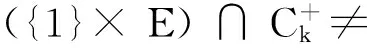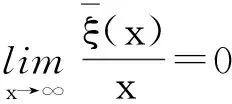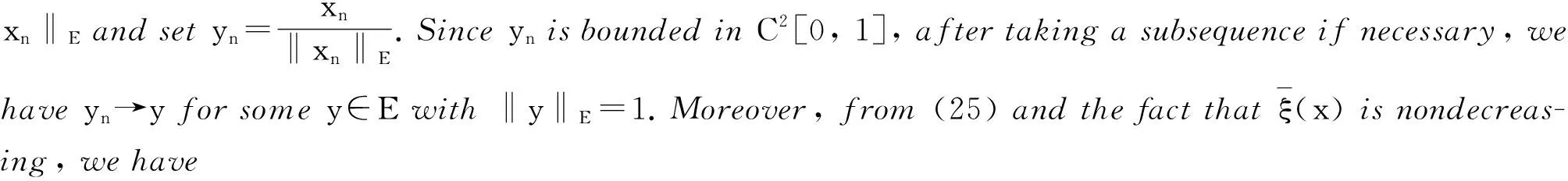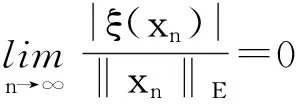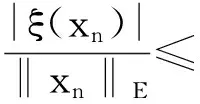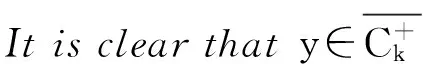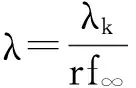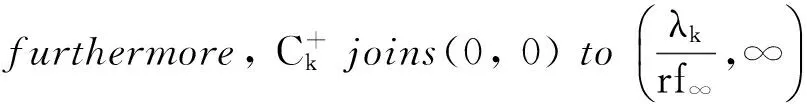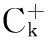Unilateral global bifurcation for fourth-order boundaryvalue problem with non-asymptotic nonlinearity at 0
2016-09-16SHENWenguo
SHEN Wenguo
(Department of Basic Courses, Lanzhou Institute of Technology, Lanzhou 730050, China)
Unilateral global bifurcation for fourth-order boundaryvalue problem with non-asymptotic nonlinearity at 0
SHEN Wenguo
(Department of Basic Courses, Lanzhou Institute of Technology, Lanzhou 730050, China)
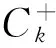
fourth-orderproblems;unilateralglobalbifurcation;nodalsolutions;non-asymptoticnon-linearityat0
浙江大学学报(理学版),2016,43(5):525-531
0 Introduction
LetEbearealBanachspacewiththenorm‖·‖.Considertheoperatorequation
u=λBu+H(λ, u),
(1)
whereBisacompactlinearoperatorandH:R×E→EiscompactwithH=o(‖u‖)atu=0uniformlyonboundedλintervals.
Rabinowitz’sglobalbifurcationtheorem[1]hasshownthatifthecharacteristicvalueμofBisofoddmultiplicityand
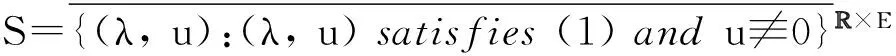
thenthereexistsacomponentCμofSthatcontains(μ, 0),whichsatisfies:
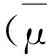
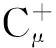
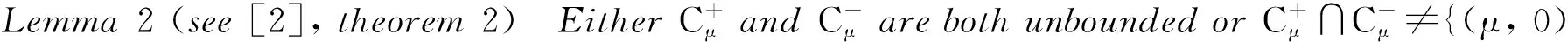
Recently,SHEN[3-4]studiedtheexistenceofnodalsolutionsofthefollowingboundaryvalueproblem:
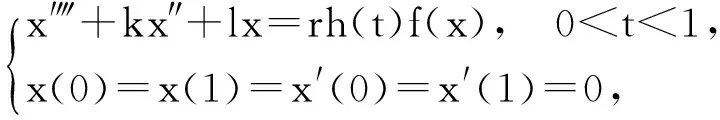
(2)
whereris a positive parameter, under the assumptions:
(A1) One of the following conditions holds:
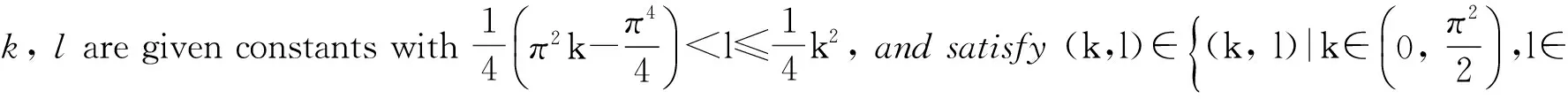
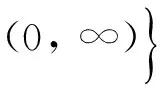
(A2) h(t) ∈C([0, 1], [0, ∞))withh(t)≢0onanysubintervalof[0, 1].
Lemma3[3-4](i)Thelineareigenvalueproblem

(3)
hasauniqueinfinitenumberofpositiveeigenvalues
0<λ1<λ2<…<λk<…→∞,ask→∞,
andtheeigenfunctionψkcorrespondingtoλkhasexactlyk-1zerosin(0, 1).
(ii)Foreachk∈N,thealgebraicmultiplicityofλkis1.
Meanwhile,RABINOWITZ[1]establishedunilateralglobalbifurcationtheory(theorem1.27andtheorem1.40of[1]).However,aspointedoutbyDANCER[2,5]andLPEZ-GMEZ[6],theproofsofthesetheoremscontaingaps.Fortunately,DANCER[2]gaveacorrectedversionoftheunilateralglobalbifurcationtheoremfortheproblem(1)whichhasbeenextendedtotheone-dimensionalp-LaplacianproblembyDAIetal.[7].In2013,DAIetal.[8]establishedaDancer-typeunilateralglobalbifurcationresultforfourth-orderproblemsofthedeformationsofanelasticbeaminequilibriumstatewhichbothendsaresimplysupported.
Motivatedbytheabovepapers,weshallestablishaDancer-typeunilateralglobalbifurcationresultaboutthecontinuumofsolutionsforthedeformationsofanelasticbeaminequilibriumstatewithfixedbothendpointswhichcanbedescribedbythefourth-orderproblems:
x′‴+kx″+lx=λh(t)x+g(t,x,λ), 0 x(0)=x(1)=x′(0)=x′(1)=0, (4) wherehsatisfies (A2), andg:(0, 1)×R2→Rsatisfies the Carathéodory condition in the first two variables, such that (5) uniformly fort∈ (0, 1) andλon bounded sets. Remark 1Since the problem (2) cannot transform into a system of second-order equation, the treatment method of second-order system does not apply to study the problem (2). Thus, existing literature on the problem (2) by bifurcation theory is limited[3-4,9]. Remark 2For other results on the existence and multiplicity of positive solutions and nodal solutions for other boundary value problems of fourth-order ordinary differential equations based on bifurcation techniques[10-11]. The rest of this paper is arranged as follows. In section 1, we establish the Dancer-type unilateral global bifurcation theory for problem (4). In section 2, we prove the existence of nodal solutions for the problem (2) under the linear growth condition onf. WedefinethelinearoperatorL:D(L)⊂E→Y, Lx=x′‴+kx″+lx, x∈ D(L) withD(L)= {x∈C4[0, 1]|x(0)=x(1)=x′(0)=x′(1)=0}.ThenLisaclosedoperatorandL-1:Y→Eiscompletelycontinuous. Define the operatorH:R×E→Eby H(λ,x)(t):=λL-1(hx)+L-1(g(t,x,λ))= Tλ(x)+L-1(g(t,x,λ)). It is easy to show thatI-Tλis a nonlinear compact perturbation of the identity. Thus the Leray-Schauder degree deg(I-Tλ,Br(0),0) is well-defined for arbitraryr-ballBr(0) andλ≠λk. Lemma 4For anyr>0, we have deg(I-Tλ,Br(0),0)= ProofSinceTλis compact and linear, by theorem 8.10 of [12], deg(I-Tλ,Br(0), 0)=(-1)m(λ), wherem(λ) is the sum of algebraic multiplicity of the eigenvaluesλof (3),satisfyλ-1λk<1. Ifλ∈ [0,λ1), by lemma 3, then there are no suchλat all, then deg(I-Tλ,Br(0), 0)=(-1)0=1. Ifλ∈(λk,λk+1) for somek∈N, then (λj)-1>1,j∈{1, 2,…,k}. By lemma 3, we obtain deg(I-Tλ,Br(0), 0)=(-1)k. Furthermore, it is clear that problem (4) can be equivalently written as x=H(λ,x)(t). Clearly,His completely continuous fromR×E→EandH(λ, 0)=0, ∀λ∈R. Let (6) (7) uniformlyfort∈ (0, 1)andλonboundedsets. Theorem1Assume(A1), (A2)and(5)hold.Then (i) (λk, 0)isabifurcationpointoftheproblem(4). Proof(i)Supposethat(λk, 0)isnotabifurcationpointofproblem(4).Thenthereexistε> 0,ρ0>0suchthatfor|λ-λk|≤εand0<ρ<ρ0thereisnonontrivialsolutionoftheequation x-H(λ, x)=0 with‖x‖=ρ.Fromtheinvarianceofthedegreeunderacompacthomo-topology,weobtainthat deg(I-H(λ, ·),Bρ(0), 0)≡constant (8) forλ∈[λk-ε,λk+ε]. By takingεsmaller if necessary, we can assume that there is no eigenvalue of (3) inλ∈(λk,λk+ε]. Fixλ∈(λk,λk+ε]. We claim that the equation x-(λL-1(hx)+τL-1(g(t,x,λ)))=0 (9)hasnosolutionxwith‖x‖=ρforeveryτ∈[0, 1]andρsufficientlysmall.Supposeonthecontrary,let{xn}bethesolutionof(9)with‖xn‖→0asn →+∞. (10) By(7), (10)andthecompactnessofL-1,choosingasubsequenceandrelabelingifnecessary,itfollowsthatyn→y0asn→∞.Thus Ly0=λhy0and‖y0‖E=1. Thisimpliesthatλisaneigenvalueof(3).Thisisacontradiction.Fromtheinvarianceofthedegreeunderhomo-topologyandlemma4,thenobtain deg(I- H(λ, ·),Bρ(0), 0)= deg(Ψλ,Bρ(0), 0)=(-1)k. (11) Similarly, forλ∈[λk-ε,λk), we find that deg(I-H(λ, ·),Bρ(0), 0)=(-1)k-1. (12) Relations (11) and (12) contradicts (8) and hence (λk, 0) is a bifurcation point of problem (4). (ii) By (7), we have that (13) uniformlyt∈(0, 1) andλon bounded sets. Furthermore, by (ii) of lemma 3, applying lemma 2, we can obtain the result. (14) By(7), (14)andthecompactnessofL-1,weobtainthatforsomeconvenientsubsequenceym→y0asm→+∞.Nowy0verifiestheequation Ly0=λjhy0and‖y0‖E=1. Hencey0∈SjwhichisanopensetinE,andasaconsequenceforsomemlargeenough, ym∈Sj,andthisisacontradiction. Lemma6If(λ, u)isasolutionof(4)andx∈∂Sk,thenx≡0. ProofBytheproofoftheorem3.1in[13] (seecorollary1.12andtheproofoftheorem2.3togetherwiththeremarkfollowingthatproofin[1]),weeasilyobtaintheresult. Bytheorem1andlemma5,wecaneasilydeducethefollowingDancer-typeunilateralglobalbifurcationresult. (15) (16) By(7), (16)andthecompactnessofL-1,weobtainthatforsomeconvenientsubsequencezm→z0asm→+∞.Nowz0verifiestheequation Lz0=λjhz0and‖z0‖E=1. (17) By(7), (17)andthecompactnessofL-1,weobtainthatforsomeconvenientsubsequenceyn→y0≠0asn→+∞.Nowy0verifiestheequation Ly0=λ*h(t)y0(t), t∈(0,1)and‖y0‖E=1. Inordertotreatthecasef0=∞,weshallneedthefollowinglemma. Definition1[14]LetXbeaBanachspaceand{Cn|n=1,2,…}beafamilyofsubsetsofX.ThenthesuperiorlimitDof{Cn}isdefinedby suchthatxni→x}. (18) Lemma 7[14]Each connected subset of metric spaceXis contained in a component, and each connected component ofXis closed. Lemma 8[15]LetXbe a Banach space and let {Cn|n=1, 2,…} be a family of closed connected subsets ofX. Assume that (i) there existszn∈Cn,n=1, 2,… andz*∈X, such thatzn→z*; (ii)rn=sup{‖x‖|x∈Cn}=∞; BR={x∈X|‖x‖≤R}. ThenthereexistsanunboundedconnectedcomponentCinDandz*∈C. Inordertoprovethemainresults,theconditions(A1), (A2)andthefollowingconditionsaresatisfiedinthefollowingpart: (H1) f∈C(R, R)satisfiesf(s)s>0fors≠0. Theorem3Let(A1), (A2), (H1), (H2)and(H3)hold.Assumefollowingconditionholdsforsomek∈N: Theorem4Let(A1), (A2), (H1), (H2)and(H3)hold.Assumefollowingconditionholdsforsomek, n∈Nwithk≤n: Proofoftheorem3Firstly,westudythebifurcationphenomenaforthefollowingeigenvalueproblem: (19) whereλ>0isaparameter.Itisclearthatanysolutionof(19)oftheform(1,x)yieldssolutionsxof(2). Foreachn∈N,definef[n](s):R→Rby Clearly,by(H2),wehave Nowconsidertheauxiliaryfamilyoftheequations (20) Letζ[n]∈C(R, R)suchthat (21) Then (22) Letusconsider (23)asabifurcationproblemfromthetrivialsolutionx≡0. Equation(23)canbeconvertedtotheequivalentequation x:=λL-1[a[n](·)x(·)](t)+ λL-1[ζ[n](·x(·))](t). (24) Clearly, ‖L-1[ζ[n](·,x(·))]‖E=o(‖x‖E),as‖x‖E→0. Since λn+‖xn‖→∞. If then andmoreover, AssumethatthereexistsaconstantnumberM>0suchthatforalln∈N, λn∈ (0,M], Inthiscase,itfollowsthat‖xn‖E→∞. Letξ∈C(R, R)suchthat f(x)= f∞x+ξ(x). Then Let (25) Wedividetheequation (26) since Thus y′‴+ky″+ly=λra(t)f∞y. Weclaimthat Proofofthetheorem4Usingthesimilarproofwiththatoftheorem3,wecanobtaintheresult. [1]RABINOWITZPH.Someglobalresultsfornonlineareigenvalueproblems[J].JFunctAnal,1971(7):487-513. [2]DANCER E N. On the structure of solutions of non-linear eigenvalue problems[J]. Indiana University Math J,1974,23:1069-1076. [3]SHEN W G. Global structure of nodal solutions for a fourth-order two-point boundary value problem[J]. Applied Mathematics and Computation,2012,219(1):88-98. [4]SHEN W G. Existence of nodal solutions of a nonlinear fourth-order two-point boundary value problem[J]. Boundary Value Problems,2012,2012(1):1-18.doi:10.1186/1687-2770-2012-31. [5]DANCER E N. Bifurcation from simple eigenvaluses and eigenvalues of geometric multiplicity one[J]. Bull Lond Math Soc,2002, 34:533-538. Hall,2001. [7]DAI G W, MA R Y. Unilateral global bifurcation phenomena and nodal solutions forp-Laplacian[J]. J Differ Equ,2012,252:2448-2468. [8]DAI G W, HAN X L. Global bifurcation and nodal solutions for fourth-order problems with sign-changing weight[J]. Applied Mathematics and Computation,2013,219:9399-9407. [9]KORMAN P. Uniqueness and exact multiplicity of solutions for a class of fourth-order semilinear problems[J]. Proceedings of the Royal Society of Edinburgh A,2004,134(1):179-190. [10]MA R Y, GAO C H, HAN X L. On linear and nonlinear fourth-order eigenvalue problems with indefinite weight[J]. Nonlinear Anal Theory Methods Appl,2011,74(18):6965-6969. [11]MA R Y, GAO C H. Nodal solutions of a nonlinear eigenvalue problem of the Euler-Bernoulli equation[J]. Math Anal Appl,2012,387(2):1160-1166. [12]DEIMLING K. Nonlinear Functional Analysis[M]. New York: Springer-Verlag,1987. [13]RYNNE B P. Global bifurcation for 2mth-order boundary value problems and infinitely many solu-tions of superlinear problems[J]. J Differential Equations,2003,188:461-472. [14]WHYBURN G T. Topological Analysis, Princeton Mathematical Series No.23[M]. New Jersey: Princeton University Press,1958. [15]MA R Y, AN Y L. Global structure of positive for superlinear second-orderm-point boundary value problems[J]. Topological Methods in Nonlinear Analysis,2009,34(2):279-290. 10.3785/j.issn.1008-9497.2016.05.005 非线性项在零点非渐进增长的四阶边值问题单侧全局分歧. 沈文国 (兰州工业学院, 基础学科部, 甘肃 兰州 730050) 四阶问题;单侧全局分歧;结点解;非线性项在零点非渐进增长 O175.8 A 1008-9497(2016)05-525-07 date:August 1,2015. Supported by the National Natural Science Foundation of China (11561038); the Gansu Provincial Natural Science Foundation(145RJZA087). About the author:SHEN Wenguo (1963-), ORCID:http://orcid.org/0000-0001-7323-1887, Doctor, Professor, the field of interest is nonlinear functional differential equations,E-mail: shenwg369@163.com.
1 Unilateral global bifurcation results
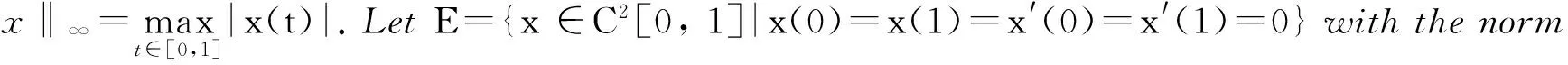
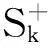
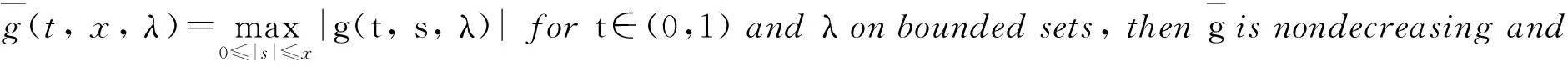

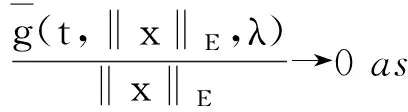
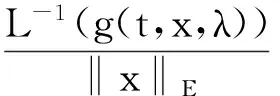
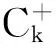
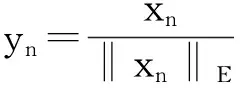
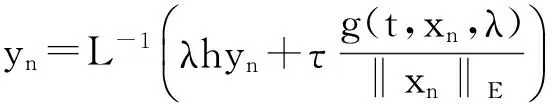
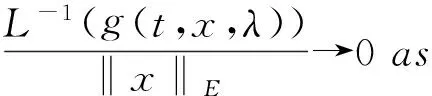
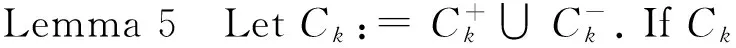
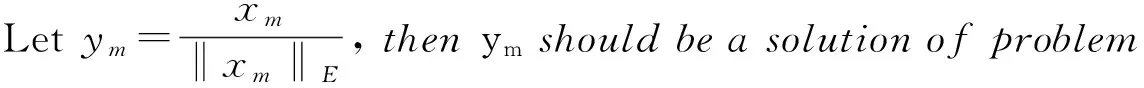
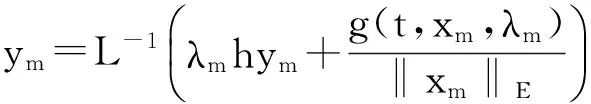
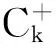
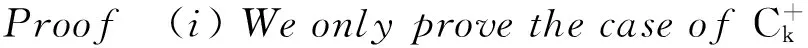
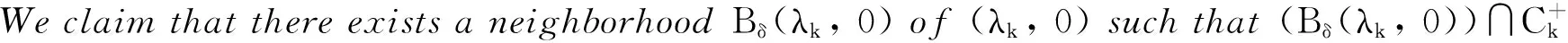
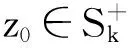
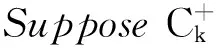
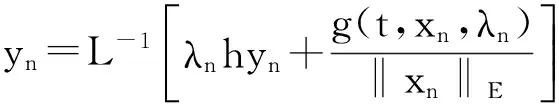
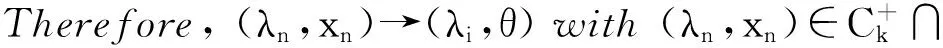
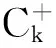
2 Main results