微分多项式环的半交换性和对称性

2016-09-16任艳丽张玖琳

浙江大学学报（理学版） 2016年5期

关键词：正整数微分对称性

任艳丽, 张玖琳, 王　尧

(1. 南京晓庄学院数学与信息技术学院, 江苏南京 211171; 2. 南京信息工程大学数学与统计学院, 江苏南京 210044)

微分多项式环的半交换性和对称性

任艳丽1, 张玖琳2, 王尧2

(1. 南京晓庄学院数学与信息技术学院, 江苏南京 211171; 2. 南京信息工程大学数学与统计学院, 江苏南京 210044)

研究微分多项式环R[x;δ]和Ore扩张环R[x;α,δ]的广义半交换性质和广义对称性质,使用逐项分析方法证明了：设R是δ-Armendariz环, 则R[x;δ]是诣零半交换环(弱半交换环、广义弱对称环、弱zip环、右弱McCoy环)当且仅当R是诣零半交换环(弱半交换环、广义弱对称环、弱zip环、右弱McCoy环);设R是弱2-素环和(α,δ)-条件环,则R[x;α,δ]是诣零半交换环(分别地,弱半交换环,广义弱对称环).

弱2-素环;δ-Armendariz环; (α,δ)-条件环; 诣零半交换环; 广义弱对称环

Journal of Zhejiang University(Science Edition), 2016,43(5):505-511

0　引　言

对于一个给定的环, 文献[9-10]讨论了其斜多项式环的诣零半交换性和弱半交换性, 本文将在第1节讨论其微分多项式环的诣零半交换性和弱半交换性.文献 [11] 在δ-容许环和诣零半交换环的条件下研究了微分多项式环R[x;δ] 的弱 McCoy 性, 本文第2节将在δ-Armendariz 条件下继续研究其微分多项式扩张的广义弱对称性、弱 zip 性和弱 McCoy 性. 文献 [3] 证明了如果R是 (α,δ)-容许环、可逆环, 则 Ore 扩张环R[x;α,δ]是弱对称环当且仅当R是弱对称环. 本文第3节将在弱 2-素环和 (α,δ)-条件环下讨论给定环的 Ore 扩张环R[x;α,δ] 的弱对称性和诣零半交换性, 给出一般 Ore 扩张环R[x;α,δ] 是广义弱对称环的充要条件.

1　广义半交换性

设δ:R→R是环R上的一个导子, 对∀a∈R, 有

引理1设R是一个δ-Armendariz 环,

(1) 如果对于某个正整数n,ab=cn=0, 则acb=0, 其中a，b，c∈R;

(2) 如果f1,f2, …,fn∈R[x;δ],f1f2…fn=0, 则a1a2…an=0, 其中,对∀i，ai是fi的任意系数;

(3) 如果a1a2…an=0, 则对∀ai∈R, 任意的非负整数ri和n, 1≤i≤n,有δr1(a1)δr2(a2) …δrn(an)=0.

证明由文献 [5] 中定理 2.7、命题 2.9 和引理 2.10 即知.

引理 2设R是一个δ-Armendariz 环,

(1) 如果a∈ nil(R), 则对任意的正整数k，δk(a)∈ nil(R);

(2) 如果a∈ nil(R),b∈ nil(R), 则ab∈ nil(R);

(3) 如果a∈ nil(R),b∈ nil(R), 则a+b∈ nil(R).

证明(1)存在正整数n使得an=0. 由引理 1(3) 知，δk(a)δk(a)…δk(a)=0,故(δk(a))n=0, 从而δk(a)∈ nil(R).

(2)存在正整数m,n, 使得am=0,bn=0. 根据引理 1(1)，知abab…a=0, 于是有 (ab)m=0,ab∈ nil(R).

(3)不妨设am=0,bm=0. 下证 (a+b)2m=0. (a+b)2m的每一项可以表示为长度为 2m的单项式, 设为u1u2…u2m, 其中ui∈{a,b}.a和b中必有一个元素在此单项式里至少出现m次, 设a出现k≥m次, 则ak=0. 这样,u1u2…u2m=b1ab2a…bkabk+1, 其中bj∈{bn|0≤n≤2m-k}, 1≤j≤k+1. 由于R是一个δ-Armendariz 环,b∈ nil(R), 根据引理2(2),对任意的1≤j≤k+1，可得bj∈ nil(R). 由于ak=0, 再根据引理 1(1) 可推出ab2a…bka=0, 从而有b1ab2a…bkabk+1=0. 即证得(a+b)2m=0,a+b∈ nil(R).

定理1设R是δ-Armendariz 环, 则 nil(R) 是R的一个子环.

证明由引理 2 可得.

推论1设R是Armendariz 环, 则 nil(R) 是R的一个子环.

定理2设R是δ-Armendariz 环, 则有 nil(R[x;δ])= nil(R)[x;δ].

由此可见, 多项式f(x)(n+1)k的每一单项式的系数都可以写为形如

的和, 其中aij∈{a0,a1,…,an}, 1≤j≤(n+1)k,tp(2≤p≤(n+1)k),u和v是正整数. 这里ai1δt2(ai2)…δt(n+1)k(ai(n+1)k) 中必有一个元素aj0(0≤j0≤n) 至少出现k次, 于是它又可以写为

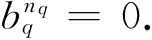
(δs1(aj0))j1(δs2(aj0))j2… (δsw(aj0))jw=0.

再由引理 1(1) 可以推出b1(δs1(aj0))j1b2(δs2(aj0))j2…bw(δsw(aj0))jwbw+1=0.

证得f(x)(n+1)k=0, 所以f(x)∈ nil(R[x;δ]).

推论2设R是Armendariz环,则有nil(R[x])=nil(R)[x].

定理3设R是δ-Armendariz 环, 则R[x;δ] 是诣零半交换环当且仅当R是诣零半交换环.

证明充分性. 设f(x)g(x)∈ nil(R[x;δ]), 则存在正整数k使得 (f(x)g(x))k=0. 由引理 1(2) 知 (aibj)k=0, 对任意的0≤i≤n, 0≤j≤m, 即有aibj∈ nil(R). 由于R是诣零半交换环, 所以对任意的r∈R, 有airbj∈ nil(R), 即存在正整数h使得 (airbj)h=airbjairbj…airbj=0. 根据引理 1(3), 对任意正整数s和t, 可推出

aiδs(r)δt(bj)aiδs(r)δt(bj) …aiδs(r)δt(bj)=

(aiδs(r)δt(bj))h=0,aiδs(r)δt(bj)∈ nil(R).

由定理 1, nil(R) 是R的一个子环, 从而有 ∑aiδs(r)δt(bj)∈ nil(R), 因此对任意的h(x)∈R[x;δ], 有f(x)h(x)g(x)∈ nil(R)[x;δ]. 再由定理 2, 有f(x)h(x)g(x)∈ nil(R[x;δ]), 故R[x;δ] 是诣零半交换环.

必要性. 由诣零半交换环的子环仍是诣零半交换环即得.

推论3设R是Armendariz 环, 则R[x] 是诣零半交换环当且仅当R是诣零半交换环.

定理4设R是δ-Armendariz 环, 则R[x;δ] 是弱半交换环当且仅当R是弱半交换环.

aiδs(r)δt(bj)aiδs(r)δt(bj)…aiδs(r)δt(bj)=

(aiδs(r)δt(bj))k=0,aiδs(r)δt(bj)∈ nil(R),

对任意正整数s和t. 再由定理 1 知

∑aiδs(r)δt(bj)∈ nil(R).

于是,对任意的h(x)∈R[x;δ],有

f(x)h(x)g(x)∈nil(R)[x;δ].

据定理2,有

f(x)h(x)g(x)∈nil(R[x;δ]),

因此R[x;δ]是弱半交换环.

必要性. 由弱半交换环的子环仍是弱半交换环立得.

推论4设R是Armendariz 环, 则R[x] 是弱半交换环当且仅当R是弱半交换环.

引理3[5]设R是δ-Armendariz 环, 则有J(R[x;δ])= nil*(R)[x;δ].

定理5设R是δ-Armendariz 环. 如果R还是 NJ 环, 则R[x;δ] 是 J-半交换环.

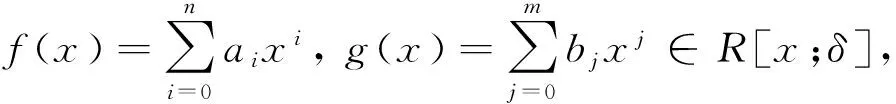
2　广义弱对称性、弱zip性和弱McCoy性

定理6设R是δ-Armendariz环,则R[x;δ]是广义弱对称环当且仅当R是广义弱对称环.

必要性.由广义弱对称环的子环仍是广义弱对称环立得.

定理7设R是δ-Armendariz 环, 则R[x;δ] 是弱 zip 环当且仅当R是弱 zip 环.

证明充分性. 设X⊆R[x;δ] 满足NR[x;δ](X)⊆ nil(R[x;δ]). 以下以CX表示X中一切多项式的系数的集合. 下证NR(CX)⊆ nil(R).

Δ0+Δ1x+…+Δsxs+…+Δmxm.由nil(R)是R的一个子环知,对任意的0≤j≤m,Δj∈nil(R).因此,根据定理2可得f(x)r∈nil(R[x;δ]).于是有r∈NR[x;δ](X)⊆nil(R[x;δ]),从而有NR(CX)⊆nil(R).已知R是弱zip环,存在一个有限子集Y′⊆CX满足NR(Y′)⊆nil(R).由CX的定义,对任意的b∈Y′,一定存在多项式gb(x)∈X使得gb(x)的某个系数是b.取X′是X的一个极小子集,使其满足对任意的b∈Y′,有gb(x)∈X′.X′是X的一个有限子集.显然Y′⊆CX′,因此NR(CX′)⊆NR(Y′)⊆nil(R).

再证NR[x;δ](X′)⊆nil(R[x;δ]).

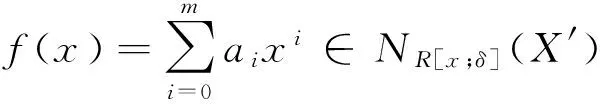
定理8设R是δ-Armendariz环,则R[x;δ]是右弱McCoy环当且仅当R是右弱McCoy环.

Δ0+Δ1x+…+Δtxt+…+Δpixpi,

由定理1知，对任意的0≤j≤pi,Δj∈nil(R).于是,由定理2可得对任意的0≤i≤m,fir∈nil(R[x;δ]).所以R[x;δ]是右弱McCoy环.

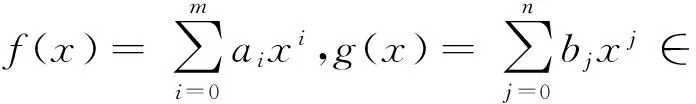
3　Ore扩张的诣零半交换性和广义弱对称性

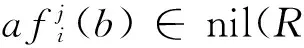
引理6设R是弱2-素环和(α,δ)-条件环,

(1)对任意的整数0≤i≤n，如果f(x)=a0+a1x+…+anxn,则f(x)∈nil(R[x;α,δ])当且仅当ai∈nil(R);

(2)对任意a,b∈R和正整数m,如果aαm(b)∈nil(R),则ab∈nil(R).

nil(R)[x;α,δ],

其中h2(x)∈R[x;α,δ]且次数低于(n-1)k,从而有an-1αn-1(an-1)…α(k-1)(n-1)(an-1)∈nil(R).利用R的(α,δ)-条件,可推出an-1∈nil(R).依此类推,对任意的0≤i≤n,最后可得ai∈nil(R).

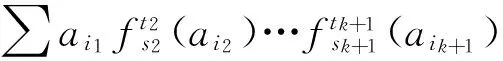
(2)设aαm(b)∈ nil(R), 其中m是正整数, 则有αm(b)a∈ nil(R). 由引理 5 可得αm(b)αm(a)∈ nil(R). 因为R是弱 2-素环, 从而 nil(R) 是R的一个理想, 所以baαm(ba)∈ nil(R). 由R是弱α-刚性环, 又有ba∈ nil(R), 因此ab∈ nil(R).

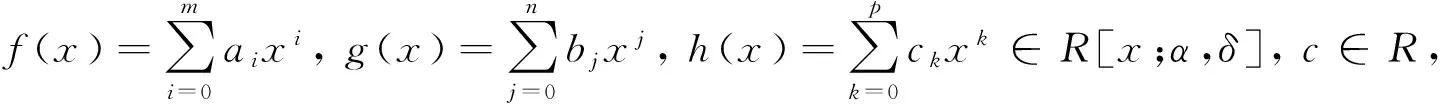
(1) 对任意的 0≤i≤m, 0≤j≤n，有f(x)g(x)∈ nil(R[x;α,δ]) 当且仅当aibj∈ nil(R);

(2) 对任意的 0≤i≤m, 0≤j≤n，有f(x)g(x)c∈ nil(R[x;α,δ]) 当且仅当aibjc∈ nil(R);

(3) 对任意的 0≤i≤m, 0≤j≤n, 0≤k≤p,有f(x)g(x)h(x)∈ nil(R[x;α,δ]) 当且仅当aibjck∈ nil(R).

证明(1) 必要性. 设f(x)g(x)∈ nil(R[x;α,δ]), 对于

…+amαm(bn)xm+n=

Δ0+Δ1x+…+Δkxk…+Δm+nxm+n,

bnam-1αm-1(bn)αm-1(am-1)∈ nil(R),

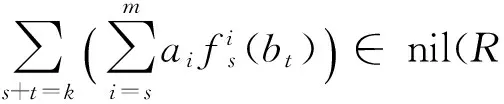
利用引理7(1)、引理5和引理6(2),类似文献[3]定理2.11的证明，可证得引理7(2)和(3).

文献[6]在(α,δ)-条件环和可逆环下研究了Ore扩张的弱zip性质,本文在(α,δ)-条件环和弱2-素环下，研究Ore扩张的诣零半交换性和弱对称性.

定理9设R是弱2-素环和(α,δ)-条件环,则R[x;α,δ]是诣零半交换环.

推论5设R是弱2-素环和(α,δ)-条件环,则R[x;α,δ]是弱半交换环.

定理10设R是弱2-素环和(α,δ)-条件环,则R[x;α,δ]是弱对称环当且仅当R是弱对称环.

证明因为弱对称环的子环仍是弱对称环,必要性显然成立.下证充分性.

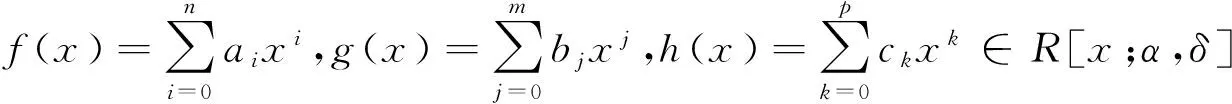
推论6[3]设R是可逆环和 (α,δ)-条件环, 则R[x;α,δ] 是弱对称环当且仅当R是弱对称环.

定理11设R是对称环和 (α,δ)-条件环, 则R[x;α,δ] 是广义弱对称环.

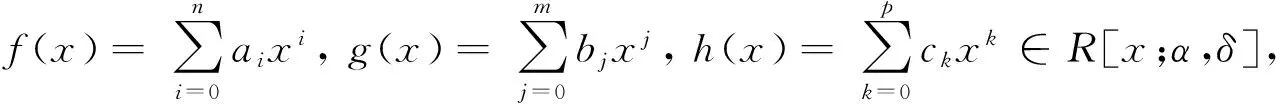
[1]KIMHK,KIMNK,JEONGMS,etal.Onconditionsprovidedbynilradicals[J]. J Korean Math Soc,2009,46(5):1027-1040.

[2]XIE Xue. Some results on J-semicommutative rings[J]. Mathematical Theory and Applications,2012,32(2):26-32.

[3]OUYANG Lunqun, CHEN Huanyin. On weak symmetric rings[J]. Comm Algebra,2010,38(2):697-713.

[4]WEI Junchao. Generalized weakly symmetric rings[J]. J Pure Appl Algebra,2014,218(9):1594-1603.

[5]NASR-ISFAHANI A R, MOUSSAVI A. A generalization of reduced rings[J]. J Algebra Appl,2012,11(4):1250070.1-1250070.30.

[6]MOHAMMADI R, MOUSSAVI A, ZAHIRI M. On weak zip skew polynomial rings[J]. Asian European J Math,2012,5(3):3901-3917.

[7]OUYANG Lunqun. Ore extensions of weak zip rings[J]. Glasgow Math J,2009,51(3):525-537.

[8]GHALANDARZADEH S, KHORAMDEL M. On weak McCoy rings[J]. Thai J Math,2008,6(2):337-342.

[9]CHEN Weixing. On nil-semicommutative rings[J]. Thai J Math,2011,9(1):39-47.

[10]CHEN Weixing, CUI Shuying. On weakly semicommutative rings[J]. Communications in Mathematical Research,2011,27(2):179-192.

[11]MOHAMMADI R, MOUSSAVI A, ZAHIRI M. Weak McCoy Ore extensions[J]. Int Math Forum,2011,6(2):75-86.

The semicommutativity and symmetry of differential polynomial rings.

REN Yanli1, ZHANG Jiulin2, WANG Yao2

(1.SchoolofMathematicsandInformationTechnology,NanjingXiaozhuangUniversity,Nanjing211171,China; 2.SchoolofMathematicsandStatistics,NanjingUniversityofInformationScienceandTechnology,Nanjing210044,China)

This paper investigates the generalized semicommutativity and generalized symmetry of the differential polynomial rings and Ore extensions of a ring. By using the itemized analysis method on polynomials, we proved that ifRisδ-Armendariz ring, thenR[x;δ] is nil-semicommutative ring (resp., weakly semicommutative, generalized weak symmetry (GWS), weak zip, right weak McCoy) if and only ifRis nil-semicommutative ring (resp., weakly semicommutative, GWS, weak zip, right weak McCoy). Moreover, ifRis a weakly 2-primal and (α,δ)-condition ring, thenR[x;α,δ] is nil-semicommutative ring (resp., weakly semicommutative, GWS).

weakly 2-primal ring;δ-Armendariz ring; (α,δ)-condition ring; nil-semicommutative ring; generalized weak symmetry ring