汽车仪表板加强管柱振动疲劳CAE分析

闫瑞华

（中国第一汽车股份有限公司天津技术开发分公司）

汽车行驶时将承受由路面不平顺产生的振动载荷和发动机产生的振动载荷，车身及底盘零部件若出现振动疲劳损伤，将严重地影响汽车结构的安全性和可靠性。为保证汽车的性能安全，各车型上市前主机厂都会进行台架试验和强化坏路等试验，以保证汽车的各项性能满足国家和企业内部的规范及标准。但由于试制汽车和路试试验会大大延长开发周期增加开发成本，因此基于CAE仿真分析的车辆疲劳强度性能评估，成为一种有效预测和解决此类问题的方法。文章使用有限元方法对某车型仪表板加强管柱及支架做振动疲劳CAE分析。通过与试验结果的对比，验证CAE分析结果的准确性。

1 模态叠加原理

模态是机械结构的固有振动特性，每一阶模态具有特定的固有频率、阻尼比及模态振型。这些模态参数可以由计算或试验分析取得。在计算机械结构响应时，可将线性定常系统振动微分方程组中的物理坐标变换为模态坐标，使方程组解耦，成为1组以模态坐标及模态参数描述的独立方程[1]。多自由度系统的微分方程，如式（1）所示。

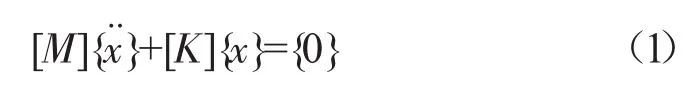
式中：[M]——质量矩阵（非对角矩阵），t；

[K]——刚度矩阵（非对角矩阵），N/mm；

{x}——固有振型位移矩阵，mm；

{0}——零矩阵，N；

系统在做无阻尼自由振动时，具有确定的一系列固有频率及相应的固有振型，那么该系统的任一实际振动{x}可用该固有振型之线性叠加来表示，如式（2）所示。

式中：{q}——变换后的新坐标矩阵，mm；

{Φ}——转换矩阵（各列向量之间线性独立）；

q1，q2，…，qn——矩阵{q}的各向分量，mm；

{φ1}，{φ2}，…，{φn}——矩阵{Φ}的各向分量。

经过坐标变换可得1组无耦合方程，如式（3）所示，对该方程解耦即可求得模态参数。

式中：[Mr]——转换后的质量矩阵，t；

[Kr]——转换后刚度矩阵，N/mm；

以某平板钣金为例，j点为随机取点，L点为激励点，j点位移响应（Uj（ω））可由式（4）计算得出。

式中：Uj（ω）——j点位移响应，mm；

φi，j——i阶模态下j点的模态振型，由模态分析得出，mm；

qi——i阶模态参与因子；

ω——振动频率，Hz；

φi，L——i阶模态L点的模态振型，mm；

ωi——i阶模态振动频率，Hz；

FL（ω）——激励点L点的激励载荷，N。

2 试验状态和结果

根据企业标准，搭建仪表板加强管柱振动试验台架，如图1所示。截取部分车身前端，其中金属件包括：仪表板加强管柱分总成、转向管柱分总成、车身前围板、车身A柱分总成及部分前地板等零部件。塑料件包括：仪表板、空调通道、出风口及中央通道盒等塑料件。图1中，试件与试验台架在B柱底端、前地板底端及中央通道盒底端相连接，激励点位于试验台架与试验台相连接处。对同款车型截取2件同样试件，先后安装于此试验台架，完成振动疲劳试验2次，分别为试验A和试验B。试验A要求激励点振幅及加速度为企业标准值，试验B要求仪表板响应最大位置振幅及加速度为企业标准值。

图1 仪表板加强管柱振动试验台

此次振动试验主要关注仪表板加强管柱分总成钣金件的振动疲劳损伤。试验A中，仪表板加强管柱2号支架和3号支架根部断裂，如图2所示。试验B仪表板加强管柱钣金件无明显损伤。

图2 试验A仪表板加强管柱支架断裂实物图

3 模型和模态分析结果

为保证模态分析的准确性，依照试验状态截取车身零部件，保留汽车仪表板加强管柱分总成、车身前围板、部分前地板、部分车身A柱分总成、仪表板、空调通道、出风口及中央通道盒等零部件。使用HyperWorks软件对以上零部件建模，其中使用壳单元模拟钣金件，使用四面体单元模拟金属铸件，使用四面体单元模拟与仪表板加强管柱直接相连接的塑料件，使用质量点单元模拟与仪表板加强管柱非直接连接件，试验用支架使用简化梁单元模拟，如图3所示。图3中红色部件为振动疲劳试验关注的仪表板加强管柱分总成。

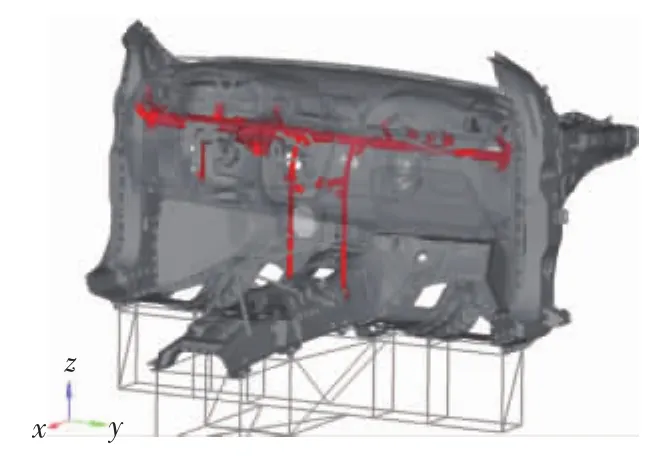
图3 加强管柱模型示意图

使用HyperWorks软件自带求解器optistruct对以上模型做模态分析计算，要求计算1～50 Hz范围内该有限元模型的模态，输出有限元模型的整体位移和仪表板加强管柱有限元模型的应力及应变，有限元分析结果输出为*.op2格式文件。

通过计算，在1～50 Hz频率范围内共求得15阶模态，各阶模态频率，如表1所示。

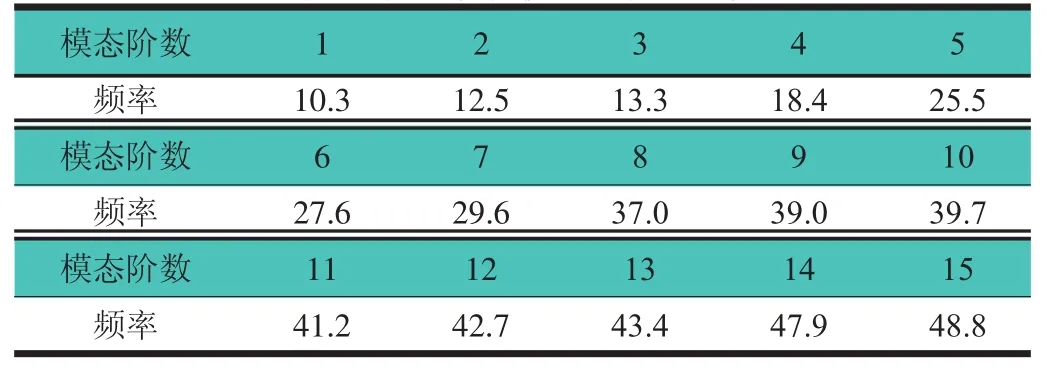
表1 加强管柱模态阶数与频率 Hz

4 振动疲劳分析

根据模态叠加原理，振动疲劳试验状态可由各阶模态叠加耦合而成。为叠加耦合试验状态的频率和振幅，首先要计算各阶模态的模态参与因子。将得出的模态分析结果导入LMS Virtual.Lab中，以1 Hz为计算精度，在1～50 Hz范围内对激励点施加激励，计算模态参与因子。经计算，本次分析模型的15阶模态参与因子分析结果，如图4所示。

图4 加强管柱模态参与因子分析截图

以模态参与因子结果为输入，定义谐波振动分析。在谐波振动分析中，要求定义振动频率和振动时间。振动频率（f）的计算，如式（5）所示。

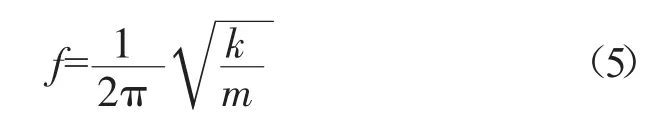
式中：f——振动频率，Hz；

k——加速度，mm/s2；

m——振幅，mm。

振动时间的计算，如式（6）所示。

式中：n——振动次数，次；

T——振动时间，s。

此次振动疲劳分析分为分析A与分析B，分别对应试验A与试验B。

本次振动疲劳分析主要分析仪表板加强管柱的钣金件，需要针对各钣金件的不同材料定义不同的E/N（应变/寿命）曲线参与计算[2]。LMSVirtual.Lab提供了一种通过材料弹性模量和抗拉强度拟合材料E/N曲线的方法，本次振动疲劳分析即采用此方法。

完成振动疲劳分析参数的定义和求解后，将已定义的振动疲劳分析工况提交计算。

5 分析结果与试验结果对比分析

分析A的振动疲劳分析结果云图，如图5a所示，分析B的振动疲劳分析结果云图，如图5b所示。

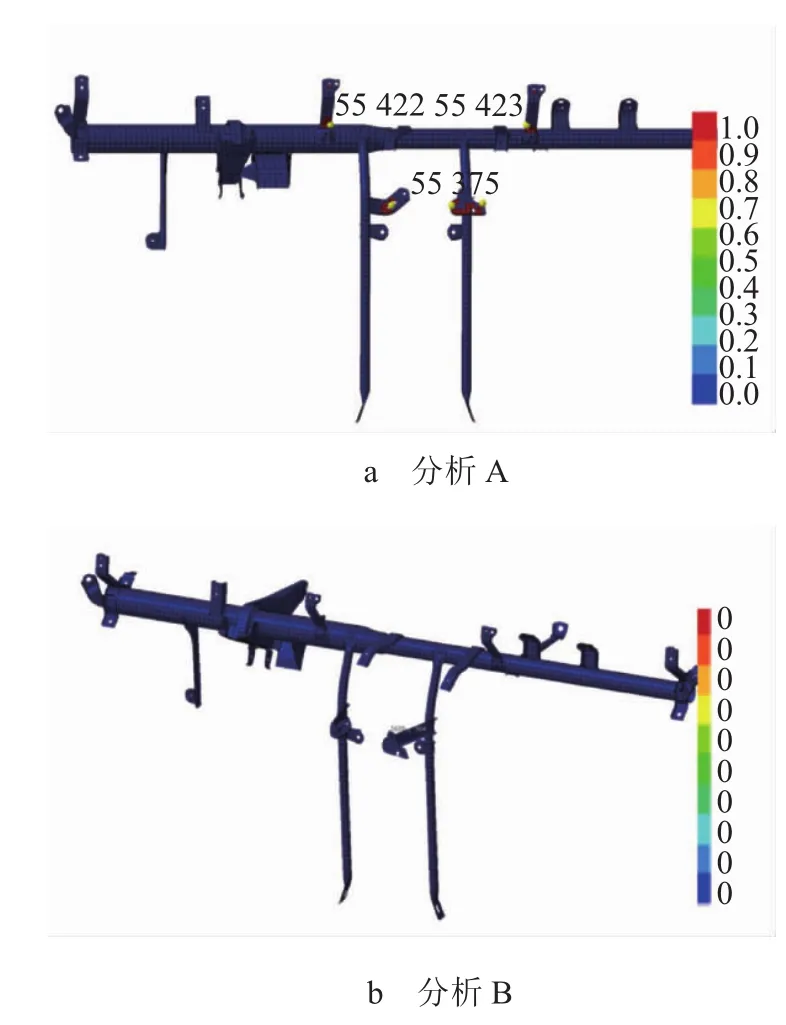
图5 加强管柱振动疲劳损伤云图

从图5a中可见，仪表板加强管柱2号支架、3号支架及收放机支架疲劳损伤均达到1（1为判定是否发生疲劳损伤的界定值），即这3处会发生疲劳破坏。与试验A结果对比，仪表板加强管柱2号支架、3号支架发生断裂与分析A的分析结果一致，收放机支架无破坏现象发生，与分析A结果存在差异。

从图5b中可见，仪表板加强管柱所有位置损伤值均未达到1，即仪表板加强管柱不存在疲劳破坏。与试验B结果对比，仪表板加强管柱无明显破坏，与分析B结果一致。

通过分析A与试验A及分析B与试验B的结果对比，证明针对汽车仪表板加强管柱分总成的振动疲劳有限元分析可以在一定程度上判定疲劳裂纹产生的位置，对产品的设计存在一定的指导作用。但是，该分析不能完全取代振动疲劳试验，零部件只有真正的通过振动疲劳试验才能证明其合格的振动疲劳性能。

6 结论

LMS Virtual Lab软件提供了一种对零部件做振动疲劳分析的途径。通过这个途径可以对处于设计阶段的零部件做振动疲劳分析，判定它们是否满足振动疲劳性能要求，从而能够及时修改，较之通过试验判定振动疲劳性能更方便快捷。但振动疲劳试验依然是不可或缺的，设计完成的零部件依然要通过振动疲劳试验来判定其振动疲劳性能，才能确保零部件设计的安全与可靠性。而振动疲劳CAE分析方法的使用，能够降低试验中产品出现振动疲劳问题的概率，减少产品返工次数从而能够缩短产品开发周期，降低产品开发成本。

本次针对汽车仪表板加强管柱的振动疲劳分析，解决了以往无法完成零部件振动疲劳性能分析的问题，为整车零部件性能优化分析打下了基础。但是本次分析结果与试验结果依然存在较大区别，说明使用线弹性有限元方法分析模态，通过LMS Virtual Lab软件做振动疲劳分析的过程中依然存在可完善之处。