深埋圆形隧洞非饱和土-衬砌结构系统的动力特性
2016-08-04刘洪波闻敏杰
刘洪波, 刘 洁 , 闻敏杰
(1. 郑州航空工业管理学院,郑州 450015,2. 嘉兴职业技术学院,浙江 嘉兴 314036)
深埋圆形隧洞非饱和土-衬砌结构系统的动力特性
刘洪波1, 刘洁1, 闻敏杰2
(1. 郑州航空工业管理学院,郑州450015,2. 嘉兴职业技术学院,浙江嘉兴314036)
采用解析方法在频率域内研究了深埋圆形隧洞非饱和土-衬砌结构系统的动力特性。基于Bishop非饱和土有效应力原理和单相流固结理论,建立了单相流条件下非饱和土的运动方程。通过位移势函数解耦,得到了非饱和土在简谐荷载作用下的动力响应解答。将衬砌结构视为均匀弹性介质,基于弹性理论,得到了简谐荷载作用下圆柱形衬砌结构的稳态形式解答。利用土体与衬砌界面的连续性条件和衬砌结构内边界上的边界条件,确定了表达式的待定系数。在此基础上,考察了饱和度、吸力折减系数、衬砌厚度等参数对非饱和土响应幅值的影响。结果表明:随着衬砌厚度的增加,系统响应幅值逐渐减小;饱和度和吸力折减系数对孔隙水压力幅值的影响较大,而对径向位移和环向应力幅值的影响较小。
非饱和土;单相流;圆柱形衬砌结构;动力特性;解析解
土体具有丰富且较为复杂的力学特性,尤其是地下结构受到爆炸、冲击等内源动力荷载作用时常导致土体发生变形,结构和土体之间时有发生扰动,由此,土体的力学性能对地铁、电力管线、污水管道和海底隧道等地下工程的安全运营具有直接的影响。近年来,国内外学者在研究具有圆形隧道周围土体的动力响应方面取得了大量成果,可用于地下隧道工程抗爆设计、稳定性分析等。这些研究或是把周围土视为单相介质[1-5],或是把周围土视为流固两相介质[6-10],分析土体的动力特性。
然而,我国隧道分布密集区都以软土的形式存在,以往的单相弹性地基模型和流固耦合两相介质模型与实际工程中常见的软土有很大差异。这些软土常为流、固、气三相介质,将土体视为单相或两相介质,不能精确地反映土体的真实特性[11]。为此,徐长节等[12-14]假定土体中气相仅以分散气泡形式存在于水中,将水气混合物视为均匀流体,采用Biot两相介质理论分别研究了具有高饱和度的准饱和弹性土和黏弹性土动力特性。但是,上述研究仅针对饱和度在95%以上的土体。为了更好地描述具有圆柱形衬砌结构非饱和土的动力行为,本文基于Bishop非饱和土有效应力原理和单相流固结理论,采用解析方法在频率域内研究了深埋圆形隧洞非饱和土-衬砌结构系统的动力特性,对比分析了无衬砌和弹性衬砌、边界透水与不透水、非饱和土与饱和土等情形下的动力响应差异,并考察了物性和几何参数对非饱和土响应幅值的影响。
1 非饱和土体的控制方程及求解过程
如图1所示,非饱和土体中有一内外半径分别为R1和R2,厚度为d=R2-R1,圆心到中曲面的距离为a的圆柱形隧洞,其内边界承受圆频率为ω的径向均布简谐激振力q0eiωt(i2=-1)。假设非饱和土-衬砌系统为小变形,且衬砌和土体完全接触,即满足位移和应力连续。不计体力时,该问题可视为轴对称平面应变问题。
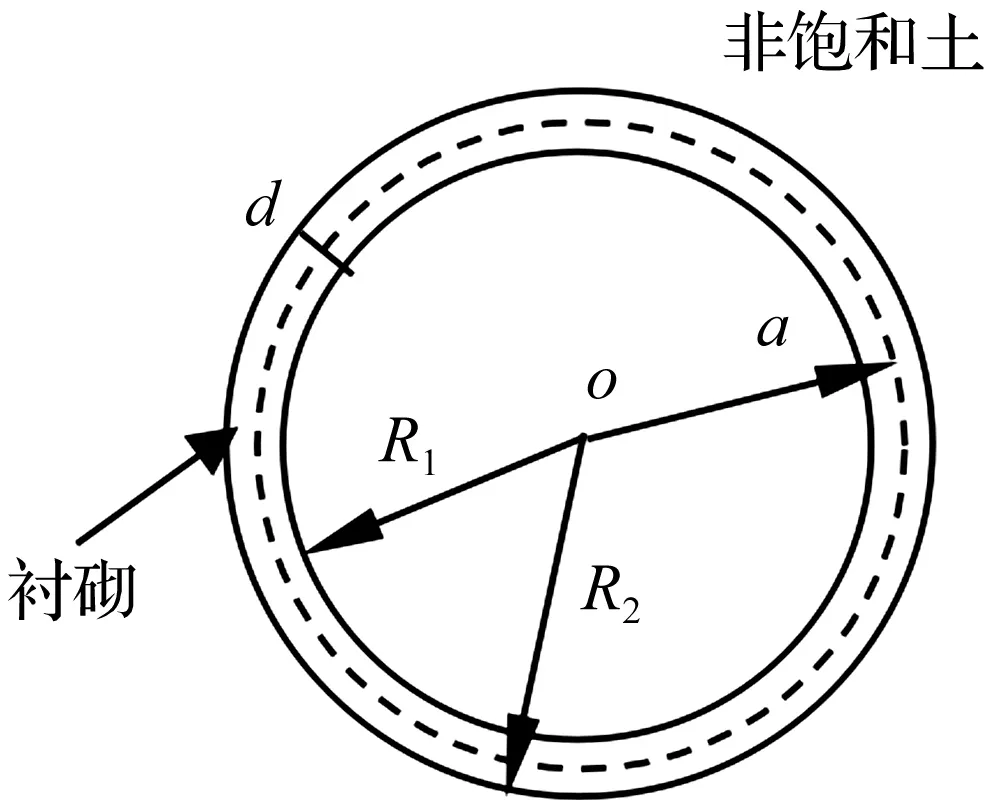
图1 非饱和土中圆形衬砌隧洞Fig.1 Circular lined tunnel in unsaturated soil
根据单相固结理论[15],非饱和土体满足单相流条件,即饱和度适中,忽略排气过程,各处气体压力均与大气压力相等,仅考虑水力梯度和吸力梯度下孔隙水的流动。因此,土体的应力关系用Bishop提出的非饱和土有效应力原理表示为:
(1)
式中:σSE,σ*,σ分别表示土体的有效应力、净应力和总应力;Sa和χ分别为吸力和吸力折减系数;pa为土体的孔隙气压力,当气体压力始终为大气压时,孔隙气压pa可取为0;{δ}={1,1,1,0,0,0}T
于是,在极坐标下土体的总应力-应变关系可表示为:
(2)
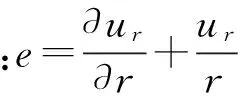
土体的运动平衡方程为:
(3)
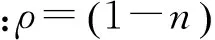
孔隙流体运动方程为:
(4)
式中:k为液体的渗透系数,而Sr为饱和度。
非饱和土中孔隙水连续方程为:
(5)
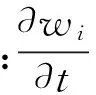
流相相对于固相的渗流速度表示为:
(6)
根据沈珠江等[15]研究成果,可知:
(7)
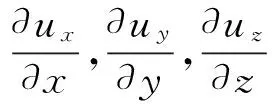
结合式(5)~(7),可得土体的孔隙水压力满足如下本构关系:
(8)
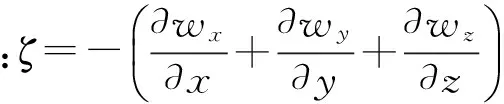
将式(2)代入式(3)和(8),式(4)代入式(8),可得:
(9)
式中:λc=λ+χαM,M=Hw/n,α=Sr(1+n),b=ρwg/k,m=ρw/nSr
对于系统作稳态振动,令p=GPeiωt,ur=R2Uηeiωt,wr=R2Wηeiωt,其中,P,Uη,Wη分别为p,ur,wr的无量纲量,并引入无量纲量和常数:
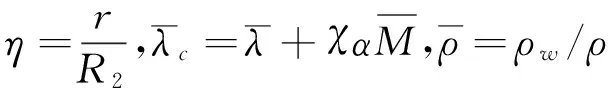
(10)
同时,利用文献[14]的解法和无穷远处位移为零的边界条件,并略去eiωt项,土体的径向位移和流体相对于土骨架的径向位移表达式分别为
(11)
利用本构关系式(8),可得孔隙水压力的表达通式为
(12)
根据关系式(2),可得土体的径向和环向总应力分别为
(13)
(14)
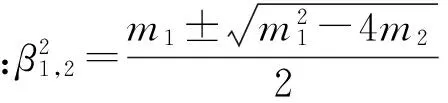
m1=
(15a)
(15b)
(16)
2 非饱和土体的控制方程及求解过程
将衬砌视为均匀弹性介质,根据弹性理论,动力荷载作用下以位移表示的运动方程为[6-7]:
(17)
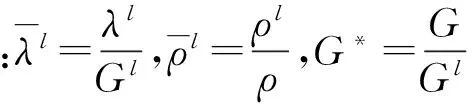
式(17)易解得:
(18)
根据应力-位移的本构关系,可得径向和环向应力分别为:
(19)
(20)
满足如下边界条件:
(21)
② 在衬砌与土体界面处,有
(22)
③ 若外边界不透水
wr=0r=R2
(23)
④ 若外边界自由透水
p=0,r=R2
(24)
将式(11)~(14)和式(18)~(20)代入式(21)~(24),易求得待定系数Ai,Di(i=1,2)的具体表达式,即可得到深埋圆形隧洞非饱和土-衬砌系统稳态振动的解析解。
3 图形分析及讨论
据文献[13-14]取值如下:
η=1,γ=d/R2=0.005,n=0.4,
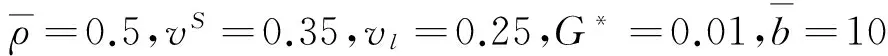
(25)
3.1对比分析
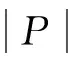


(a) 径向位移随频率变化(a) 环向应力随频率变化(a) 孔隙水压力随频率变化(a) 孔隙水压力随频率变化


(b) 径向位移随半径变化图2 有无衬砌时径向位移幅值的比较Fig.2Comparisonoftheamplitudeoftheradialdisplacementwithorwithoutlining(b) 环向应力随半径变化图3 有无衬砌时环向应力幅值的比较Fig.3Comparisonoftheamplitudeofthehoopstresswithorwithoutlining(b) 孔隙水压力随半径变化图4 有无衬砌时孔隙水压力幅值的比较Fig.4Comparisonoftheamplitudeoftheporewaterpressurewithorwithoutlining(b) 孔隙水压力随半径变化图5 透水情形下孔隙水压力幅值Fig.5Theamplitudeoftheporewaterpressureforpermeablecondition
3.2饱和度的影响
3.3吸力折减系数的影响
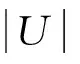
3.4衬砌厚度的影响


(a) 径向位移随频率变化(a) 环向应力随频率变化(a) 孔隙水压力随频率变化(a) 径向位移随频率变化


(b) 径向位移随半径变化图6 饱和度对径向位移幅值的影响Fig.6Influenceofsaturationontheamplitudeofradialdisplacement(b) 环向应力随半径变化图7 饱和度对环向应力幅值的影响Fig.7Influenceofsaturationontheamplitudeofthehoopstress(b) 孔隙水压力随半径变化图8 饱和度对孔隙水压力幅值的影响Fig.8Influenceofsaturationontheamplitudeoftheporewaterpressure(b) 径向位移随半径变化图9 透水情形下饱和度对径向位移幅值的影响Fig.9Influenceofsaturationontheamplitudeofradialdisplacementforpermeablecondition


(a) 径向位移随频率变化(a) 环向应力随频率变化(a) 孔隙水压力随频率变化(a) 径向位移随频率变化


(b) 径向位移随半径变化图10 吸力折减系数对径向位移幅值的影响Fig.10Influenceofreductioncoefficientofsuctionontheamplitudeoftheradialdisplacement(b) 环向应力随半径变化图11 吸力折减系数对环向应力幅值的影响Fig.11Influenceofreductioncoefficientofsuctionontheamplitudeofthehoopstress(b) 孔隙水压力随半径变化图12 吸力折减系数对孔隙水压力幅值的影响Fig.12Influenceofreductioncoefficientofsuctionontheamplitudeoftheporewaterpress(b) 径向位移随半径变化图13 衬砌厚度对径向位移幅值的影响Fig.13Influenceofliningthicknessontheamplitudeoftheradialdisplacement


(a) 环向应力随频率变化(b) 环向应力随半径变化(a) 孔隙水压力随频率变化(b) 孔隙水压力随半径变化图14 衬砌厚度对环向应力幅值的影响Fig.14Influenceofliningthicknessontheamplitudeofthehoopstress图15 衬砌厚度对孔隙水压力幅值的影响Fig.15Influenceofliningthicknessontheamplitudeoftheporewaterpressure
4 结 论
基于单相流固结理论和Bishop非饱和土有效应力原理,采用解析方法在频率域内研究了深埋圆形隧洞非饱和土-衬砌结构系统的动力特性,并对比了无衬砌和弹性衬砌两种条件下非饱和土的动力特性差异,得到以下结论:
(1) 有弹性衬砌时非饱和土的径向位移幅值明显小于无弹性衬砌的,且随着衬砌厚度γ的增加,系统响应幅值逐渐减小。适当增加衬砌厚度γ可避免系统的共振。
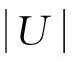
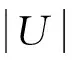
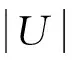
[1] Forrestal M L, Sagartz M J. Radiated pressure in an acoustic medium produced by pulsed cylindrical and spherical shells[J]. AMSE Journal of Applied Mechanics, 1971,38:1057-1060.
[2] Zakout U, Akkas N. Transient response of a cylindrical cavity with or without a boned shell in infinite elatic medium[J]. International Journal of Engineering Science, 1997, 35(12/13): 1203-1220.
[3] Seyyed M, Hasheminejad Mojtaba K. Effect of imperfect bonding on axisymmetric elastodynamic resonpose of a lined circular tunnel in poroelastic soil due to a moving ring load[J]. International Journal of Solids and Structures, 2009, 46: 398-411.
[4] Gao M, Wang Y, Gao G Y. Dynamic response of cylindrical lined cavity in elastic medium[J]. Journal ofCentral South University, 2013, 20(10): 2849-2855.
[5] 姚署霖, 闻敏杰. 黏弹性土中衬砌隧道振动响应的解析解[J]. 工程力学, 2014, 31(3): 109-115.
YAO Shu-lin, WEN Min-jie.Analytical solutions of dynamic responses of lined tunnel in viscoelastic soil[J]. Engineering Mechanics, 2014, 31(3): 109-115.
[6] 高华喜, 闻敏杰. 内水压力作用下黏弹性饱和土-隧洞衬砌相互作用[J]. 工程力学, 2013, 30(3): 289-296.
GAO Hua-xi, WEN Min-jie.Interaction of viscoelastic saturated soil and tunnel lining subject to inner water pressure[J]. Engineering Mechanics, 2013, 30(3): 289-296.
[7] 杨骁, 闻敏杰. 饱和分数导数型黏弹性土-深埋圆形隧洞衬砌系统的动力特性[J].工程力学,2012,29(12):248-255.
YANG Xiao, WEN Min-jie.Dynamic characteristics of saturated fractional derivative type viscoelastic soil and lining system with a deeply embedded circular tunnel[J]. Engineering Mechanics, 2012, 29(12): 248-255.
[8] 高盟, 高广运, 李大勇. 考虑耦合质量影响的均布突加荷载作用下衬砌结构的瞬态响应[J]. 岩土工程学报, 2011, 33(6): 862-868.
GAO Meng, GAO Guang-yun, LI Da-yong.Transient response of lining structure subjected to sudden internal uniform loading considering effects of coupling mass[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(6): 862-868.
[9] 高盟, 高广运. 饱和地基任意形状衬砌内部均布突加荷载作用下的动力响应[J]. 固体力学学报, 2011, 32(6): 655-664.
GAO Meng, GAO Guang-yun.Dynamic response of lining in saturated foundation subjected to sudden internal uniform loading[J]. Chinese Journal of Solid Mechanics,2011,32(6):655-664.
[10] 蔡袁强, 陈成振, 孙宏磊. 爆炸荷载作用下饱和土中隧道的瞬态动力响应[J]. 岩土工程学报,2011,33(3):361-367.
CAI Yuan-qiang, CHEN Cheng-zhen, SUN Hong-lei. Transient dynamic response of tunnels sujected to blast loads in saturated soil[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(3): 361-367.
[11] 张智卿, 王奎华, 李强, 等. 非饱和土中端承桩纵向振动问题简化解[J]. 工程力学, 2010, 27(5): 159-165.
ZHANG Zhi-qing, WANG Kui-hua, LI Qiang, et al. Simplified solution for vertical vibration of an end bearing pile embedded in unsturated soil[J]. Engineering Mechanics, 2010, 27(5): 159-166.
[12] 徐长节,马晓华,蔡袁强. 弹性准饱和土中球空腔的动力响应[J]. 岩土工程学报,2005,27(8): 934-938.
XU Chang-jie, MA Xiao-hua, CAI Yuan-qiang. Dynamic response of spherical cavity in nearly saturated elastic soils[J]. Chinese Journal of Geotechnical Engineering, 2005,27(8): 934-938.
[13] 高华喜, 闻敏杰. 准饱和黏弹性土-隧道衬砌系统的动力特性[J]. 工程力学, 2013, 30(5): 90-96.
GAO Hua-xi, WEN Min-jie.Dynamic characteristics of nearly saturated viscoelastic soil and lining system with a tunnel[J]. Engineering Mechanics, 2013, 30(5): 90-96.
[14] 高华喜, 闻敏杰, 张斌. 具有圆形隧道的准饱和黏弹性土振动响应[J]. 浙江大学学报:工学版,2013,47(4):615-621.
GAO Hua-xi, WEN Min-jie, ZHANG Bin. Dynamic responses of nearly saturated viscoelastic soil with a deeply embedded circular tunnel[J]. Journal of Zhejiang University:Engineering Science, 2013, 47(4): 615-621.
[15] 沈珠江. 理论土力学[M]. 北京: 中国水利水电出版社, 2000.
Dynamic characteristics of an unsaturated soil and lining structure system with a deeply embedded circular tunnel
LIU Hong-bo1, LIU Jie1, WEN Min-jie2
(1. Zhengzhou Institute of Aeronautical Industry Management, Zhengzhou 450015, China; 2. Jiaxing Vocational Technical College, Jiaxing 314036, China)
Using the analytical method, the dynamic characteristics of an unsaturated soil and lining structure system with a deeply embedded circular tunnel were studied in frequency domain. Based on Bishop’s effective stress principle and one-phase flow consolidation theory, the motion equations of unsaturated soil subjected to one-phase flow were established. An analytical solution to the dynamic response of unsaturated soil subjected to harmonic load was obtained by means of the displacement potential function. The lining structure was treated as a homogeneous elastic medium. Based on the elastic theory, the steady-state dynamic response of a cylinder lining structure subjected to harmonic load was obtained. By utilizing the inner boundary condition of the lining structure and the continuity conditions between soil and lining, the unknown coefficients in the expressions were determined. Then, the effects of saturation, suction reduction coefficient and lining thickness on response amplitudes of unsaturated soil were investigated. It was shown that the response amplitudes of the system decrease gradually with increase in lining thickness; the saturation and suction reduction coefficient have a larger effect on the amplitudes of pore water press, while their effects on the amplitudes of radial displacement and hoop stress are smaller.
unsaturated soil; one-phase flow; cylinder lining structure; dynamic characteristics; analytical solution
10.13465/j.cnki.jvs.2016.13.007
国家自然科学基金(51508524);河南省科技攻关项目(112102310633);浙江省自然科学基金项目(LY12E09006)
2015-06-23修改稿收到日期:2015-09-17
刘洪波 男,博士,副教授,1975年生
闻敏杰 男,博士生,讲师,1986年生
E-mail: 7279026@163.com
TU435
A
