双向水平地震下7度区框架结构的“强柱弱梁”措施
2016-08-04任小军白绍良
杨 红, 任小军, 白绍良
(1.重庆大学 土木工程学院,重庆 400045;2.重庆大学 山地城镇建设与新技术教育部重点实验室, 重庆 400045;3. 中煤国际工程集团重庆设计研究院,重庆 400016)
双向水平地震下7度区框架结构的“强柱弱梁”措施
杨红1, 2, 任小军3, 白绍良1, 2
(1.重庆大学 土木工程学院,重庆400045;2.重庆大学 山地城镇建设与新技术教育部重点实验室, 重庆400045;3. 中煤国际工程集团重庆设计研究院,重庆400016)
结合汶川地震中钢筋混凝土框架结构的塑性铰普遍出现在柱端的震害现象,重点研究了“强柱弱梁”措施和“超烈度”对结构抗震性态的影响。按中国规范分别设计7度0.1 g区和0.15 g区三级抗震规则空间框架,并采用逐渐增大的“强柱弱梁”措施,对两类7度区框架各形成5个算例结构。在OpenSees平台上,计算框架在双向水平地震作用下的非线性反应。结果表明,抗震规范GB50011-2001给出的三级抗震的“强柱弱梁”措施取值明显偏低,在罕遇地震作用下7度0.1 g区框架塑性铰数量少、基本为柱铰,7度0.15 g区框架塑性铰数量较多、梁铰少。抗震规范GB50011-2010提高柱端弯矩增大系数取值后,结构的塑性铰分布规律基本没有改善。按抗震规范GB50011-2001设计的7度区空间框架在“超烈度”地震波作用下的损伤特征是塑性铰普遍出现在柱端,与汶川地震的震害现象一致,7度区框架的梁端地震组合弯矩小、现浇板钢筋影响幅度大、“强柱弱梁”措施过低、结构遭遇“超烈度”共同导致了该危险的塑性铰分布特征。
钢筋混凝土;三维框架;双向水平地震作用;强柱弱梁;非线性分析
“能力设计”(Capacity Design)方法的核心思想是使钢筋混凝土结构能够在设计地震作用取值较低的情况下,通过脆性破坏防止措施、延性性能保障措施以实现强烈地震作用下的设防目标。其中,“强柱弱梁”措施是引导框架结构在强震下形成合理的塑性铰耗能机制、提高延性性能的关键,已为世界各国结构设计规范广泛采用。我国《建筑抗震设计规范》GB50011-2010[1](简称抗规2010)第6.2.2条给出的柱端弯矩增强措施的一般形式为:
∑Mc≥ηc∑Mb
(1)
式(1)中:ηc为柱端弯矩增大系数,对一、二、三、四级框架结构分别取1.7、1.5、1.3和1.2;∑Mc为节点上下柱端截面顺时针或反时针方向组合的弯矩设计值之和;∑Mb为节点左右梁端截面反时针或顺时针方向组合的弯矩设计值之和,对一级框架当节点左右梁端均为负弯矩时,绝对值较小的负弯矩取为零。
抗规2010[1]将二级抗震的ηc取值由《建筑抗震设计规范》GB50011-2001[2](简称抗规2001)的1.2提高至1.5,对单向地震输入下的平面框架而言,ηc取1.5对塑性铰的控制效果已较为理想[3],不足之处是双向水平地震输入下空间框架在罕遇地震作用下出现了同一楼层全部柱端形成塑性铰的现象[4]。对在我国应用范围更广泛的三级抗震框架结构,ηc的取值由抗规2001[2]的1.1提高至抗规2010的1.3[1],其确定方法仍沿用我国抗震规范的长期习惯,即ηc取值随抗震等级降低而逐级减小,但ηc取1.3对7度区框架抗震性态的控制效果目前尚不明确,其取值依据并不充分。
研究表明[5],7度0.1 g区和0.15 g区三级抗震框架由于中间节点左、右梁端地震组合弯矩设计值Mb均为负弯矩的情况较为普遍,将导致∑Mb较小,且现浇楼板的影响幅度更大,故使得7度0.1 g区和0.15 g区框架在大震下保持柱纵筋不屈服所需的柱端弯矩增大系数计算结果高至2.3~3.0,该结果比高烈度区明显更大。其原因在于,高烈度区框架中间节点左、右梁端Mb一般分别为正、负,计算∑Mb时左、右梁端弯矩相当于绝对值相加,且楼板钢筋的影响幅度更小(其梁端配筋更多)。可见,若把在罕遇地震下将塑性铰分布控制在大致相同的程度作为各烈度区框架共同的抗震设防目标,对7度区三级框架而言,取ηc等于1.3实现上述共同设防目标的难度从理论上看将比高烈度区框架明显更大。此外,7度区框架的柱纵筋由最小配筋率ρmin控制的情况较多,这相当于间接提高了部分柱端的ηc取值,但ρmin对ηc的有利影响难以直接定量。因此,7度区框架的抗震性态控制效果取决于上述不利、有利影响因素的综合,目前尚缺乏直接的计算验证结果,ηc的合理取值仍有待研究。
2008年之前,受汶川地震影响较严重的地区多为7度0.1 g区(都江堰、汶川、北川、绵竹、什邡、江油等)和7度0.15 g区(茂县、平武等)。汶川地震中,这些按三级抗震设计的钢筋混凝土多层框架结构普遍出现了柱端塑性铰,甚至形成“柱铰机制”的震害现象引起了我国结构工程界的重视,一些学者讨论了现浇楼板、填充墙、框架梁端超配筋等的影响[6-7],但并未结合7度区框架的配筋特点进行分析。此外,结构设计时梁惯性矩增大系数的取值方法、柱线刚度取值偏小的影响也有待进一步分析。文献[8]研究了抗规2001[2]的ηc取值对不同烈度区、抗震等级空间框架的塑性铰控制效果,仍缺乏抗规2010的ηc取值与7度区框架震害现象的相关性。综上可见,我国现行抗规2010[1]的ηc取值对7度区框架塑性铰的控制效果,以及7度区框架更为合理的“强柱弱梁”措施有待澄清。
本文按抗规2001[2]、抗规2010[1]分别设计7度0.1 g区和0.15 g区空间框架,通过逐渐变化上部各层柱端、底层柱下端的弯矩增大系数,各形成5个典型算例,然后以双向水平地震输入下的非线性动力反应分析结果和性态评估为依据,分析7度0.1 g区和0.15 g区三级抗震框架结构分别采用不同“强柱弱梁”措施时的抗震效果。最后,对7度区框架在“超烈度”下的非线性反应进行计算,分析了ηc取值、“超烈度”等对柱端塑性铰的影响规律。
1 框架的基本信息及“强柱弱梁”措施取值
算例空间框架为均匀、规则的丙类办公建筑,其平面布置见图1。框架共八层,底层层高为4.2 m,其它层为3.0 m。框架分别按7度0.1 g区、0.15 g区的第一设计分组、Ⅱ类场地进行抗震设计。
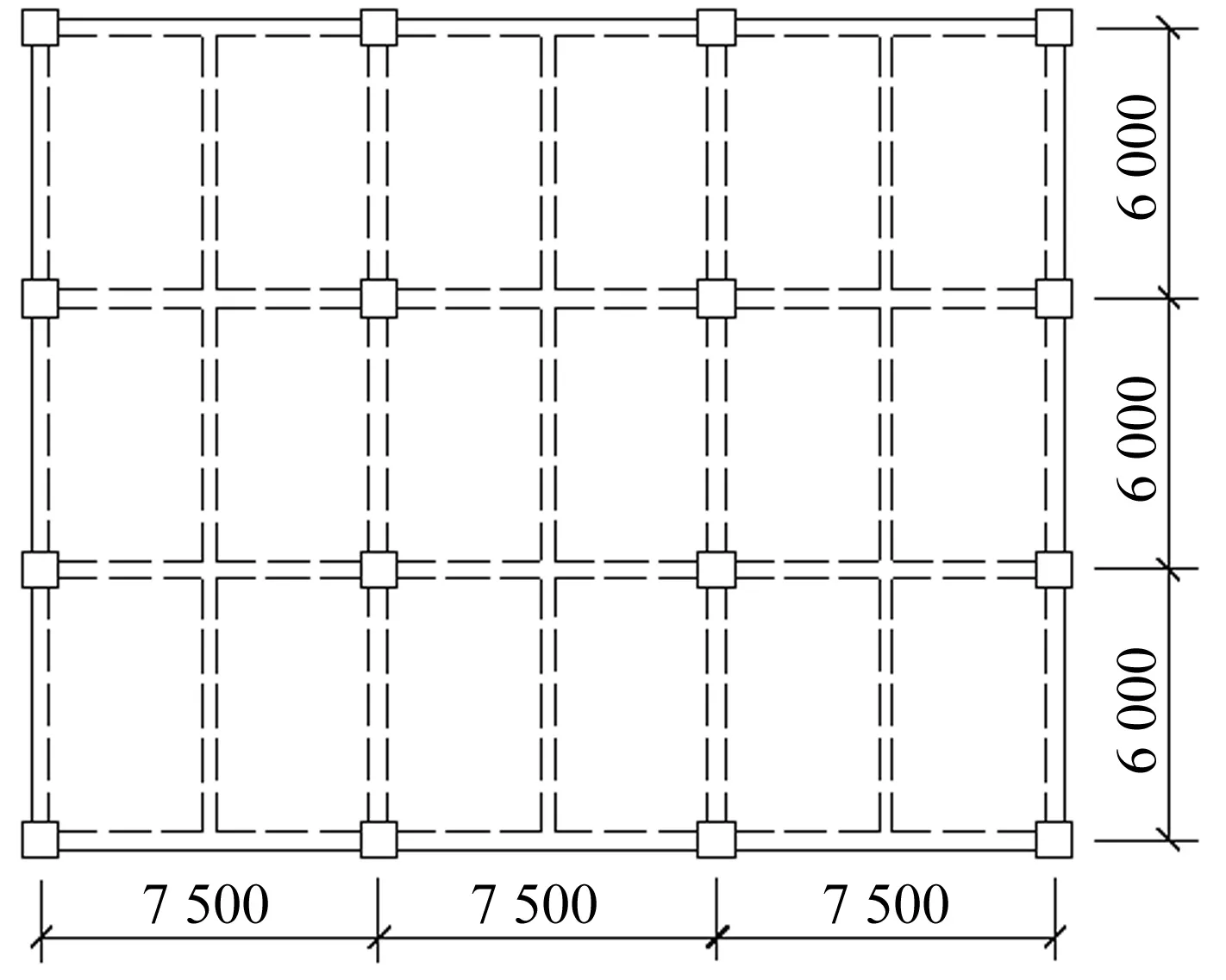
图1 空间框架的平面布置图(单位:mm)Fig.1 Plan view of the spatial frame(Unit:mm)
两类空间框架抗震等级均为三级,柱、梁、楼板混凝土强度等级皆为C30。为了使算例框架的配筋符合2008年之前的工程设计习惯,柱、梁纵筋分别采用HRB335、HRB400级钢筋,楼板钢筋和箍筋采用HRB235级钢筋。楼面、屋面现浇板厚分别为100 mm、120 mm,框架梁、次梁截面尺寸分别为300 mm×700 mm、200 mm×600 mm。0.1 g区框架的中柱、边柱(包括角柱)截面尺寸分别为550 mm×500 mm、450 mm×450 mm;0.15g区的中柱、边柱(角柱)分别为550 mm×500 mm、500 mm×450 mm。0.1 g区、0.15 g区空间框架的基本周期分别为1.15 s、1.13 s。
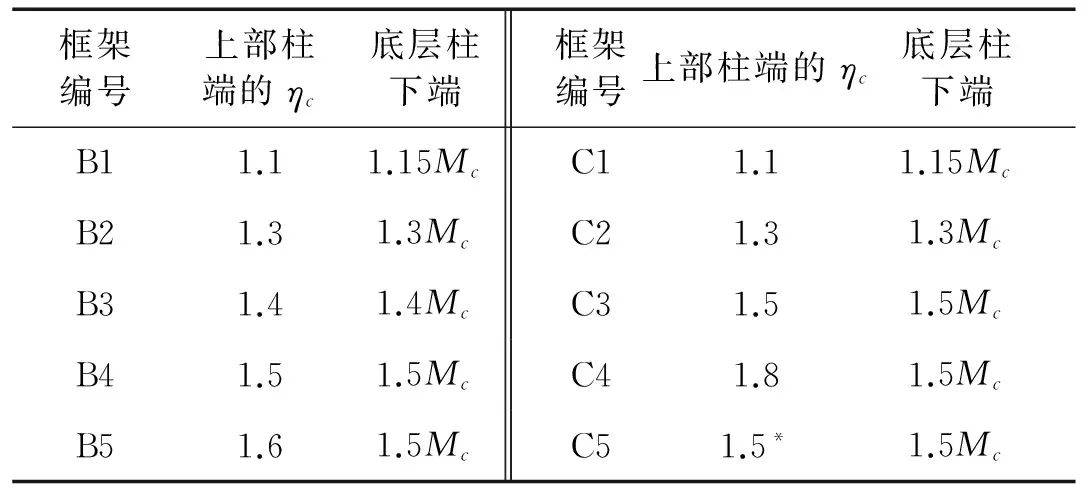
表1 各空间框架选用的“强柱弱梁”措施
注:表中“上部柱端的ηc”用于表达式∑Μc=ηc∑Μb;框架C5的“上部柱端的ηc”(表中带*号的数)用于表达式∑Μc=ηc∑Μbua,其中Μbua为根据实配钢筋面积(计入受压筋)和材料强度标准值计算的梁端正截面抗震受弯承载力所对应的弯矩值。
各框架的楼面恒载、活载分别为4.0 kN/m2、3.17 kN/m2(其中包括将非固定轻质隔墙等效为每延米取1/3轻质隔墙的重量作为楼面活载附加值);屋面恒载、活载分别为6.84 kN/m2、2.0 kN/m2;楼面固定隔墙8.2 kN/m(布置在周边)、屋面女儿墙3.5 kN/m。
按《混凝土结构设计规范》GB50010-2010[9]进行结构设计时,梁、柱截面钢筋面积尽可能不人为增大。框架采用SAP2000软件进行内力分析,内力组合、“强柱弱梁”等内力调整和配筋计算均人工完成,其中柱配筋分别按表1给出的“强柱弱梁”措施确定,从而形成7度0.1 g区框架共5个(B1~B5,5个框架仅柱配筋不同)、7度0.15 g区框架5个(C1~C5,仅柱配筋不同)。
如表1所示,将按抗规2001要求的“强柱弱梁”措施确定柱配筋所得到的空间框架编号为B1或C1,其底层柱下端的弯矩增大系数为1.15、上部各柱端的ηc为1.1;将按抗规2010的“强柱弱梁”措施得到的空间框架编号为B2或C2,其底层柱下端的弯矩增大系数、上部各柱端的ηc皆取1.3。
7度0.1 g区和0.15 g区各空间框架的梁、柱配筋特点是:两类框架的梁端上部钢筋皆由地震作用参与的组合弯矩控制,梁端下部钢筋大部分由跨中弯矩控制;0.1 g区框架B1和B2的柱配筋除底层柱外,其它大部分由ρmin控制;0.15 g区框架C1、C2也是大部分柱(数量相对0.1 g区框架更少)的配筋由ρmin控制。
2 结构模型化方法及双向地震动输入
所有非线性反应分析均在OpenSees[10]平台中完成。建立有限元模型时,单元对象均采用基于柔度法的非线性梁柱单元(Force Based Nonlinear Beam Column Element),梁、柱分别设置5个、4个积分点,框架梁考虑左、右梁侧各6倍现浇板厚度的翼缘(包括楼板钢筋),形成T形或倒L形截面。材料对象中,混凝土均采用Concrete01 Material单轴材料,并按Kent-Park[11]无约束混凝土模型、Scoot-Kent-Park[12]约束混凝土模型分别确定保护层(包括梁侧现浇板)、核心区混凝土的骨架曲线各特征点取值,各特征点参数的具体计算方法可参见文献[13]。钢筋纤维采用Steel02 Material单轴材料,该修正Menegotto-Pinto模型[14]可考虑Bauschinger效应等,钢筋材料模型的fy取其屈服强度平均值,其它参数的确定方法参见文献[13]。
按照抗规2010[1]和文献[15]建议的选波方法,对0.1 g区和0.15 g区各选取7组地震波,见表2。表中“峰值比”是沿结构两个主轴方向分别输入不同地震波分量时,两方向峰值加速度的比值,本文按实际记录取值;PGA是较大分量的地面运动峰值加速度。对各框架在罕遇地震作用下进行分析时,各地震波较大分量的峰值加速度按抗震规范[1]第5.1.2条的规定确定,即7度0.1 g区取220 cm/s2,7度0.15 g区取310 cm/s2,较小分量的峰值则按实际峰值比(见表2)确定。
3 罕遇地震作用下的分析结果和评价
框架B1~B5和C1~C5的计算结果表明,地震波较大分量分别沿X轴输入、沿Y轴输入时,结构地震反应的基本规律类似。限于篇幅,以下均以较大地震波分量沿X向输入所得结果为例进行分析。
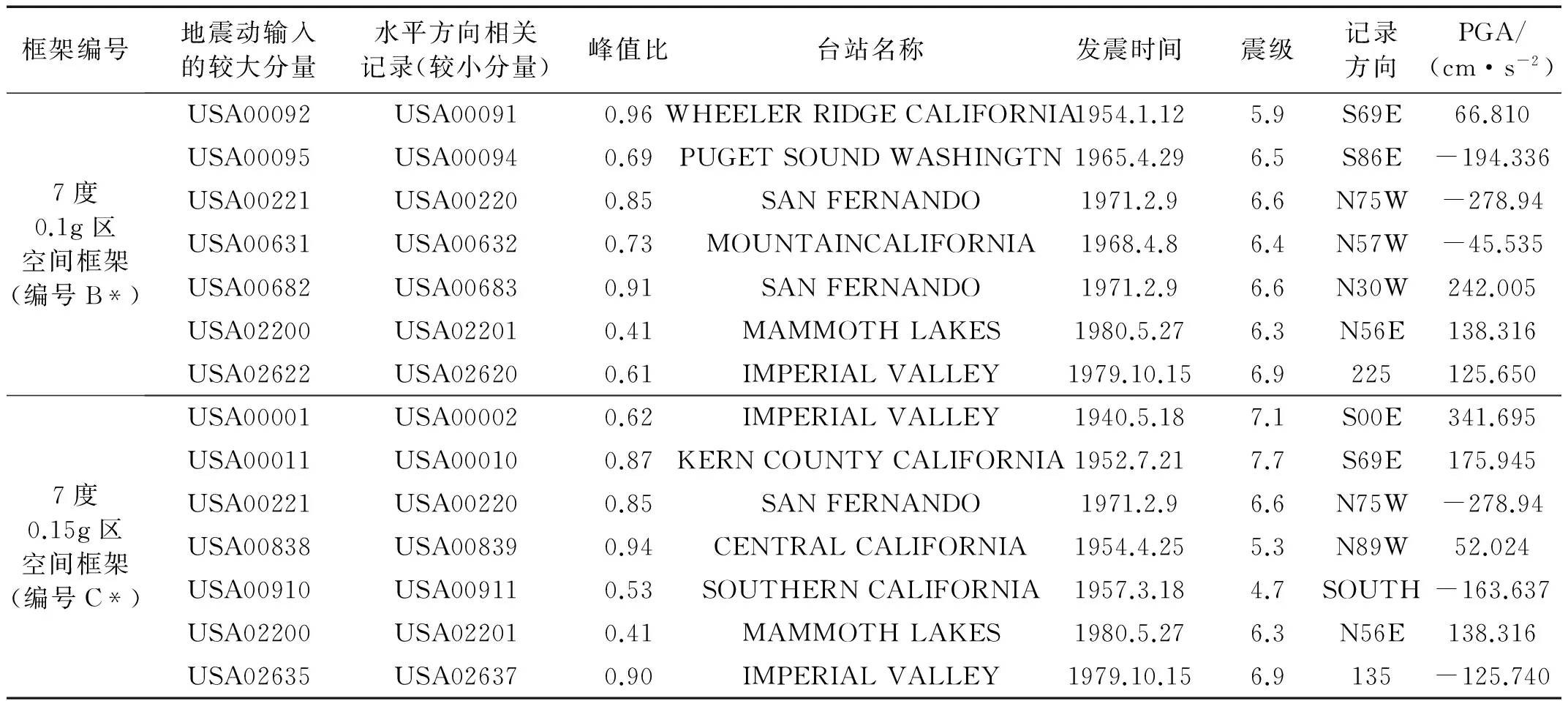
表2 输入地震波的基本信息
3.1最大位移反应和最大纤维应变
表3所示为各框架的最大顶点位移、X轴方向最大层间位移角在7组双向地震波输入下的最大值、平均值(下同)。结果表明,框架B1~B5最大顶点位移的平均值、最大值变化较小;X轴方向最大层间位移角的最大值逐渐从1/91(框架B1)减小为1/150左右(B4和B5)、平均值变化相对更小,这是由于在USA02622波作用下各框架最大层间位移角明显比其它地震波作用下的反应更大所导致。对7度0.15 g区框架而言,除C1外,C2~C5的最大顶点位移变化较小;X轴方向最大层间位移角的最大值(均为USA00011波作用下的反应)、平均值均随“强柱弱梁”措施增强而逐渐减小。可见,随着“强柱弱梁”措施逐渐增强(柱配筋从B1或C1逐渐增大为B5或C5),各框架的整体位移反应变化较小,但USA02622波作用下7度0.1 g区框架、USA00011等波作用下7度0.15 g区框架的塑性变形在局部楼层集中的现象得到了一定改善。

表3 最大顶点位移和X轴方向最大层间位移角
表4为空间框架各杆端截面混凝土纤维、钢筋纤维在7组地震波输入下的最大应变的最大值、平均值。由表4可发现,随着“强柱弱梁”措施增强,柱端混凝土纤维、钢筋纤维的最大应变明显减小,其中B4与B5的柱端纤维最大应变相近,其与B1、B2的柱端纤维最大应变差别相对较大,这表明提高“强柱弱梁”措施可减小柱端纤维最大应变,但“强柱弱梁”措施增强到一定幅度后其效率降低。对7度0.15 g区框架而言,随着“强柱弱梁”措施从C1提高至C4,柱端纤维最大应变明显减小,但其减小幅度降低;C5的柱端钢筋纤维最大应变较C4稍大,表明∑Mc=1.8∑Mb的“强柱弱梁”措施对空间框架杆端塑性变形的控制效果略好于∑Mc
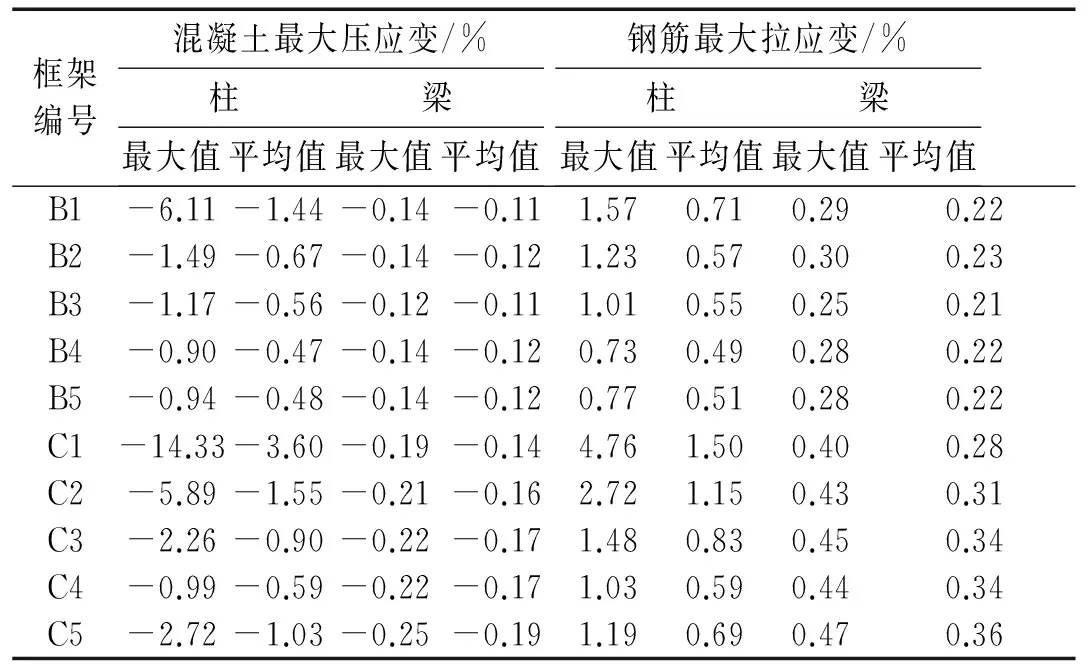
表4 混凝土纤维、钢筋纤维的最大应变
=1.5∑Mbua。对7度0.1 g区框架、0.15 g区框架而言,梁端混凝土纤维、钢筋纤维最大应变随“强柱弱梁”措施增强变化均很小,这表明不论框架整体的非线性程度不显著(0.1 g区框架)或较显著(0.15 g区框架),随着“强柱弱梁”措施增强,梁端非线性程度并不随柱端非线性程度的逐渐减轻而不断加深。
3.2塑性铰分布特征
表5给出了各空间框架的杆端出铰率(7组地震波输入下的最大值、平均值)以及杆端转角延性的较大需求和最大需求。其中,“较大需求”的计算方法是:在每一组双向地震波输入下将柱端或梁端的转角延性系数按照从大到小排序,并从最大值开始向后共取30%的梁或柱总数,然后分别计算其延性系数平均值,最后找出7组地震波输入下的最大值;“最大需求”则是先求出每一组双向地震波输入下梁端、柱端的最大转角延性,然后再得到7组地震波输入的最大值。
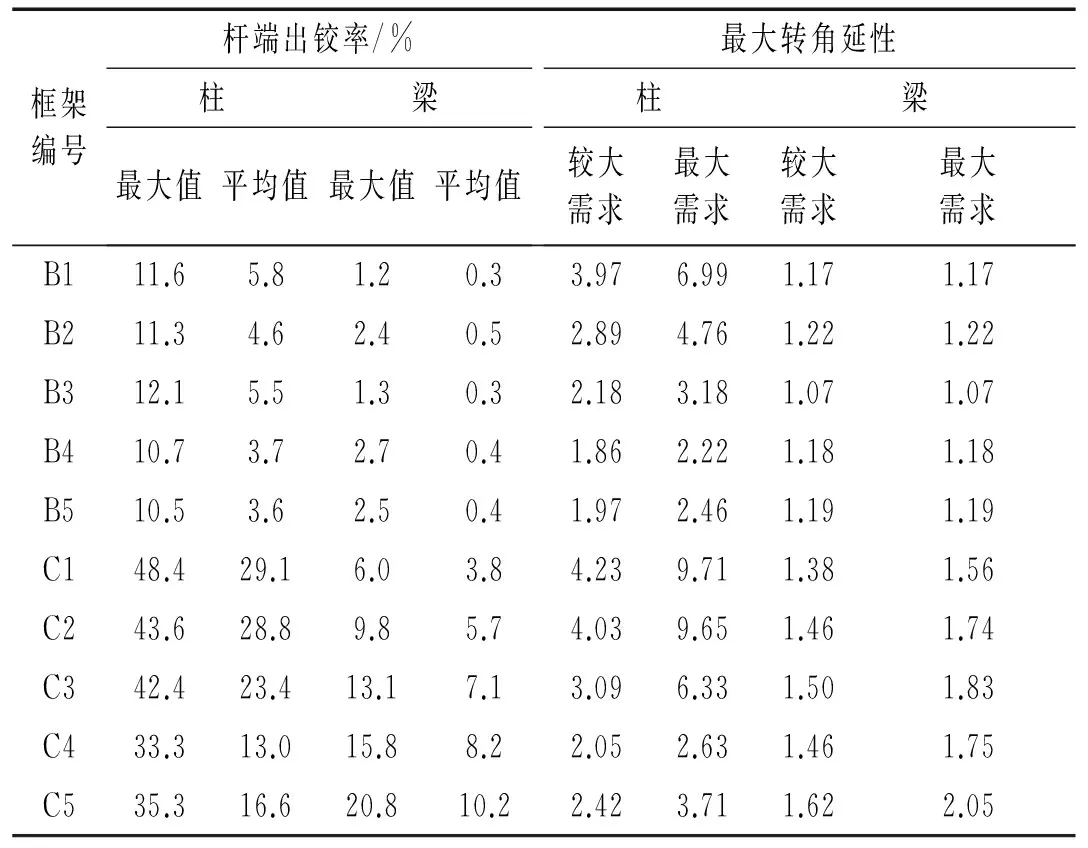
表5 杆端出铰率、最大转角延性
注: “杆端出铰率”表示发生屈服(双向屈服按两次计)的梁端(或柱端)数量与总梁端(或柱端)截面数量(每个截面按正、负向计)之比。
表5所示结果说明:
① 在抗规2001的三级抗震的“强柱弱梁”措施(ηc=1.1)控制下,框架B1柱端塑性铰数量少、塑性转动较大,梁铰极少(塑性转动也很小);框架C1柱铰非常普遍、且塑性转动过大,梁铰数量很少、塑性转动小;
② 框架B2和C2(与抗规2010对应,ηc=1.3)的塑性铰控制效果与B1、C1相比改善程度很小,较明显的变化是B2的柱端转角延性有所减小;
③ 框架B3(ηc=1.4)、C3(ηc=1.5)的柱端塑性铰数量仍变化很小,但柱端转角延性需求有一定改善;
④ 将“强柱弱梁”措施增强至ηc=1.5(框架B4)、ηc=1.8(框架C4)后,除柱端塑性铰数量有所减小外,柱端转角延性需求已基本控制在合理值范围;
⑤ 框架B5(ηc=1.6)的塑性铰控制效果与B4相比差别很小,表明继续加强“强柱弱梁”措施的效率开始下降;
⑥ 由于框架C4采用较强“强柱弱梁”措施(ηc=1.8)后塑性铰控制效果仍不理想,故C5改为依据∑Mbua进行“强柱弱梁”增强,计算结果表明C5的柱端塑性变形与框架C4相近。
图2、图3为各空间框架在7组双向水平地震波输入下的偏不利塑性铰分布。图中圆圈表示该杆端已进入屈服后状态(实心圆圈代表双向屈服,空心圆圈代表单向屈服),圆圈的大小(见图例)表示在整个时程中各杆端塑性铰曾经达到的最大弹塑性转角。
图2表明,7度0.1 g区框架B1在大震下基本只形成柱端塑性铰,梁铰极少,且柱铰位于同一楼层,有形成层侧移的风险;框架B2的塑性铰分布特征与B1类似。此外,框架B1、B2在USA00221波作用下有类似特征,其柱端塑性铰集中分布在5、6层。可见,7度0.1g区框架B1在罕遇地震下基本是柱端出现塑性铰,表明梁端抗弯承载力相对柱端而言总体上反而更强,即抗规2001的三级抗震“强柱弱梁”措施无法有效增强7度0.1 g区框架的柱端抗弯承载力;抗规2010将ηc提高为1.3(框架B2)基本没有改善效果。结合后文“超烈度”下的计算结果分析,框架B1、B2的柱端塑性铰数量不多的原因是其罕遇烈度的PGA较小。
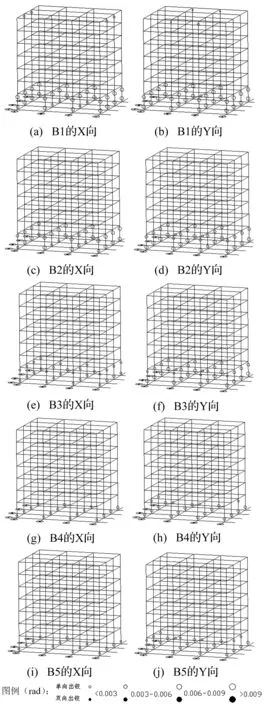
图2 USA02622波作用下7度0.1 g区框架的塑性铰分布Fig. 2 Plastic hinges distributions of 7 earthquake intensity 0.1 g region frames under USA02622 wave
框架B3除柱端塑性铰转角有一定减小外,其塑性铰特征与B1、B2类似(USA00221波作用下的反应也类似),表明ηc取1.4仍然没有明显改善效果。
框架B4、B5避免了USA02622波作用下同一楼层全部柱端出现塑性铰,但USA00221波作用下B4的第5层仍有层侧移的潜在风险(第6层仅4个柱端未出铰),其塑性铰分布特征仍是柱端出铰多、梁铰很少。可以推测,如果PGA增大(如遭遇“超烈度”),框架B4、B5将在柱端形成更多塑性铰。
图3所示塑性铰分布表明,7度0.15 g区框架C1在罕遇地震下仍然是柱铰很多、梁铰极少,且同一楼层全部柱端皆出铰的现象较为严重(例如USA00011波作用下的3、4层,USA00001波作用下的1、4、5层,USA00221波和USA02635波作用下的1、5、6层),形成“层侧移柱铰机制”的风险明显增大。
框架C2的塑性铰分布特征与C1类似,但其柱端转角略有减小、有层侧移风险的部位有所减少(USA00011波作用下的3、4层,USA00221波和USA02635波作用下的5、6层)。
上述结果表明,抗规2001的三级抗震“强柱弱梁”措施对7度0.15 g区框架(C1)的塑性铰控制效果很差,按抗规2010增加至框架C2后改善幅度很小,其根源在于,因大部分柱的纵筋由ρmin控制,框架C1、C2的柱配筋差别不大。
与C2相比,框架C3的塑性铰特征仍相似,虽然柱铰转角有一定减小,但在部分地震波作用下仍有部分楼层存在层侧移风险,这表明ηc=1.5仍不足以对柱端形成有效保护。
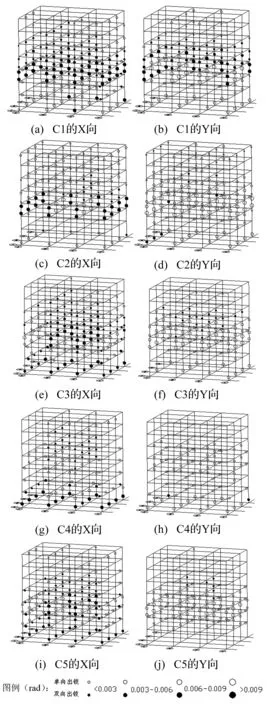
图3 USA00011波作用下7度0.15 g区框架的塑性铰分布Fig.3 Plastic hinges distributions of 7 earthquake intensity 0.15 g region frames under USA00011 wave
框架C4在USA00011波作用下基本避免了同一楼层全部柱端出现塑性铰(但USA02635波作用下的第5层仍有层侧移风险),且柱端转角明显减小,表明C4采用的∑Mc=1.8∑Mb有较明显的改善效果,但其柱铰多、梁铰少,抗震性态仍不够理想。
框架C5基于∑Mbua进行“强柱弱梁”控制,C5的塑性铰分布规律较C4稍差,其柱端转角、柱铰数量均高于C4,且在USA00011波作用下第3层有同一楼层全部柱端出现塑性铰的现象,表明C5的塑性铰控制效果比∑Mc=1.8∑Mb稍差。
结合表5、图2和图3综合分析后发现,抗规2001及抗规2010规定的“强柱弱梁”措施均难以对7度区三级抗震框架形成较好的塑性铰控制效果。罕遇地震作用下7度0.15 g区框架部分楼层形成“层侧移柱铰机制”的风险较大;7度0.1 g区框架虽然塑性铰数量少,但绝大部分塑性铰在柱端形成,这表明抗规2001和抗规2010的“强柱弱梁”措施均未能使其柱端抗弯承载力相对于梁端承载力得到足够增强,一旦遭遇“超烈度”地震作用,其塑性铰分布将与0.15 g区框架类似。
研究结果表明[5],7度0.1 g区和0.15 g区三级抗震框架即使ηc取值较大(对高烈度区框架该ηc取值已经能实现较理想的塑性铰控制效果),其柱端正截面承载力的增强幅度仍不明显。这主要有两方面原因,一是低烈度区框架由于地震作用小,中间节点左、右梁端Mb均为负弯矩的情况较为普遍,故造成其∑Mb比高烈度区明显更小;二是低烈度区梁端配筋与高烈度区相比小很多,同时不同烈度区的楼板钢筋基本没有差别(楼板钢筋由竖向荷载控制),故造成现浇板钢筋对低烈度区框架的梁端负弯矩实际承载力的增强幅度明显更大。
本文的计算结果进一步验证了文献[5]的上述分析结论。7度区框架的ηc提高至1.5左右时,其塑性铰控制效果仍难以得到明显改善,分析后发现,此时仍有部分柱的纵筋由ρmin控制,这表明对这部分柱端而言,ηc=1.5对柱纵筋的增强仍然未全面超过ρmin的影响;即使ηc取1.8,其塑性铰控制效果仍有不足,其原因在于7度区框架∑Mb小,相同的ηc对低烈度区柱配筋的增加幅度较高烈度区框架明显更低。
基于文献[5]的结论及上述计算结果本文认为,若仍保持现行抗震规范[1]的ηc取值格局,即7度区三级抗震框架的ηc较高烈度区框架的取值更低的情况下,改善7度区框架“强柱弱梁”措施的塑性铰控制效果的措施有:在计算∑Mb时增加“若节点左、右梁端均为负弯矩,绝对值较小的弯矩取零”的规定,并适当增加ηc的取值;此外,增设部分抗震墙预计可使前述不利局面得到明显改善。
4 “超烈度”下的分析结果和评价
我国在汶川地震中记录到了大量地面运动记录,其中主震记录最大的PGA为957.7 gal,断层附近21个台站记录中,PGA超过400.0 gal的加速度记录为16条[16]。汶川地震后,抗规2010将都江堰、汶川、北川、茂县等提高为8度0.2 g区,将绵竹、什邡、江油等提高为7度0.15 g区。这些事实均表明,结构遭遇超过设防烈度罕遇地震作用(“超大震”或“超烈度”)的可能性是客观存在的,避免“超烈度”下结构倒塌是抗震设计应考虑和重视的问题。
本文以7度0.1 g区框架B1和7度0.15 g区框架C1为例,分析“超烈度”对汶川地震中的7度区三级抗震框架结构普遍出现柱铰震害现象的影响。
框架B1输入在四川省江油市重华镇记录到的chnua370092波,其相关波为chnua370091,PGA分别为296.26 cm/s2和281.23 cm/s2;框架C1输入在四川省茂县南新镇记录到的chnua370181波,其相关波为chnua370182,PGA分别为420.52 cm/s2和349.34 cm/s2。可见,框架B1(大震PGA为220 cm/s2)、C1(大震PGA为310 cm/s2)均按2008年汶川地震前的抗规2001进行设计,输入的地震波则体现了“超烈度”影响(PGA较罕遇地震增大约40%~50%)。
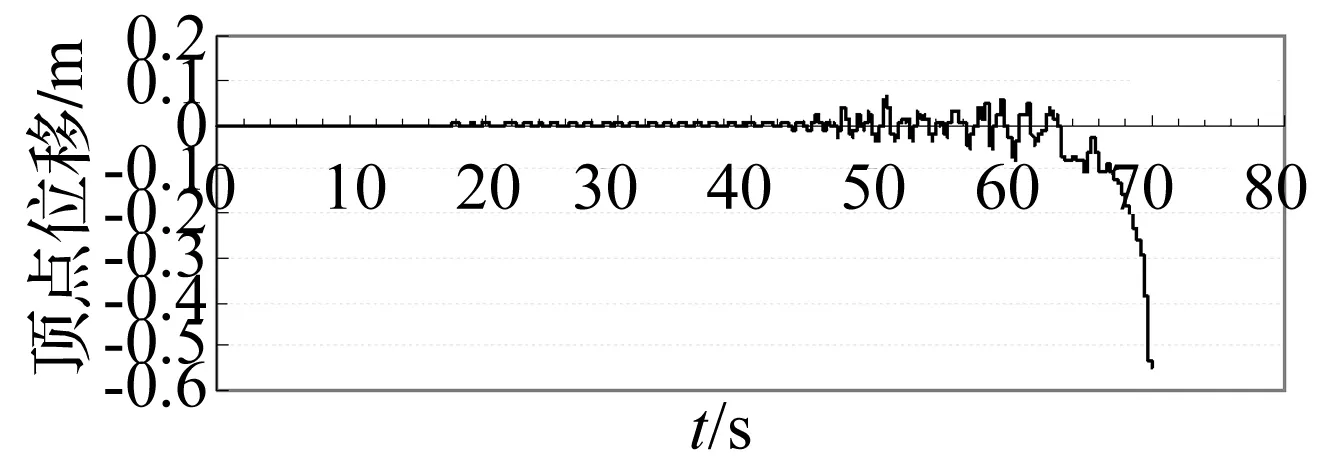
图4 超烈度下框架B1在X轴方向的顶点位移时程Fig.4 Top displacement time-history of frame B1 at X-axis under super intensity earthquake
表6给出的“超烈度”下框架最大顶点位移、X轴方向最大层间位移角表明,框架C1与表3给出的罕遇地震下的反应相近;框架B1的非线性反应较表3的结果显著增大。结合框架B1的顶点位移时程(见图4)可发现,在chnua370092波作用下,框架B1在约65 s后位移偏向一侧,并急剧加大,造成该现象的原因是,框架B1的最大层间位移位于底层(见表6),结构的塑性铰变形在底层集中,底层进入“层侧移”后在65~70 s导致整体结构处于失效状态。因此,表6仅给出了框架B1在70 s时的反应状态(后同)。

表6 超烈度下的最大顶点位移和最大层间位移角
表7的计算结果表明,框架B1在“超烈度”地震作用下由于非线性反应过大,其柱端混凝土纤维、钢筋纤维的最大应变以及柱端最大转角延性均远远超过材料的极限变形能力,说明部分位置的框架柱已经破坏。在这种情况下,其梁端出铰率仍仅为2.1%(梁端的最大纤维应变、最大转角延性需求也很小),表明框架B1是以柱端塑性铰耗能的方式抵抗“超烈度”的地震输入。框架C1在“超烈度”下也是通过柱端塑性铰耗散地震能量,其梁端出铰率仅1.8%,梁端的纤维应变、转角延性均很小;但与B1不同,虽然C1的柱端最大转角延性需求略偏大,但尚未导致结构完全失效(其钢筋最大拉应变、约束混凝土最大压应变均未超过1.0%)。
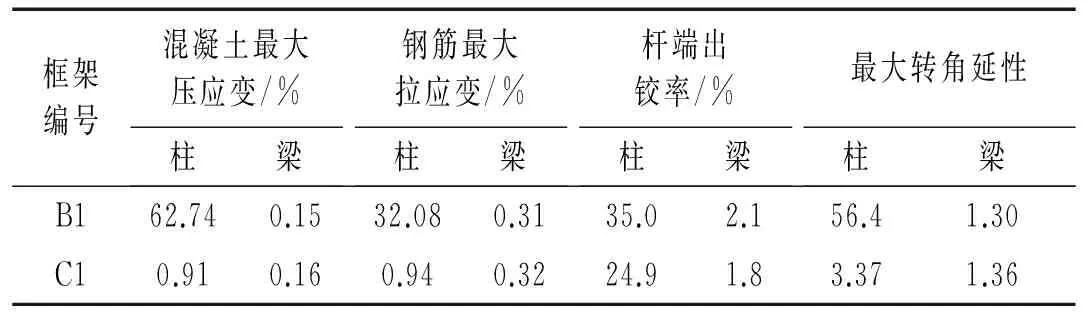
表7 超烈度下的纤维最大应变、杆端出铰率及最大转角延性
图5的塑性铰分布表明,框架B1和C1在超烈度地震下梁铰皆很少,且均有同一楼层全部柱端出现塑性铰的现象(B1在1、2层;C1在1、5、6层)。框架B1由于底层的层间位移很大,已在底层形成了“层侧移柱铰机制”(见表6),在图5(a)、5(b)中底层的柱端塑性铰转角大、双向出铰的柱端多也体现了这一特征。框架C1的柱端塑性铰转角相对更小,只要柱端能够提供足够的塑性变形能力(这取决于柱端箍筋的约束是否足够)和承载能力,即使框架存在同一楼层全部柱端出现塑性铰的现象,但其并不必然导致框架倒塌,当然结构的损伤非常严重。
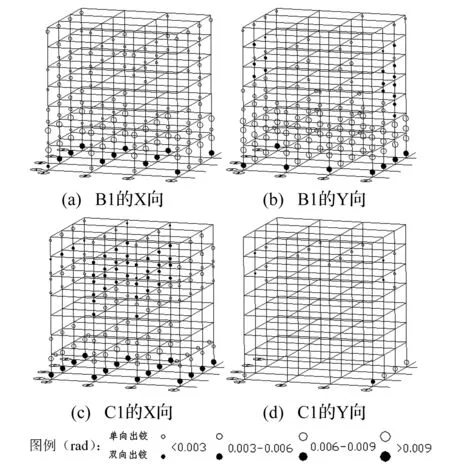
图5 超烈度下框架B1和C1的塑性铰分布Fig.5 Plastic hinges distributions of frame B1and C1 under super intensity earthquake
表7和图5表明,框架B1、C1在“超烈度”下均是通过柱铰耗能,这与汶川地震中7度区三级抗震框架结构普遍出现柱端塑性铰的震害现象是一致的。本文的分析结果表明,汶川地震中框架很少形成梁铰的震害现象除受现浇板、填充墙影响外,还与以下两个因素密切相关:第一,7度区三级抗震框架结构∑Mb小、现浇楼板的影响幅度更大、ηc取1.1无法对柱端形成有效增强,在地震动PGA不大时,梁端抗弯承载力比柱端更强的隐患尚不至于导致结构严重破坏;第二,结构遭遇了“超烈度”地震作用的影响,使得梁端抗弯承载力比柱端更强的后果以框架形成“层侧移柱铰机制”、甚至倒塌的震害现象表现出来。其中,超烈度对7度0.1 g区框架的不利影响更大,这与7度0.15 g区框架∑Mb相对更大、现浇楼板的影响幅度相对更小、更少柱纵筋由ρmin控制有关。
事实上,7度0.1 g区、0.15 g区三级框架在罕遇地震作用下塑性铰数量少,但均以柱铰为主的主要原因是:7度区三级框架的梁端负弯矩实际承载力因现浇板钢筋而较Mb(梁端截面抗震组合弯矩设计值)增大了约30%[5]、梁端正弯矩的实际承载力因为下部纵筋“超配”而较Mb增大了50%以上[5],框架柱的承载力也因其纵筋主要由最小配筋率ρmin控制而有所提高。因此,框架的实际承载力(由梁、柱的实际配筋决定)相对于小震水准的地震作用而言“超强”幅度较大,这相当于提高了结构整体的屈服水准,即减小了“地震力降低系数”R或“结构性能系数”q的取值,从而使得框架在罕遇地震作用下纵筋屈服时刻推迟、塑性铰数量减少,从表面上看结构的抗震性态控制效果尚可接受(特别是7度0.1 g区框架)。但其最大隐患是抗规2001[2]和抗规2010[1]的“强柱弱梁”措施均远不能真正使柱端抗弯承载力相对于梁端实际承载力得到足够增强,一旦遭遇“超烈度”地震作用(明显超过设防烈度罕遇地震的PGA),梁端实际抗弯承载力比柱端更强的隐患将发挥作用,并造成柱端严重损伤。这正是汶川地震中北川、汶川、都江堰、茂县等地遭遇”超烈度”地震作用后,框架结构形成了柱端普遍出现塑性铰、甚至因形成“柱铰机制”而倒塌的震害现象的主要原因之一。
5 结 论
通过分析7度0.1 g区和0.15 g区三级抗震框架结构在双向水平地震作用下的非线性反应,得到以下主要结论。
(1) 抗规2001给出的7度0.1 g区和0.15 g区三级抗震的柱端弯矩增强措施(ηc=1.1)取值明显偏低,罕遇地震作用下框架的塑性铰数量不多,但绝大部分塑性铰在柱端形成。按现行抗规2010提高“强柱弱梁”措施后(ηc=1.3)后,框架的塑性铰分布特征改善幅度很小。
(2) 罕遇地震下7度0.1 g区、0.15 g区三级框架塑性铰数量少,其主要原因是由梁、柱实际配筋决定的框架实际承载力相对于小震水准的地震作用而言“超强”幅度较大,提高了结构整体的屈服水准。
(3) 在超过罕遇地震PGA约40%~50%的“超烈度”地震波作用下,按抗规2001设计的7度区空间框架的地震反应与汶川地震中普遍出现柱端塑性铰的震害现象一致。
(4) 汶川地震中很少形成梁铰的震害现象除受填充墙等影响外,还与以下两个因素密切相关:① 7度区框架∑Mb小、现浇板的影响幅度更大、ηc取1.1无法对柱端形成有效增强;② 遭遇了“超烈度”地震作用的影响后,梁端抗弯承载力比柱端更强的隐患发挥作用。
(5) 建议在现行抗规2010的基础上进一步增大7度区三级抗震的ηc(如1.5左右),同时计算∑Mb时采用“当节点左、右梁端均为负弯矩时,绝对值较小的弯矩取零”的规定。
[1] (GB50011-2010),中华人民共和国住房和城乡建设部. 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.
[2] (GB50011-2001),中华人民共和国住房和城乡建设部. 建筑抗震设计规范[S]. 北京:中国建筑工业出版社, 2001.
[3] 杨红,韦锋,白绍良,等. 柱增强系数取值对钢筋混凝土抗震框架塑性铰机构的控制效果 [J]. 工程力学, 2005, 22(2): 155-161.
YANG Hong, WEI Feng, BAI Shao-liang, et al. Effect of moment amplification factors of columns on controlling plastic hinge mechanism of RC frames [J]. Engineering Mechanics, 2005, 22(2):155-161.
[4] 杨红,张和平,骆文进,等. 双向地震下RC框架柱端弯矩增强措施的合理取值[J]. 四川大学学报:工程科学版, 2012, 44(1): 19-27.
YANG Hong, ZHANG He-ping, LUO Wen-jin, et al. Rational value of moment amplification measures at column ends in RC frames under bi-directional horizontal seismic acion [J]. Journal of Sichuan University:Engineering Science Edition, 2012, 44(1): 19-27.
[5] 杨红,孙永炜,张睿,等. 基于梁铰机制的柱端弯矩增强措施研究[J]. 土木工程学报, 2014, 47(4): 64-74.
YANG Hong, SHUN Yong-wei, ZHANG Rui, et al. A study on the moment amplification measures of column ends based on the beam sidesway mechanism [J]. China Civil Engineering Journal, 2014, 47(4): 64-74.
[6] 王亚勇.汶川地震建筑震害启示-抗震概念设计[J]. 建筑结构学报, 2008, 29(4):20-25.
WANG Ya-yong.Lessons learnt from building damages in the Wenchuan earthquake—seismic concept design of building[J]. Journal of Building Structure, 2008, 29(4): 20-25.
[7] 叶列平,曲哲,马千里,等. 从汶川地震中框架结构震害谈“强柱弱梁”屈服机制的实现[J]. 建筑结构, 2008, 38(11):52-59.
YE Lie-ping, QU Zhe, MA Qian-li, et al. Study on ensuring the strong column-weak beam mechanism for RC frames based on the damage analysis in the Wenchuan earthquak[J]. Building Structure, 2008, 38(11):52-59.
[8] 杨红,朱振华,白绍良. 双向地震作用下我国“强柱弱梁”措施的有效性评估 [J]. 土木工程学报,2011,44(1):58-64.
YANG Hong, ZHU Zhen-hua, BAI Shao-liang. An evaluation on the effectiveness of Chinese strong column weak beam measure under bi-directional horizontal seismic excitation[J].China Civil Engineering Journal,2011,44(1):58-64.
[9] (GB50010-2010),中华人民共和国住房和城乡建设部. 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.
[10] Mazzoni S, McKenna F, Scott M H, et al. Open system for earthquake engineering simulation users command-language manual[M/OL]. University of California, Berkeley, 2014. http://opensees.berkeley.edu/wiki/index.php/Command_Manual.
[11] Kent D C and Park R. Flexural members with confined concrete[J]. Journal of Structural Engineering, ASCE, 1971,97(ST7):1969-1990.
[12] Scott B D, Park R and Priestley M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J]. ACI Journal, 1982,79(1):13-27.
[13] 杨红,王建辉,白绍良. 双向地震作用对柱端弯矩增强系数的影响分析 [J]. 土木工程学报, 2008, 41(9):40-47.
YANG Hong, WANG Jian-hui, BAI Shao-liang. The effect of bi-directional horizontal seismic excitation on the moment amplification factor of columns [J]. China Civil Engineering Journal, 2008, 41(9):40-47.
[14] Filippou F C, Popov E P,Bertero V V. Nonlinear static and dynamic analysis of concrete subassemblages[R]. Berkeley: University of California at, EERC Report No. 92/08, 1992.
[15] 杨红,任小军,徐海英. 双向水平地震下时程分析法中输入波的选择 [J]. 华南理工大学学报:自然科学版, 2010, 38(11):40-46.
YANG Hong, REN Xiao-jun, XU Hai-ying. Selection of input wave in time-history analysis under bi-direction horizontal seismic action [J]. Journal of South China University of Technology:Natural Science Edition, 2010, 38(11):40-46.
[16] 于海英,王栋,杨永强,等. 汶川8.0级地震强震动特征初步分析 [J]. 震灾防御技术, 2008, 3(4):321-336.
YU Hai-ying, WANG Dong, YANG Yong-qiang,et al. The preliminary analysis of strong ground motion characteristics from the Ms8.0 Wenchuan Earthquake [J]. Technology for Earthquake Disaster Prevention, 2008, 3(4):321-336.
“Strong column weak beam” measures for RC frame structures in 7 seismic intensity area under bi-directional horizontal seismic excitations
YANG Hong1,2, REN Xiao-jun3, BAI Shao-liang1,2
(1. School of Civil Engineering, Chongqing University, Ministry of Education, Chongqing 400045, China;2. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Chongqing University, Ministry of Education, Chongqing 400045, China;3. Chongqing Research & Design Institute of Sino-Coal International Engineering Group, Chongqing 400016, China)
Based on damage characteristics of Wenchuan earthquake that plastic hinges of reinforced concrete (RC) frame structures appeared prevalently at column ends, the influences of “strong column weak beam” measures and super intensity earthquake on aseismic performance of structures were analyzed. Regular spatial frames for 7 earthquake intensity 0.1 g region and 0.15 g region were designed according to the specifications of the 3rd class aseismic rules in Chinese code, respectively. By increasing “strong column and weak beam” measures gradually, five examples for each kind for 7 earthquake intensity regions’ frames were obtained. Based on the OpenSees framework, nonlinear responses of every frame under bi-directional horizontal earthquake excitations were calculated. The results showed that when the “strong column and weak beam” measures of code GB50011-2001 are adopted, for 7 earthquake intensity 0.1 g region’s frame, the number of plastic hinges is less, almost all plastic hinges appear at column ends under rare earthquake; while for 0.15 g region’s frame, the number of plastic hinges is larger, plastic hinges rarely appear at beam ends; when the value of the moment amplification factor of column end of the 3rd class aseismic rule is improved according to the aseismic code GB50011-2010, almost no improvement of plastic hinges distribution can be found; the characteristics of plastic hinges distribution for 7 earthquake intensity regions’ frames designed with the “strong column and weak beam” measures of code GB50011-2001 under super intensity earthquake are plastic hinges appearing prevalently at column ends, they are consistent with damage characteristics of Wenchuan earthquake; for the frames of 7 earthquake intensity regions, the dangerous plastic hinges distribution characteristics are due to comprehensive effects of smaller combination moment of beam ends, bigger influence of reinforcement of site casting slab, too weak “strong column and weak beam” measures and super intensity earthquake.
reinforced concrete (RC); 3D frame; bi-directional horizontal seismic excitation; strong column weak beam; nonlinear analysis
10.13465/j.cnki.jvs.2016.13.008
国家自然科学基金(51178487)
2015-03-24修改稿收到日期:2015-07-09
杨红 男,博士,教授,博士生导师,1969年生
TU311.3
A
