层合板结构声辐射模态传感器分析与测量

吴锦武， 原海朋， 毛崎波

(南昌航空大学 飞行器工程学院，南昌　330063)

层合板结构声辐射模态传感器分析与测量

吴锦武， 原海朋， 毛崎波

(南昌航空大学 飞行器工程学院，南昌330063)

利用压电高分子材料聚偏氟乙烯(Polyvinylidene fluoride，PVDF)设计一种阵列式传感器来测量复合材料层合板结构的声辐射模态幅值。以声辐射模态传感器设计理论作为基础，进一步分析了声辐射模态传感器的测量精度影响因素，即粘贴位置和粘贴方向等。利用了声辐射模态传感器对层合板结构的固有频率、声辐射模态幅值以及声功率的进行测试分析。并对实验数据与理论仿真结果进行了分析。

层合板；声辐射模态；压电传感器；测试分析

由于复合材料具有高强度，高模量，低密度及很强的可设计性，复合材料层合板已广泛应用于航空航天等领域。当复合材料层合板受到外界激励会产生辐射噪声。对于航空复合层合板结构而言，大多数复合材料层合板结构振动一般处于中低频振动。而在中低频率时，控制振动结构的前几阶声辐射模态幅值即可有效降低振动结构总声功率[1-2]。

近几年来，利用高分子压电薄膜聚偏氟乙烯(Polyvinylidene fluoride，PVDF)作为传感器测量结构声辐射模态幅值或体积速度的应用越来越广泛[3-6]。其中大多数研究主要采用分布式PVDF传感器[3-5]与阵列式PVDF传感器[6-9]两种，阵列式PVDF传感器测量声辐射模态幅值克服了分布式传感器设计形状复杂，加工困难等缺点，更适用于工程应用。此前，研究人员对梁结构及单层板结构的声辐射模态幅值和体积速度及体积位移信息进行了相应的理论设计及实验研究[8-9]。

针对复合材料层合板结构声辐射模态幅值的测量，吴锦武等[1]从理论上分析了利用分层理论结合有限元模型，设计一种阵列式声辐射模态传感器的可行性。由于复合材料层合板相对普通单层板结构而言，材料为各向异性，结构参数多，而且复合材料层合板结构存在纤维方向布置问题，因此本文以文献[1]中的声辐射模态传感器设计理论为基础，进一步研究影响声辐射模态传感器测试精度的因素，以及着重从实验角度，对层合板结构声辐射模态传感器的进行测试设计。

1　声辐射模态传感器设计

由文献[1]可知，采用阵列式PVDF薄膜可设计振动板结构的声辐射模态传感器。设计思路如下：假设有J块形状相同的矩形PVDF薄膜均匀粘贴在层合板结构表面，如图1所示。

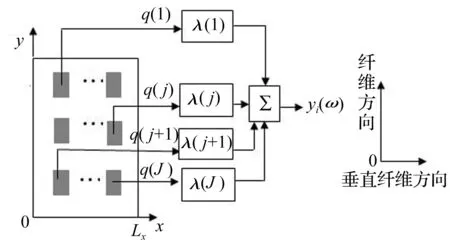
图1　层合板表面PVDF传感器阵列图Fig.1 PVDF array sensors of laminate composite plate

(1)

式中：M为最大截断模态数；Bi(ω)振动板表面的法向速度按振动模态展开的系数；Bi(ω)和H矩阵元素见文献[1]。

由文献[1]可知：对于第k阶声辐射模态幅值yk(ω)：

(2)

式中：Ai元素见文献[1]。

通过对每块PVDF薄膜设计不同的加权系数λ(j)可满足：

(3)

比较式(1)和式(2)，可得矩阵形式[1]：

H Λ=A⟹Λ=H+A

(4)

由式(3)～式(4)可知，通过调整每块PVDF薄膜加权系数λ(j)，可得到所需的声辐射模态幅值，即称PVDF阵列式传感器为声辐射模态传感器。文献[1]利用首先通过分层理论结合有限元模型获得离散振动模态，通过曲线拟合方法可获得振动模态表达式。

2　数值计算与分析

考虑一个16层0度铺设的T300层合板，其结构参数如表1所示。

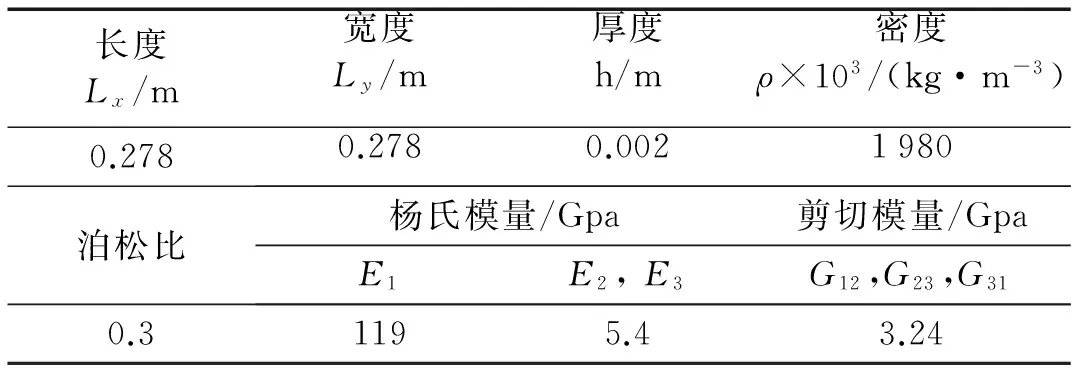
表1　T300层合板的结构参数

由分层理论结合有限元方法[1],可获得固支边界条件下层合板前几阶振动模态的固有频率，如表2所示。其中m,n分别为板沿x和y方向的振动模态阶数。

在层合板上均匀粘贴A×B块PVDF压电薄膜，其中每块PVDF压电薄膜的长度为0.03 m，宽度为0.012 m，厚度为28 μm，压电常数e31=1.05×10-2C/m2，e32=3.5×10-4C/m2。本文中PVDF压电薄膜均采用该参数。

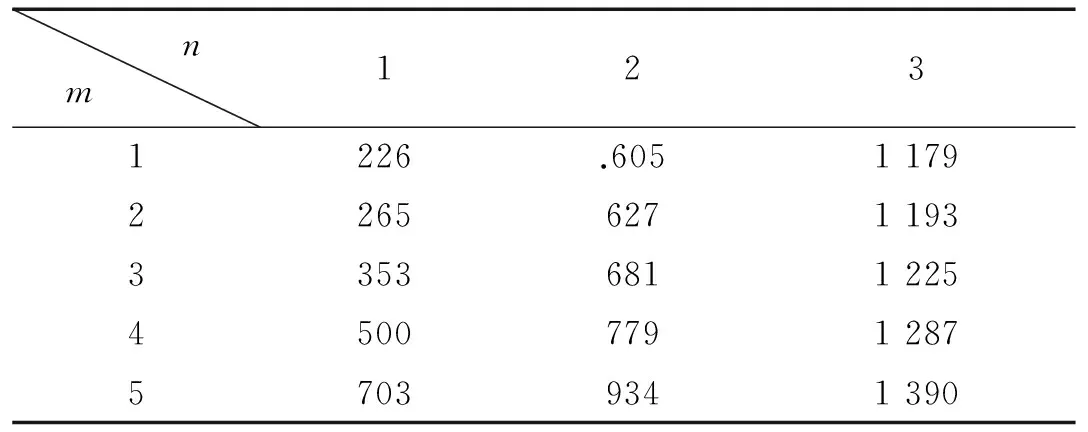
表2　固支层合板的固有频率(Hz)

设PVDF阵列式传感器按照5×5共25片PVDF薄膜均匀粘贴在层合板表面，矩形PVDF薄膜的长度方向平行于层合板纤维方向。在层合板中点位置施加单位简谐激励力。根据式(4)得到各片PVDF薄膜的加权系数，根据式(2)可获得层合板的第一阶声辐射模态幅值。图2(a)为PVDF薄膜长度沿层合板纤维方向均匀粘贴时得到的加权系数，图2(b)理论层合板第一阶声辐射模态幅值与PVDF传感器模拟值的对比。

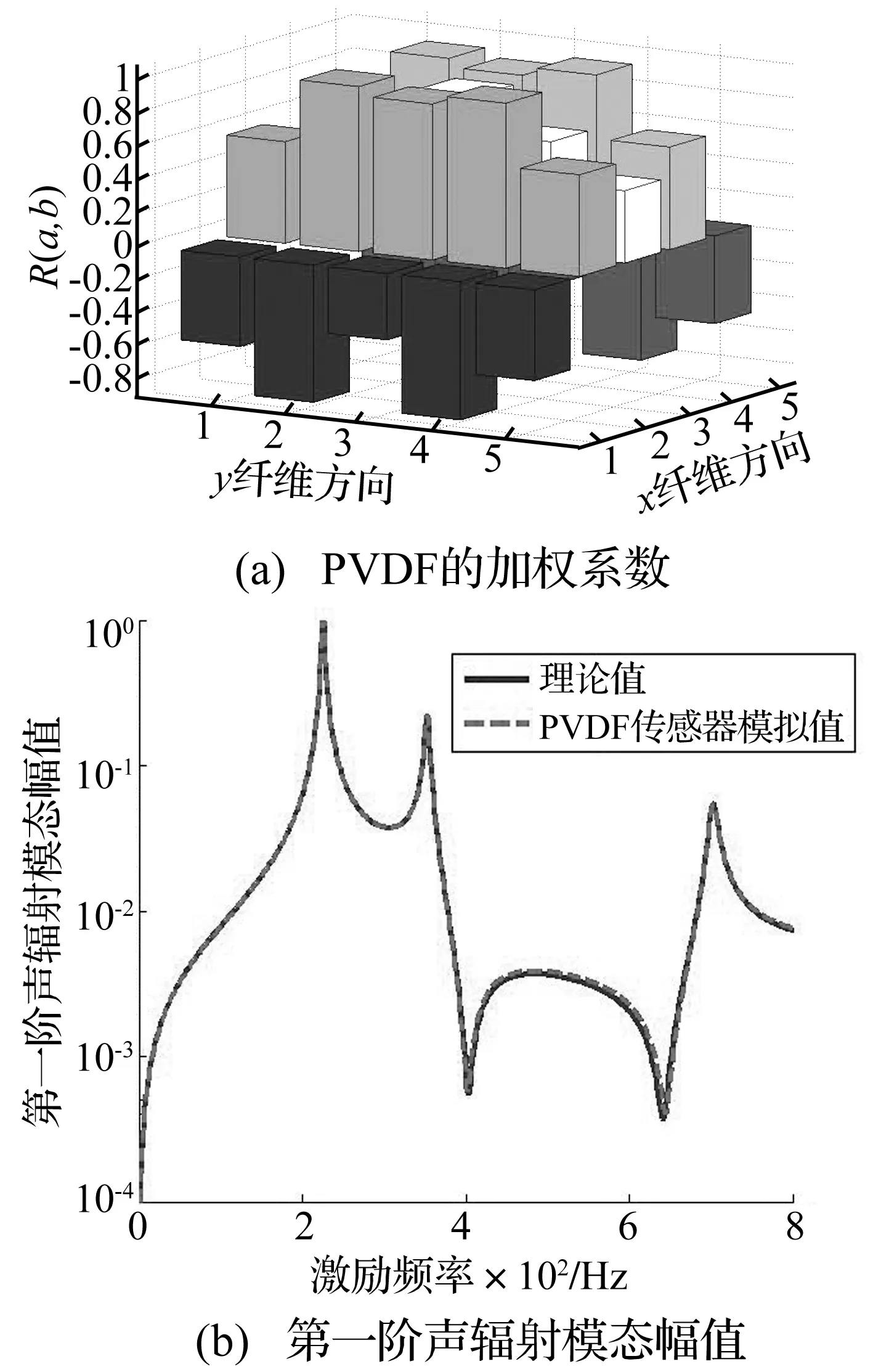
图2　PVDF沿纤维方向粘贴时加权系数与声辐射模态幅值Fig.2 The weight coefficient and the first radiation mode amplitude when PVDF sensors are pasted along the fiber direction

由图2(b)可知的PVDF输出结果与层合板理论声辐射模态幅值曲线基本吻合，说明阵列式PVDF压电薄膜能够测量层合板声辐射模态幅值。另外由文献[8]可知：PVDF阵列式传感器中PVDF薄膜的数目越多，随着频率越高，测量结果越准确。

2.1压电薄膜粘贴方向的影响

由于复合材料层合板结构一般存在纤维材料，同时纤维铺设角度存在多样性。纤维铺设角度影响层合板结构的刚度。图2(b)为PVDF薄膜长度方向平行与纤维方向时得到的第一阶声辐射模态幅值。当PVDF薄膜数目、激励力位置和幅值和图2都一致时，而PVDF长度方向垂直于纤维方向粘贴，得到的第一阶声辐射模态幅值如图3所示。

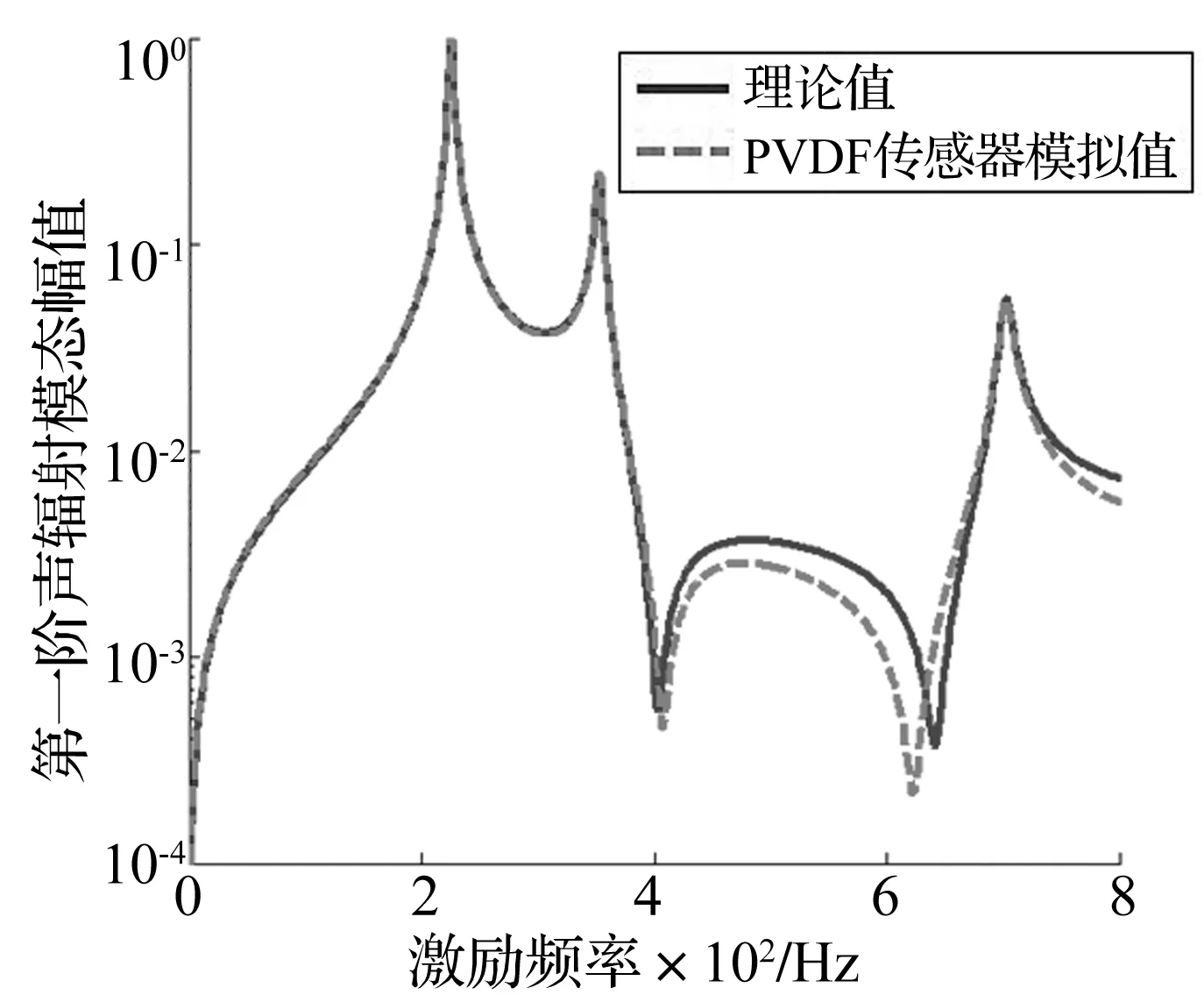
图3　垂直纤维方向粘贴的测量结果Fig.3 The first radiation mode amplitude of the plate when PVDF sensors are perpendicular to the fiber direction

对比图2(b)和图3可知：在采用相同PVDF阵列式传感器测量层合板第一阶声辐射模态幅值，矩形PVDF薄膜长度方向沿层合板纤维方向粘贴得到的结果要优于垂直纤维方向得到的结果。这主要是因为层合板纤维方向上的刚度较垂直纤维方向大，在相同激励力作用下横向形变小，对PVDF测量层合板纵向振动的振动信息影响更小，测量结果更准确。因此，实际测量层合板声辐射模态幅值时，应尽量使矩形PVDF压电薄膜长度方向沿层合板纤维方向粘贴。

2.2压电薄膜粘贴位置偏差的影响

PVDF压电薄膜的粘贴位置偏差对测量结果有一定的影响。采用图2相同的PVDF薄膜数目、激励力位置和幅值，图4为第(3,3)片PVDF压电薄膜沿纤维方向偏移3 mm时，PVDF阵列传感器测量到的第一阶声辐射模态幅值与理论值的对比情况。

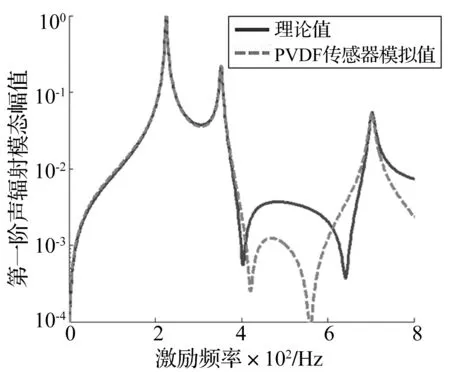
图4　PVDF沿纤维方向偏移3mm获得的测量结果Fig.4 The first radiation mode amplitude of the plate when there is 3mm offset error between PVDF sensors and the fiber direction

由图4可看出，PVDF薄膜布置位置准确性对PVDF阵列式传感器测量结果有明显的影响。实际中既要使PVDF薄膜长度方向沿层合板结构纤维方向，同时要保证粘贴位置的准确。

2.3激励力位置的影响

根据式(4)可看出，加权系数与激励力位置/大小无关。当激励力为单位激励时，采用同一组加权系数获得不同激励位置下的第一阶声辐射模态幅值并与理论值对比。图5(a)为中点激励PVDF测量值；图5(b)为相同加权系数条件下，非中点激励获得的第一阶声辐射模态幅值与理论值的对比。

由图5(b)可知，PVDF测量值与理论值两条曲线吻合，验证了式(4)的结果：即加权系数与激励力的位置无关，亦可应用于测量任意激励位置下的声辐射模态幅值。

图5　第一阶声辐射模态幅值Fig.5 The first radiation mode amplitude of the laminate composite plate

3　实验分析

复合材料层合板结构声辐射模态测量的实验装置简图见图6。复合材料层合板结构参数见表1。在实验中，T300层合板被固定在实验台架上，在板中点处设置单位激励力，激励最大频率为800 Hz。所有实验仪器都进行标定, 测量到的信号都转换成工程单位。

在实验中，由于实验结构与数值分析时复合材料结构参数并不一致，同时考虑整个实验台架和边界条件(在数值分析时层合板结构是四边完全固定边界条件，而在实验中层合板结构四周用16个用螺栓固定来模拟固定边界条件)。考虑实际板结构参数以及边界条件，难以利用分析计算方法得到理论第一阶声辐射模态。在此采用振动测量方法得到振速分布，进而获得层合板的第一阶声辐射模态幅值：在其表面均匀测量36个点振动速度响应，通过式(2)计算可获得层合板结构第一阶声辐射模态幅值，作为实际第一阶声辐射模态幅值。采用图6所示的PVDF阵列式传感器测量第一阶声辐射模态幅值。实验中加速度传感器(型号：BZ1102)和8通道信号采集处理分析仪(型号：INV360U)均为北京东方振动和噪声技术研究所生产。

3.1固有频率测量

由于PVDF压电高分子材料非常薄，质量轻，作为传感器使用，相比传统加速度传感器而言，对振动结构本身影响非常小。

PVDF压电薄膜沿层合板结构纤维方向粘贴，采用5×6共30片PVDF薄膜作为阵列式传感器均匀粘贴在层合板的表面，如图6所示。实验中用B&K4808力锤敲击板的中点，测量得到输入力与各个PVDF之间的传递函数，从传递函数可获得层合板的各阶固有频率。层合板固有频率与理论固有频率对比见表3。

图6　PVDF传感器实验装置Fig.6 The setup of the PVDF array sensors

从表3可知，PVDF阵列式传感器测量到的层合板固有频率在低频时，结果基本吻合，随着频率增加，两者之间有一定误差。这是因为随着频率增加，实际层合板结构与理论模拟存在一定差异，如边界条件和层合板结构参数不稳定性等。

3.2声辐射模态幅值测量

图7为计算得到的PVDF加权系数直方图。将测量到的传递函数乘以相应的加权系数后得到层合板声辐射模态幅值。

图8为通过加速度计测量得到的声辐射模态幅值与通过PVDF阵列得到的实验结果比较。从图8可知：PVDF阵列式传感器测量值与加速度计测量结果趋势基本一致，吻合程度较好。在400～600 Hz之间有些差异。这是因为PVDF薄膜作为传感器，其对其他振动信号如板内横向振动、内部结构损伤等较敏感，会引起结果的偏差。这同时也可说明PVDF薄膜作为传感器具有的另一特点。

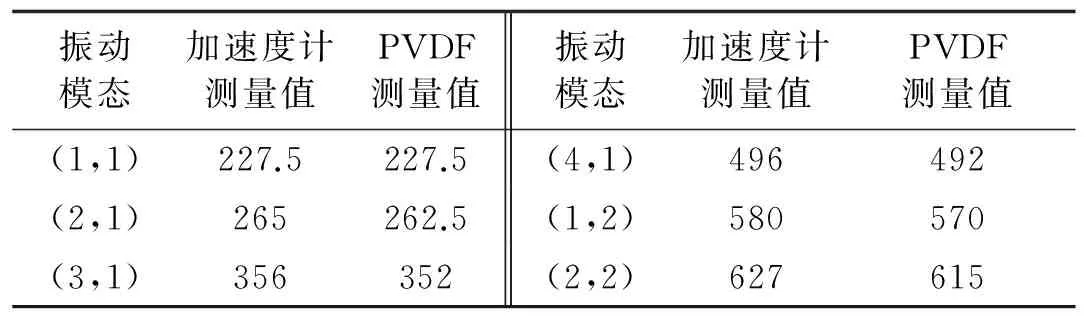
表3　固支层合板固有频率的测量值(Hz)

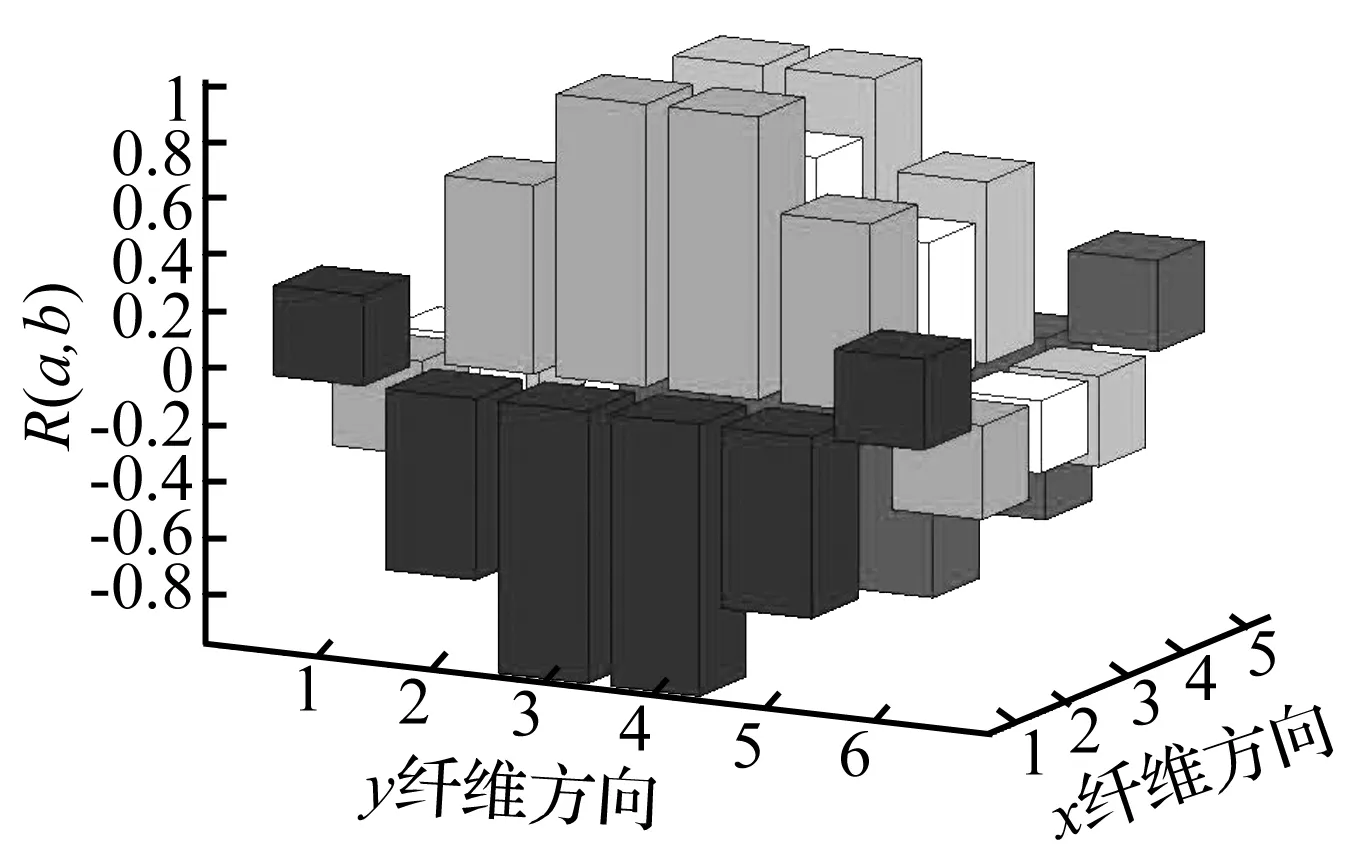
图7　5×6分布PVDF传感器加权系数Fig.7 The weight coefficients of 5×6 PVDF array sensors

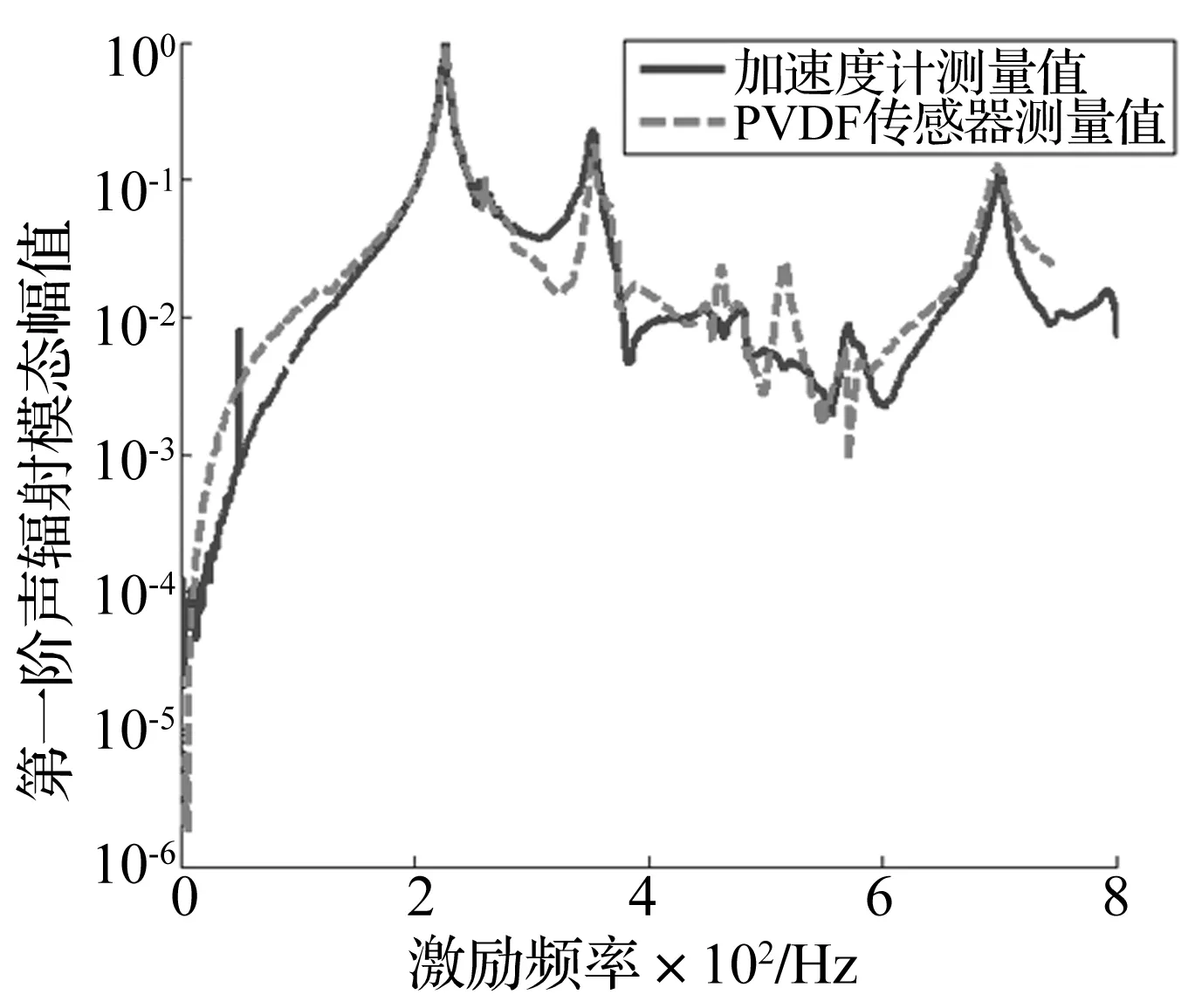
图8　层合板声辐射模态幅值(中点激励)Fig.8 The first radiation mode amplitude of the laminate composite plate (midpoint force)

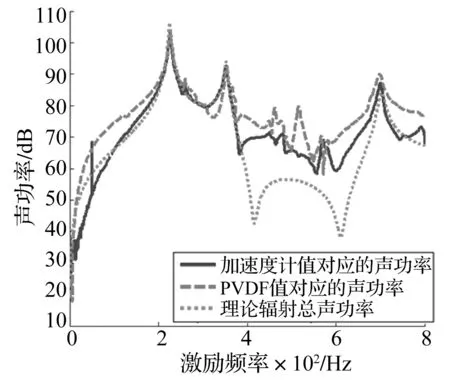
图9　层合板结构的声功率Fig.9 The radiation acoustic power of the laminate composite plate (midpoint force)

已知第一阶声辐射模态信息，利用文献[1]中式(3)可计算得到辐射声功率。图9为由PVDF测量得到第一阶声辐射模态幅值、加速度计测量得到声辐射模态幅值计算得到的声功率与理论辐射总声功率比较图。由图9可知：三条曲线对应的固有频率基本一致，曲线变化趋势基本相同，但在第(3,1)阶固有频率：352 Hz至第(5,1)阶固有频率：702 Hz之间，PVDF传感器测量值对应得到的声功率，加速度测量值对应的声功率与理论声功率之间有差异。当中点激励时，对理论声功率起主要贡献的只是(奇，奇)阶振动模态；但从实际测量结果可知：352～702Hz存在其他非(奇，奇)阶振动模态，这与实际结构边界条件以及实验台有关。

4　结　论

(1) PVDF声辐射模态传感器测量结果与每片PVDF薄膜粘贴位置密切相关。

(2) 为了测量结果更准确，必须使声辐射模态传感器长度方向沿层合板纤维方向布置。

(3) PVDF声辐射模态传感器应用范围广，即可测量层合板结构的声辐射模态幅值，又可有效测量层合板结构固有频率。而且由于PVDF薄膜作为传感器，相比加速度传感器，质量轻，厚度薄，对振动结构影响小，测量结果更准确。

[1] 吴锦武, 赵龙胜, 黄凌志.基于分层理论的层合板结构声辐射模态传感器设计[J].机械工程学报, 2014, 50(3):116-121.

WU Jin-wu, ZHAO Long-sheng, HUANG Ling-zhi.Design of acoustic radiation modes sensors of the laminated composite plates based on layerwisetheory [J].Chinese Journal of Mechanical Engineering, 2014, 50(3):116-121.

[2] Elliott S J, Johnson M E. Radiation modes and the active control of sound power [J].The Journal of the Acoustical Society of America, 1993, 94(4):2194-2204.

[3] 陈克安, 陈国跃, 李双, 等.分布式位移传感下的有源声学结构误差传感策略[J].声学学报, 2007, 32(1):42-48.

CHEN Ke-an, CHEN Guo-yue, LI Shuang, et al.Error sensing strategy for active acoustic structure based on distributed displacement sensors[J].Chinese Journal of Acoustics, 2007, 32(1):42-48.

[4] Gardonio P, Lee Y S, Elliot S J, et al. Analysis and measurement of a matched volume velocity sensor and uniform force actuator for active structural acoustic control [J].Journal of the Acoustical Society of America, 2001, 110(6):3025-3031.

[5] 杜敬涛, 靳国永, 杨铁军,等.基于分布式压电传感器的结构表面体积速度测量实验研究[J].振动工程学报, 2008, 21(3):235-240.

DU Jing-tao, JIN Guo-yong, YANG Tie-jun, et al. Experimental research on the volume velocity of vibration structure based on distributed piezoelectric sensor [J].Journal of Vibration Engineering, 2008, 21(3):235-240.

[6] Preumont A, François A, Dubru S. Piezoelectric array sensing for real-time, broadband sound radiation measurement[J].ASME Trans. J. Vibration and Acoustics, 1999, 121(4):446-452.

[7] Tanaka N, Snyder S D, Hansen C H. Distributed parameter modal filtering using smart sensors [J].Transactions of ASME Journal of vibration and acoustic, 1996, 118(4):630-640.

[8] 吴锦武, 张加林, 王云.通过阵列传感器获取固定板声辐射模态伴随系数[J].振动与冲击, 2008, 27(1):104-106.

WU Jin-wu, ZHANG Jia-lin,WANG Yun. Acquiring adjoint coefficients of acoustic radiation modes of a clamped-clamped plate using array sensors [J].Chinese Journal of Vibration and Shock, 2008, 27(1):104-106.

[9] Mao Qi-bo, Xu Bo-ling, Jiang Zhe, et al, A piezoelectric array for sensing radiation modes [J].Applied Acoustics, 2003, 64(7):669-680.

Analysis and test of acoustic radiation mode sensors of laminated composite plates

WU Jin-wu, YUAN Hai-peng, MAO Qi-bo

(School of Aircraft Engineering, Nanchang Aeronautical University, Nanchang 330063, China)

An array type sensor was designed with polyvinylidene fluoride and the sensor could be used to measure acoustic radiation modes’ amplitudes of a laminated composite plate. Using the design theory of acoustic radiation mode sensors published, the measurement accuracy factors of the sensor were analyzed, such as sensor pasted location and direction. Natural frequencies, the first order acoustic radiation mode’s amplitude and the acoustic radiation power of the laminated composite plate were measured with the sensor. The tests results and the numerical simulation results were analyzed.

laminated composite plates; radiation modes; piezoelectric sensors; test analysis

10.13465/j.cnki.jvs.2016.13.005

国家自然科学基金项目(51265038)

2015-03-19修改稿收到日期：2015-05-11

吴锦武 男，博士，教授，1976年9月生

TB332；TH113.1

A