双弯曲管式螺杆型压电作动器

华顺明， 孟玉明，2， 楼应侯， 李志强，2， 李加林，2

(1. 浙江大学 宁波理工学院，浙江　宁波　315100； 2. 太原科技大学 机械工程学院，太原　030024)

双弯曲管式螺杆型压电作动器

华顺明1， 孟玉明1，2， 楼应侯1， 李志强1，2， 李加林1，2

(1. 浙江大学 宁波理工学院，浙江宁波315100； 2. 太原科技大学 机械工程学院，太原030024)

提出一种基于压电金属复合梁双向弯曲振动的螺杆型作动器，其压电换能器中每一个压电片都工作在Kt模态。首先，以细直梁在空间的一阶弯曲振型为基础确定了作动器结构形式；其次，对定子材料、结构参数与固有频率及端面振幅的关系进行了有限元分析，其中特别讨论了材料的参数E/ρ对一阶固有频率的影响规律；然后，根据分析结果确定了作动器结构尺寸，并试制了样机；最后，测试了样机的主要输出特性。结果表明，作动器的最佳激振频率约为15.8 kHz，启停时间在20 ms左右；在300 V驱动电压下，作动器最大空载速度为1.146 mm/s，最大轴向力为2.5 N。

作动器；压电金属复合梁；弯曲振型；机械特性

目前，将压电材料的超声振动和精密螺旋传动相结合的作动器，多为贴片式结构。该类作动器结构简单、工作原理清晰，国内外均有学者对该类电机进行过研究。2005年美国Henderson的Squiggle电机问世[1-3]，该电机可以产生0.5 N的输出力以及2 mm/s的输出速度，位置分辨率可达20 nm；赵淳生[4]利用动力学分析方法推导了螺纹杆式超声电机定子驱动点的运动方程，阐述了该类电机的运行机理；清华大学物理系与博立码杰通讯有限公司合作，研制了一种面内弯曲行波的螺母型超声电机[5]，该电机的定子为短筒状，外表面做成类似螺母的多面体，内表面做出内螺纹与外螺纹镜头形成配合。

但是，贴片式作动器也存在以下问题[6]。首先，压电换能器工作在低机电耦合效率的d31模式，且陶瓷材料的低抗拉强度也限制了定子弹性体振幅的提高；其次，定子的金属基体与陶瓷片为黏结连接，胶层强度和疲劳等问题使得定子振幅必须控制在合理范围内，不能过大，极端环境下胶层特性改变也会影响作动器运行的稳定性；最后，该类作动器大都基于环形定子的轴向弯曲振动模态，定转子接触面局限于定子外沿很小的区域内，其他部位虽然也存在弹性势能及动能，但没有转化为输出能量，因此振动能量利用率低。夹心换能器式作动器则利用压电陶瓷的Kt模态，并通过机械预紧使得陶瓷始终工作在压应力状态，从而可以极大地提高激励强度。为此，本文利用压电陶瓷的Kt模态，用夹心式换能器代替贴片式换能器作为该类作动器的定子，结合精密螺旋传动，将定子与转子通过精密螺旋副相啮合，讨论一种双弯曲管式螺杆型压电作动器。

1　作动器结构及其工作原理

1.1作动器结构

作动器包括定子组件和转子组件两部分，如图1(a)所示。定子组件主要由定子主体、压套和PZT构成，其中压套与定子主体螺纹连接，并通过上下圆环垫片压紧PZT组，垫片可使PZT组受力均匀，防止因受力不均而出现碎片现象；转子组件由螺杆、驱动螺母和导套构成。为保证定子主体、驱动螺母和导套的同轴度，将三者以过盈配合装配后，在SPINNER PD/C-TMC精密车削中心上装夹，一次完成内外轮廓及螺纹的精加工。

压电陶瓷均沿厚度方向极化，布局和引线方式如图1(b)所示。以A相为例，每只PZT环对称切分为两个半片，二者极化方向相反，上下相邻半片的极化方向亦相反。B相与A相在空间正交。当A相施加Ucosω1t时(ω1约为一阶固有弯振频率)，定子将产生左右弯曲共振；同理，当B相施加Ucos(ω1t+φ)时，定子产生前后弯曲共振。A、B两相同时工作时，定子会产生空间的一阶弯曲共振运动，并在其端面产生一个波长的行波。继而通过螺母和螺杆之间的接触摩擦力，实现螺杆的旋转-直线复合运动。

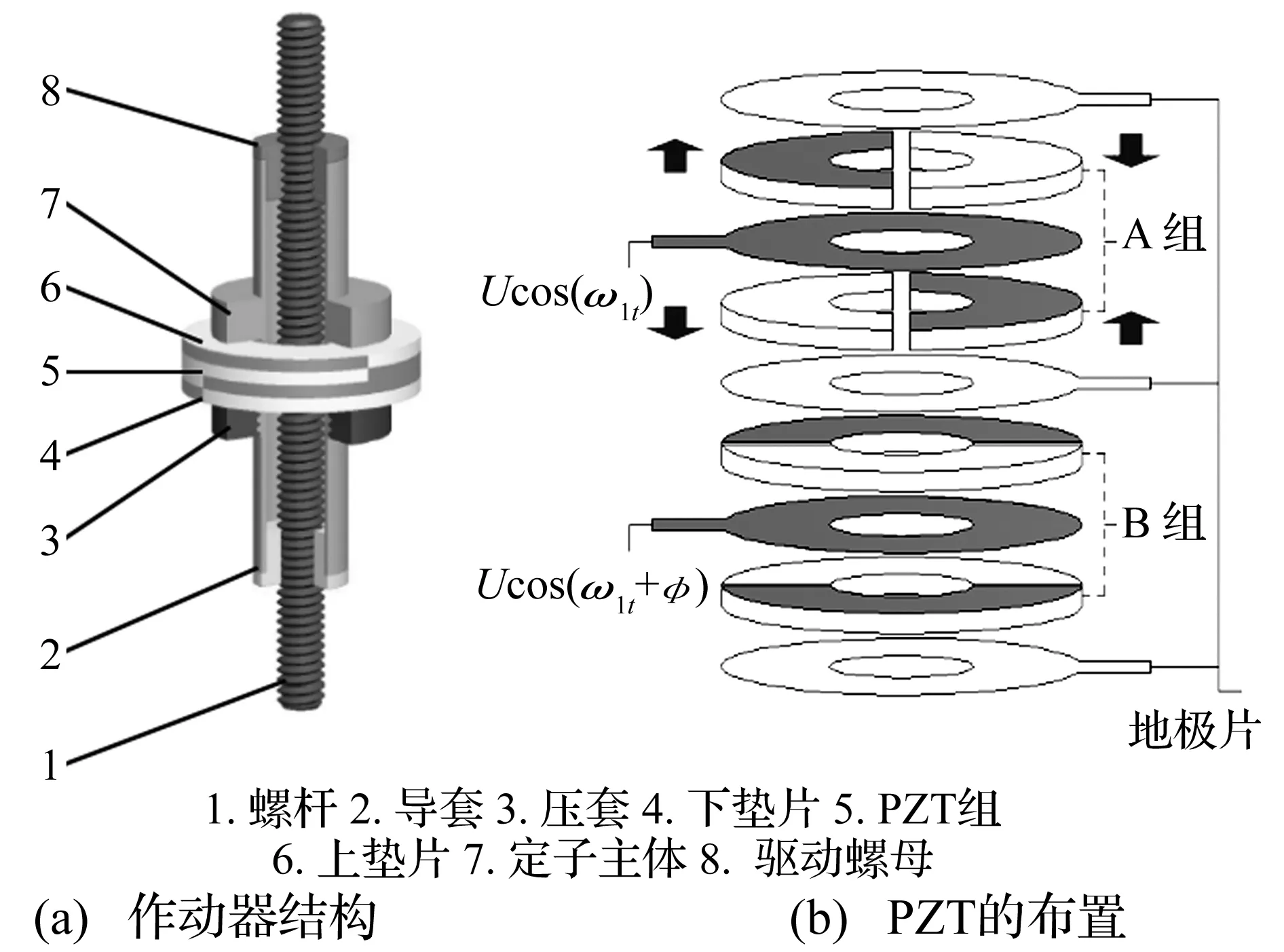
图1　压电作动器结构Fig.1 Structure of piezoelectric actuator

1.2工作原理

本文压电作动器的压套和定子主体上夹持部位的作用是：将压电陶瓷片组产生的交变应力转化为在细直梁上的交变力矩。为了便于理论分析，并考虑压电陶瓷片组、压套、定子主体的夹持部位三者的作用，本文对模型进行了简化：将压电陶瓷片组、压套、定子主体的夹持部位三者简化为作用在细直梁上的对称交变力矩，如图2所示。

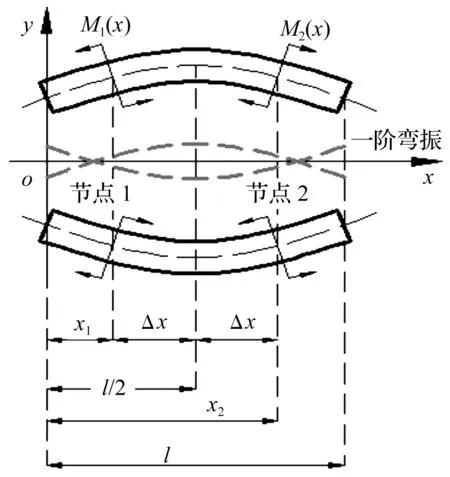
图2　激振力矩下自由梁的弯曲振动Fig.2 Bending vibration of free beam under driving torque

边界条件为两端自由的细直梁的固有频率[7]为

(1)

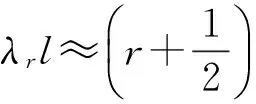
Yr(x)=Dr[coshλrx+cosλrx-

Er(sinhλrx+sinλrx)]

(2)

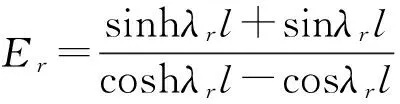
当交变力矩M1(x)作用在x=x1处时，梁的响应[7]为

y1(x,t)=

(3)

同理，当交变力矩M2(x)作用在x=x2处时，梁的响应为

y2(x,t)=

(4)

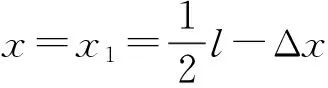
y(x,t)=y1(x,t)+y2(x,t)=

sinωnr(t-τ)dτ

(5)

由式(1)、(2)和(5)可知，对于结构尺寸和材料参数确定的梁，其响应位移仅受力矩大小和激振位置的影响。若将被预紧的压电陶瓷布置在合适的位置，施加交变激励电压，就会在细直梁上产生相应的激振力矩。

以A相为例，由于压电陶瓷的厚度hp很小，当施加Ucosω1t时，其平均电场强度为

(6)

分布的PZT元件组的应变可表示为

(7)

由第二类压电方程，可知

(8)

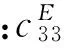
将式(6)和(7)代入式(8)，可得

(9)

至此，利用产生的交变应力，则可激励细直梁产生一阶弯振，如图3所示。当A、B两相同时激励时，定子就作合成弯曲振动(呼啦圈运动)，并在端面上形成一个波长的行波，使其上质点产生椭圆运动[8-9]。

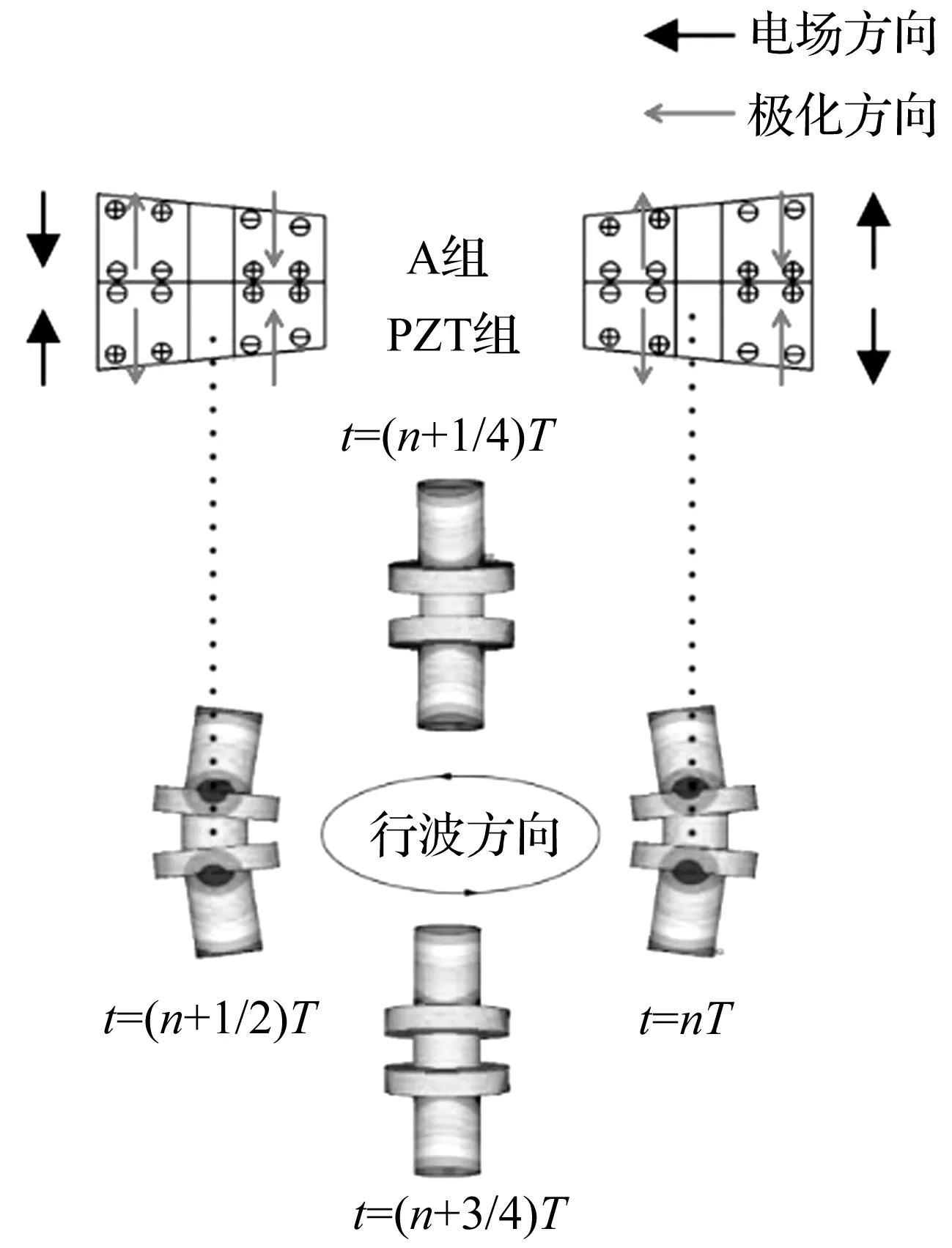
图3　工作原理示意图Fig.3 Work principle of actuator

由于作动器中驱动螺母紧固于定子端部，则螺纹内表面亦产生行波，通过接触摩擦力驱动螺杆转动，方向与行波方向相反。

2　作动器结构分析

为较好地模拟定子实际振动情况，本文借助于有限元软件ANSYS进行设计与仿真[10]。作动器定子结构参数如图4所示，水平方向D1～D3和竖直方向L1～L4共7个基本参数分别表示定子相应的直径和高度。定子的材料参数和尺寸参数见表1和表2。

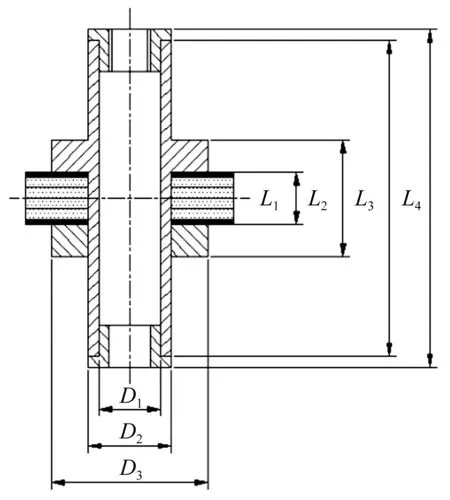
图4　作动器定子结构参数Fig.4 Structure parameters of actuator’s stator

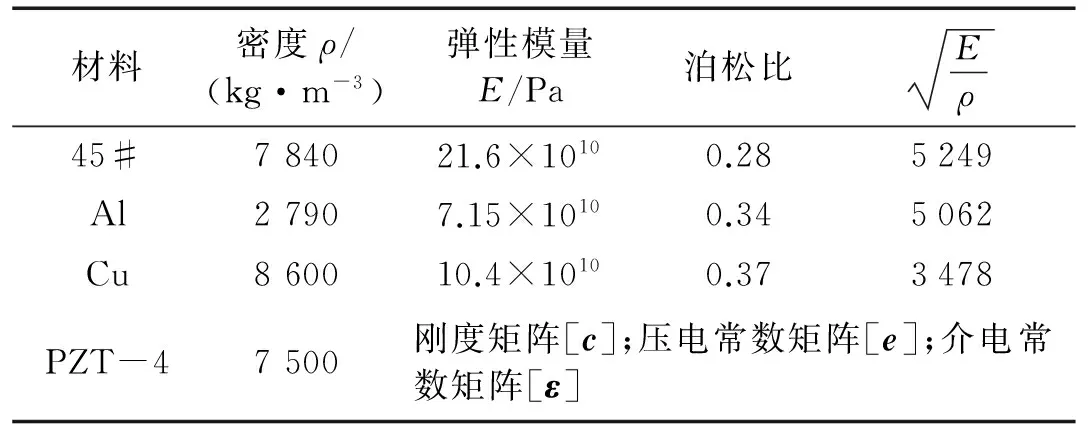
材料密度ρ/(kg·m-3)弹性模量E/Pa泊松比Eρ45#784021.6×10100.285249Al27907.15×10100.345062Cu860010.4×10100.373478PZT-47500刚度矩阵[c];压电常数矩阵[e];介电常数矩阵[ε]

其中

首先，分析定子材料及压套外径尺寸D3对一阶弯曲振动的影响。根据图4和表2，在ANSYS中建立定子有限元模型，定子中空内径D1为14 mm、垫片和PZT组总厚度L1为8 mm，夹持机构总长度L2为20 mm。本文借鉴现有的密切相关文献[4,11]，在ANSYS分析过程暂时不考虑定子与螺杆的接触问题，将边界条件设为为自由。压电陶瓷和金属基体的单元类型分别指定为SOLID98和SOLID45，通过Block Lanczos法分别对表1中三种金属材料的定子基体进行模态分析，选取一阶弯曲振动模态B01为工作模态。分析结果如图5所示，当定子材料保持不变时，减小压套外径D3，固有频率呈线性增大且端面振幅也有所增大，其中铝定子端面振幅增加幅度最大；当压套外径D3不变时，45钢和铝定子的固有频率接近，但铝定子的端面振幅较大，而铜定子的固有频率和端面振幅均最小。

表2　定子尺寸参数

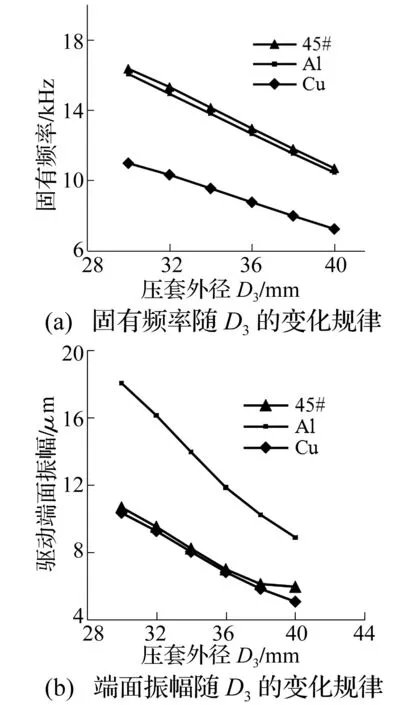
图5　材料参数及D3对一阶弯振的影响Fig.5 Influence of material parameters and D3 on the first order bending mode

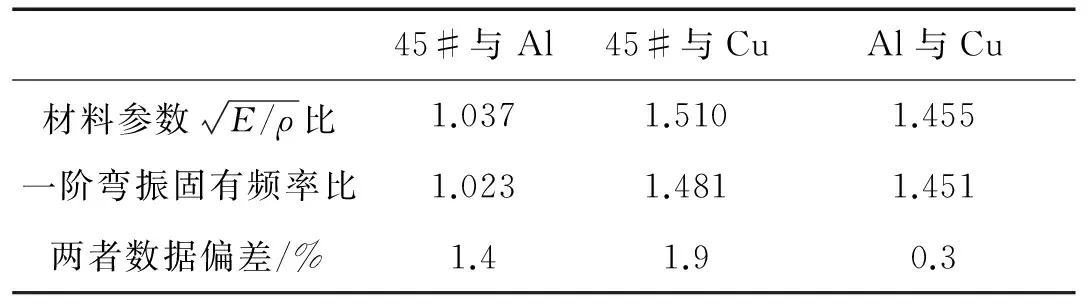
表3　材料参数对定子固有频率的影响

经过以上分析，本文采用铝质定子。为获得较大的端面振幅，应选取较小的压套外径尺寸，但压套外径过小会影响PZT组的稳定夹持，为保证夹持面积，选取压套外径D3为30 mm。

其次，分析定子内径D1对一阶弯振的影响，D1取值见表2，分析结果如图6。随定子内径的减小，定子壁厚增加，系统刚性增大，端面振幅逐渐下降，一阶弯振的固有频率逐渐增加但幅度很小。因此，不宜通过减小内径来调节定子频率，且会导致端面的振幅下降，影响驱动效率。此处取内径为14 mm，定子主体壁厚为1 mm，此时定子B01模态频率为16.051 kHz，振幅为18.051 μm。

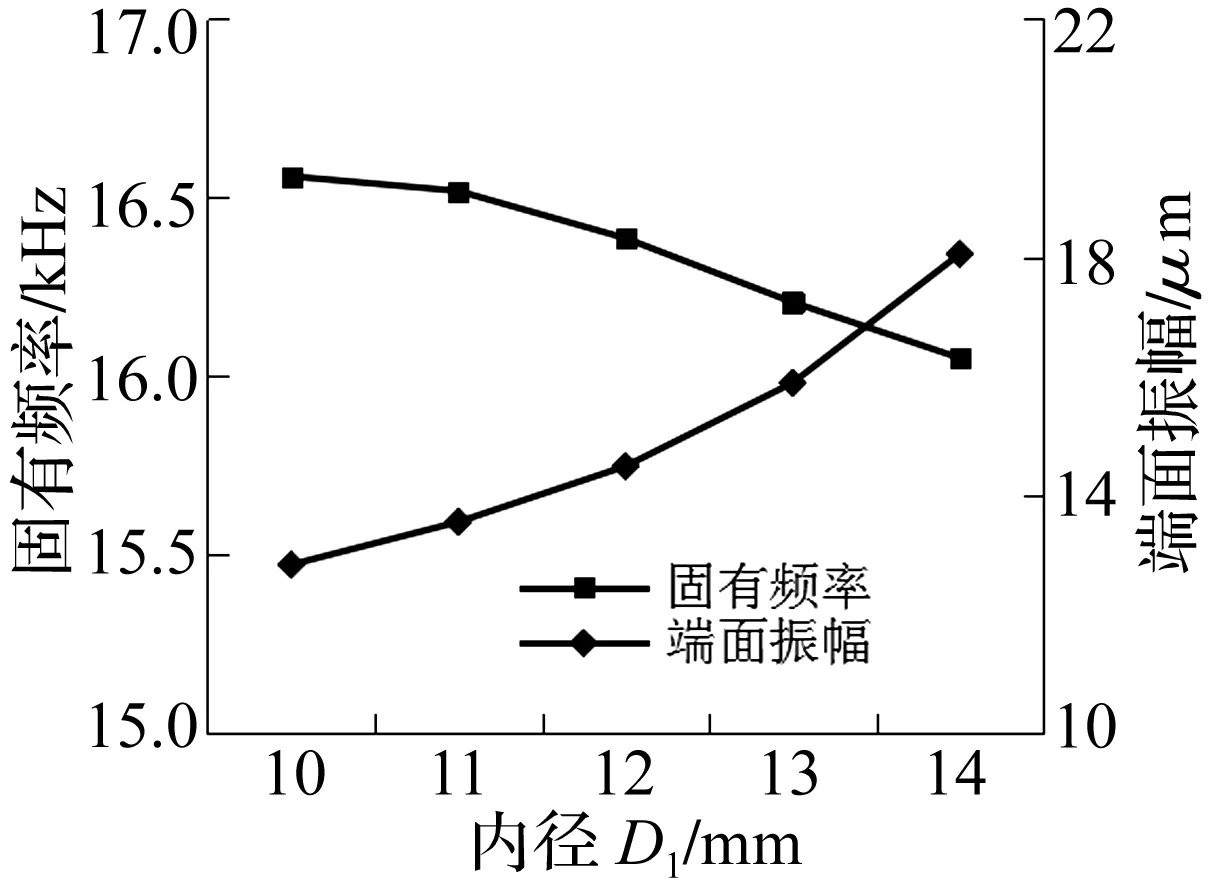
图6　定子内径D1对一阶弯振的影响Fig.6 Influence of D1 on the first order bending mode

最后，结合以上分析并考虑实际装配的可操作性，最终确定了作动器尺寸参数，如表4所示。

表4　定子基本尺寸参数(单位：mm)

3　试验研究

3.1定子模态实验

根据前文对材料和结构参数分析的结果，加工制作的作动器样机如图7所示。其中，压电陶瓷材料为PZT-4，尺寸为40 mm×16 mm×2 mm的环片。定子主体和压套材料均为硬铝，压套内螺纹为M18 mm×1.25 mm，厚度t2=6 mm，以保证预紧效果。为防止PZT因受力不均匀而损坏，装配时上下各配有1片40 mm×20 mm×0.5 mm的垫片。驱动螺母和导套的材料为45#，其边缘厚度t3=2 mm。输出轴为日本MISUMI公司FAB M8×1.25型精密螺杆。

图7　作动器样机Fig.7 Prototype of the actuator

利用Agilent 4294A型阻抗分析仪对双弯曲螺杆型压电作动器的样机定子进行扫频测试，定子B01模态的实测频率为15.8 kHz，略小于有限元计算结果(16.051 kHz)。其原因一是仿真计算采用的材料参数与实际的材料参数值会略有偏差；二是实际结构中定子主体和压套为螺旋副连接，而仿真分析时视定子为整体。

3.2作动器输出性能测试

为测试样机的主要性能，搭建如图8所示试验系统，包括任意波形发生器(RIGOL DG4102)、功率放大器(Tabor 9200A)、数字示波器(DP02024)、激光测微仪(Keyence LK-G5001V)以及推拉力计等。测试系统置于气浮隔振台上，样机、数显测力计、激光测量头分别固定在各自的测试支架上，中心高度调整为等高。激光测微仪记录转子直线位移，数显测力计记录转子的输出力。

图8　样机测试系统Fig.8 Test system of prototype

首先确认样机的有效驱动频率。图9为空载条件下，驱动电压300 V、相差90°时输出速度对驱动频率的关系。由图可知，驱动频率大于15.8 kHz且小于16.0 kHz时速度有所下降但相对比较平缓。因此，作动器的最佳频率范围应为15.8～16.0 kHz，最大空载速度约为1.146 mm/s。同时，测试中观察到，作动器启停特性较好，响应时间在各个频率点上约为20～40 ms不等。图10所示为启动响应时间的测试结果，在15.8～16.0 kHz区间响应最灵敏。停止响应的时间和趋势大体与启动过程一致。

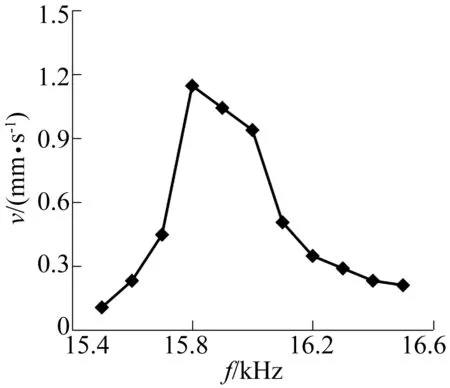
图9　速度与频率关系曲线Fig.9 Relationship between speed and frequency

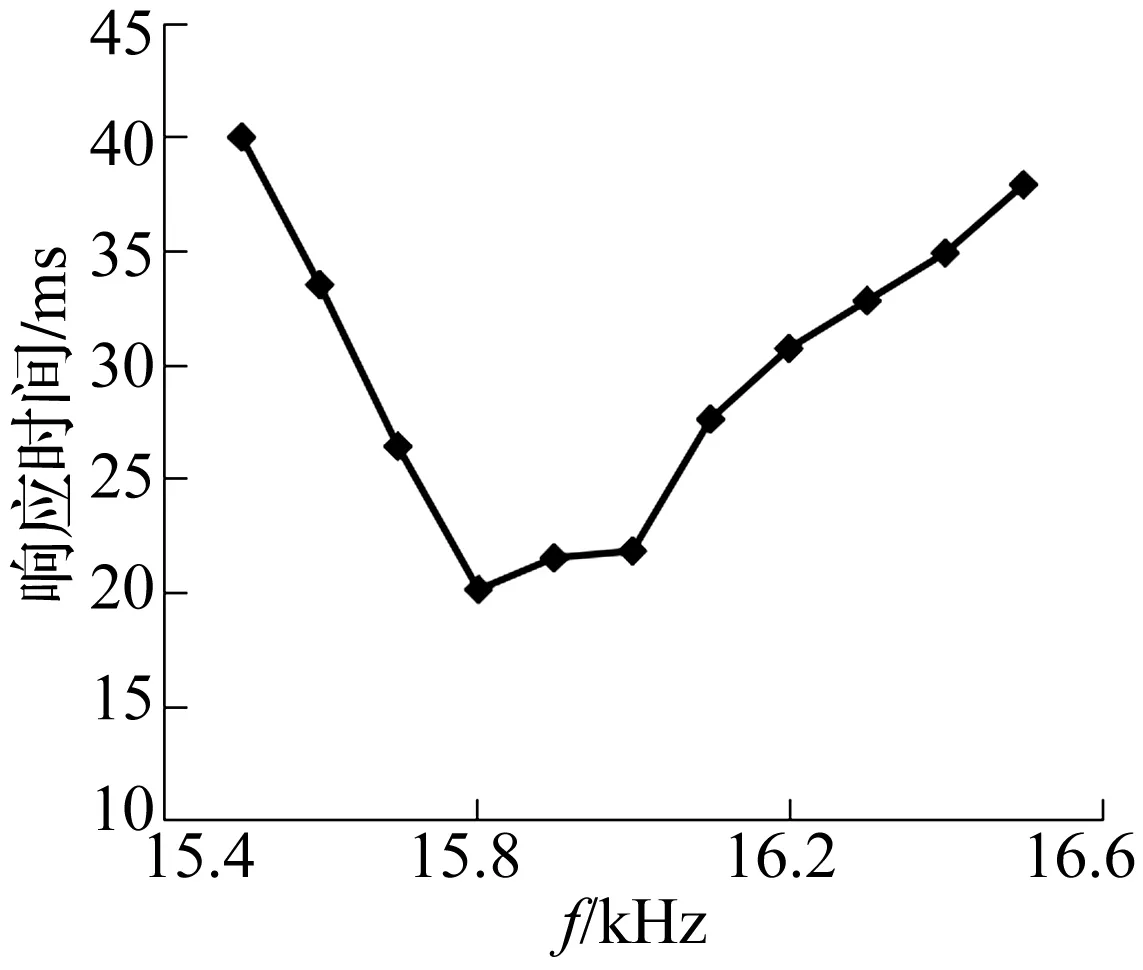
图10　响应时间与频率关系曲线Fig.10 Relationship between response time and frequency

其次考察速度和相差的关系。图11为作动器空载条件下，固定驱动电压和频率分别为300 V和15.8 kHz时，在0～180°范围内连续调节相差所测得的试验结果。显然，曲线近似为对称图形，与预期一致，最大速度出现在相差90°附近。因此，在高频段工作区间，如果调频调速电路复杂，也可以考虑通过调相的方式控制速度。

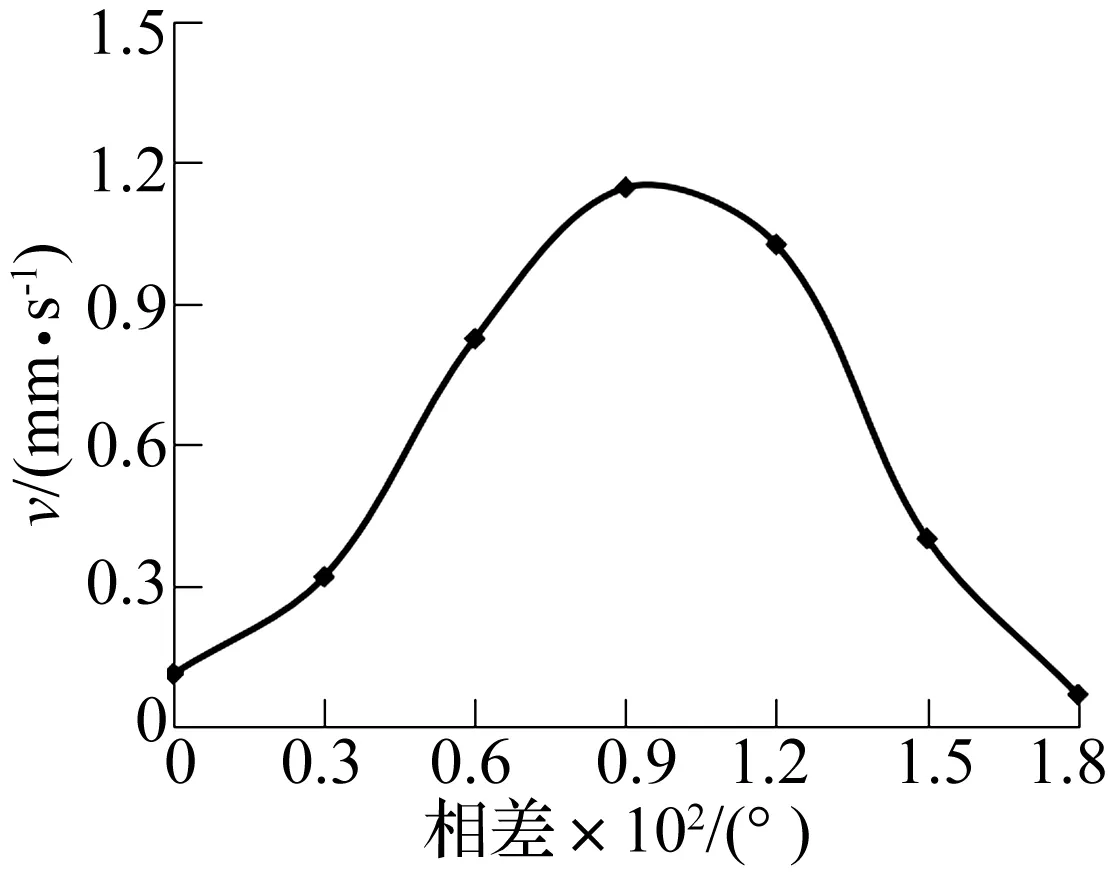
图11　速度与相差关系曲线Fig.11 Relationship between speed and phase difference

接下来，测试样机输出特性与驱动电压的关系。图12为作动器在15.8 kHz和相差90°条件下，所测得的速度以及输出力与激励电压的关系曲线。测试结果表明，作动器的速度和输出力均随驱动电压的增加而增大。当驱动电压低于100 V时，速度几乎为零，这是由于低压时定子驱动端面振幅过小，此时的接触摩擦力矩不足以驱动螺杆转动。在最大电压300 V下，作动器速度最高约1.146 mm/s，输出力约为2.5 N，力值偏小。

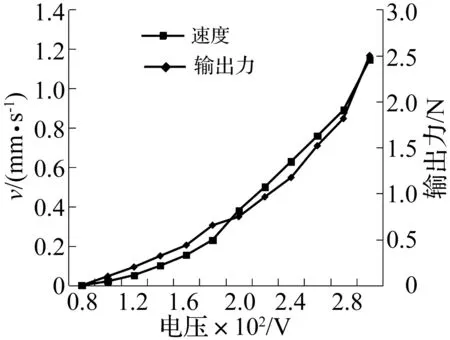
图12　速度和输出力与电压关系Fig.12 Influence of voltage on speed and output force

最后，测试作动器的机械特性。驱动电压、频率、相差均按照理想情况设置，考察作动器的带载能力，测试结果如图13所示。由图可知，作动器的机械特性近似为线性，速度随负载的增大而减小，轴向堵转力约为2.5 N。

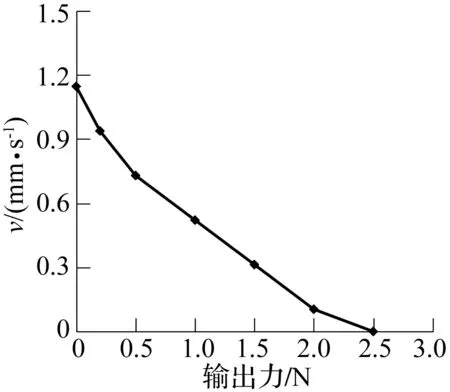
图13　速度与输出力关系曲线Fig.13 Relationship between speed and output force

与贴片式作动器相比，目前二者在力能指标方面仍处于同一量级，并未有实质性地提升。尽管如此，采用Kt换能方式设计的螺杆式作动器，至少在两方面存有优势：① 壁厚均匀，从根本上避免了多面体贴片式结构周向刚度不一致的问题；② 可以通过优化结构，进一步增加换能器数量以提高输入能量，而贴片式结构若要提高输入能量，无论是增大换能器面积还是厚度，都会同时带来定子刚度明显增加的问题，这方面在项目组上一阶段的研究中，做过相应的尝试[12]。因此，本文所采用的结构设计仍不失为一种值得继续探索的方式。

4　结　论

本文讨论了一种基于压电陶瓷Kt模态的双弯曲管式结构，探索了螺杆型作动器的另一种形式。主要结论如下：

(1)理论和仿真结果对比表明，将管式双弯曲定子视为细直梁进行分析和优化设计的方法是可信的；在此基础上，确定了双弯曲螺杆型压电作动器的基本结构并阐述了驱动原理；仿真计算了材料参数对定子固有频率和端面振幅的影响，其中，通过材料参数E/ρ比预估定子工作频率的方法对作动器设计有一定的借鉴意义。

(2)通过样机实测，作动器的最佳激振频率约为15.8 kHz，与设计频率基本一致；最大空载速度约为1.146 mm/s，堵转轴向力约为2.5 N，可以满足微操作/微装配等微细作业场合对执行器在力和速度方面的要求[13]。

[1] Henderson D A. Piezo ceramic motors improve phone camera auto focus and zoom[OL]. article in www. squiggle. com, 2005.

[2] Henderson D A. Ultrasonic lead screw motor: U.S. Patent 6,940,209[P].2005-9-6.

[3] Henderson D A. Simple ceramic motor... inspiring smaller products[J]. Stroke (mm), 2006,10:14-16.

[4] Zhang J T, Huang W Q, Zhu H, et al. Lead screw linear ultrasonic motor using bending vibration modes [J]. Transactions of Nanjing University of Aeronautics & Astronautics,2007,26(2)：89-94.

[5] 周铁英，张筠，陈宇，等.螺母型超声电机及其在透镜调焦中的应用[J].科学通报，2008，53(11)：1251-1256.

ZHOU Tie-ying，ZHANG Jun，CHEN Yu，et al. Nut-type ultrasonic motor and its application in the focusing lens [J]. Science Bulletin, 2008，53(11)：1251-1256.

[6] 陈维山，刘英想，石胜君.纵弯模态压电金属复合梁式超声电机[M].哈尔滨工业大学出版社,2011,12:62-63.

[7] 屈维德，唐恒龄，张益群. 机械振动手册.第二版[M].北京：机械工业出版社，2000,4:135-141.

[8] 黄卫清,马相林,董迎晖,等. 杆式行波超声电机运动机理的研究[J].振动与冲击,2004,23(2):48-51.

HUANG Wei-qing，MA Xiang-lin，DONG Ying-hui，et al. Researches on the mechanism of traveling wave type ultrasonic motor [J]. Journal of Vibration and Shock,2004,23(2):48-51.

[9] 赵淳生.超声电机技术与应用[M].北京：科学出版社，2007,2：34-36.

[10] 李怀勇. 新型杆式压电电机研究[D].秦皇岛: 燕山大学,2013.

[11] 郭向东．基于贴片式弯振模态超声电机驱动电气比例阀的研究[D] .哈尔滨：哈尔滨工业大学，2012．

[12] 华顺明,李鑫,楼应侯,等. 面向介观尺度制造的螺杆型压电作动器[J]. 纳米技术与精密工程,2014,12(4):300-305.

HUA Shun-ming，LI Xin，LOU Ying-hou，et al. Screw-Type Piezoelectric actuator applied in meso-scale manufacturing [J]. Nanotechnology and Precision Engineering, 2014,12(4):300-305.

[13] 沈飞,徐德,唐永建,等. 微操作/微装配中微力觉的测量与控制技术研究现状综述[J]. 自动化学报,2014(5):785-797.

SHEN Fei， XU De，TANG Yong-jian，et al. Review of measuring and control technology of microforce in micromanipulation and microassembly [J]. Acta Automatica Sinica，2014(5):785-797.

A screw type piezoelectric actuator with bi-directional bending vibrations

HUA Shun-ming1, MENG Yu-ming1,2, LOU Ying-hou1, LI Zhi-qiang1,2, LI Jia-lin1,2

(1. Ningbo Institute of Technology, Zhejiang University, Zhejiang 315100, China；2. School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China)

A screw-type piezoelectric actuator based on bidirectional bending vibrations of a piezoelectric metal compound beam was proposed, where each piezoelectric transducer worked with Kt mode. The structural form of the actuator was determined with the first order bending modal shape of a beam in space; secondly, the influences of stator’s material and structural parameters on the natural frequencies and ends’ amplitude of the stator were analyzed with ANSYS software. The influence of the material parameterE/ρon the first order natural frequency of the stator was especially discussed. Then, the structural sizes of the actuator were determined according to the analysis results, and the prototype of the actuator was madal. Finally, the main output characteristics of the prototype were tested. The results indicated that the actuator responds sensitively with the start-stop time of about 20 ms, the optimal excitation frequency is approximately 15.8 kHz, the maximum no-load speed and the maximum output axial force are 1.146 mm/s and 2.5 N, respectively under the excitation voltageVpp=300 V.

actuator; piezoelectric metal compound beam; bending mode; mechanical characteristics

10.13465/j.cnki.jvs.2016.13.002

国家自然科学基金(51275467);浙江省自然科学基金(LY16E050009)

2015-02-04修改稿收到日期：2015-07-09

华顺明 男，博士，教授，1972年生

TM359.5

A