基于无网格法梁结构多裂纹定量识别
2016-08-04罗志钢蒋占四王衍学向家伟
罗志钢, 蒋占四, 王衍学, 向家伟
(1. 桂林电子科技大学 机电工程学院,广西 桂林 541004; 2.温州大学 机电工程学院,浙江 温州 325035)
基于无网格法梁结构多裂纹定量识别
罗志钢1, 蒋占四1, 王衍学1, 向家伟2
(1. 桂林电子科技大学 机电工程学院,广西 桂林541004; 2.温州大学 机电工程学院,浙江 温州325035)
研究基于无网格法的悬臂梁结构多裂纹定量识别方法。通过局部加权残量法将裂纹以虚拟边界融入离散系统方程,建立多裂纹梁结构动力学模型,获得定量识别正问题数据库。结合曲率模态法先找到裂纹位置,再以实测频率作为反问题输入利用粒子群法反演寻优从而定量预测出裂纹的损伤程度。数值仿真表明,该方法前处理简单,适合用来模拟非连续裂纹问题,为结构多裂纹识别提供了新途径。
无网格法;多裂纹;识别
结构的裂纹是一种常见的损伤形式,在长期交变应力和冲击载荷的作用下,容易引起裂纹扩展从而导致结构破坏,引起安全事故。因而对结构是否产生裂纹并对其位置和损伤程度进行及时诊断和评估[1]在工程实践中具有重要意义。
近年来国内外对含裂纹的结构进行了大量分析研究,比如基于小波包与倒频谱分析的裂纹诊断方法[2], 基于网格式支持向量机算法的转轴裂纹故障诊断[3]。这些方法在诊断裂纹故障上取得了较好的效果,但准确性有待提高,尤其多裂纹问题存在困难。在用基于模型的方法分析裂纹方面以有限元法最为普遍。陈雪峰等[4-6]将小波有限元引入到裂纹故障诊断。利用小波多尺度多分辨的特性,针对求解问题的精度要求,可采用不同类型和尺度的小波基函数,因而在处理结构裂纹奇异性问题具有一定的优越性。文献[5]在悬臂梁裂纹识别中利用6阶Daubechies小波基单元,取得了良好的计算结果。但是Daubechies小波无显式表达式,用于构造小波单元时必须计算联系系数,计算复杂。
用有限元法模拟裂纹问题时,由于裂纹尖端的应力奇异性和裂纹的动态扩展往往需要对网格细化或网格的重新划分,特别在多裂纹问题求解中,网格的大量重构不仅降低了模型的计算精度,而且增加了计算成本。
无网格法解决了传统基于网格的数值方法缺点,它不存在类似有限元中单元边界要始终和结构内部不连续边界(裂纹)保持一致的问题,避免了网格重构带来的数值困难。本文通过无网格PETROV-GALERKIN法[7]对多裂纹悬臂梁结构进行研究。从加权残量法出发将裂纹以虚拟边界引入,建立多裂纹结构的正问题动力学模型;结合前人研究的曲率模态法[8-11]确定裂纹位置的基础之上,将反问题实测系统的前三阶固有频率作为输入,利用粒子群优化(PSO)方法反演寻优定量预示该位置的损伤程度。通过悬臂梁双裂纹诊断试验,验证该方法的有效性。
1 MLS形函数
根据移动最小二乘法,在域Ω中任一点的近似表达式为:
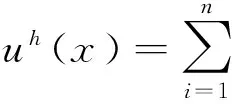
(1)
式中:φi为对应于点x的支持域中n个节点的MLS形函数;节点i的形函数φi(x)为:
(2)
A(x)为加权力矩矩阵,定义为:
(3)
矩阵B(x)为:
(4)
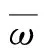
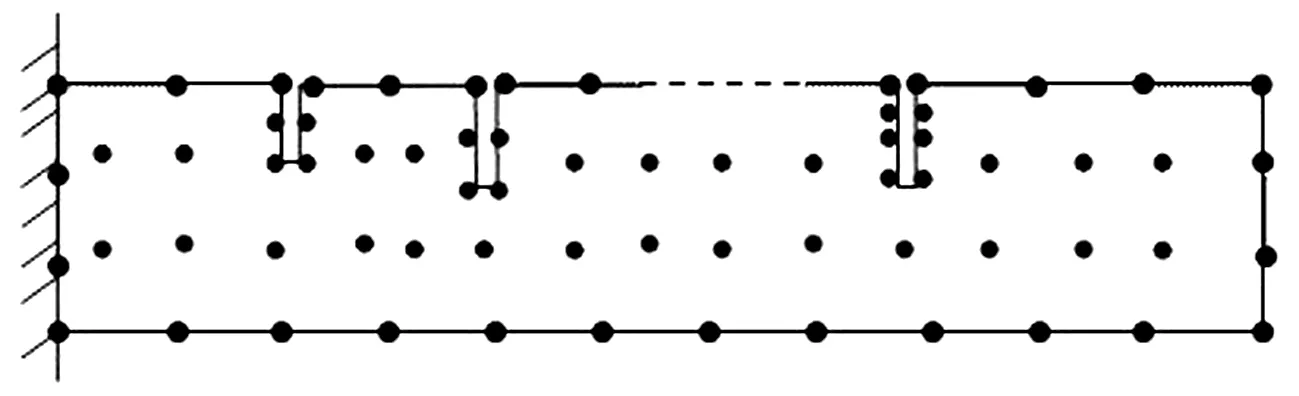
2 多裂纹悬臂梁的无网格分析
图1,2分别多裂纹悬臂梁及其无网格模型。其中L是梁的长,L1,L2…Li;a1,a2…ai分别为相应裂纹对应的位置和深度。假定均匀截面的梁的自由振动方程为:
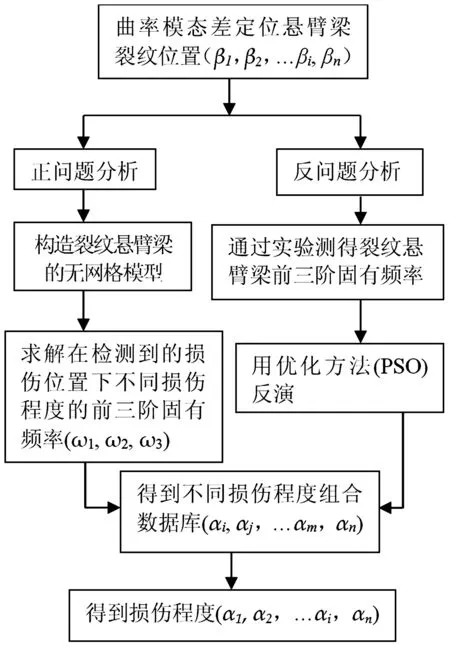
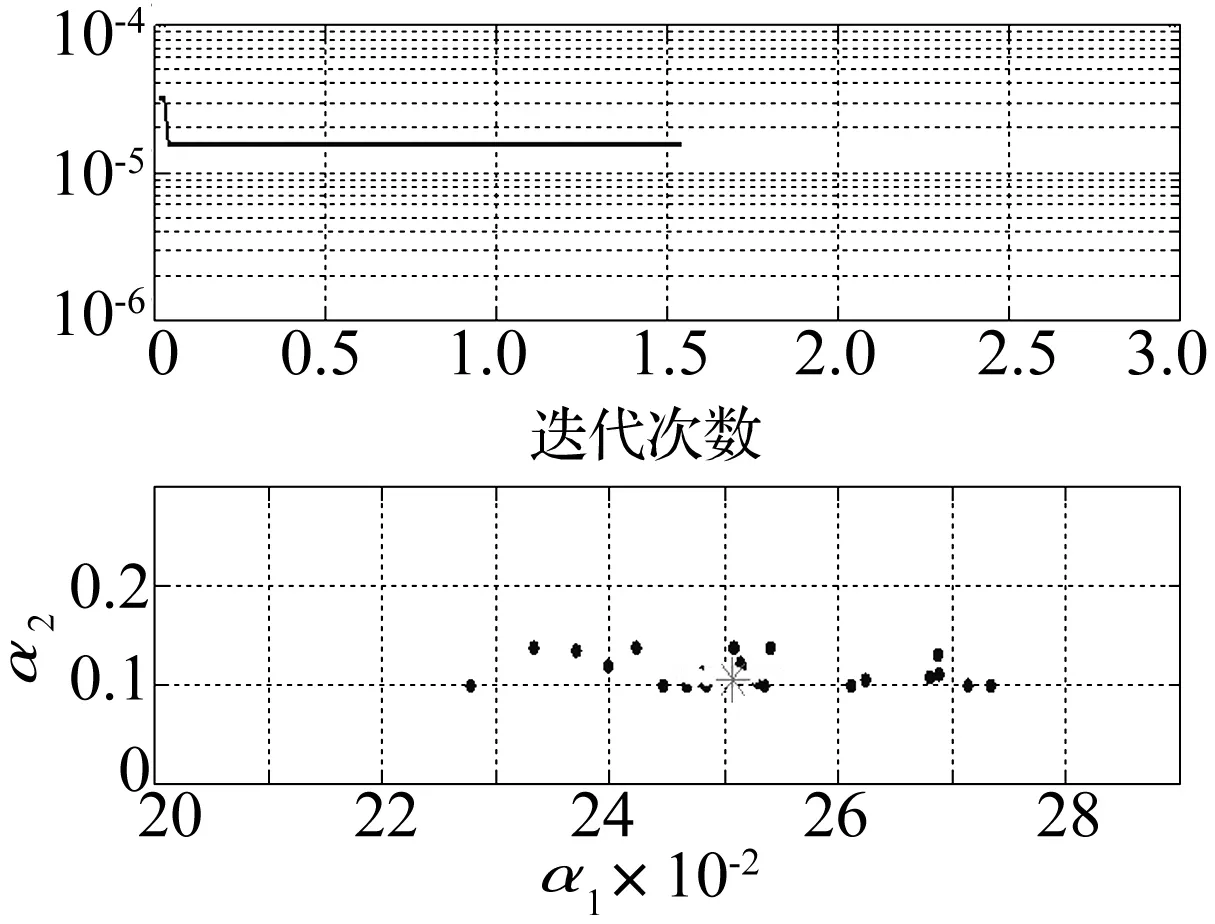
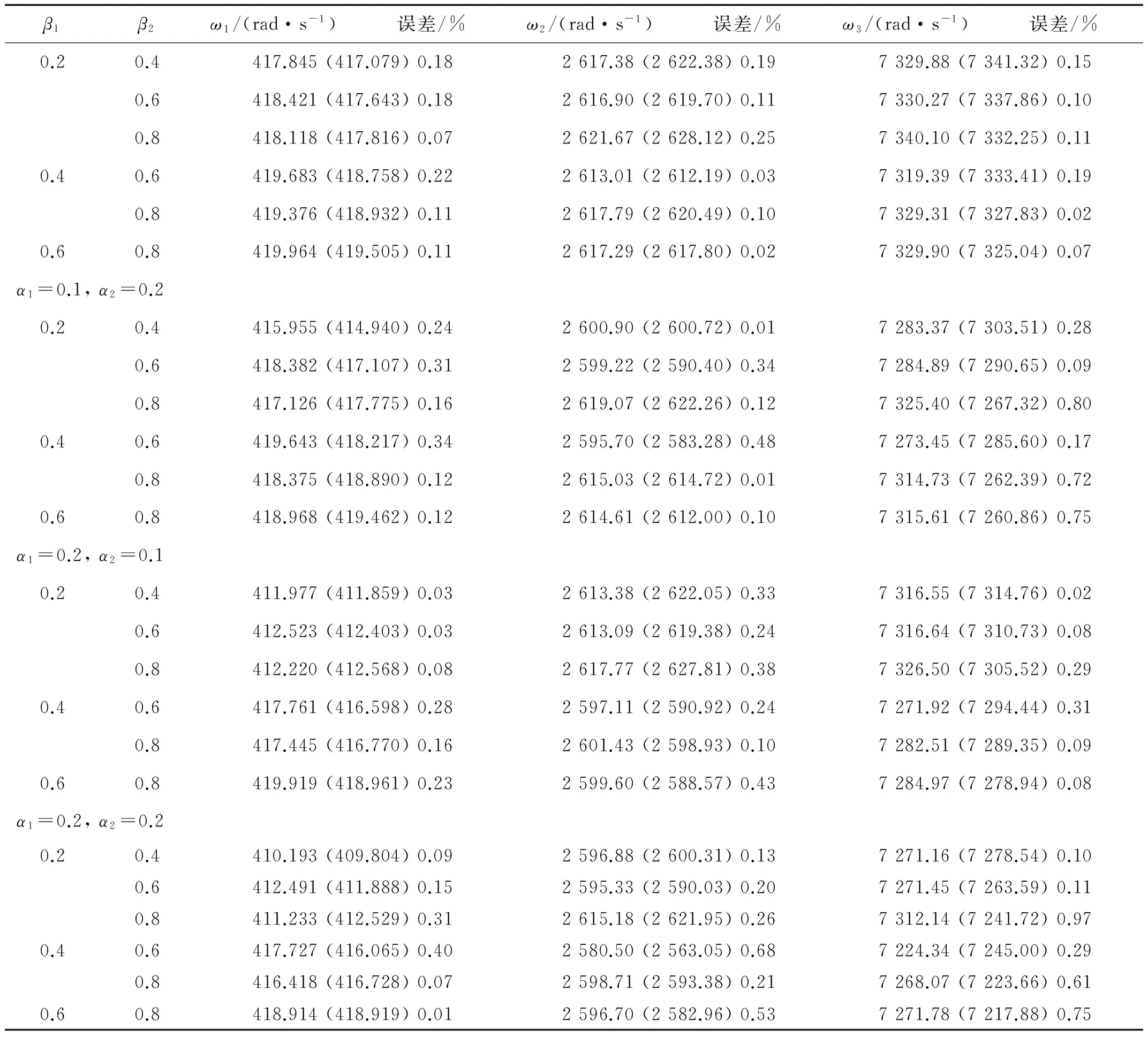
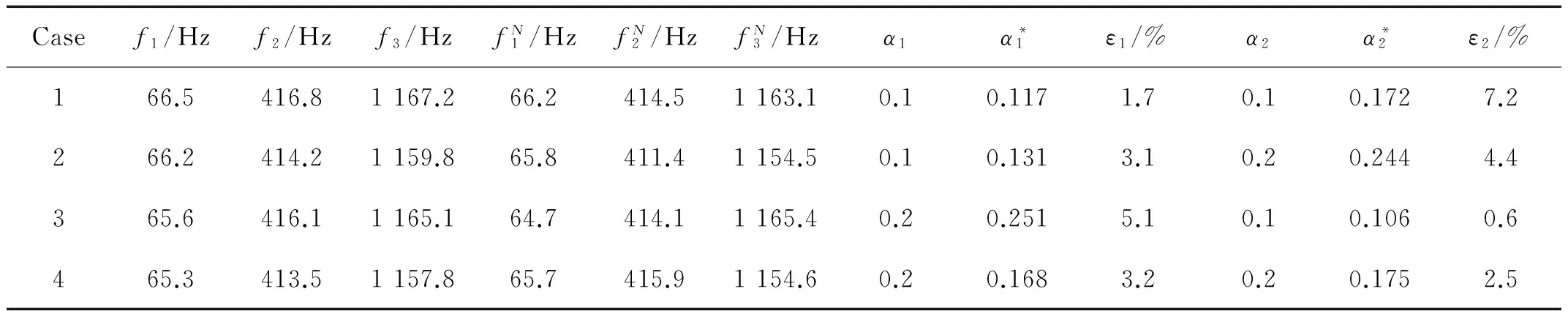
0 (5) 式中:u(x,t)是梁的轴向横位移,ρ是梁的密度,A是梁的截面面积,EI是梁的弯曲刚度,将u(x,t)空间坐标进行离散化: u(x,t)=u(x)eiwt=ueiwt (6) 将式(6)代入等式(5)化简为: EIu″″=ω2ρAu0 (7) 这样u=u(x)变成只是空间坐标的函数,ω是自然频率。 图1 多裂纹悬臂梁模型Fig.1 Multiple cracks cantilever model 图2 多裂纹悬臂梁无网格模型Fig.2 Multiple cracks cantilever meshless model 边界条件为: u(x)=u0在Γu上, (8) M=M0在ΓM上, V=V0在ΓV上 (9) Γu∩ΓV=Ø,Γθ∩ΓM=Ø (10) 其中:M是弯力矩,V是剪切力,Γu,Γθ,ΓM,ΓV,是边界上的位移,转角,弯力矩,剪切力。在裂纹处,连续条件为: (11) (12) (13) 不连续条件为转角[12]: (14) 式中:xc为裂纹处的坐标,λ表示裂纹所在部位梁等效为无质量扭转弹簧的影响系数,λ能被表示成裂纹深度a和梁高h的函数[13-14]: λ=5.346hg(ξ) (15) 其中: g(ξ)=1.862 4ξ2-3.95ξ3+16.375ξ4- 37.226ξ5+76.81ξ6-126.9ξ7+ 172ξ8-143.97ξ9+66.56ξ10 (16) (17) 采用局部加权残量法[7,15]: (18) (19) (20) (21) 由力矩M和剪力V的关系为: M=EIu″;V=-EIu‴ (22) 将式(22)和边界条件式(9)代入式(21)得: (23) (24) 由式(11)~(14)可知在裂纹处悬臂梁的位移和它的二阶,三阶导数是连续的,而一阶导数不连续,即: 由式(24)可得: (25) 将形函数式(1)和权函数代入式(25),由此可得到系统模态方程: (K+Kc-ω2M)U=F (26) 式中:K是悬臂梁系统不含裂纹时的刚度矩阵,Kc是对应裂纹处的等效刚度矩阵,M是系统的质量矩阵,F是外界所施加的载荷。因此,系统节点的刚度矩阵为: 〗(27) 裂纹处的等效刚度矩阵为: (28) 系统节点的质量矩阵为: (29) 系统节点载荷为: (30) 若为任意数量的裂纹(28)可写为: (31) 基于无网格法的裂纹识别流程如下(见图3):首先利用曲率模态法确定裂纹的相对位置(β1,β2,…βi, βn);然后正反问题结合并利用粒子群优化(PSO)算法来估算该位置的损伤程度(α1,α2,…αi,αn)。该方法结合了曲率模态法[8-11]在奇异性分析方面的优势,同时降低了多裂纹参数反演寻优的维度,简化了计算。 3.1裂纹损伤位置识别 首先用实验模态分析(EMA)测量获得裂纹梁的第m阶模态Ym,并计算得到其模态曲率Vm。通过中心差分法近似得到该点的模态曲率[16]如下: (32) 式中:hc为相邻两点的距离,j表示空间不同位置的点,Ym,j-1,Ym,j,Ym,j+1,是Ym上三个连续的点。裂纹位置可以从模态曲率的外观上确定,如果有突变或峰值出现,则该位置有损伤存在,从而确定损伤位置β1,β2,…βi,βn。 3.2裂纹损伤程度求解 从图3可知,在正问题分析中,利用无网格局部PETROV-GALERKIN法,求得振动特征方程得到了裂纹梁自由振动的固有频率ωm(m=1, 2, 3, …), 即对于给定的裂纹相对位置β,求解不同α相关的各阶总体振动频率ωm=ω(α1,α2,…αj,αn)可得到裂纹梁定量识别数据库。 在反问题分析中,通过实测的ω*反演优化求解出裂纹的相对深度。现在构造如下目标函数(33)。 (33) 式中:ωj为数值计算的不同裂纹相对深度组合的数据库,ωj*表示实测频率。利用粒子群优化方法(有关粒子群优化方法详见文献[18])从数据库中寻求最优解以获得真实裂纹的参数(α1,α2,…αi,αn)。 曲率模态差定位悬臂梁裂纹位置(β1,β2,…βi,βn) 图3 裂纹诊断流程图Fig.3 Crack diagnosis flow chart 4.1裂纹梁固有频率计算 为了验证该算法的有效性,以文献[17]中的双裂纹悬臂梁进行验证,参数如下:弹性模量E=210 GPa,密度ρ=7 860 kg/m3,悬臂梁有效长度L=0.5 m,横截面高度H=0.02 m,宽度B=0.012 m。 用本文无网格法计算双裂纹梁的前三阶固有频率并与文献[17]中的频率对比,列于表1。其中α表示裂纹相对深度,β表示裂纹相对位置,ω表示固有频率,括号内数据是来自文献[17]中的频率。可以看出该方法求得固有频率误差小于1%,满足精度要求。为裂纹识别打下了基础。 4.2裂纹识别仿真 利用曲率模态法先找到双裂纹悬臂梁的裂纹位置β1,β2,然后以该裂纹位置实测频率ω*作为输入,利用PSO[18]算法寻优求解出与输入值相差最小的样本点,从而获得该裂纹位置相应的损伤程度α1,α2。 为了模拟实测频率中含有噪声信号的影响,现加入±2%高斯白噪声[19](WGN)后的固有频率为: (34) 由表2可知,在不同的裂纹工况下,定量诊断的两个裂纹的相对深度α误差在8%以内。表明此无网格法在低水平的噪声环境下,可以可靠地进行裂纹梁的定量诊断。 图4 双裂纹位置模态曲率形状图Fig.4 Two crack locations detection using the mode shape curvature 图5 粒子群优化(PSO)的收敛进程和对应识别两个裂纹的相对深度Fig.5 Convergence process of PSO and identify the two corresponding relative crack depths 图6 实验装置图Fig.6 Experimental setup 表1 双裂纹悬臂梁前三阶固有频率 表2 四组裂纹工况的识别结果 图7 二阶模态形状与曲率Fig.7Thesecondmodeshapeandcurvemodeshape图8 PSO识别对应位置裂纹相对深度Fig.8PSOidentifycorrespondingrelativecrackdepths (1) 提出一种用于梁结构多裂纹定量识别的无网格法。通过局部加权残量法将裂纹以虚拟边界引入,从而将裂纹融入系统振动特征方程中,构造悬臂梁裂纹参数定量识别正问题模型以获得裂纹诊断数据库;并通过实测的裂纹系统固有频率,结合曲率模态法先定位再利用粒子群优化(PSO)算法反演数据库以寻最优解从而定量识别出悬臂梁系统裂纹的相对深度。 (2) 数值仿真研究表明:基于无网格法对梁结构多裂纹定量识别方法切实可行,且只需要节点信息,前处理简单,因而非常适合用来模拟非连续(裂纹)问题,为结构多裂纹识别提供了新途径。 [1] 张敬芬,赵德有. 工程结构裂纹损伤振动诊断的发展现状和展望[J].振动与冲击, 2002, 21(4): 22-26. ZHANG Jin-fen, ZHAO De-you. The current status and future development of damage diagnosis of vibration engineering structural crack [J]. Journal of Vibration and Shock, 2002, 21(4): 22-26. [2] 罗毅,甄立敬. 基于小波包与倒频谱分析的风电机组齿轮箱齿轮裂纹诊断方法[J].振动与冲击,2015,34(3):210-214. LUO Yi,ZHEN Li-jing. Diagnosis method of turbine gearbox crack based on wavelet packet and cepstrum analysis[J]. Journal of Vibration and Shock, 2015, 34(3): 210-214. [3] 袁胜发 李秀琼. 基于网格式支持向量机算法的转轴裂纹故障诊断[J].振动与冲击, 2009, 28(9): 155-158. YUAN Sheng-fa LI Xiu-qiong. Shaft crack fault diagnosis based on grid support vector machines[J]. Journal of Vibration and Shock, 2009, 28(9): 155-158. [4] 陈雪峰, 向家伟, 董洪波, 等. 基于区间 B 样条小波有限元的转子裂纹定量识别[J]. 机械工程学报,2007,43(3):123-127.CHEN Xue-feng, XIANG Jia-wei, DONG Hong-bo, et al. Quantitative identification of rotor cracks based on finite element of B-SPLINE wavelet on the interval[J]. Chinese Journal of Mechanical Engineering, 2007,43(3):123-127. [5] 李兵, 陈雪峰, 何正嘉. 基于小波有限元的悬臂梁裂纹遗传优化辨识[J]. 振动与冲击, 2009, 28(12): 27-29. LI Bin, CHEN Xue-feng, HE Zheng-jia. Genetic optimization identification of Cantilever cracks based on finite element of wavelet [J]. Journal of Vibration and Shock, 2009, 28(12): 27-29. [6] Xiang J W, Jiang Z S, Wang Y X,et al. Study on damage detection software of beam-like structures[J]. Structural Engineering and Mechanics,2011,39(1):77-91. [7] Atluri S N, Zhu T. A new meshless local petrov-galerkin approach in computational mechanics[J]. Computational Mechanics,1998,2:117-127. [8] 彭华,游春华,孟勇. 模态曲率差法对梁结构的损伤诊断[J]. 工程力学,2006, 23(7): 49-53. PEN Hua, YOU Chun-hua, MENG Yong. Damage diagnosis of beam structures by modal curvature difference method [J]. Engineering Mechanics, 2006, 23(7): 49-53. [9] 何钦象, 杨智春, 姜峰, 等. 薄板损伤检测的高斯曲率模态差方法[J]. 振动与冲击, 2010, 29(7): 112-115. HE Qin-xiang, YANG Zhi-chun, JIANG Feng, et al. Damage detection for an elastic thin plate based on Gauss curvature modal difference [J]. Journal of Vibration and Shock, 2010, 29(7): 112-115. [10] Wang Y F,Liang M, Xiang J W. Damage detection method for wind turbine blades based on dynamics analysis and mode shape difference curvature information[J]. Mechanical Systems and Signal Processing,2014, 48(2): 351-367. [11] Ravi Prakash Babu K, Durga Prasad G. Crack detection in beams from the differences in curvature mode shapes[J]. Journal of Structural Engineering, 2012, 39(2): 237-242. [12] Rizos P F, Aspragatos N, Dimarogonas A D. Identification of crack location and magnitude in a cantilever beam from the vibration modes[J]. Journal of Sound and Vibration,1990,138(3): 381-388. [13] Zheng D Y, Fan S C. Natural frequency changes of a non-uniform beam with multiple cracks via modified Fourier series[J]. Journal of Sound and Vibration,2001,242(5):701-717. [14] 何永勇,褚福磊,郭丹,等.基于遗传算法的旋转机械转子裂纹识别的研究[J].机械工程学报,2001,37(10):69-74. HE Yong-yong, CHU Fu-lei, GUO Dan, et al. Research on rotating machinery rotor cracks identification based on genetic algorithm [J]. Chinese Journal of Mechanical Engineering, 2001,37(10): 69-74. [15] Fan S C, Sheng N. Meshless formulation using NURBS basis functions for eigenfrequency changes of beam having multiple open-cracks[J]. Journal of Sound and Vibration, 2004, 269(3):781-793. [16] Pandey A K, Biswas M, Samman M M.Damage detection from changes in curvature mode shapes [J]. Journal of Sound and Vibration,1991,145(2): 321-332. [17] Lee J. Identification of multiple cracks in a beam using natural frequencies[J]. Journal of Sound and Vibration,2009,320:482-490. [18] Birge B. PSOt-a particle swarm optimization toolbox for use with Matlab. Proceedings of the 2003 IEEE Swarm Intelligence Symposium (SIS03). [19] Suk M,Gillis D. Effect of mechanical design of the suspension on dynamic loading process [J] Microsystem Technologies,2005,11(8/9/10):846-850. Multi-crack detection of beam structures based on meshless method LUO Zhi-gang1, JIANG Zhan-si1, WANG Yan-xue1, XIANG Jia-wei2 (1. College of Mechanical and Electronic Engineering, Guilin University of Electronic Technology, Guilin 541004, China;2. College of Mechanical and Electronic Engineering, Wenzhou University, Wenzhou 325035, China) Multi-crack of a cantilever beam structure were detected based on the meshless method. With the local weighted residual method, cracks were taken as virtual boundaries to be integrated into a discrete system’s equations to build a multi-crack beam dynamic model and acquire a data base for identifying quantitatively a positive problem. Combined with the curvature modal analysis method, the crack positions were found. The measured frequencies were taken as inputs, the particle swarm optimization method was used for the optimization of an inverse problem to predict quantitatively the damage level of cracks. Namerical simulations showed that the proposed method is simple and suitable for simulating non-continuous crack problems, and it provides a new way for detecting multi-crack of structures. meshless method; mult-crack; identification 10.13465/j.cnki.jvs.2016.13.033 国家自然科学基金(51565008;51575400);广西制造系统与先进制造技术重点实验室开放课题(14-045-15-009Z);桂林电子科技大学研究生创新项目(YJCXS201506) 2015-05-20修改稿收到日期:2015-07-01 罗志钢 男,硕士生,1987年生 蒋占四 男,博士,副教授,1977年生 E-mail:jiangzhansi@gmail.com TU223;O346.1 A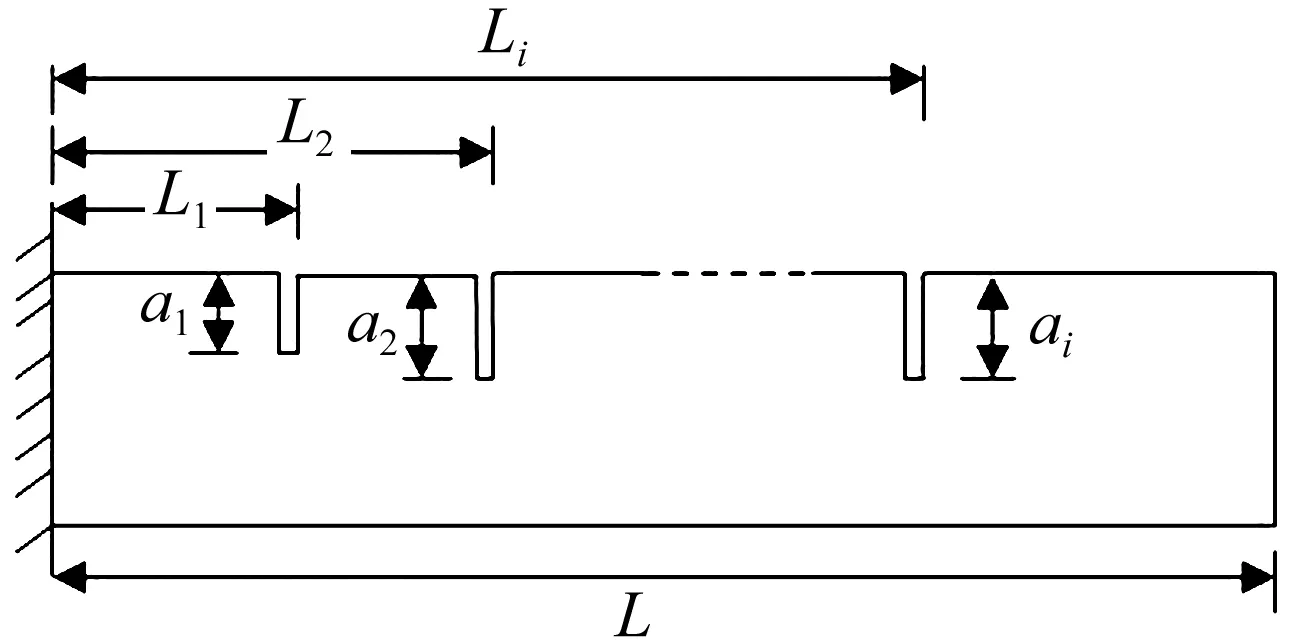
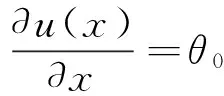

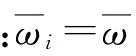
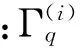
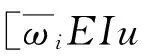
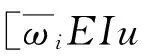
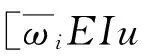
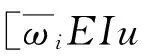
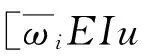
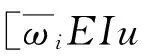
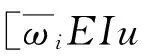
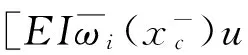
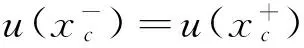
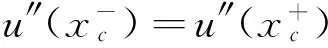

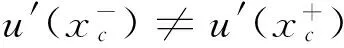
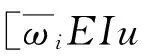
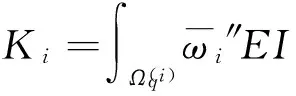
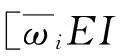
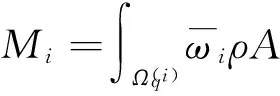
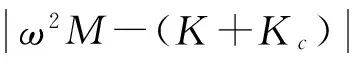
3 多裂纹诊断方法
4 数值仿真


5 实验研究



6 结 论
