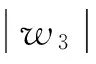基于振动控制的多楔带附件驱动系统优化
2016-08-04王红云曾祥坤赵季勇
王红云, 曾祥坤, 向 英, 赵季勇
(1.广东技术师范学院 汽车学院,广州 510641;2.广东技术师范学院 电子与信息学院,广州 510641;3.山东美晨科技股份有限公司,山东 诸城 262200)
基于振动控制的多楔带附件驱动系统优化
王红云1, 曾祥坤1, 向英2, 赵季勇3
(1.广东技术师范学院 汽车学院,广州510641;2.广东技术师范学院 电子与信息学院,广州510641;3.山东美晨科技股份有限公司,山东诸城262200)
建立了考虑带弯曲刚度的多楔带附件驱动(Serpentine Belt Accessory Drive,SBAD)系统梁耦合振动模型。以某三带轮SBAD系统为对象,计算分析带拉伸刚度、弯曲刚度、带线密度对带段横向振动、带动张力和张紧臂摆角等振动性能的影响;以上述振动性能构建目标函数,以带拉伸刚度、张紧器弹簧刚度和张紧臂长为设计变量对SBAD系统进行优化;最后在以上优化结果的基础上,通过降低带弯曲刚度,进一步改进SBAD系统的振动特性。
多楔带附件驱动系统;耦合振动模型;优化设计;振动控制
顺应汽车小型化、轻型化的发展,装有张紧器的多楔带附件驱动(Serpentine Belt Accessory Drive,SBAD)系统被发动机生产厂家广泛采用。与其它附件驱动系统比较,SBAD系统结构简单,附件(包括发电机、空调压缩机、动力转向泵、水泵、机油泵等)布置紧凑,传递功率大,振动和噪声小。
SBAD系统的振动模式主要有带段的横向振动和带轮、张紧臂的旋转振动。振动加速皮带磨损,影响附件性能和工作可靠性,进而影响整机、整车的技术指标,严重时还会导致SBAD系统运动失效和损坏。控制SBAD系统振动一直是国内外学者研究的重要内容之一。
Beikmann等[1-2]建立了SBAD系统旋转振动模型,研究了系统旋转振动性能。考虑带弯曲刚度,Kong[3]建立了3带轮SBAD系统梁耦合振动模型,研究了系统参数对带段横向振动的影响。近年来,优化设计方法被越来越多地应用到SBAD系统设计中。劳耀新等[4-5]以SBAD系统基频最小为目标,对张紧臂长进行优化设计。张智等[6]以带-轮间的滑移率最小为目标,对带线密度、带-轮间摩擦因数进行优化设计。王象武等[7]以带动张力波动幅值、带段初始张力和张紧臂摆角最小为目标,对张紧臂安装角、张紧臂长、张紧器刚度、张紧器阻尼进行优化设计。文献[8]以张紧臂摆角、单向离合器弹簧扭矩和带-轮间的滑移率最小为目标,对单向离合器弹簧刚度、附件轴转动惯量进行优化设计。作者在文献[9]中以张紧器有效系数最大、带段最大横向振动幅值最小为目标,对张紧器刚度、张紧臂长、张紧臂安装角进行优化设计,结果显示优化后的SBAD系统各带段横向振动幅值均有降低。
文献[4-7,9]在将张紧器参数、带参数作为优化对象对SBAD系统进行优化时,均将两者分开考虑。为此,文中将两者同时作为优化变量来对SBAD系统进行优化设计。
文中首先建立了考虑带弯曲刚度的n带轮SBAD系统梁耦合振动模型;研究了带参数(带拉伸刚度、弯曲刚度和带线密度)对SBAD系统振动性能(带段横向振动、带动张力和张紧臂摆角)的影响;接着以带段横向振动、带动张力、张紧臂摆角最小为目标,对带拉伸刚度、张紧器刚度、张紧臂长进行优化设计;在以上优化结果基础上,通过减小带弯曲刚度进一步控制SBAD系统振动。
1 梁耦合振动模型

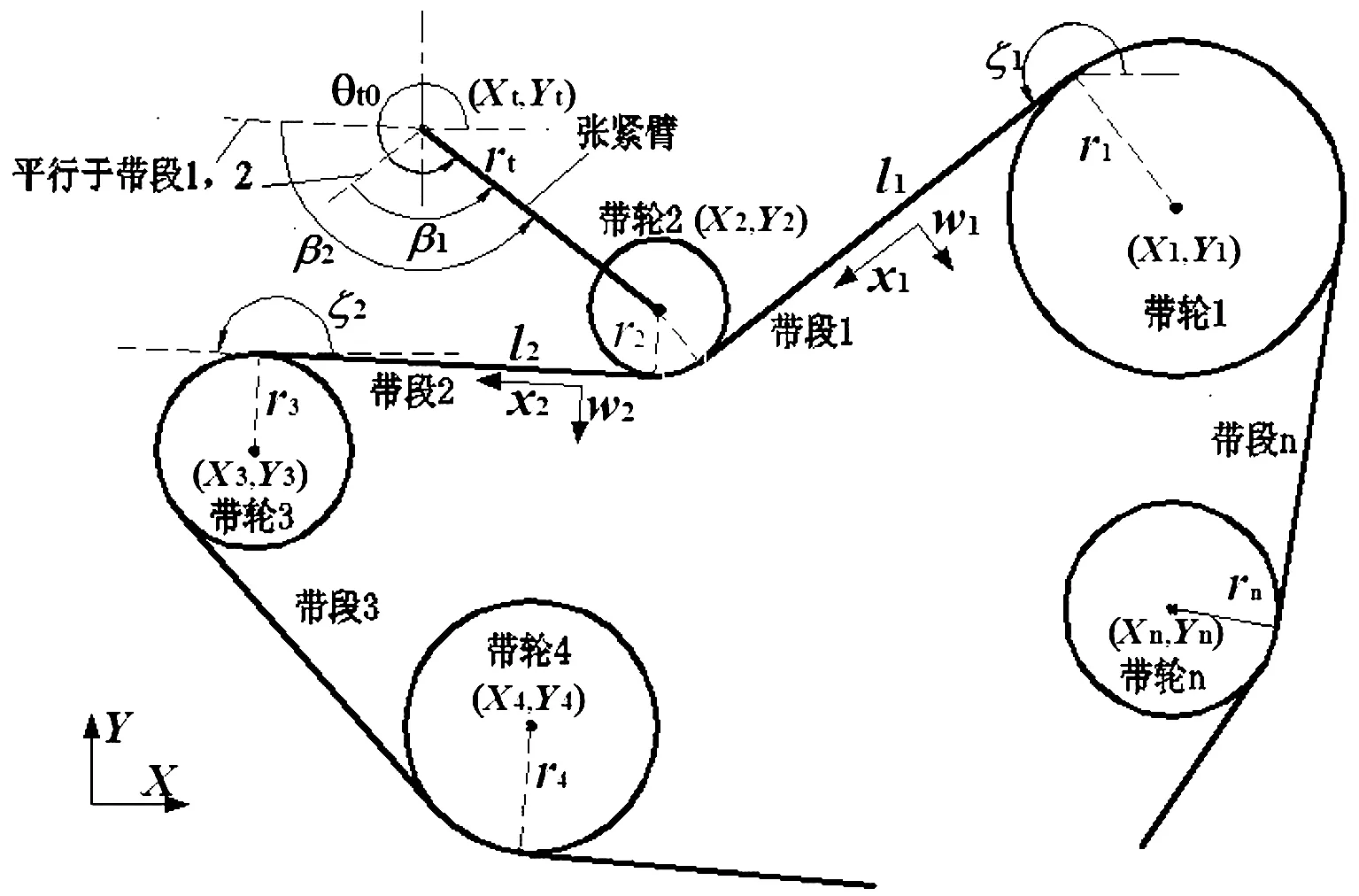
图1 n带轮多楔带附件驱动系统结构示意图Fig.1 Schematic diagram of n pulley SBAD system
假设带的物理特性一致、带与带轮间不打滑、带以准静态方式伸缩。忽略SBAD系统内的阻尼和摩擦,所有运动是相对参考状态(不考虑带弯曲刚度,以弦线模拟带时的稳定状态)的运动。利用Hamilton变分原理和牛顿第二定理建立SBAD系统振动方程;对建立的方程进行无量纲化处理,消去时间项,得到SBAD系统在稳定状态、无负荷作用时的振动方程[1]。其中各带段横向振动方程为:
(1)
式(1)的边界条件为:
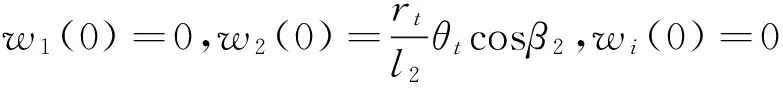
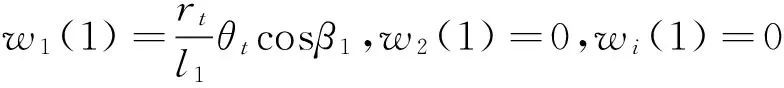
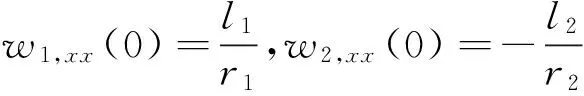
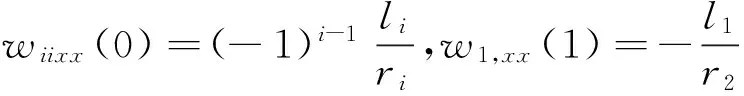
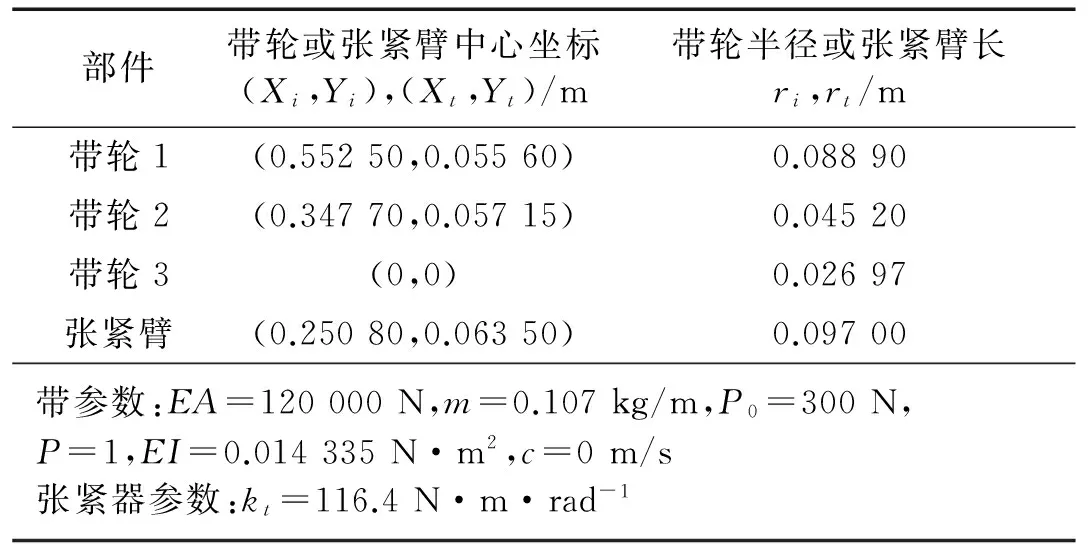
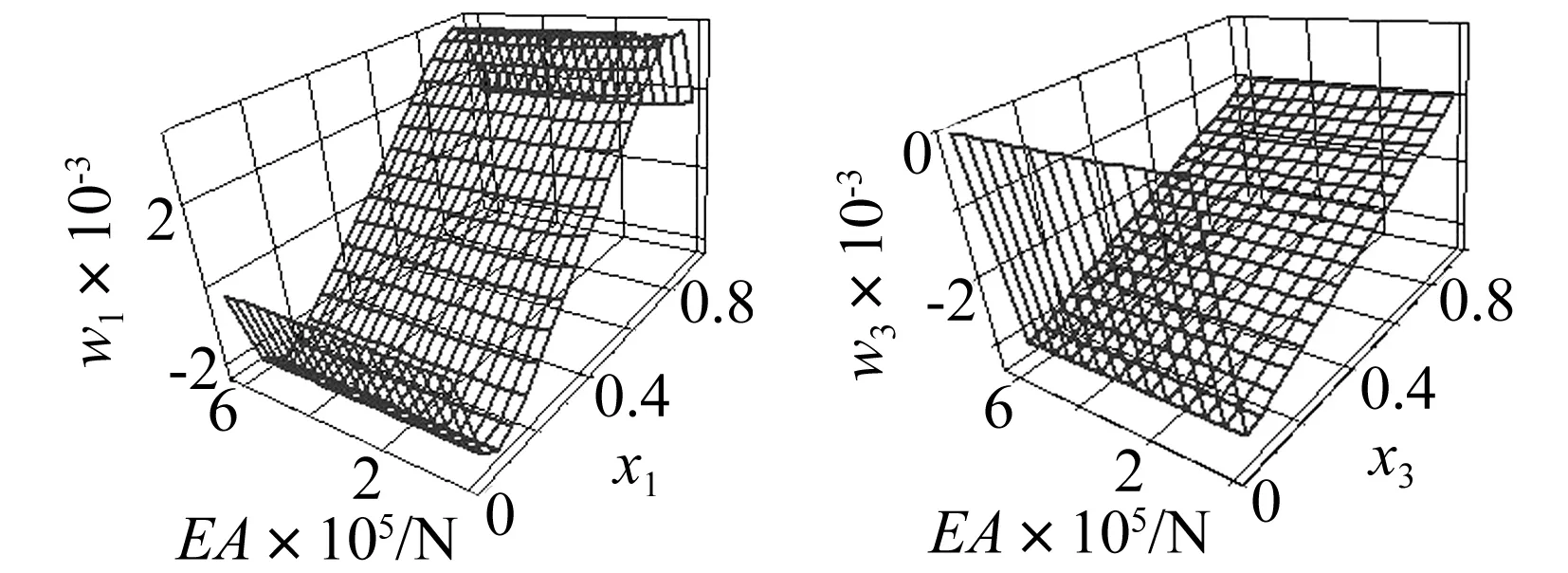
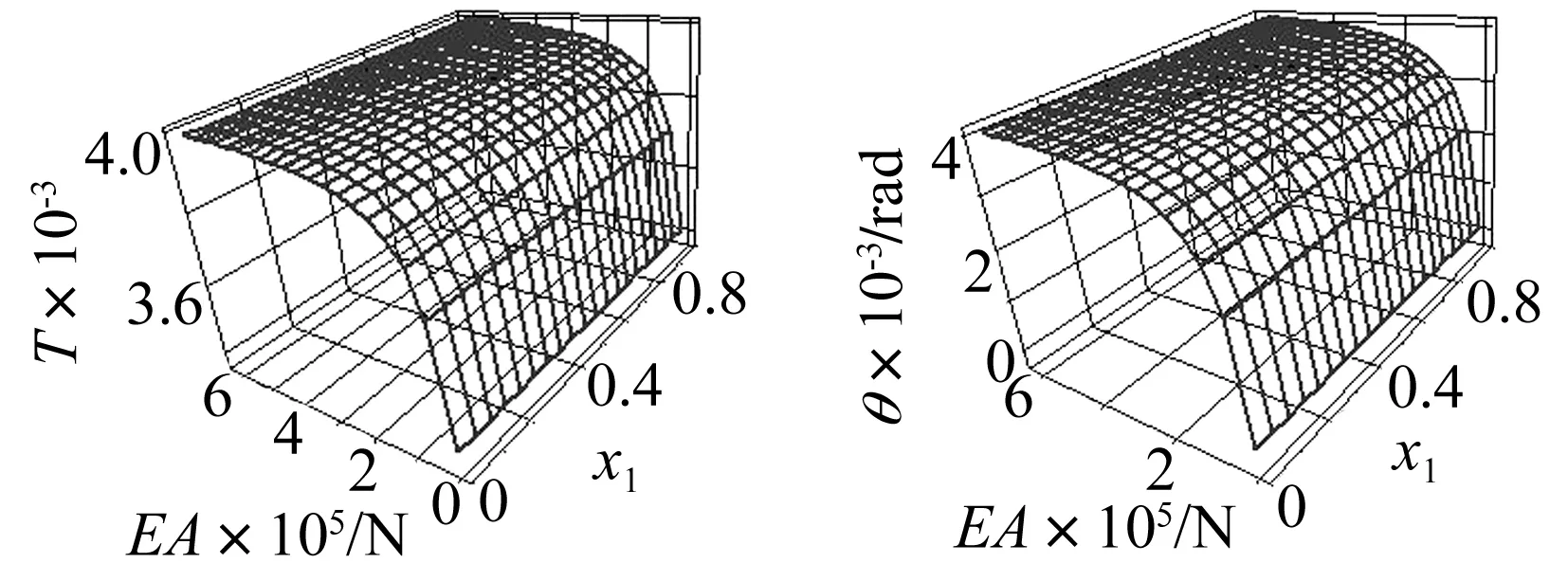
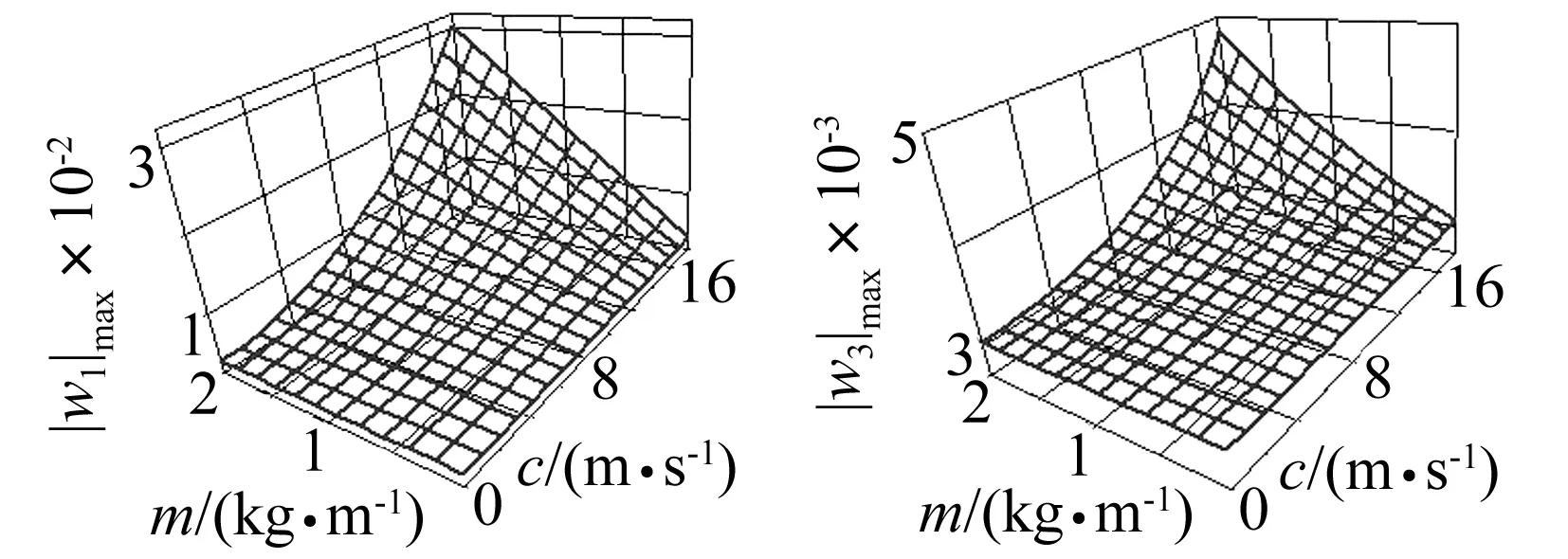
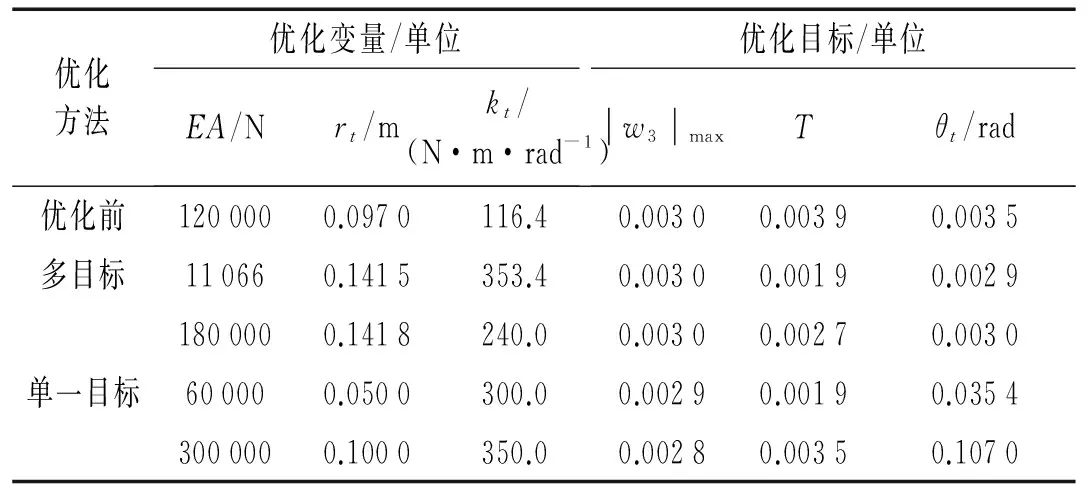
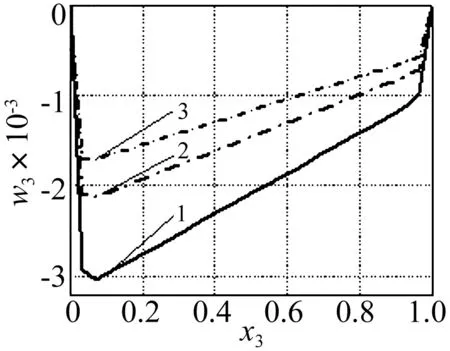
(当1≤i (2) 带轮的振动方程为: (3) 张紧臂的旋转振动方程为: (4) 式(4)中,无量纲量 利用常微分方程转换技术,将方程(1)、方程(3)、方程(4)及边界条件(2)转换为标准的边值问题的常微分方程组来求解[3]。 表1 3带轮SBAD系统参数[3] (a) 带段1横向振动(b) 带段3横向振动 (c) 带动张力(d) 张紧臂摆角图2 带拉伸刚度对SBAD系统振动性能的影响Fig.2InfluenceofbeltlongitudinalstiffnessondynamiccharacteristicsofSBADsystem SBAD系统振动性能包括:带段的横向振动、带动张力波动、张紧臂摆角波动等。这些振动性能影响SBAD系统工作可靠性、寿命,及行驶安全性等,应控制。 为有效传递动力,SBAD系统采用多楔带。多楔带由橡胶、聚酯线绳和玻璃纤维等材料制成。材料成份决定了多楔带性能参数(带拉伸刚度、弯曲刚度和带线密度)的大小,而多楔带性能参数的大小影响SBAD系统振动性能[1-3]。 图2~图4显示了,带参数对表1所示的3带轮SBAD系统振动性能影响的仿真结果。 由图2可知,带段横向振动幅值随EA的增加略微减小,且变化不明显;带动张力、张紧臂摆角随EA的增加而增大。由图3可知,随着EI的增加,带段横向振动幅值、带动张力、张紧臂摆角均增加。EA、EI对带段横向振动幅值的影响与文献[3]研究结果相同。 (a) 带段1横向振动(b) 带段3横向振动 (c) 带动张力(d) 张紧臂摆角图3 带弯曲刚度对SBAD系统振动性能的影响Fig.3InfluenceofbeltbendingstiffnessondynamiccharacteristicsofSBADsystem (a) 带段1横向振动(b) 带段3横向振动 (c) 带动张力(d) 张紧臂摆角图4 带线密度对SBAD系统振动性能的影响Fig.4InfluenceofbeltlineardensityondynamiccharacteristicsofSBADsystem 3.1优化模型 SBAD系统布置时,各带轮的位置和几何尺寸受到整车尺寸、发动机结构尺寸、发动机布置、负荷大小等的限制,改变较难。 在SBAD系统中,张紧器无需驱动附件,其安装位置、结构尺寸、性能参数等较容易改变,常被选作SBAD系统优化设计的变量,如文献[4-5,7,9]。 以下选择多楔带性能参数、张紧器参数作为设计变量对SBAD系统进行优化设计。 带段的横向振动是SBAD系统噪声的主要来源,尤其是主动轮紧边带段的横向振动[10]。控制带段横向振动是SBAD系统设计重点考虑的因素之一。另外,带动张力波动幅值过大会增加带轮轴承负载、加快皮带的磨损,降低轴承、多楔带寿命。张紧臂摆角波动幅值过大会使张紧器弹簧提前失效[7]。为此,选择降低带段横向振动幅值和带动张力、减小张紧臂摆角作为SBAD系统振动性能设计的目标。即,优化设计目标可以表达为: (5) 式中,a1、a2、a3为系数。 令a1=1、a2=1、a3=1,式(5)简化为 (6) 式(6)为多目标优化,可以控制带段最大横向振动幅值、带动张力和张紧臂摆角。 令a1=1、a2=0、a3=0,式(5)简化为 (7) 式(7)为单一目标优化,可以控制带段最大横向振动幅值。 由于EI、m的变化对带段横向振动幅值、带动张力和张紧臂摆角的影响趋势相同,故只选择EA、rt、kt为设计变量,则优化模型的约束条件为 (8) 式(8)中,上标“L”、“U”分别为优化变量取值的下界和上界。 3.2优化结果分析 选用Matlab软件对表1所示的3带轮SBAD系统进行优化设计。考虑张紧器的行程和补偿率,及实际多楔带EA值的可取范围,定义变量的约束条件为 (9) 由文献[2]有多楔带弯曲刚度的取值范围大约为(0.006 9≤EI≤0.530 7)(N·m2),在此范围内减小EI,可进一步控制SBAD系统振动。 表2 优化结果 图5 优化前、后带段3横向振动Fig.5 Belttransverse deflections before and after optimization (1) 带参数对SBAD系统振动性能有影响。随着EA的增加,带段横向振动幅值减小,带动张力、张紧臂摆角增大;EI增加,带段横向振动幅值、带动张力、张紧臂摆角增加;m对带段横向振动的影响是通过带轴向运动速度c来体现的;c固定,带段最大横向振动幅值、带动张力、张紧臂摆角均随着m的增加而增大;随着c的增大,m对系统振动性能的影响增大。 (3) 在以上优化基础上,进一步减小带弯曲刚度值,可进一步降低系统振动。 [1] Beikmann R S, Perkins N C, Ulsoy A G. Design and analysis of automotive serpentine belt drive systems for steady state performance [J]. Journal of Mechanical Design,1997,119(3): 162-168. [2] Zhang L, Zu J W.Modal analysis of serpentine belt drive systems [J]. Journal of Sound and Vibration,1999,222(2): 259-279. [3] Kong L, Parker R G. Equilibrium and belt-pulley vibration coupling in serpentine belt drives [J]. Journal of Applied Mechanics, 2003, 70(5): 739-750. [4] 劳耀新,侯之超,吕振华. 发动机前端附件带传动系统频率灵敏度分析[J]. 汽车工程,2006,28(5):477-486. LAO Yao-xin, HOU Zhi-chao, LÜ Zhen-hua. Frequency sensitivity analysis on belt drive system for front end accessories of engine [J]. Chinese Automotive Engineering, 2006, 28(5): 477-486. [5] Hou Zhi-chao, Lao Yao-xin, Lu Qiu-hai. Sensitivity analysis and parameter optimization for vibration reduction of undamped multi-ribbed belt drive systems[J]. Journal of Sound and Vibration,2008(317):591-607. [6] 张智,上官文斌,许秋海. 多楔带传动系统从动轮-带滑移率的实测与优化控制[J]. 振动工程学报,2010,23(6):616-619. ZHANG Zhi, SHANGGUAN Wen-bin, XU Qiu-hai. Measurement and optimization control of slip rate between driven pulley and belt in serpentine belt drive system [J]. Journal of Vibration Engineering, 2010, 23(6): 616-619. [7] 王象武,侯之超. 基于转动振动控制的发动机前端附件带传动系统优化[J]. 内燃机学报,2011,29(5):475-479. WANG Xiang-wu, HOU Zhi-chao. Optimization on engine front end accessory belt drive based on rotational vibration control [J]. Transactions of CSICE,2011,29(5):475-479. [8] 张少飞,上官文斌,曾祥坤. 具有单向离合器的多楔带附件驱动系统旋转振动建模及参数优化设计[J]. 振动与冲击,2012, 31(13): 163-168. ZHANG Shao-fei, SHANGGUAN Wen-bin, ZENG Xiang-kun. Rotational vibration modeling and optimization design of serpentine belt accessory drive system with one-way clutch [J]. Journal of Vibration and Shock, 2012, 31(13): 163-168. [9] 上官文斌,王红云,张智. 多楔带传动系统振动建模及带段横向振动控制的研究[J]. 振动工程学报,2009,3(22):250-255. SHANGGUAN Wen-bin, WANG Hong-yun, ZHANG Zhi. Dynamic modeling of serpentine belt drive systems and the transverse vibration control of the belt [J]. Journal of Vibration Engineering, 2009, 3(22): 250-255. [10] 刘元冬,王文林,罗明军. 基于Adams发动机前端附件带传动的动态特性研究[J]. 机械传动,2013,37(6):28-32. LIU Yuan-dong, WANG Wen-lin, LUO Ming-jun. Research on dynamic characteristic of belt drive system of engine front end accessory based on ADAMS [J]. Journal of Mechanical Transmission, 2013, 37(6): 28-32. Optimization for a serpentine belt accessory drive system based on vibration control WANG Hong-yun1, ZENG Xiang-kun1, XIANG Ying2, ZHAO Ji-yong3 (1. School of Automotive Engineering, Guangdong Polytechnic Normal University, Guangzhou 510665, China;2. School of Electronic Information Engineering, Guangdong Polytechnic Normal University, Guangzhou 510665, China;3. Shandong Meichen Science and Technology CO., Ltd, Zhucheng 262200, China) The rotary-transverse vibration coupled model for a serpentine belt accessory drive (SBAD) system was established considering belt bending stiffness. A three-pulley SBAD system was taken as an example. The effects of longitudinal stiffness, bending stiffness and belt linear density on the dynamic characteristics of the system, such as, the transverse vibration, the tension fluctuation and the rotation angle of the tensioner’s arm were investigated. One optimization strategy was proposed and implemented to control the system’s vibration. In the optimization strategy, belt longitudinal stiffness, tensioner stiffness and tensioner’s arm length were taken as design variables, while the transverse deflections of belt, the fluctuation of belt tension and the rotation angle of the tensioner’s arm were used to define the objective function. On the basis of the above optimization results, the belt bending stiffness was reduced to further improve the dynamic characteristics of the system. serpentine belt accessory drive system; rotary-transverse vibration coupled model; optimization design; vibration control 10.13465/j.cnki.jvs.2016.13.032 国家自然科学基金资助项目(51305085) 2015-03-09修改稿收到日期:2015-05-21 王红云 女,博士,讲师,1971年6月生 TH132.3;TK423.42 A
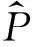
2 带参数对SBAD系统振动性能影响


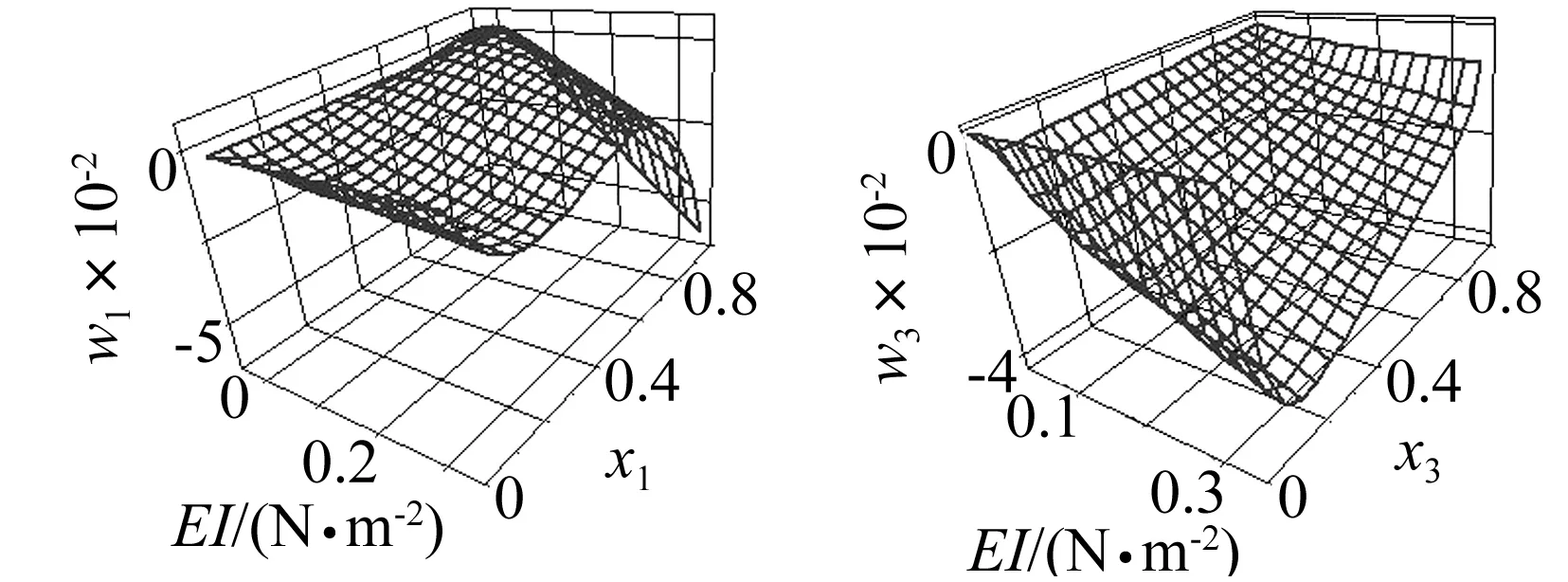

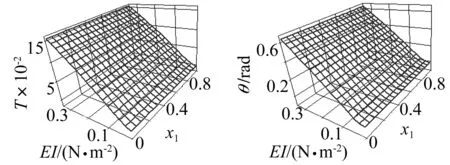




3 优化模型与仿真结果分析
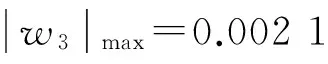
4 结 论