静立人群与板联合系统动力学特性研究

韩慧璇， 周　叮， 刘伟庆

(南京工业大学 土木工程学院，南京　211816)

静立人群与板联合系统动力学特性研究

韩慧璇， 周叮， 刘伟庆

(南京工业大学 土木工程学院，南京211816)

采用能量法研究静立人群与板联合系统的动力学特性。使用具有分布质量、阻尼和刚度的非均质弹性直杆模拟静立人体，利用第一类切比雪夫多项式构造板的试函数，结合拉格朗日方程建立人-板联合系统振动微分方程，分析了人-板系统的动力学特征，详细研究了人的位置以及人板质量比对人-板系统动力特性的影响。分析表明：弹性人体模型比附加质量模型更科学合理，人群位于板动力变形较大处时对系统动力特性的影响尤为显著。

人-板联合系统；人体模型；振动微分方程；动力特性

随着城市建设的迅猛发展和轻质高强建筑材料的应用，涌现了大批造型独特、结构新颖的大跨公用建筑诸如大型车站、体育场馆等。这些大跨结构大都具有自振频率低和人群密度大等特点，结构很容易被驻留人群的活动所激振，使得人群的舒适度降低[1]，严重的甚至会导致结构损坏和人群拥挤践踏，这类结构与人的相互作用问题引起了人们的广泛关注。

人与结构相互作用问题的研究包括两个方面[2]：结构动力学和人体生物动力学。目前，国内外学者对其研究主要包括三类：① 人的运动引起的激振力；② 人的驻留导致结构动力特性的改变；③ 静止和运动人体模型的建立。早期研究通常将驻留人群荷载看作静载，考虑为结构上的附加质量，认为人群会降低结构的频率，而不改变结构的阻尼。Lenzing[3]通过对木板的动力测试发现，当人驻留在板上时，系统的自然频率没有减小，反而略有增加，且结构的阻尼显著增加。Ellis等[4]测试Twickenham露天体育馆看台发现，人群驻留时，系统的动力特性增加了一个主要模态。使用传统的附加质量模型不能解释这些现象，需要将人体表征为附加于结构上的一个动力学系统。Matsumoto等[5-6]等研究并建立了不同的人体动力简化模型，通过测试60位站立人体的基频和阻尼比来验证其人体模型。Sachse[7]将结构和人群分别简化为单自由度体系，建立了有阻尼的人群-结构相互作用模型，但这种简化方法没有考虑人群与结构二阶以上振型的相互作用。孙利民等[8]对人行桥人致竖向和侧向振动方面进行研究，建立了同步调自激侧向力模型，将同步调步行力等效为大小与振幅相关的附加刚度和阻尼。Zhou[9]将人群简化成具有分布质量的单自由度质量-弹簧系统，忽略人体和结构的阻尼，研究了人群驻留对板动力特性的影响。

目前，对于人与结构相互作用的研究主要是人-梁系统[10]，而关于人-板系统的研究相对较少，且大多是只考虑楼板的一阶模态并忽略人、板阻尼的影响[11]。本文利用生物力学知识，采用具有分布质量、刚度和阻尼的人体弹性模型。用切比雪夫多项式构造板的试函数，与能量法相结合，利用拉格朗日方程建立了人-板相互作用动力学模型，分析了人-板的动力学特征。

1　矩形薄板的振动分析

1.1矩形薄板的试函数

为了数学公式的方便简洁，引入两个无量纲参数：

α=2x/a，β=2y/b

(1)

式中，a和b分别为矩形板的长和宽，矩形板在竖直方向上的位移w为[12]：

(2)

式中，Wkl(α,β)为薄板的试函数，Akl(t)为其幅值坐标。

分别利用第一类切比雪夫多项式和简单多项式构造矩形薄板的试函数：

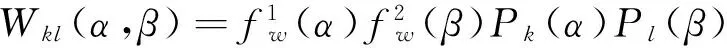
(3)

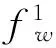
Ps(χ)=cos[(s-1)arccos(χ)]，s=1,2,3,…

(4)

表1　矩形薄板不同边界条件下的边界函数分量

注：F：自由边； S：简支边； C：固支边

使用切比雪夫构造试函数有两个显著优势：① 切比雪夫多项式可用统一的三角余弦函数表示，便于公式的推导和程序的编制；②Ps(χ)(s=1,2,3,…)在[-1,1]区间内是完备的正交级数，在所有多项式级数中，切比雪夫多项式的数值稳定和收敛性最好，可保证计算的鲁棒性和高精度。图1给出了前六项切比雪夫多项式的曲线图。

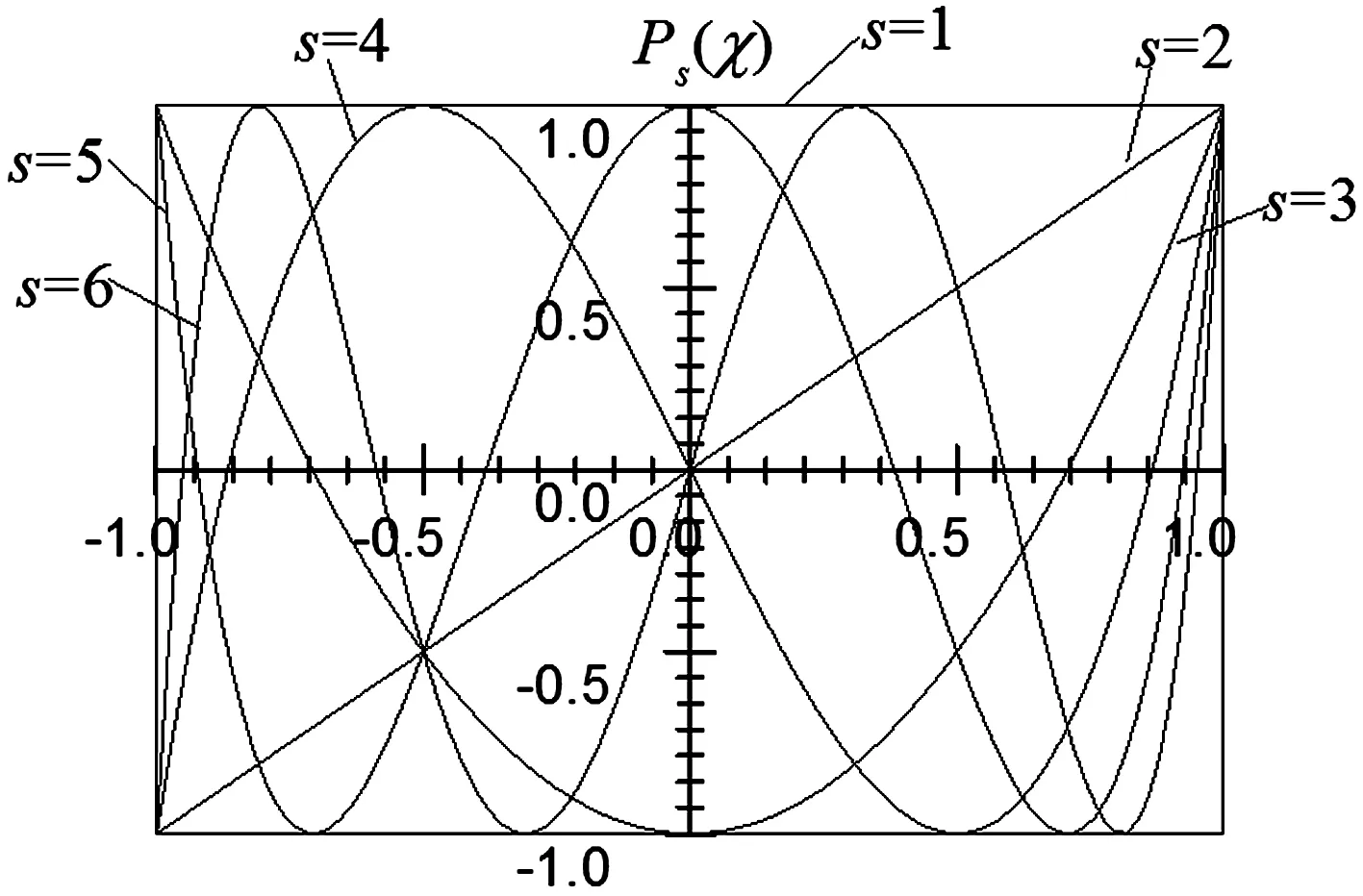
图1　前六项切比雪夫多项式Fig. 1 The first six Chebyshev polynomials

1.2矩形薄板的自振频率和振型

板作自由振动时，令：

Akl(t)=Bklsin(ωt+φ)

(5)

式中，Bkl(k,l=1,2,3,…)是待定系数，ω为结构的固有频率，φ为相位角。

板的最大势能和最大动能分别为：

(6)

(7)

能量函数定义为：

=Umax-Tmax

(8)

对式(2)做截断，由瑞利-李兹法得：

∂/∂Bkl=0,

(k=1,2,3,…,p;l=1,2,3,…,q)

(9)

将式(2)～(8)代入式(9)中，得频率方程：

(k=1,2,3,…,p;l=1,2,3…,q)

(10)

式中：

λ2=ρhω2a4/(16D),γ=a/b,

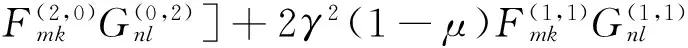
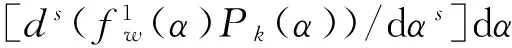
(11)

式中，I=p×q。

取长宽比γ=1，泊松比μ=0.2。分别使用两种多项式构造四边固支矩形板的试函数，无量纲固有频率的收敛性见表2。由表2可知，当试函数项数小于等于10时，切比雪夫多项式与简单多项式的计算结果相同；当试函数项数大于等于12时，简单多项式作试函数得到的矩阵方程呈病态，无法给出正确结果，而切比雪夫多项式的计算结果不单精确而且稳定，表明在求解高阶模态频率时，切比雪夫多项式的鲁棒性显著优于简单多项式。

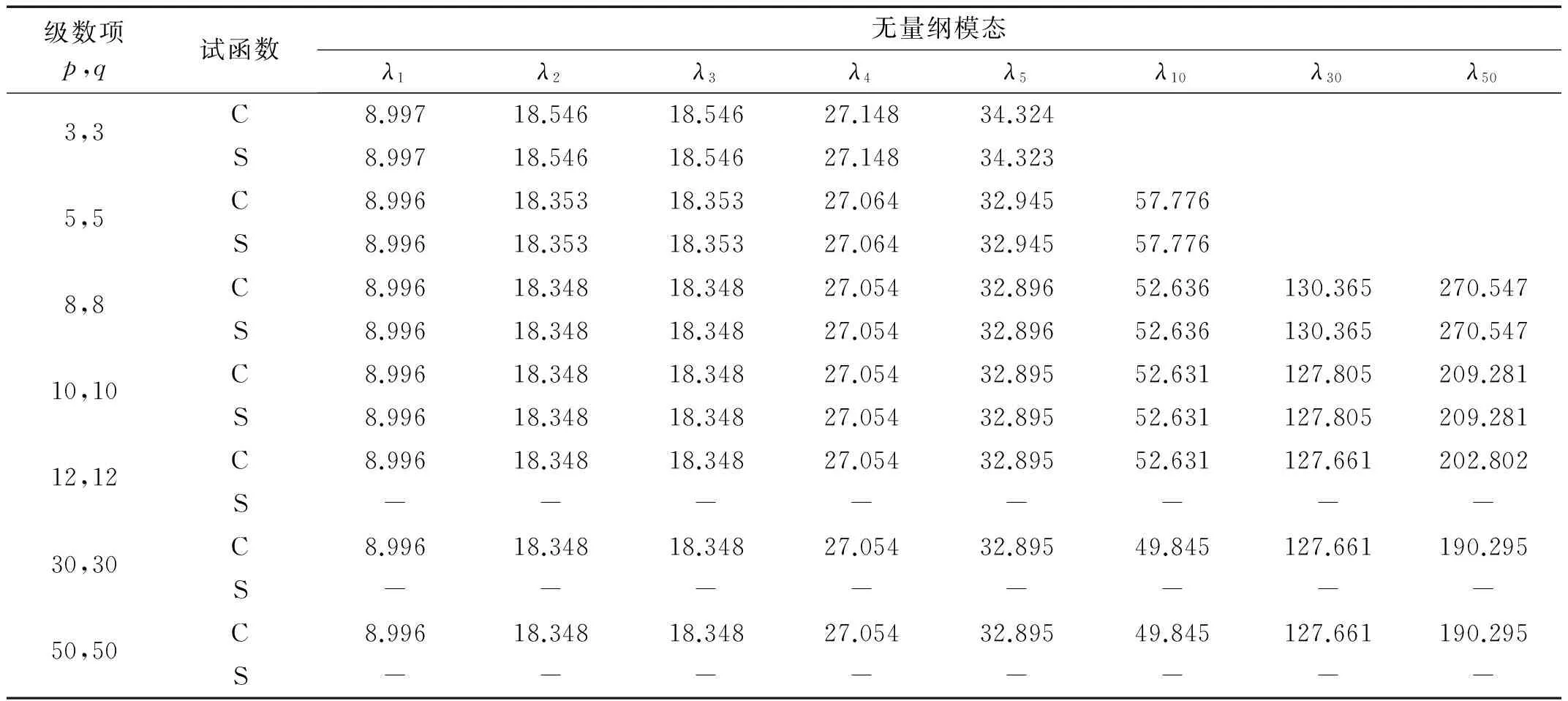
表2　使用切比雪夫多项式和简单多项式作试函数的四边固支矩形板频率系数收敛性的比较

注：C表示切比雪夫多项式；S表示简单多项式。

2　人体的模态参数

为研究人-矩形板联合体系的动力特性，现根据生物力学知识,定义人体的模态参数、频率和阻尼比的参数值。

2.1人体的模态函数φH(x)的确定

生物力学研究常用分段的连续弹性直杆近似模拟人体，本文采用的是简单的两段弹性直杆模型[13]，设每段直杆的质量均布，沿竖直方向的刚度也均布，如图2所示。

每段直杆的轴向振动微分方程为

(12)

式中，mi和ki为每段杆件的单位长度的质量和轴向刚度。

令式(12)的解为：

ui(x,t)=Zsin(ωHt+φi)φi(x),i=1,2

(13)

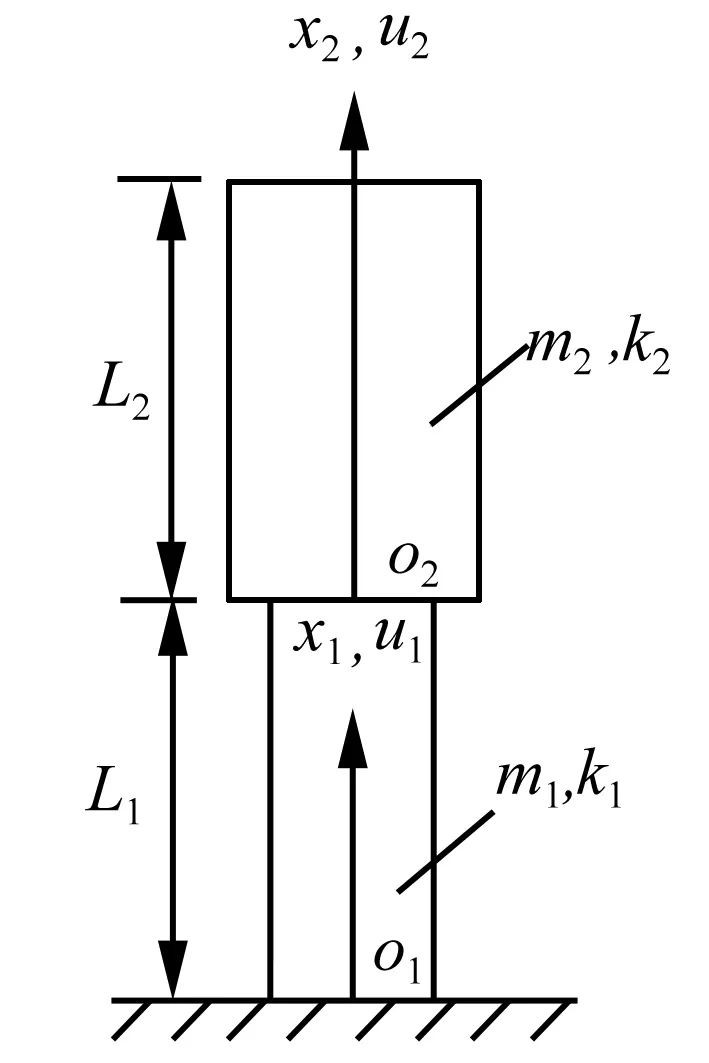
图2　人体竖直方向的振动模型Fig.2 The model of a body vibrating in vertical direction

式中，ωH为人体的振动频率，φi为相位角，φi(x)为模态函数，Z为振幅。考虑人体脚部固定，头顶自由，并利用上下两段直杆连接处变形和受力的协调条件，得人体的振型函数为：

φ1(x1)=Dsinb1x10≤x1≤L1

φ2(x2)=D(sinb1L1cosb2x2+

(14)

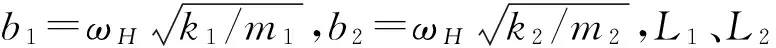
从而得到人体垂直振动频率的超越方程为：

(15)

进而得到人体总质量MT、人体与结构联合质量MHS、人体模态质量MH的表达式：

(16a)

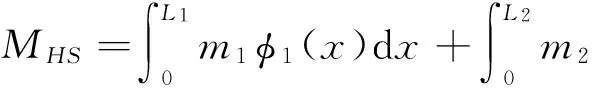
(16b)

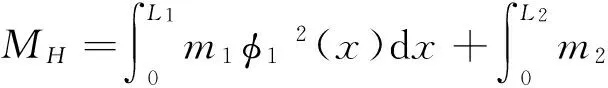
(16c)

生物研究水平的局限性使人体均布质量和刚度很难精确获取，因此根据已有研究[13]，取L1=L2，m2=2m1，k2=2k1，得广义人体的等效质量为：MHS=0.765 9MT，MH=0.666 7MT。

2.2人体的平均频率ωH和阻尼比ξH的确定

人体在垂直方向的固有振动基频在4 Hz～6 Hz，阻尼比在40%～50%。根据Wei等[6]对60个站立人体的基频和阻尼比的测量的数学平均，得人体的基频ωH为5.5 Hz，阻尼比ξH为0.42。

3　人-板联合系统动力学模型

人-矩形板联合动力模型如图3所示。假设有J人静立在矩形板上，每个人距板中心的坐标位置为(αj,βj)(j=1,2,…,J)处。m(z)、k(z)、c(z)分别为广义人体模型的平均分布质量、分布刚度、分布阻尼，坐标z表示人体部位到脚部的距离，L为人体高度，c(α，β)为矩形板的阻尼分布。

仅考虑人体的基阶模态，第j个人体的竖向位移wHj(α,β,t)为：

wHj(α,β,t)=w(αj,βj,t)+wRj(z,t)=

w(αj,βj,t)+wHRj(t)φH(z)=

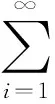
(17)

式中，wRj(z,t)为第j人相对于矩形板的竖向位移，w(αj,βj,t)为(αj,βj)处矩形板的位移，φH(z)为广义人体的基阶振型函数。

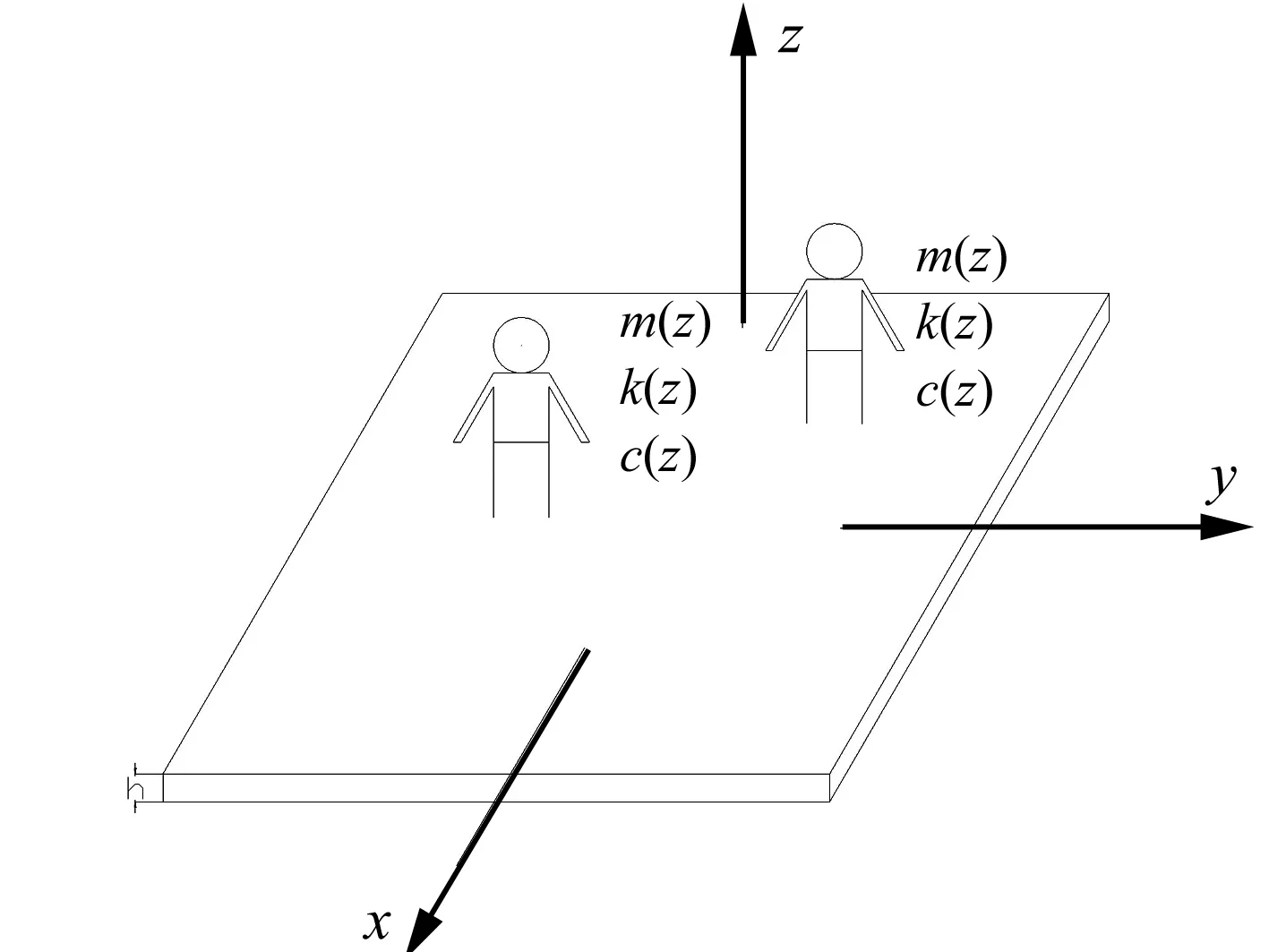
图3　人-矩形板联合系统模型Fig.3 The model of human-plate coupled system

人-矩形薄板联合系统的势能为：

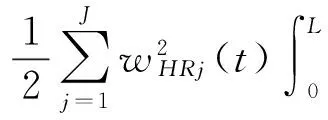
(18a)

人-矩形薄板联合系统的动能为：

人-矩形薄板联合系统的阻尼耗能为：

(18c)

拉格朗日方程为：

(i=1,2,…,I)

(j=1,2,…,J)

(19)

将式(18a)～(18c)代入式(19)中，得到人-板联合系统的I+J阶自由振动微分方程：

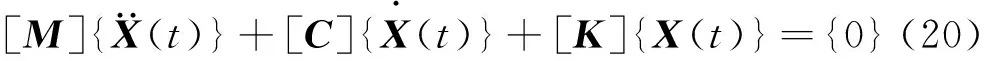
式中:{X(t)}=[Y1(t),Y2(t),…,YI(t),wHR1,wHR2,…,wHRJ]T

引入如下参数：

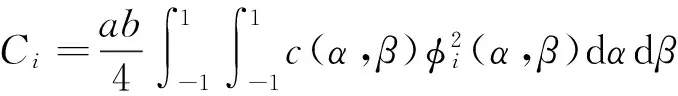
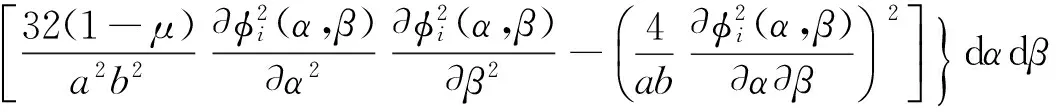
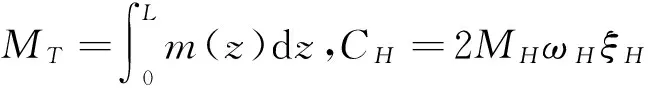
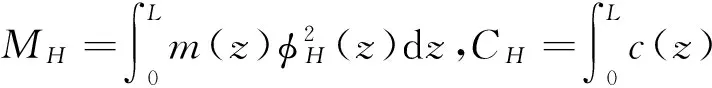
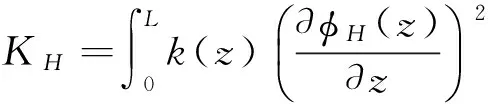
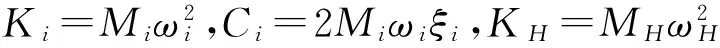
考虑板模态的正交性，则式(20)中的广义质量矩阵、阻尼矩阵和刚度矩阵分别为：

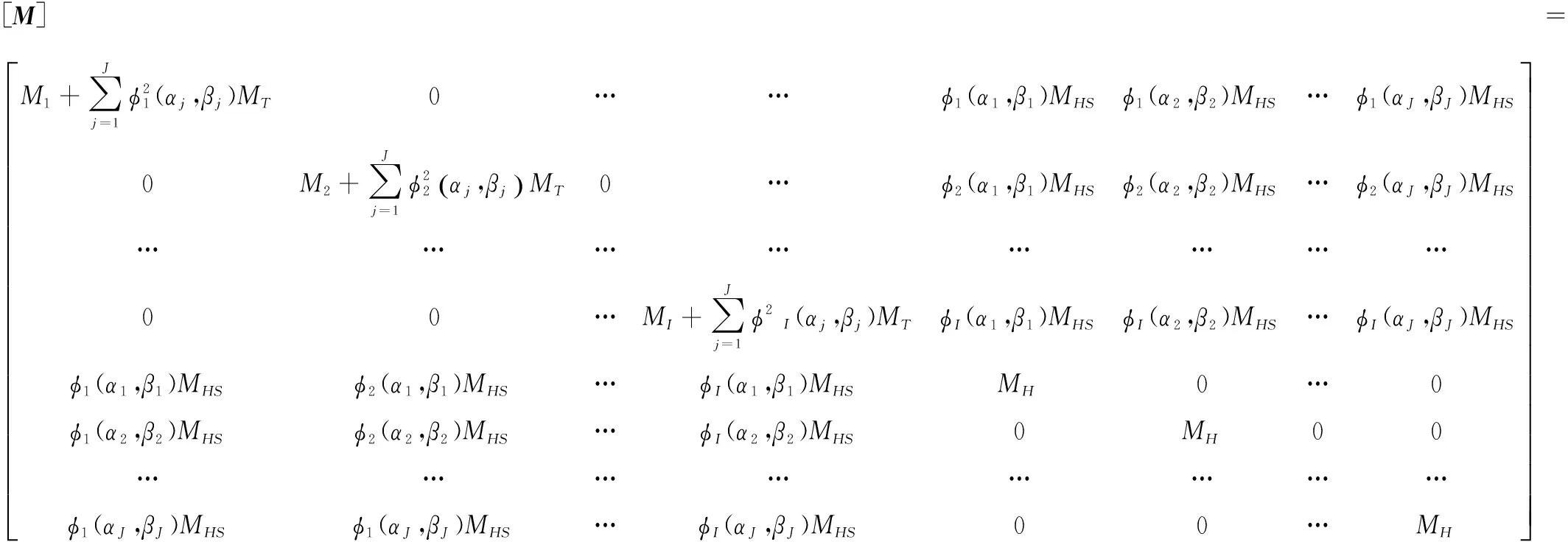
复模态分析法分析该振动方程，求出联合系统前I+J阶的复特征根λr和复特征向量{ψ}r。联合系统的前I+J阶频率fr和阻尼比ξr分别为:

r=1,2,…,I+J

(21)

4　收敛性及精度验证

为验证本文所建立的人-板联合系统模型的精度和准确性，对静立人群与四边固支混凝土方板联合系统的前四阶模态频率和阻尼比的收敛性进行数值计算，计算参数为：板的平面尺寸a×b=11 m×11 m，厚度h=0.15 m。混凝土强度等级C30，密度ρ=2 400 kg/m3，泊松比μ=0.2，杨氏模量E=30×109N/ m2。取人体的平均质量MT=70 kg，基阶模态质量46.669 kg，人体与结构联合质量MHS=53.613 kg，平均基频ωH=5.5 Hz，平均阻尼比ξH=0.42[6,14]，下面的研究着重于人体对结构固有频率和阻尼的影响。

表3给出了人与板质量比ν分别为0.1、0.4和1.0时，不同项数切比雪夫多项式下该联合系统前三阶的固有频率和阻尼比。由表3可知，结果随所取多项式项数的增加而迅速收敛。当Ps(χ)取10×10项时，可保证前三阶频率和阻尼比具有5位数的精度，因此后续计算均取10×10项切比雪夫多项式。

为验证本文人-板联合系统模型的正确性，用Sap2000有限元软件数值模拟静立人群与四边固支混凝土方板联合系统的前三阶频率。取人体的间隙为0.5m，人群沿板中心四周对称均匀分布，使用线性连接单元模拟人体的刚度KH，使用带重量的黏滞阻尼器模拟人体的阻尼CH以及人体与结构的耦合质量MHS-MH，结果如表4所示。从表中看出，人-板1阶频率随人板质量比的增加而增大，当人与板质量比为1.0时，1阶频率增大了12.306%； 但2阶和3阶频率均随人数的增加而逐渐减小，且与1阶频率相比，后两阶的变化幅度显著降低，即高阶频率对人数的变化敏感性下降。人-板前3阶频率的理论解与有限元解吻合较好，其最大误差为4.9603%，不超过5%，证明了本文方法的正确性。

表4　有限元和本文结果的比较

5　人对矩形薄板动力特性的影响

对于有人驻留的结构，人体主要对结构的低阶模态有较大影响。本文对上节中的矩形薄板进行人体参数化分析，计算了人-矩形薄板联合系统的前三阶模态频率和阻尼比，并将其与空板的模态频率和阻尼比进行比较，空板的前三阶无阻尼固有频率为：f11=7.395 7 Hz，f12=15.083 9 Hz，f22=22.240 7 Hz。设前三阶结构的阻尼比均为1%。

5.1单人对四边固支方板动力特性的影响

让单个人体的位置从板中心(0，0)变化到板端。图(4a)～(4f)分别给出了单人-固支方板联合系统以板振动为主的前三阶模态频率和阻尼比与所在位置的关系曲线。

由图(4a)～(4f)可知，联合系统的前三阶模态频率和阻尼比与人的位置相关,当人位于板动力变形较小处(板边附近)时，人-板联合系统的模态频率和阻尼比基本等于该空板的前三阶固有频率和阻尼比。随着人向板动力变形最大处(板中心)靠近，系统的第一阶模态频率逐渐减小，当人到达板中心时频率值最小；而第一阶模态阻尼比的变化趋势与第一阶模态频率的变化趋势相反。

对于其他边界条件的矩形薄板，诸如三边自由一边固定的悬臂板也作了计算，可得到与四边固支板同样的结论：人体站立于板动力变形较大处(悬臂板边缘)时的影响显著，限于篇幅，这里不再缀述。

5.2人与板质量比对方板动力特性的影响

由上节的模拟结果可知，当单个人位于四边固支薄板中心附近时，薄板的动力特性变化显著，下面考虑人群沿板的中心四周对称均匀分布，人体的间隙均为0.5 m。图(5a)～(5f)分别给出了不同边界条件下人-板联合系统以板振动为主的前三阶模态频率和阻尼比与人-板质量比的关系曲线，图5同时给出了传统的人体附加质量模型对频率和阻尼比的影响以及悬臂方板的计算结果。

由图(5a)～(5f)可知，使用传统的附加质量人体模型，人数的增加只降低人-固支方板联合系统的前三阶频率，而系统的阻尼比不变，这明显与Lenzing[3]的实验结果不一致。使用本文的人体模型，人-固支方板联合系统前三阶的模态频率和阻尼比均与人数相关。当人群沿板中心(固支板动力变形最大处)四周均匀对称布置时，随着人数的增加，系统第一阶频率逐渐增大，而第二阶频率和第三阶频率逐渐减小，系统前三阶模态的阻尼比均随人数的增加而增大，当人数增加到一定量后，人-板质量比对系统动力特性的影响趋于稳定。对于悬臂板，人群分布越靠近悬臂(悬臂板动力变形最大处)端，对系统动力学特性的影响越大。

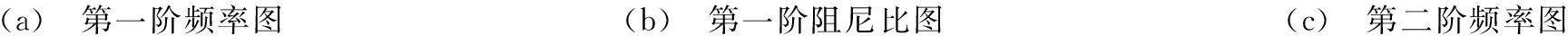
(a) 第一阶频率图(b) 第一阶阻尼比图(c) 第二阶频率图

(d) 第二阶阻尼比图(e) 第三阶频率图(f) 第三阶阻尼比图图4 单人位置变化对人-板联合系统的动力特性的影响Fig.4Thepositioneffectofsinglehumanonthedynamiccharacteristicsofhuman-platesystem

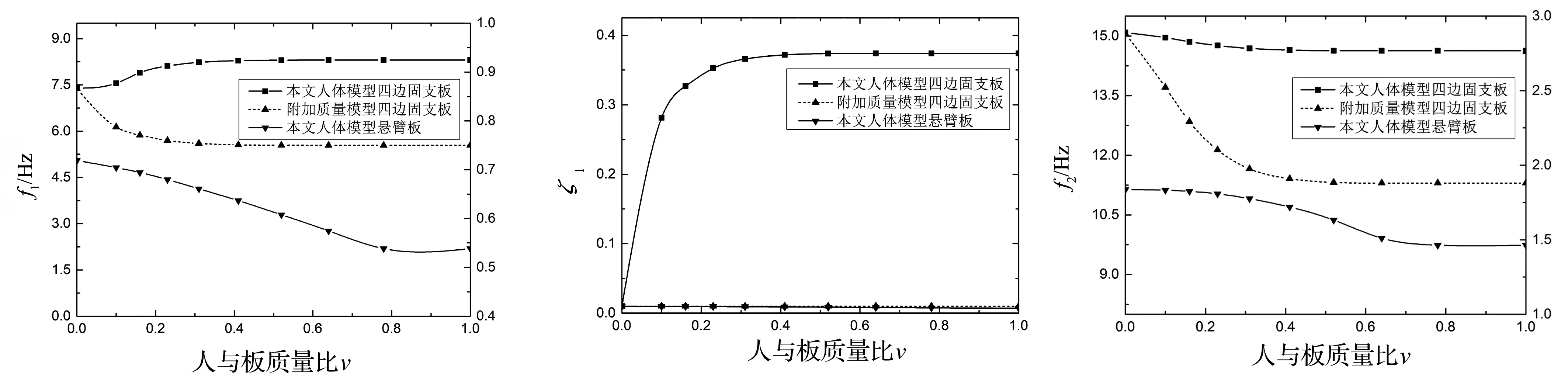
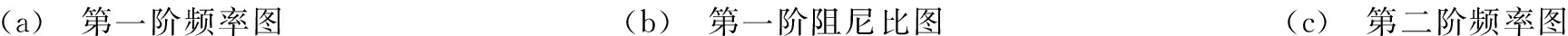
(a) 第一阶频率图(b) 第一阶阻尼比图(c) 第二阶频率图

(d) 第二阶阻尼比图(e) 第三阶频率图(f) 第三阶阻尼比图图5 人与板的质量比变化对人-板联合系统的动力特性的影响Fig.5Theeffectoftheratioofhumantostructureondynamiccharacteristicsofhuman-platesystem

6　结　论

本文采用具有分布质量、阻尼和刚度的非均质弹性直杆的人体模型，建立了人-矩形薄板联合系统的动力学分析模型，研究了人-板联合体系的动力特性，主要结论如下：

(1) 使用切比雪夫多项式构造矩形薄板的试函数优势显著，数值计算的收敛性好、精度高，优良的鲁棒性保证了结构高阶动力学特性的计算有效性。

(2) 将人体作为一个弹性体系附加到结构上比传统的将人体考虑为静态的附加质量更为科学合理，减小了由于人体模型建立不够准确带来的误差。

(3) 人群对板振动特性的影响与人-板质量比呈正比，人群位置靠近板动力变形较大处时对系统动力学特性的影响尤为显著。

[1] 折雄雄，陈隽.大跨度楼盖振动舒适度研究综述 [J].结构工程师，2009，25(6):144-149.

SHE Xiong-xiong, CHEN Jun. A review of vibration serviceability for long-span floors [J]. Structural Engineers, 2009，25(6) : 144-149.

[2] Ji T. Understanding the interactions between people and structures [J]. The Structural Engineers,2003,81(14):12-13.[3] Lenzing H. Durchmenschen induzierte schwingungen [D]. Germany: Universität Hannover, 1988.

[4] Ellis B R, Ji T. Human-structure interaction in vertical vibrations [J]. Proceeding of the ICE: Structures and Buildings, 1997, 122(1): 1-9.

[5] Matsumoto Y, Griffin M J. Dynamic response of the standing human body exposed to vertical vibration: influence of posture and vibration magnitude [J]. Journal of Sound and Vibration, 1998, 212(1): 85-107.

[6] Wei L, Griffin M J. Mathematical models for the apparent mass of the seated human body exposed to vertical vibration [J]. Journal of Sound and Vibration, 1998, 212(5): 855-874.

[7] Sachse R. The influence of human occupants on the dynamic properties of slender structures PHD [D]. UK: The University of Sheffield, 2002.

[8] 袁旭斌.人行桥人致振动特性研究 [D].上海:同济大学，2006.

[9] Zhou Ding, Ji Tian-jian. Free vibration of rectangular plates with continuously distributed spring-mass [J]. International Journal of Solids and Structures,2006,43(21):6502-6520.

[10] 王海，周叮，王曙光.人-梁相互作用动力学模型研究[J].工程力学，2010，27(5):14-20．

WANG Hai, ZHOU Ding, WANG Shu-guang. Modeling of the dynamic interaction of human occupants and beam [J]. Engineering Mechanics, 2010, 27(5): 14-20.

[11] 何卫, 谢伟平, 刘隆.人-板耦合系统动力特性研究[J]. 工程力学, 2013, 30(1): 295-300.

HE Wei, XIE Wei-ping, LIU Long. Study on dynamic characteristics of human-floor interaction system [J]. Engineering Mechanics, 2013, 30(1): 295-300.

[12] Zhou D. Three-dimensional vibration analysis of structural elements using Chebyshev-Ritz method [M]. Science Press, 2007.

[13] Ji T. A continuous model for the vertical vibration of the human body in a standing position [C]// United Kingdom Informal Group Meeting on Human Response to Vibration. Bedford, UK: 1995.18-29.

[14] Sachse R, Pavic A, Reynolds P. Human-structure interaction in civil engineering dynamics: A literature review [J]. The Shock and Vibration Digest,2003,35(1):3-18.

Dynamic characteristics of a standing crowd-plate coupled system

HAN Hui-xuan, ZHOU Ding, LIU Wei-qing

(College of Civil Engineering, Nanjing Tech University, Nanjing 211816, China)

The dynamic characteristics of a standing crowd-plate system were studied adopting the energy method.The coupled model of the crowd-plate system was developed taking the standing human body as an elastic non-uniform column with distributed mass, damping and stiffness. The first kind of Chebyshev polynomials was applied to construct the trial functions for the plate. The governing vibration differential equations of the crowd-plate coupled system were derived using Lagrange equation. The effects of mass ratio of crowd to plate and position of human occupants on the dynamic properties of the crowd-plate system were investigated in detail. The results showed that regarding a crowd as an elastic model added to the plate is more scientific and rational compared with an added mass model; the influence of the crowd on the dynamic characteristics of the crowd-plate coupled system is much more significant when the crowd locates at the positions of the plate with larger dynamic deformations.

crowd-plate coupled system; human-body model; dynamic differential equations;f dynamic characteristic

10.13465/j.cnki.jvs.2016.13.030

国家自然科学基金(11372127)；江苏省属高校自然科学研究重大项目(12KJA580002)；江苏省研究生科研目创新计划项(KYZZ15_0232)资助

2015-04-27修改稿收到日期：2015-07-22

韩慧璇 女，博士生，1991年2月生

周叮 男，博士，博士生导师，1957年5月生

E-mail:dingzhou57@yahoo.com

TU311.3

A