时滞脉冲切换系统的实用稳定性-带Razumikhin条件的Lyapunov函数方法

李少娥, 冯伟贞

(1.华南师范大学数学科学学院,广东广州510631;2.桂华中学,广东佛山528200)

时滞脉冲切换系统的实用稳定性-带Razumikhin条件的Lyapunov函数方法

李少娥1,2, 冯伟贞1

(1.华南师范大学数学科学学院,广东广州510631;2.桂华中学,广东佛山528200)

用带Razumikhin条件的Lyapunov函数方法研究了一般形式的时滞脉冲切换系统的实用稳定性,得到了时滞脉冲切换系统实用稳定、一致实用稳定的充分条件.最后,给出了具体的例子及其数值模拟.

时滞脉冲切换系统;实用稳定;Razumikhin条件;Lyapunov函数方法

§1 引 言

近年来,时滞脉冲切换系统得到了学者的广泛重视,见文献[1-3].这些文献主要研究系统的Lyapunov稳定性.由于Lyapunov稳定性在现实生活中应用的局限性,切塔耶夫等人提出了实用稳定性的概念.

实用稳定性研究的主要问题是初始扰动在一个可行范围内发生时,系统的实际运动状态误差是否也在一个容许的误差发围内.目前,有文献[4-8]对微分系统的实用稳定性进行了研究.其中,文[4-6]涉及各种方程组(包括常微分、脉冲微分与泛函微分等方程组)的实用稳定性.文[7]用Caychy矩阵的方法研究了脉冲切换系统的实用稳定性.文[8]用微分不等式与Lyapunov函数相结合的方法给出了线性时滞脉冲切换系统实用稳定性的充分条件.

Razumikhin技巧是研究带时滞的微分方程稳定性的一种非常有效的方法.文[9-10]借助Razumikhin条件和Lyapunov函数方法,得到了时滞脉冲微分方程指数渐近稳定的若干定理.但鲜有文献用带Razumikhin条件的Lyapunov函数方法对时滞脉冲切换系统的实用稳定性进行研究.

本文通过建立多Lyapunov函数,将文[9-10]中的Razumikhin技巧迁移至时滞脉冲切换系统的实用稳定性研究中.其中,通过用分段处理的方法,解决了因脉冲和切换控制带来的不连续的问题以及多Lyapunov函数间的相容问题.在此基础上,本文给出了两个实用稳定性的定理.其中,第一个定理通过对逐段时间上的数量关系进1控制来给Ñ实用稳定的¿分条件;第二个定理通过对多段时间的累积?应进1控制来给Ñ实用稳定5的¿分条件.•后给Ñ了具体例f,及Ù数值模拟结果.

§2 预备知识

首先给Ñ一?记号.令R表示实数集,R+表示非负实数集,N+表示正整数集,N=N+∪ {0}, 向量M=(m1,m2,···mn)的模为

约定:对任意的φ∈PC((t0,+∞)),令

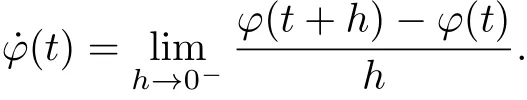
考虑m个时滞微分f系统

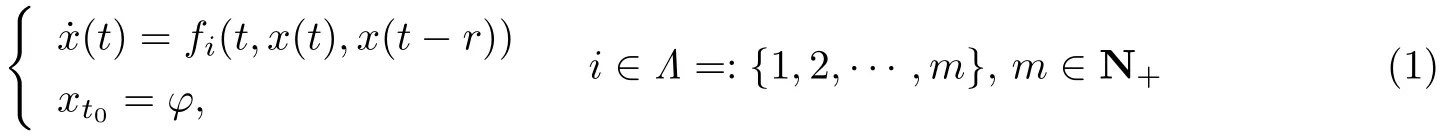
及切换模式

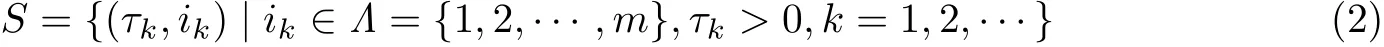
和脉À模式

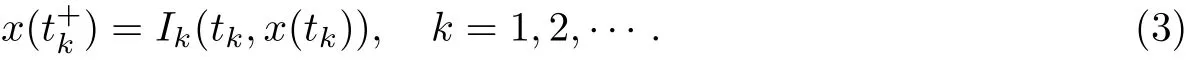
Ù中,时滞r∈R+,x∈Rn;φ∈C([−r,0],Rn),fi∈C(R+×Rn×Rn,Rn),i∈Λ.S表示切换模式,τk＞0为第ik个f系统被激活时间•度,并¡{τk}为切换时间间隔S列.对任意Ð始时刻

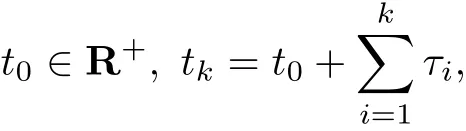
由式(1)-(3)构成时滞脉À切换系统:

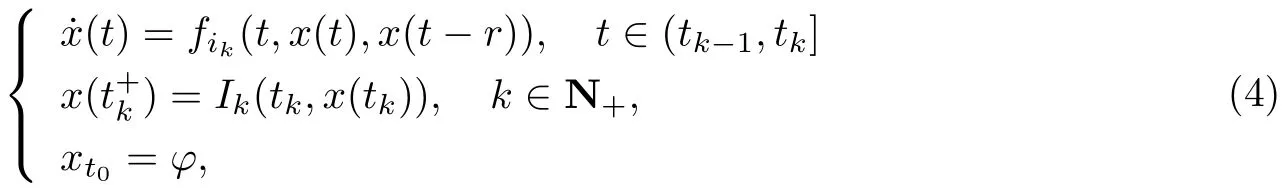
5552.1系统(4)解的•在唯一5的讨论见文[11-12],以下o假定系统(4)的解在[t0,+∞)上•在唯一.

½Â2.1如果对于给定的估计(λ,A):0＜ λ＜ A,•在t0∈R+,使得当‖φ‖＜ λ时,有|x(t,t0,φ)|＜A对所有的t≥t0成立,则¡系统(4)的零解是λ−A-实用稳定的.

½Â2.2如果对于给定的估计(λ,A):0＜ λ ＜ A,对任意t0∈R+,当‖φ‖ ＜ λ时,有|x(t,t0,φ)|＜A对所有的t≥t0成立,则¡系统(4)的零解是λ−A-一致实用稳定的.

½Â2.3函数V(t,x)÷X系统(4)中的第i个f系统˙x(t)=fi(t,x(t),x(t−r))的解x(t)的右上导数D+V(t,x)定义为:

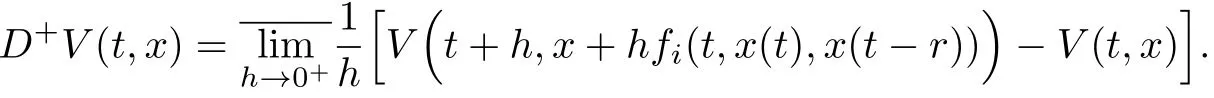
§3 主要结果

.

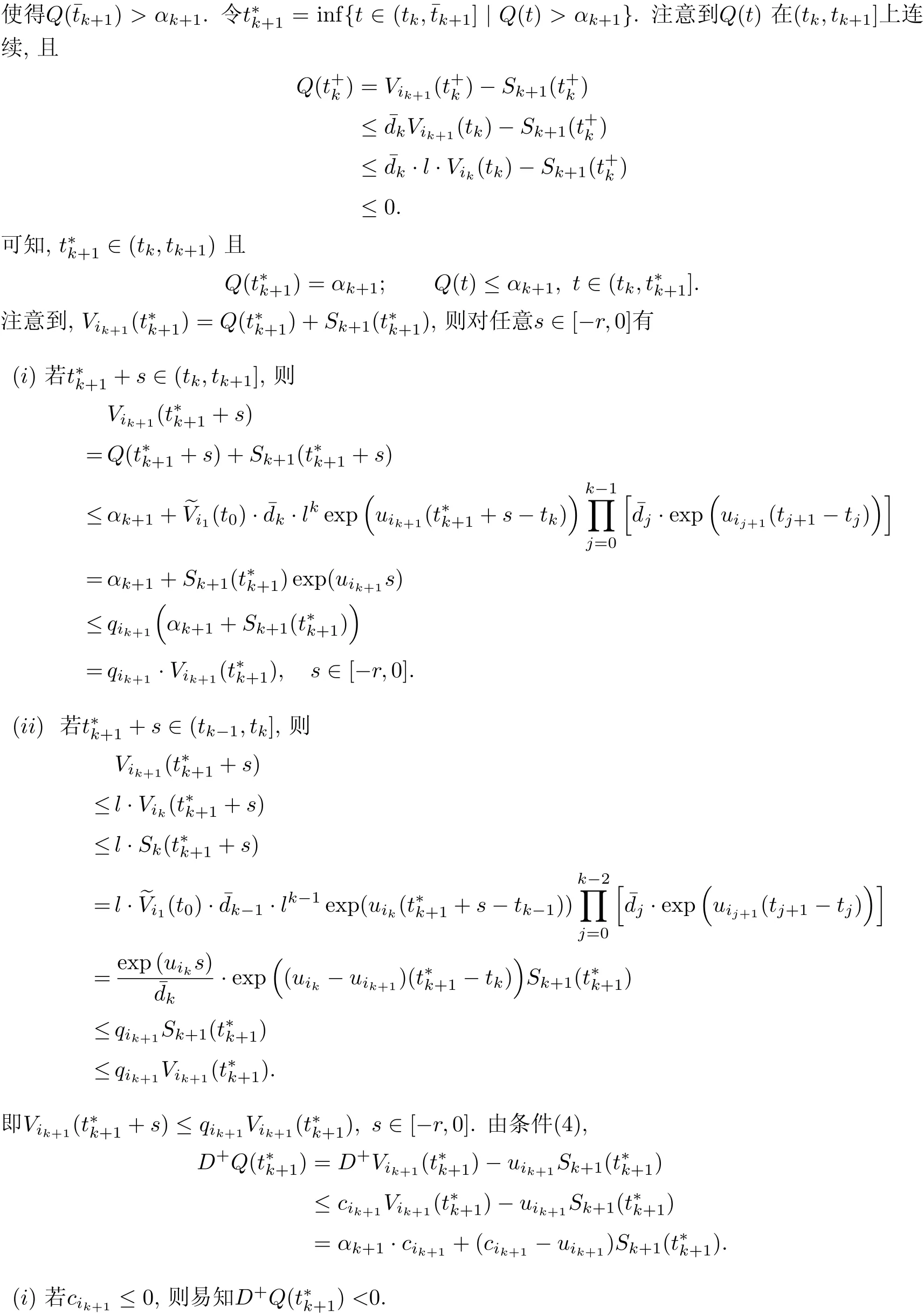
则系统(4)的零解是λ−A-实用稳定的.

推论3.3对于给定估计(λ,A):0＜λ＜A,若对任意t0∈R+定理3.1(定理3.2)中的条件均成立,则系统(4)的零解是λ−A-一致实用稳定的.

§4 应用举例

可知定理3.2的条件成立,故该系统的零解是λ−A-实用稳定的.数值模拟见图2.

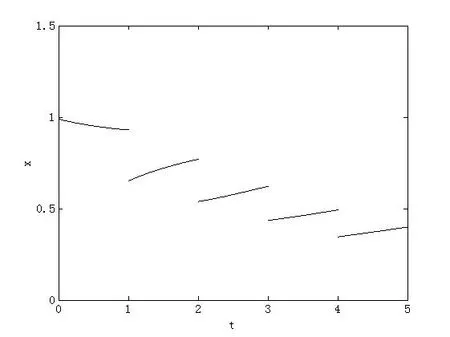
图1 t0=0,ϕ=0.99

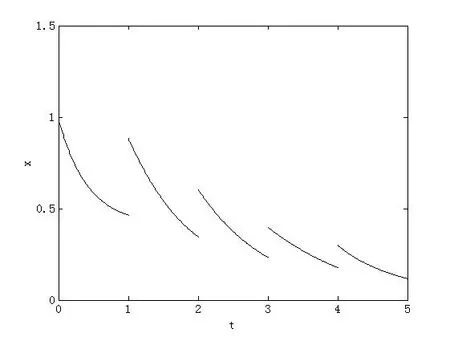
图2 t0=0,ϕ=0.99

参考文献:

[1] Chen Wuhua,Zheng Weixing.Exponential stability of nonlinear time-delay systems with delayed impulse e ff ects[J].Automatica,2011,47(5):1075-1083.

[2] Mohamad S Alwan,Xinzhi Liu.Stability of singularly perturbed switched systems with time delay and impulsive e ff ects[J].Nonlinear Analysis:Theory,Methods Appl,2009,71(9):4297-4308.

[3] Liu Yubin,Feng Weizhen.RazumikhinõLyapunov functional method for the stability of impulsive switched systems with time delay[J].Math Comput Model,2009,49:249-264.

[4] 阿·阿·玛尔德纽克,孙振绮.实用稳定5及应用[M].北京:科ÆÑ版?,2004.

[5] Liu Xinzhi.Practical Stabilization of Control Systems with Impulse E ff ects[J].J Math Anal Appl,1992,166:563-576.

[6] 杨玉华.一类非线5动力系统实用稳定域的ï究及应用[J].数Æ的实践与认识,2012,42(13):189-192.

[7] 李少娥,冯伟贞.时变脉À切换系统的实用稳定5分析[J].仲恺农业工§Æ院Æ报,2014,27(02):36-44.

[8] Li Shao’e,Feng Weizhen.Practical stability of linear switched impulsive system with time delay[J].Electron J Di ffEqu,2014,262:1-21.

[9] Wang Qing,Liu Xinzhi. Impulsive stabilization of delay di ff erential systems via the Lyapunov-Razumikhin method[J].Appl Math Lett,2007,20(8):839-845.

[10]Wang Qing,Liu Xinzhi.Exponential stability for impulsive delay di ff erential equations by Razumikhin method[J].J Math Anal Appl,2005,309:462-473.

[11]Lakshmikantham V,Liu Xinzhi.Impulsive hybrid systems and stability theory[J].Dyn Systems Appl,1998,7:1-10.

[12]Ye Sun,Anthony N.Michel,Zhai Guisheng.Stability of discontinuous retarded functional di ff erential equations with applications[J].IEEE Trans Automatic Control,2005,50(08):1090-1105.

Practical stability of impulsive switched systems with time delay by Lyapunov-Razumikhin method

LI Shao-e1,2,FENG Wei-zhen1
(1.School of Math.Sci.,South China Normal Univ.,Guangzhou 510631,China;2.Guihua High School,Foshan 528200,China)

This paper is devoted to study practical stability of the general impulsive switched systems with time delay.By employing the Razumikhin technique and Lyapunov functions,we establish some sufficient conditions to guarantee the practical stability or uniform practical stability of impulsive switched systems with time delay.Two examples and simulation are also given to illustrate our results.

impulsive switched systems with time delay;practical stability;Razumikhin-type conditions;Lyapunov function

34D99;34H15

O175

A

:1000-4424(2016)03-0327-11

2015-05-05

2016-07-28

广东省自然科学基金(S2012010010034)