一类无干涉作业的码头起重机调度问题的近似算法研究

张文帅, 张 安, 陈光亭,2, 陈 永

(1.杭州电子科技大学理学院,浙江杭州310018;2.台州学院数学与信息工程学院,浙江台州317000)

一类无干涉作业的码头起重机调度问题的近似算法研究

张文帅1, 张 安1, 陈光亭1,2, 陈 永1

(1.杭州电子科技大学理学院,浙江杭州310018;2.台州学院数学与信息工程学院,浙江台州317000)

集装箱港口上的大型货轮通常是由从船头到船尾纵向分布的集装箱船舱构成,而码头起重机主要负责装载或卸载集装箱.如何调度码头起重机在很大程度上影响着集装箱货轮的运输效率.该文主要研究一类无干涉作业的起重机调度问题,目标是极小化装(卸)载总耗时.对三台,四台起重机情形设计了新型调度算法,并给出了最坏情况分析,改进了文献中的已有结果.

码头起重机;调度;近似算法;最坏情况分析

§1 引 言

在现代物流业中,海洋运输已成为国际贸易的支柱和推动贸易全球化的关键动力.根据中国产业信息网消息,海运几乎承担了全球90%的国际贸易量,全球各大港口之间的竞争也越来越激烈.因而如何提高港口运行效率,尤其是如何减少码头起重机的装载或卸载耗时,就显得至关重.

集装箱港口上的大型货轮通常是由从船头到船尾纵向分布的集装箱船舱构成,用于装载不同目的地或不同客户需求的集装箱,而码头起重机主要负责装载或卸载集装箱,如何调度码头起重机在很大程度上影响着集装箱货轮的运输效率.为减少装卸错漏,同一船舱内的集装箱只能由一台起重机来处理.由于交叉作业会增加调度的复杂性并会产生较高的风险,所以在起重机调度过程中一般严禁两台起重机之间的交叉作业.也就是说,当其中一台起重机正在装载(卸载)某个船舱时,该起重机右侧的任何一台起重机都不允许同时处理此船舱左侧的其他船舱,同样地,该起重机左侧的任何一台起重机也不允许同时处理此船舱右侧的其他船舱,即所谓“无干涉作业”(non-interference-operation).

近年来,对于港口码头起重机的调度问题引得大家的广泛关注.对于该问题,理论上,极小化装载(卸载)总耗时的优化问题是NP-困难的[1-2].Lee[3]等人分别设计了启发式算法,遗传算法,并通过数据实验评估算法的实际性能.其他关于该问题的启发式算法研究可参考Lee和Chen[4],Guan[5]等人.Lim[6]等人则设计了动态规划算法,并给出了三个最坏情况界为2的近似算法以及一个完全多项式时间近似方案(FPTAS).Lee[2]等人给出了另一个最坏情况界为2的近似算法.Liu等人[7]则针对码头起重机的数量为2和3的情形分别设计近似算法,并证明其最坏情况界分别为4/3和5/3.Fu和Diabat[8]设计了利用拉格朗日松弛方法来求解的数学规划模型.Goodchild和Daganzo[9-10]首次对简单情形下的码头起重机的双循环调度给出了最优算法.Lee[11]等人则针对一般情形的码头起重机的双循环调度给出了最优算法,找到集装箱的最优排序.其他相关研究参看综述文献[12-13].

本文则对码头起重机数量为3和4的情形设计近似算法,并证明其最坏情况界分别为3/2和8/5.全文安排如下,§2给出本文的符号约定以及算法描述,§3为算法的最坏情况分析,§4给出主要结论.

§2 符号说明及调度算法

记船头到船尾的船舱依次为h1,h2,···,hn,令T={h1,h2,···,hn},船舱hj可装载(或需卸载)的集装箱数量为pj(＞0).在不引起混淆的情况下,也用T表示各船舱中集装箱数量的总和,对任意X⊂T,也用X表示其中的所包含的集装箱总数目,即pmax为集装箱数量最多的船舱中所包含的集装箱数量,即pmax=mjax pj.m台码头起重机依次记为QCi(i=1,2,···,m).CA为调度算法所需的装载(卸载)总耗时,C∗为最优解所需的装载(卸载)总耗时.为方便起见,假设每台起重机在单位时间内能够装载(卸载)一个集装箱.

有以上的说明,不难得到最优解的一般性质:

引理1

接下来给出调度算法,该算法首先寻找把整艘船的集装箱数量二等分的分割船舱,并根据该分割船舱两侧集装箱数量的具体情况给出各个船舱在码头起重机上的安排.“二分”调度算法A的具体描述如下(参看图1):

“二分”调度算法A

从整艘船中找到把集装箱数量二等分的船舱hm,为方便起见,

令L={h1,h2,···,hm−1},R={hm+1,···,hn}.

一 三台码头起重机情形:

分别将L分配给起重机QC1,将hm分配给起重机QC2,将R分配给起重机QC3,终止.

二 四台码头起重机情形:

1.若L∈[0,0.4T]且R∈[0,0.4T],则将L分配给起重机QC1,将hm分配给起重机QC2,将R分配给起重机QC3,终止.

2. 若L∈[0,0.4T](或R∈[0,0.4T]),则将L(R)分配给起重机QC1(QC4),将hm分配给起重机QC2(QC3),并执行子算法B(R,QC3,QC4),(B(L,QC1,QC2)),终止.

3. 若L∈(0.4T,0.45T]且R∈(0.4T,0.45T].则分别执行子算法B(L,QC1,QC2)和B(R∪{hm},QC3,QC4),终止.

4. 若L∈(0.45T,0.5T](或R∈(0.45T,0.5T]),则分别执行子算法B(L,QC1,QC2)和B(R∪{hm},QC3,QC4),(B(R,QC3,QC4)和B(L∪{hm},QC1,QC2)),终止.

子算法B(S,QCi,QCj)(i＜ j):S={hx,···,hy}(x＜y≤n),找到把S中集装箱数量二等分的船舱hs,令S1={hx,···,hs−1},S2={hs+1,···,hy},若S1≤ S2,则将S1∪ {hs}分配给起重机QCi,将S2分配给起重机QCj;否则,将S1分配给起重机QCi,将S2∪{hs}分配给起重机QCj,终止.

下面根据子算法B(S,QCi,QCj)的描述给出如下引理:

引理2对于子算法B(S,QCi,QCj)(i＜j),若S≤0.55T,则

证由子算法描述,若S1≤S2,则将S1∪{hs}分配给起重机QCi,将S2分配给起重机QCj;否则,将S1分配给起重机QCi,将S2∪{hs}分配给起重机QCj.可知S=S1+ps+S2≤0.55T,CB=min{S1,S2}+ps,若CB=min{S1,S2}+ps≤0.4T,则由引理1可得:若CB=min{S1,S2}+ps＞ 0.4T,即S1+ps＞ 0.4T,S2+ps＞ 0.4T成立.而S1+ps+S2≤ 0.55T,故有S1＜ 0.15T,S2＜ 0.15T,进而有ps＞ 0.25T.由引理1可得:

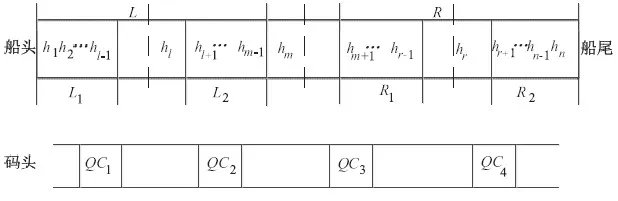
图1 船舱与码头起重机的分布情况及分割船舱

§3 最坏情况分析

定理1对于三台码头起重机,“二分”调度算法A的最坏情况界不超过3/2,且是紧的.

证根据算法A的三台码头起重机情形的描述:分别将L分配给起重机QC1,将hm分配给起重机QC2,将R分配给起重机QC3,则有:CA=max{L,pm,R}.

情形1: 若CA=pm,由引理1可得:

情形2: 若CA=max{L,R},由引理1可得：

下面给出紧例:T=6,其中L=2,pm=1,R=3.L是有两个含有相等数量集装箱的船舱构成,R是有三个含有相等数量集装箱的船舱构成.此例根据三台码头起重机的算法描述,可知CA=3.最优解中,三台机首先共同装(卸)载R,然后将L分配给QC1,QC2,将pm分配给QC3装(卸)载,此时C∗=2,因此

定理2对于四台码头起重机,“二分”调度算法A的最坏情况界不超过8/5,且是紧的.

证 情形1:由算法描述可得:CA=max{L,pm,R}.

情形1.1:CA=pm,由引理1可得:

情形1.2:CA=max{L,R},由引理1可得：

情形2: 若L∈[0,0.4T],由算法描述可得：CA=max{L,pm,min{R1,R2}+pr}.

情形2.1:CA=L,由引理1可得:

情形2.2:CA=pm,由引理1可得:

情形2.3:CA=min{R1,R2}+pr,由于执行子算法B(R,QC3,QC4),此时S=R≤0.5T＜0.55T,由引理2可得:

同理可证R∈[0,0.4T]的情形.

情形3:由算法描述可得:CA=max{min{L1,L2}+pl,min{R1,R2}+pr}.

情形3.2:CA=min{R1,R2}+pr,由算法A执行子算法B(R∪{hm},QC3,QC4),此时0.55T＜S=R+pm＜0.6T,进一步分析:

情形3.2.1:CA=min{S1,S2}+ps≤0.4T.则由引理1可得：.

情形3.2.2:CA=min{S1,S2}+ps＞ 0.4T.即S1+ps＞ 0.4T,S2+ps＞ 0.4T成立.由(1),可得:S1＜0.2T,S2＜0.2T.进而有ps＞0.2T.故下式成立:

考虑问题最优解:若hs分配给QC4,即当QC4正在装(卸)载hs时,由于无干涉作业,hs右侧的所有船舱S2不能够被其他三台起重机处理,由四台起重机同时处理S2时,至少耗时故

若hs分配给QC3,即当QC3正在装(卸)载hs时,QC4装(卸)载S2提前完工,由于无干涉作业,QC4需要等待QC3装(卸)载hs完成时才能继续工作,故

若hs分配给QC2,即当QC2正在装(卸)载hs时,QC3,QC4同时装(卸)载S2提前完工,由于无干涉作业,QC3,QC4需要等待QC2装(卸)载hs完成时才能继续工作,故

同理,若hs分配给QC1,则故有:.

下面考虑CA:

(5)可靠性原则。系统应满足电网企业运营监测业务应用24小时可靠运行的要求，系统关键环节软硬件资源设计采用高可用方案，保证系统运行的高度可靠，避免出现数据不及时和信息失真等现象。

情形3.2.2.1: 若S1≤S2,则CA=S1+ps.

情形3.2.2.2: 若S1＞S2,则CA=S2+ps.

情形4: 若L∈(0.45T,0.5T],由算法描述可得:CA=max{min{L1,L2}+pl,min{R1,R2}+pr}.若CA=min{L1,L2}+pl,由执行子算法B(L,QC1,QC2),此时S=L≤0.5T＜0.55T.故由引理2得：若CA=min{R1,R2}+pr,由执行子算法B(R∪{hm},QC3,QC4),此时S=R+pm＜0.55T.故由引理2得:

同理可证R∈(0.45T,0.5T]的情形.

下面给出紧例:T=10,其中L1=L2=pm=R1=R2=2.L1是有四个含有相等数量集装箱的船舱构成.此例根据四台码头起重机的算法描述在第1步终止,可知CA=4.最优解中,四台机首先共同装(卸)载L1,然后将L2,pm,R1,R2分别分配给QC1,QC2,QC3,QC4装(卸)载,此时C∗=2.5,因此

§4 结论

本文研究了在港口码头无干涉作业的小数量码头起重机调度问题,主要针对三台及四台码头起重机的情况给出了最坏情况界分别为3/2和8/5的近似算法,并给出紧例,这是全新的结果.如何将上述调度算法的设计思想推广到任意m台码头起重机的情形,以及如何考虑具有不同速率的码头起重机调度问题,将是本文的进一步研究方向.

[1] Lim A,Rodrigues B,Xu Zhou.A m-parallel crane scheduling problem with a non-crossing constraint[J].Naval research logistics,2007,54(2):115-127.

[2] Lee D H,Wang Huiqiu,Miao Lixin.An approximation algorithm for quay crane scheduling with non-interference constraints in port container terminals[R].Technical Report,presented at Tristan VI,Phuket,June 10-15,2007.

[3] Lee D H,Wang Huiqiu,Miao Lixin.Quay crane scheduling with non-interference constraints in port container terminals[J].Transportation Research Part E:Logistics and Transportation Review,2008,44(1):124-135.

[4] Lee D H,Chen Jianghang.An improved approach for quay crane scheduling with noncrossing constraints[J].Engineering Optimization,2010,42(1):1-15.

[5] Guan Yongpei,Yang K H,Zhou Zhili.The crane scheduling problem:models and solution approaches[J].Annals of Operations Research,2013,203(1):119-139.

[6] Lim A,Rodrigues B,Xu Zhou.Approximation schemes for the crane scheduling problem[A].In:Hagerup T,Katajainen J,eds,9th Scandinavian workshop on algorithm theory(SWAT 2004)[C].Lecture notes in computer science,vol.3111,2004,323-335.

[7] Liu Ming,Zheng Feifeng,Li Jinfeng.Scheduling small number of quay cranes with noninterference constraint[J].Optimization Letters,2015,9(2):403-412.

[8] Fu Yimin,Diabat A.A Lagrangian relaxation approach for solving the integrated quay crane assignment and scheduling problem[J].Applied Mathematical Modelling,2015,39(3):1194-1201.

[9] Goodchild A V,Daganzo C F.Double-cycling strategies for container ships and their e ff ect on ship loading and unloading operations[J].Transportation Science,2006,40(4):473-483.

[10]Goodchild A V,Daganzo C F.Crane double cycling in container ports:planning methods and evaluation[J].Transportation Research Part B:Methodological,2007,41(8):875-891.

[11]Lee C Y,Liu Ming,Chu Chengbin.Optimal Algorithm for the General Quay Crane Double-Cycling Problem[J].Transportation Science,2014:1-11.

[12]Bierwirth C,Meisel F.A survey of berth allocation and quay crane scheduling problems in container terminals[J].European Journal of Operational Research,2010,202(3):615-627.

[13]Bierwirth C,Meisel F.A follow-up survey of berth allocation and quay crane scheduling problems in container terminals[J].European Journal of Operational Research,2015,244(3):675-689.

Approximation algorithms of quay crane scheduling with non-interference constraints

ZHANG Wen-shuai1,ZHANG An1,CHEN Guang-ting1,2,CHEN Yong1
(1.School of Science,Hangzhou Dianzi Univ.,Hangzhou 310018,China;2.School of Math.&Inform.Engine.,Taizhou Univ.,Taizhou 317000,China)

In port container terminals,a vessel is usually divided longitudinally between head and tail into many holds to store containers,which must be loaded or unloaded by several quay cranes.The scheduling of quay cranes signi fi cantly in fl uences the turn-around time of a container vessel.This paper studies a problem of scheduling small number of quay cranes with non-interference constraint.The objective is to minimize the overall time of loading or unloading the containers.New scheduling algorithms are designed and analyzed for three and four quay cranes,which improve previous results on this problem.

quay cranes;scheduling;approximation algorithm;worst-case analysis

90B35;68W25

O221.7

A

:1000-4424(2016)03-0351-06

2016-03-07

2016-05-06

国家自然科学基金(11571252;11201105;11401149);浙江省自然科学基金(LY16A010015)