具有风险偏好的梯形直觉模糊双矩阵对策模型及解法

杨 洁,李登峰,赖礼邦

(1.福建农林大学管理学院,福建福州350002;2.福州大学经济与管理学院,福建福州350116;3.福建船政交通职业学院,福建福州350007)

具有风险偏好的梯形直觉模糊双矩阵对策模型及解法

杨 洁1,李登峰2,赖礼邦3

(1.福建农林大学管理学院,福建福州350002;2.福州大学经济与管理学院,福建福州350116;3.福建船政交通职业学院,福建福州350007)

在对策问题中,行动方案的选择不可避免的需要对预期支付值(收益值)进行估计和排序,且选择结果往往受到现实局中人风险偏好程度的影响.因此,该文针对局中人具有风险偏好及支付值为梯形直觉模糊的双矩阵对策进行了模型及求解方法的探讨.首先,提出了具有风险偏好的梯形直觉模糊数排序方法,再利用双线性规划求解方法,对梯形直觉模糊双矩阵对策进行求解.最后以企业营销策略选择为例,表明了该方法的有效性和实用性.

双矩阵对策;梯形直觉模糊数;风险偏好;排序方法

§1 引 言

矩阵对策作为一种研究相互作用策略的重要理论,已广泛应用于不同领域.在现实运用中,由于信息的不充分或不准确,局中人无法准确得知对策收益值(支付值),局中人支付应采用近似估计值而不是精确值[1-3].但已有模糊矩阵对策研究主要是利用Zadeh[4]提出的模糊集理论研究对策论中的模糊性或模糊现象,如策略集、收益矩阵由模糊集来描述.然而,模糊集是用单一的隶属度同时表示模糊概念或模糊现象的两个对立面(即“非此即彼”).因此该模糊状态仅限于“绝对肯定”和“绝对否定”,无法刻画一定程度的犹豫不确定性.Atanassov[5]提出的两标度(隶属度和非隶属度)直觉模糊集(Intuitionistic fuzzy sets)能很好实现“非此非彼”性,能同时表示肯定程度、否定程度和犹豫程度三种状态信息,在处理不确定性方面更具灵活性和实用性[6-7].因此,研究支付值为直觉模糊集的对策具有十分重要的理论与应用价值.

通过对比研究发现,用直觉模糊集研究对策和用模糊集研究对策在研究方法与内容上有很大的不同:前者运用两标度直觉模糊集解决对策问题中的模糊性,而后者运用单标度模糊集;前者在解决对策问题时需要进行相互冲突的两标度大小比较即向量(由隶属度与非隶属度组成)间的比较,而后者进行的是单标度大小比较即实数(隶属度)间的比较[7-9].正是这些差异决定了用直觉模糊集研究对策问题会不可避免的出现截然不同的根本性问题,因此需要专门研究能有效解决直觉模糊博弈问题的理论与方法.

目前,模糊矩阵对策的研究主要集中在均衡解的定义、性质以及求解模型和方法,其主要思想是根据模糊矩阵对策解的定义建立模糊数学规划模型,然后通过模糊数的特殊处理,尤其是排序处理,将模糊数学规划转化为经典的数学规划,进而得到模糊矩阵对策的解.其中,Campos[10]率先基于模糊数排序函数和辅助线性规划模型提出了解决模糊矩阵对策的方法;Bector等[11]在Campos基础上提出了基于对偶线性规划和模糊参数的模糊矩阵对策的线性规划求解方法;Vijay等[12]利用模糊数的排序方法,提出了目标模糊且支付模糊的双矩阵对策的方法;Meada[13]通过模糊数的可能性测度,提出了具有模糊支付的双矩阵对策均衡解.可见,模糊量排序问题对于研究模糊对策问题具有十分重要的意义.

此外,在现实的行动方案选择中,局中人的个体差异普遍存在,如局中人偏好的不同.本文将融合联盟中各局中人的不同偏好信息于直觉模糊矩阵对策中,提出了一种考虑局中人风险偏好的梯形直觉模糊数的矩阵对策模型及解法,使得研究更贴近于现实应用背景.

§2 梯形直觉模糊数及其排序方法

局中人对行动方案的选择,需要对不同行动的预期支付值进行比较,这将涉及到模糊量的排序.然而,目前有关梯形直觉模糊数的排序并没有给出有效的方法.因此,本文首先确定梯形直觉模糊数的排序问题.

2.1 梯形直觉模糊数的定义和运算

其中,w和u表示最大的隶属度和最小的非隶属度,满足0≤w≤1,0≤u≤1,0≤w+u≤1.此外,π(x)=1−µ(x)−υ(x),π(x)为梯形直觉模糊数的直觉模糊指标,它反映了x属于的犹豫程度.特别地,若a1=a2,则退化为一个三角直觉模糊数;若同时成立,则退化为一个区间直觉模糊数.由此可见,常见的区间直觉模糊数,三角直觉模糊数都是梯形直觉模糊数的特例.

其中,符号“∧”和“∨”分别表示取最大值或最小值.

定义1设〉为梯形直觉模糊数,定义为梯形直觉模糊数的α截集,为梯形直觉模糊数的β截集,其中0≤α≤w,u≤β≤1且0≤α+β≤1.两截集均为闭区间,记α截集为,记β截集为其计算分别为

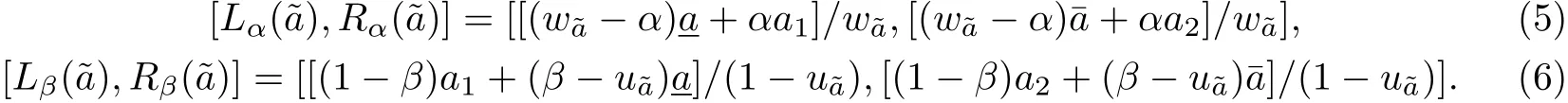
2.2 梯形直觉模糊数的排序方法

定义2设分别为梯形直觉模糊数的α截集和β截集，梯形直觉模糊数关于隶属度µ(x)和非隶属度υ(x)的值分别定义为

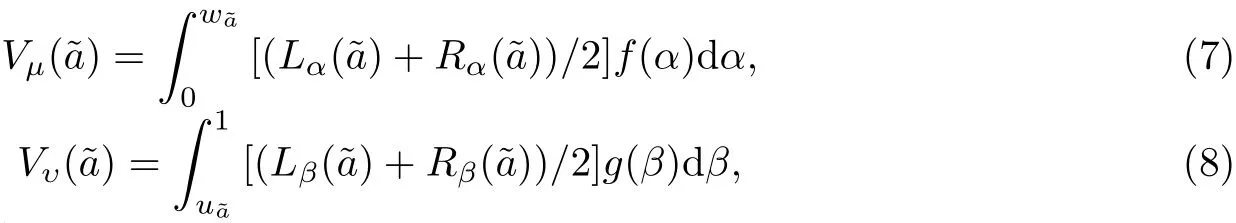
其中,f(α)(α∈[0,w])是非负递增函数,且f(0)=0,f(w=1;g(β)(β∈[u,1])为非负递减函数,且g(u)=1,g(1)=0.f(α)和g(β)分别表示对不同的α截集和β截集赋予不同的权重.Jafarian和Rezvani[14]对函数f(α)和g(β)的具体形式及运用情况给出了较多详细解释.本文以f(α)=α/w,g(β)=(1−β)/(1−u)为例主要因为其满足单调性且形式简单,便于进行理论分析.在实际应用中,可根据实际情况选择f(α)和g(β).此外,综合反映了隶属度的信息,可以看成是隶属度所表示的梯形直觉模糊数的中心值(central value)[15];综合反映了非隶属度的信息,可以看成是非隶属度所表示的梯形直觉模糊数的中心值.

定义3设分别为梯形直觉模糊数〉的α截集和β截集,梯形直觉模糊数关于隶属度µ(x)和非隶属度υ(x)的模糊度分别定义为

定义4〉是梯形直觉模糊数,的值指标和模糊度指标分别定义为

其中,λ∈[0,1]表示了局中人的风险偏好信息.λ∈[1/2,1]表明局中人偏好积极乐观的正面信息,即更关注不确定量的满意程度;λ∈[0,1/2]表明局中人偏好悲观否定的负面信息,即更关注不确定量的不满意程度.因此,值指标和模糊度指标可以反映决策者对梯形直觉模糊数的主观态度.此外,当λ∈[0,1]一定时,根据式(15)和式(16)可知是关于风险偏好λ∈[0,1]的线性连续函数.

定义5〉为2个梯形直觉模糊数,根据梯形直觉模糊数的值指标和模糊度指标定义其排序方法为

2.3 梯形直觉模糊数排序方法合理性检验

尽管目前已有的排序方法很多,但由于每个排序指标都是从不同的侧面来描述模糊量的状态,具都有一定的片面性,尚无一种为大家普遍接受的方法.因此,研究者开始研究这些排序方法的合理性问题.Wang和Kerre[16]根据模糊量的数学含义及决策实际问题要求，提出了评价模糊数排序方法合理性的一系列公理化标准,以此来衡量模糊集的排序方法.本文所提方法至少满足评价模糊数排序方法合理性的7个公理化标准中的5个公理.

公理1排序关系的自反性:对任意梯形直觉模糊数满足

公理2排序关系的等价性:对任意梯形直觉模糊数和˜b,若则有

公理3排序关系的传递性:对任意的梯形直觉模糊数则有

公理4不相关模糊量的独立性:对任意两个有限子集F1和F2的梯形直觉模糊数,任意梯形直觉模糊数∈F1∩F2且∈F1∩F2,当且仅当在F2上成立,则有在F1上成立;

公理5加法的相容性:对任意的梯形直觉模糊数满足w=w˜b且u=u˜b,若则有

此外,该排序方法综合了值指标和模糊度指标,具有良好性质,特别是线性性质,优于较多现存方法[17-18].综上所述,当λ∈[0,1],对任意两个梯形直觉模糊数和

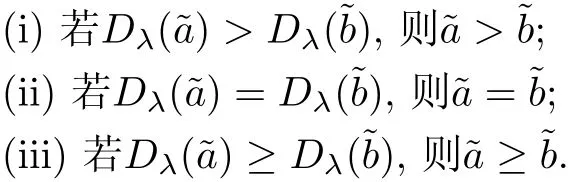
§3 具有风险偏好的梯形直觉模糊双矩阵对策模型及解法

3.1 梯形直觉模糊双矩阵对策模型

当局中人p1选取纯策略αi∈S1(i=1,2,···,m),局中人p2选取纯策略βj∈S2(j=1,2,···,n)时,局中人p1和p2获得的支付值分别表示为梯形直觉模糊数

即局中人p1和p2在所有局势下的支付值可分别直观地用矩阵表示为:简洁表示为

当局中人p1选择混合策略y∈Y,局中人p2选择混合策略z∈Z,局中人p1的期望支付值为根据梯形直觉模糊数的运算法则,有

类似的,局中人p2的期望支付值˜E2(y,z)为:

其中(y,z)表示同一个混合策略,且支付值都为梯形直觉模糊数.

定义6设有一局势为(y∗,z∗)∈Y×Z.若对局中人P1和P2的所有混合策略y∈Y与z∈Z,都满足,则称(y∗,z∗)为双矩阵对策的均衡点或Nash解,y∗与z∗分别称为局中人P1和P2的均衡策略,并称分别为P1,P2的均衡解.

3.2 梯形直觉模糊双矩阵对策求解方法

双矩阵博弈的Nash均衡的求解可以转化为一个二次规划问题的求解.假设(A,B)为任意双矩阵对策,(y∗T,z∗T,u∗,v∗)为双矩阵对策的一个Nash均衡解,该均衡解可通过求解以下线性规划模型获得.但由于本文局中人p1和p2的期望支付值值都为梯形直觉模糊数,无普遍使用的解概念.此外,由于梯形直觉模糊数的隶属度和非隶属度计算问题,使得均衡策略和均衡解不易求解.因此,根据本文引入的排序函数,提出一种带风险偏好的梯形直觉模糊双矩阵对策求解方法.

根据式(17),局中人p1和p2的期望支付值可转化为带参数的双矩阵对策,表示为

通过以下带参数双线性规划模型,可求解(y∗,z∗,u∗(λ),v∗(λ)),线性规划构造如下:

且y∗T

§4 运用实例

现有公司M1和M2欲占领某一产品市场,各自拟定下一年度产品的销售计划,以便增加自己产品在该市场上的销售量.公司M1考虑采用下面的2种策略来增加自己产品在该市场上的销售量:策略α1(加大产品广告宣传),策略α2(改进产品包装).公司M2考虑采用同样的策略来增加自己产品在该市场上的销售量,即策略β1(加大产品广告宣传),策略β2(改进产品包装).两家公司市场产品销售策略的选择问题可以看作是1个双矩阵对策问题,其中公司M1和M2可分别看作是2个局中人P1和P2.由于市场环境的复杂性和信息的不确定性,2家公司的管理者很难精确估计下一年度各种情形(或局势)下产品销售量的具体结果,只能给出近似值,并且带有一定的不确定性即犹豫程度.公司M1和M2在所有4种情形(或局势)下的支付值可表示为下面的梯形直觉模糊数矩阵

式中,〈(70,80,90,100);0.8,0.1〉为梯形直觉模糊数,表示当公司M1和M2都采用“加大产品广告宣传”策略时,公司M1的产品销售量约在70-100(万单位)之间;对于这个近似估计值公司(决策者)最大的满意度为0.8,最小的不满意度为0.1,犹豫度为0.1.矩阵中其它的梯形模糊数可做类似的解释.试用本文双矩阵对策方法确定2家公司的最优策略.

当两公司(决策者)的风险偏好程度不同,即对应不同参数λ1∈[0,1]和λ2∈[0,1],可根据式(11)-(17),求得公司M1和M2的模糊预期支付值指标和模糊度指标之间的差异程度,分别为:

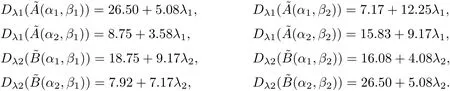
根据式(18),求解该矩阵对策的双线性规划模型如下:

当两公司的风险偏好程度不同,即对应不同参数λ1∈[0,1]和λ2∈[0,1],可通过求解式(19),求得Nash均衡支付值和对应的最优策略.如下表列举:

表1 两公司的Nash均衡支付值和对应的最优策略

两公司的Nash均衡支付值和对应的最优策略仅列举部分(限于篇幅问题),通过对不同风险偏好λ计算结果比较分析得到:任一局中人的满意期望支付值与自身的风险偏好程度密切相关,两者呈现正相关关系,即决策者自身的风险偏好值越大,其最优期望支付值越大.此外,任一局中人的最优策略选择也与对方的风险偏好程度密切相关,两者呈现反相关关系,即对方的风险偏好值越大,决策者自身的最优策略值越小.由此可见,在进行行动方案选择过程中,不可忽视所有局中人的风险偏好程度.本文选择市场销售策略作为可能应用实例进行说明,但该方法同样适用于其他类似竞争性决策或对策问题.

§5 结束语

由于行动方案的选择不可避免的需要对预期支付进行估计和排序,本文以梯形直觉模糊数排序为基础,提出了具有风险偏好且支付值为梯形直觉模糊数的双矩阵对策及求解方法.此方法可明确局中人不同风险态度对最优策略及最优期望支付的影响,有利于最优策略的选择,且由于梯形直觉模糊数是直觉模糊数的重要推广形式,因此本文方法适用于其它形式直觉模糊数矩阵对策问题.今后,将进一步研究其它更贴近现实的直觉模糊集矩阵对策问题.

[1] Li Dengfeng.Linear programming approach to solve interval-valued matrix games[J].Omega,2011,39(6):655-666.

[2] Liu Shiang Tai,Kao Chiang.Matrix games with interval data[J].Computers&Industrial Engineering,2009,56(4):1697-1700.

[3] Nayak P K,Pal M.Linear programming technique to solve two person matrix games with interval pay-o ff s[J].Asia-Paci fi c Journal of Operational Research,2009,26(2):285-305.

[4] Zadeh L A.Fuzzy sets[J].Information and Control,1965,8:338-356.

[5] Atanassov K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,50:87-96.

[6] Li Dengfeng.Decision and Game Theory in Management with Intuitionistic Fuzzy Sets[M].Berlin:Springer,2014.

[7] Bandyopadhyay S,Nayak P K,Pal M.Solution of matrix game with triangular intuitionistic fuzzy pay-o ffusing score function[J].Open Journal of Optimization,2013,02:9-15.

[8] Nan Jiangxia,Li Dengfeng.Linear programming technique for solving interval-valued constraint matrix games[J].Journal of Industrial and Management Optimization,2014,10(4):1059-1070.

[9] 杨洁,李登峰.求解梯形模糊矩阵对策的线性规划新方法[J].控制与决策,2015,30(7):1219-1226.

[10]Campos L.Fuzzy linear programming problems to solve fuzzy matrix games[J].Fuzzy Sets System,1989,32:275-289.

[11]Bector C R,Chandra S,Vijay V.Duality in linear programming with fuzzy parameters and matrix games with fuzzy pay-o ff s[J].Fuzzy Sets System,2004,46(2):253-269.

[12]Vijay V,Chandra S,Bector C R.Bi-matrix games with fuzzy goals and fuzzy payo ff s[J].Fuzzy Optimization and Decision Making,2004,3:327-344.

[13]Maeda T.On characterization of equilibrium strategy of the bi-matrix game with fuzzy payo ff s[J].Journal of Mathematical Analysis and Applications,2000,251(2):885-896.

[14]Jafarian E,Rezvani M A.A valuation-based method for ranking the intuitionistic fuzzy numbers[J].Journal of Intelligent&Fuzzy Systems,2012(23):1-12.

[15]Yang Jie,Li Dengfeng.An e ff ective ranking method of trapezoidal intuitionistic fuzzy numbers[A].2013 International Conference on Industrial Engineering and Management Science[C].Shanghai,2013.

[16]Wang Xuzhu,Kerre E E.Reasonable properties for the ordering of fuzzy quantities(I)[J].Fuzzy Sets and Systems,2001,118(3):375-385

[17]徐泽水,达庆利.区间数排序的可能度法及其应用[J].系统工程学报,2003,18(1):67-70.

[18]Wan Shuping,Dong Jiuying.A possibility degree method for interval-valued intuitionistic fuzzy multi-attribute group decision making[J].Journal of Computer&System Sciences,2014,80(1):237–256.

Trapezoidal intuitionistic fuzzy bi-matrix game model with risk preference and its solving method

YANG jie1,LI Deng-feng2,LAI Li-bang3
(1.College of Management,Fujian Agriculture and Forestry University,Fuzhou 350002,China;2.School of Economics and Management,Fuzhou University,Fuzhou 350116,China;3.Fujian Chuanzheng Communications College,Fuzhou 350007,China)

In the process of strategy choice problem,players need to estimate and rank the expected return(payo ff s),and the selected results are often in fl uenced by risk preferences in reality.So a method for trapezoidal intuitionistic fuzzy bi-matrix game with risk preference is researched in this paper.In this method,a new order relation with risk preference of trapezoidal intuitionistic fuzzy number based on the di ff erence-index of value-index is proposed,and then the parametric bi-matrix game model is solved by bilinear programming.Lastly,the method proposed is demonstrated by a real example of the marketing enterprises’strategy choice problem,which shows the e ff ective and practical of the method.

bi-matrix game;trapezoidal intuitionistic fuzzy number;risk preference;ranking method

91A40

O225

A

:1000-4424(2016)03-0357-09

2015-11-23 修改日期:2016-04-15

国家自然科学基金重点项目(712310003);国家自然科学基金(71561008);福建省自然科学基金(2016J05169);福建省中青年教师教育科研(JAS160153)