对流占优扩散方程的分裂特征混合有限元方法

张建松, 张月芝,朱 江, 羊丹平

(1.中国石油大学(华东)应用数学系,山东青岛266580;2.巴西国家科学计算实验室,巴西里约热内卢25651-075;3.华东师范大学数学系,上海200062)

对流占优扩散方程的分裂特征混合有限元方法

张建松1, 张月芝1,朱 江2, 羊丹平3

(1.中国石油大学(华东)应用数学系,山东青岛266580;2.巴西国家科学计算实验室,巴西里约热内卢25651-075;3.华东师范大学数学系,上海200062)

利用修正的特征线方法,构建一类求解对流占优扩散方程的分裂特征混合有限元算法.在新的算法中,混合系统的系数矩阵对称正定,且原未知函数u与流函数σ=−ε∇u可分离求解.推导了加权能量模意义下的最优阶误差估计,并给出数值算例验证理论上的分析结果.

混合有限元;特征线方法;分裂解;对称正定系统;对流占优扩散方程

§1 引 言

众所周知,对流-扩散方程在科学工程中有着广泛的应用.例如,它描述了地下水中溶质的传输,油藏问题中的石油驱动,空气动力学中空气的运移以及混溶驱动流的流动等等.

特征线方法是一种能够较好地求解对流扩散问题的数值方法.许多科研人员对此方法做了大量的研究工作,见参考文献[1-14].其中,Douglas和Russell在文献[1]中首次提出了特征有限元和特征有限差分法求解对流扩散方程.之后Suli[2]和Pironneau[3-4]将此方法推广应用到Navier-Stokes方程;Russell在文献[5]中用此方法求解多孔介质中混溶驱动问题;朱江研究了KdV方程和RLW方程的特征有限元方法.为了得到质量守恒的特征有限元格式,Douglas,Huang和Pereira在文献[10]中给出了一种对流校正的修正特征有限元算法,Wang在[11]中研究了此类方法一致收敛性.对于特征混合有限元算法,也有大量的文献可供参考,见[15-18].然而,经典的混合有限元方法通常导致鞍点问题,这使得混合系统因失去对称正定性而给计算带来许多困难.

本文的主要目的就是建立一类新型分裂特征混合有限元方法求解对流占优扩散方程.算法将分裂混合有限元技巧(见文献[13,19])与修正的特征线方法(MMOC)及对流校正的修正特征线方法(MMOCAA)相结合,得到的新混合系统系数矩阵对称正定,且原未知函数u与新引入函数σ可分开求解.研究了算法的收敛性并给出了ε一致最优误差估计.

本文结构安排如下:首先在§2形成新型分裂特征混合有限元算法求解对流占优扩散方程;之后在§3中分析算法的收敛性并给出相应的误差估计;最后在§4中给出数值算例验证理论上的分析结果.

§2 算法形成

通篇文章,将用到Sobolev空间中的一些常规定义,符号,见文献[20].K无论是否带有下标,在此文章中都代表某个常数,不同地方出现时取值可能不同.

考虑如下的对流占优扩散问题:

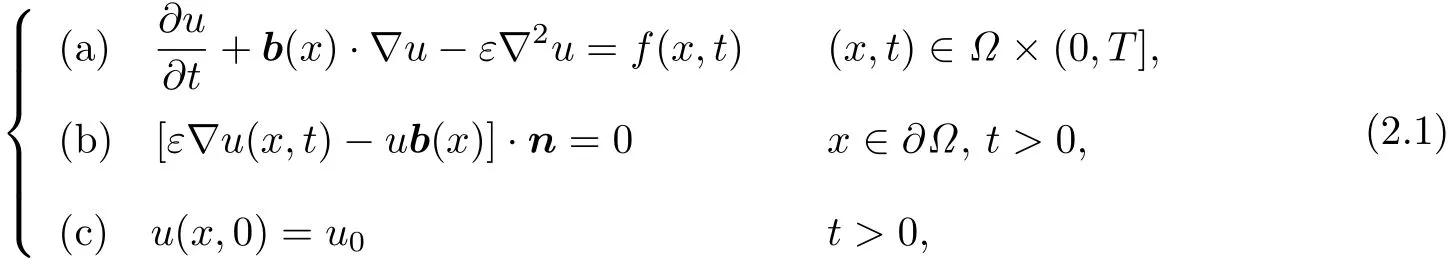
其中Ω是R2中的一有界区域,边界记为∂Ω,n为边界∂Ω的单位外法向;f(x,t)表示某个已知函数;b(x)=(b1(x),b2(x))为速度函数并假设它是不可压缩的,即∇·b(x)=0,当扩散系数0＜ε0≤ε≪1,方程(??a)则对流严格占优.为了分析方便，这里假定系数b(x)充分光滑,扩散系数ε为常数.

下面引入所谓的特征线方法.令

令σ=−ε∇u.方程(??)重写为

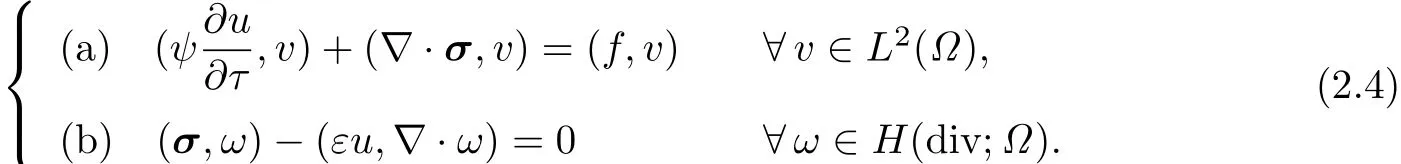
设Nt为一正整数,△t=T/Nt为时间步长.对任意的函数w用wn表示其在时刻t=tn=n△t,(n=0,...,Nt)处的值.设Thu和Thσ为区域Ω的两个拟正则剖分类,他们可能相同也可能不同,且剖分单元直径分别以hu和hσ为界.设Mhu⊂H1(Ω)和Vhσ⊂ H(div;Ω)分别为定义在剖分Thu和Thσ上的有限元空间.

下面分别给出两种分裂特征混合有限元算法.

2.1 SMMOC-MFE算法

2.2 SMMOCAA-MFE算法

文献[10]中的MMOCAA算法主要目的是消除文献[1]中MMOC算法引起的质量损失.对于方程(??a),运用修正的特征线∫方 法逼近解∫可得质量守恒∫方程

从上面的算法可以看到,混合系统的系数矩阵对称正定,并且原函数与引入的流函数可以分开求解.显然经典混合有限元方法中要求的LBB条件,这里不再是必须的条件.从计算的角度,空间Vhσ可以选择一般的连续有限元空间.在接下来的分析中，为了理论分析的方便以及推导算法的最优阶误差估计,仍然选择Vhσ为经典的混合有限元空间.

定理2.1SMMOC-MFE算法和SMMOCAA-MFE算法存在唯一解.

其中0＜ K0≤ min(1,△tε).从而可知,矩阵A和B对称正定,故而系统(??)有唯一解.进而SMMOC-MFE算法有唯一解.同理可证SMMOCAA-MFE有唯一解.

§3 收敛性分析及误差估计

假设有限元空间Vhσ和Mhu有如下的逆估计性和逼近性质(见文献[21]):存在某些常数r,r1,k＞0,使得对1≤q≤∞和任意的ω∈H(div;Ω)∩[Wr+1,q(Ω)]2,

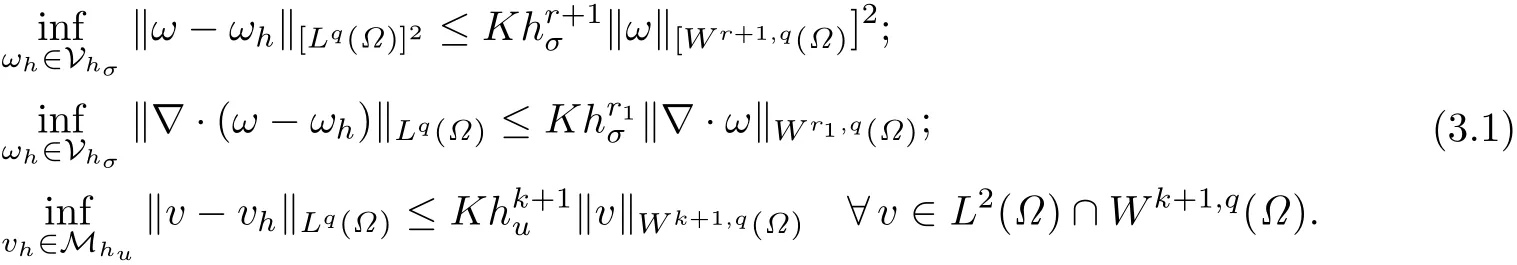
为了分析算法的收敛性,假定Vhσ为文献[21]中提到的任一经典混合有限元空间,并引入两个投影算子.众所周知，在经典的混合有限空间中,存在一个投影算子Πh:H(div;Ω)→Vhσ使得对任意的1≤q≤∞,满足

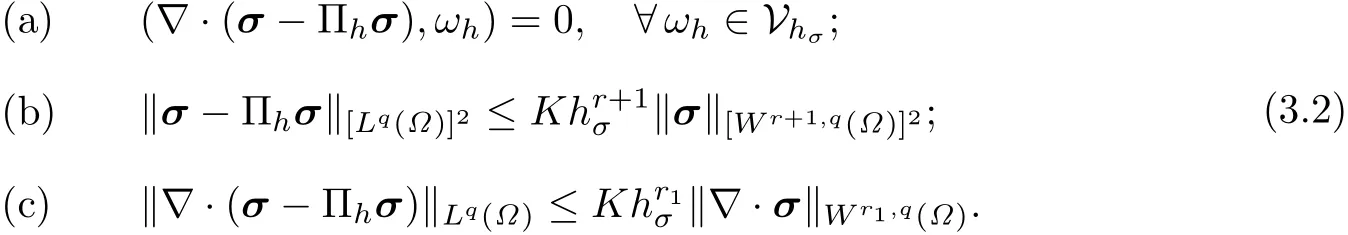
同时定义椭圆投影算子PM:H1(Ω)→Mhu满足

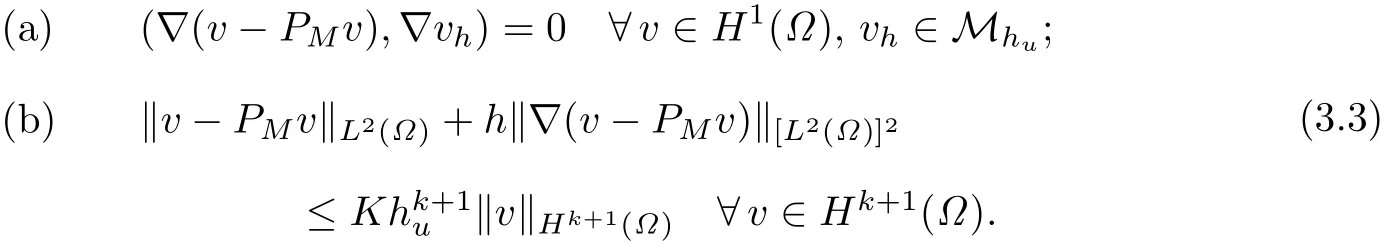
定理3.1假设问题(??)的解(u,σ)有如下的正则性:

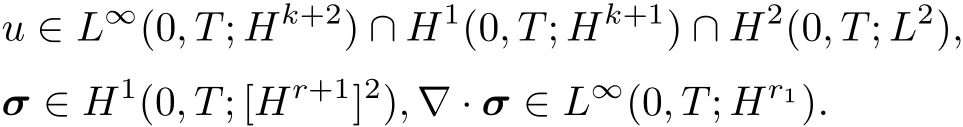
则对于SMMOC-MFE算法,有先验误差估计

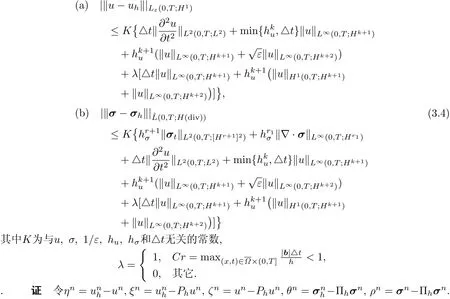
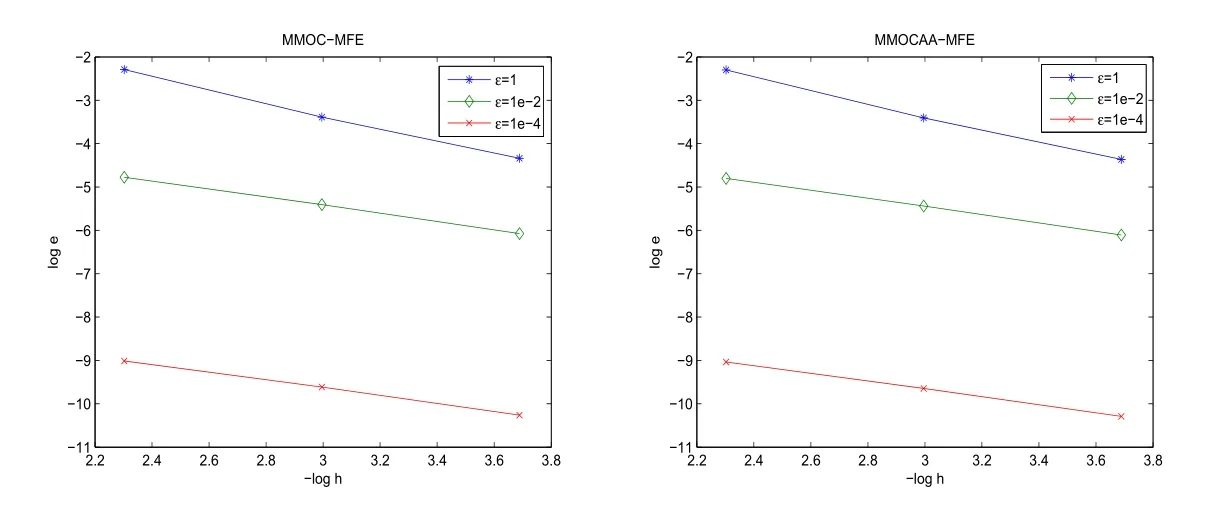
图1 b=[x2,−x1],Nt=N时的误差估计‖σ−σh‖L2.

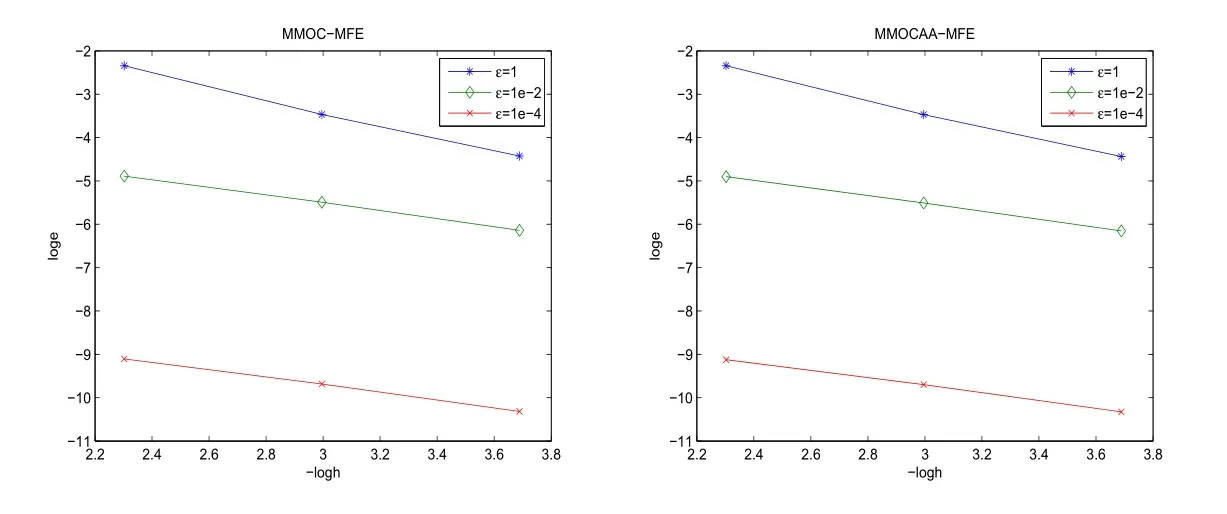
图2 b=[x2−x1,x2],Nt=N时的误差估计‖σ−σh‖L2.

§4 数值结果

在实际计算中,可以选取(??a)(或(??a))求解uh.(??a)(或者(??a))为经典的特征有限元算法,因此只需要给出数值结果去检验算法(??b)(或(??b))即可.考虑二维边值问题,并取Ω=[0,1]×[0,1],时间区间为(0,T]=(0,1].

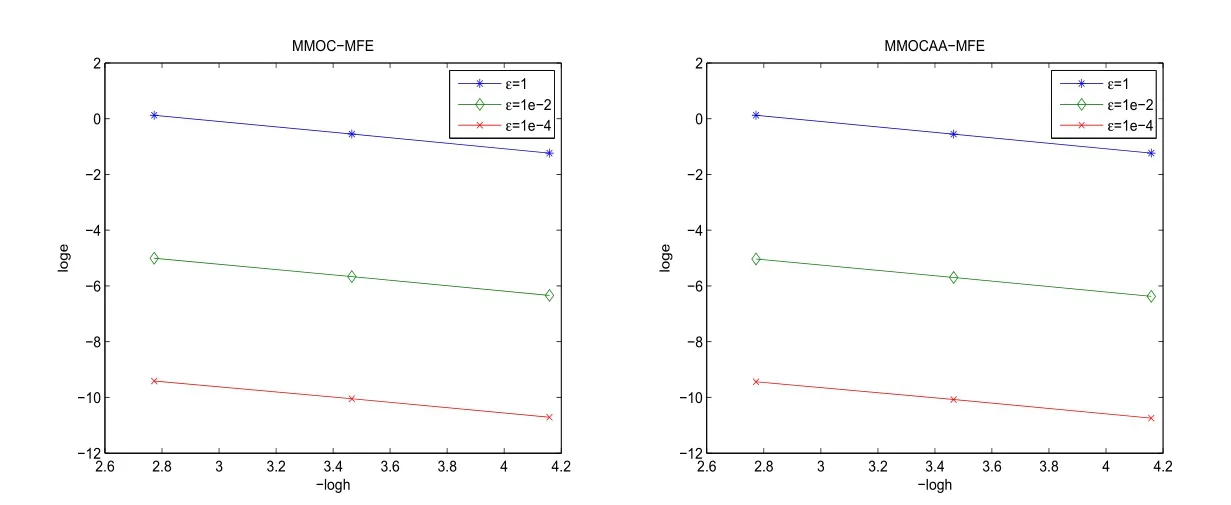
图3b=[x2,−x1],Nt=N时的误差估计|‖σ−σh‖|ˆL(0,T;H(div)).

在这个算例中初始边界条件由真解u=e−tsin2(πx1)sin2(πx2)给出.令σ= −ε∇u.首先将(0,T]分差Nt等份,△t=T/Nt.然后将区域Ω分成N×N一致矩形单元,令hu=hσ=1/N,再将每个矩形单元分成两个三角形单元从而获得一致三角网格剖分.基于此三角网格剖分选取分片线性多项式空间作为有限元空间.通过选取不同的网格参数以及对流项系数b和扩散系数ε,得到相应的收敛性估计,见图1,图2和图3.这些数值结果显示本文的算法是稳定的和收敛的.

致谢在此由衷地感谢各位评审老师,正是你们真挚的意见和建议,大大地提升了本文的质量.

[1] Douglas Jr J,Russell T F.Numerical methods for convection-dominated di ff usion problems based on combining the method of characteristics with fi nite element or fi nite di ff erence procedures[J].SIAM J Numer Anal,1982,19(5):871-885.

[2] Suli E.Convergence and nonlinear stability of the Lagrange-Galerkin method for the Navier-Stokes equations[J].Numer Math,1988,53(4):459-483.

[3] Pironneau O.On the transport-di ff usion algorithm,its application to the Navier-Stokes equations[J].Numer Math,1982,38(3):309-332.

[4] Pironneau O.Finite Element Methods for Fluids[M].John-Wiley Sons,Chichester,1989.

[5] Russell T F.Time stepping along characteristics with incomplete iteration for a Galerkin approximate of miscible displacement in porous media[J].SIAM J Numer Anal,1985,22(5):970-1013.

[6] 朱江.KdV方程的特征数值方法[J].高等学校计算数学学报,1988,10(1):11-27.

[7] 朱江.非线性RLW方程的特征数值方法[J].应用数学学报,1990,13(1):64-73.

[8] Pironneau O,Liou J,Tezduyar T.Characteristic-Galerkin and Galerkin/least-squares spacetime formulations for the advection-di ff usion equations with time dependent domains[J].Computer Methods Appl Mech Engrg,1993,27(3):205-227.

[9] Douglas Jr J,Furtado F,Pereira L F.On the numerical simulation of water fl ooding of heterogeneous petroleum reservoirs[J].Comput Geosciences,1997,1(2):155-190.

[10]Douglas Jr J,Huang Chieh-Sen,Pereira L F.The modi fi ed method of characteristics with adjusted advection[J].Numer Math,1999,83(3):353-369.

[11]Wang Kaixin,Wang Hong. A uniform estimate for the MMOC for two-dimensional advection-di ff usion equations[J].Numer Meth Part Di ff er Eq,2010,26(26):1054-1069.

[12]张建松,朱江,郭会,付红斐.对流扩散反应方程的特征分裂最小二乘方法[J].高等学校计算数学学报,2012,34(4):289-299.

[13]Zhang Jiansong,Yang Danping,Shen Shuqian,et al.A new MMOCAA-MFE method for compressible miscible displacement in porous media[J].Applied Numerical Mathematics,2014 80(3):65-80.

[14]Zhang Jiansong,Guo Hui.A split least-squares characteristic mixed element method for nonlinear nonstationary convection-di ff usion problem[J].International Journal of Computer Mathematics,2012,89(7):932-943.

[15]Arbogast T,Wheeler M F.A characteristics-mixed fi nite element method for advectiondominated transport problems[J].SIAM J Numer Anal,1995,32(2):404-424.

[16]Ewing R E,Russell T F,Wheeler M F.Convergence analysis of an approximation of miscible displacement in porous media by mixed fi nite elements and a modi fi ed method of characteristics[J].Computer Methods Appl Mech Engrg,1984,47(1-2):23-92.

[17]Ewing R E,Yuan Yirang,Li Gang.Time-stepping along characteristics for a mixed fi niteelement approximation for compressible fl ow of contamination from nuclear waste in porous media[J].SIAM J Numer Anal,1989,26(6):1513-1524.

[18]Yang Daoqi. A characteristic mixed method with dynamic fi nite element space for convection-dominated di ff usion problems[J].J Comput Appl Math,1992,43(3):343-353.

[19]Zhang Jiansong,Yang Danping.A splitting positive de fi nite mixed element method for second order hyperbolic equations[J].Numer Meth Part Di ff er Eqs,2009,25(3):622-636.

[20]Adams R A.Sobolev spaces[M].New York:Academic,1975.

[21]Ciarlet P G.The fi nite element methods for elliptic problems[M].New York:North-Holland,1978.

Split characteristic mixed fi nite element methods for advection-dominated di ff usion equation

ZHANG Jian-song1,ZHANG Yue-zhi1,ZHU Jiang2,YANG Dan-ping3
(1.Department of Applied Mathematics,China University of Petroleum,Qingdao 266580,China;2.Laborat´orio Nacional de Computa¸co Cient´ı fi ca,25651-075 Petr´opolis,RJ,Brazil;3.Department of Mathematics,East China Normal University,Shanghai 200062,China)

A split modi fi ed method of characteristics mixed fi nite element(SMMOC-MFE)and a split modi fi ed method of characteristics with adjusted advection mixed fi nite element(SMMOCAAMFE)are proposed for solving advection-dominated di ff usion equations,in which the mixed element systems are symmetric positive de fi nite,and the original variable u and the di ff usive fl ux σ = −ε∇u can be solved separately.The optimal-order error estimates in weighted energy norm are derived and some numerical implementations are given to con fi rm the convergence results.

advection-dominated di ff usion equations;mixed element;the method of characteristics;split solution;symmetric positive de fi nite system

65M25;65M60;65M12;65M15

O175.14

A

:1000-4424(2016)03-0338-13

2016-04-10

国家自然科学基金(11126084;11401588);山东省自然科学基金(ZR2014AQ005);中央高校基础研究专项基金(R1510063A)