具有无穷边界值的二次非线性奇摄动边值问题的双边界层

韩建邦,沈启霞

(郑州科技学院基础部,河南郑州450064)

具有无穷边界值的二次非线性奇摄动边值问题的双边界层

韩建邦,沈启霞

(郑州科技学院基础部,河南郑州450064)

研究了具有无穷边界值的二次非线性奇摄动边值问题的双边界层,利用边界层校正函数,构造其渐近解,并利用微分不等式理论,给出了一致有效渐近估计.最后给出算例验证了相关结论的正确性.

无穷大边界值:双边界层;边界层校正;微分不等式

§1 引 言

关于带Dirichlet、Robin等边界条件的二阶奇摄动边值问题的边界层,内层与角层现象等,利用微分不等式理论,Chang与Howes[1]已作了详细总结,Kevorkian及Cole[2]以几类具体的拟线性奇摄动边值问题为例,指出了二阶拟线性奇摄动边值问题解的渐近行为的复杂性.然而他们工作不涉及具有无穷边界值条件的奇摄动边值问题.近年来,具有无穷大边界值的奇摄动问题引起了学者的兴趣.倪明康[3]研究了拟线性方程组的无穷大初值问题,并对该问题的一致有效渐近解进行构造,对渐近解的余项进行估计.莫嘉琪等[4-7]基于双曲正、余切函数,研究了几类二阶拟线性奇摄动边值问题的激波解,对激波出现的条件与位置进行了讨论．王爱峰与倪明康[8]研究了如下问题:

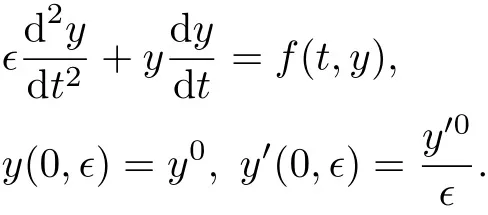
通过变换,将上述问题转化为吉洪诺夫系统,利用边界层函数法构造了问题形式渐近解,并利用逐次逼近法证明了解的存在唯一性,同时给出了渐近解的一致有效的估计.胡永生等[9]研究了如下具有无穷大边界值的半线性奇摄动Robin问题:

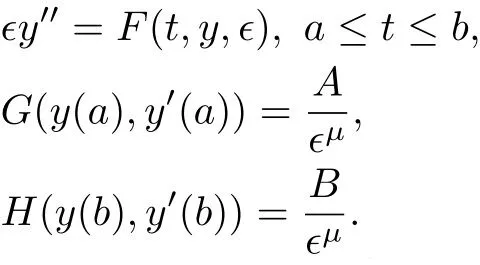
其中ϵ为正的小参数,h(t,y)为[a,b]×R上足够光滑的函数，pi＞0(i=1,2),A,B均为常数，并分析上述问题的双边界层行为.周哲彦等[10]研究了如下带有无穷大边界值的二阶拟线性奇摄动Robin问题：

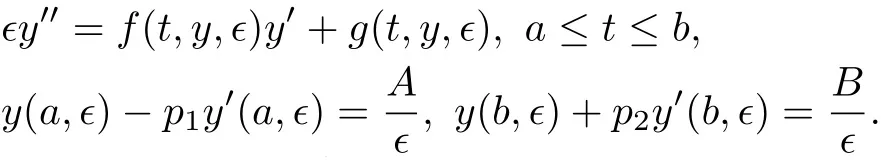
构造了边值问题在左、右两个端点领域的边界层校正函数,给出了问题的解关于退化解的渐近估计,而对于带无穷边界值的二次奇摄动问题的双边界层行为研究较少,如韩建邦等[11]考虑如下带无穷边界值的二次奇摄动Robin问题：

重点关注边界值的奇异程度对解的边界层行为的影响。基于此,主要针对如下具有无穷大边界值的二阶非线性奇摄动Robin问题：

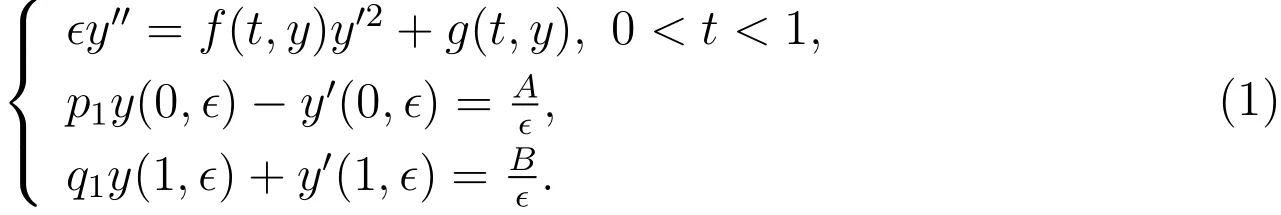
其中ϵ＞0为小参数,p1,q1≥0,A,B都为常数,y∈R为状态变量,本文研究问题(1)在两区间端点处的双边界层行为,并给出了问题的一致有效渐近估计,最后给出算例验证了相关结论的正确性.

§2 主要结论

问题(1)的退化方程如下：

假设其有某个解u=u(t)∈C2[0,1].

若在问题(1)中,边界值固定且满足A＞0,B＞0,则对于充分小的ϵ,总有

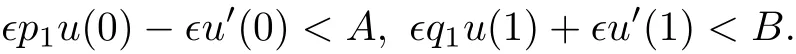
成立,此时定义区域:

其中d+(t)为正的连续函数,满足

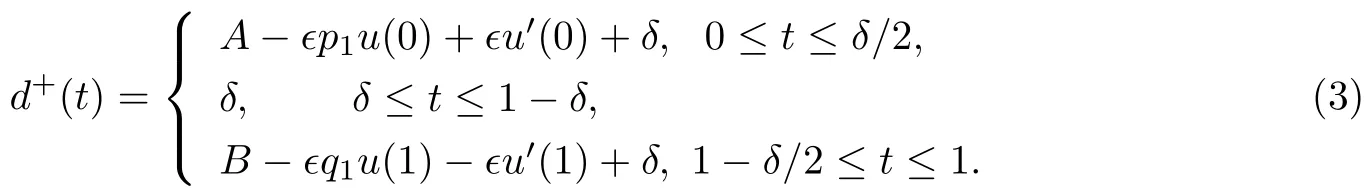
若A＜0,B＜0,则对于充分小的ϵ,总有

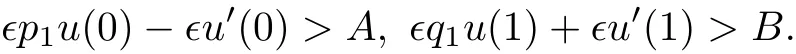
此时定义区域:

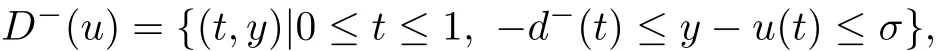
其中d−(t)为正的连续函数,满足

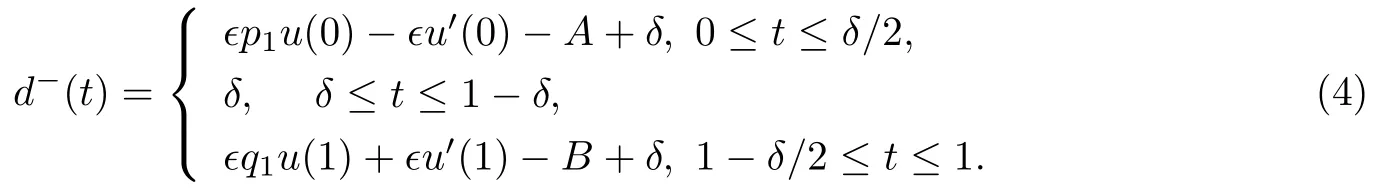
若A＞0,B＜0,则对于充分小的ϵ,总有

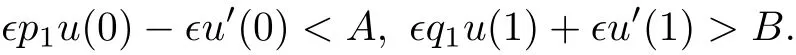
此时定义区域:

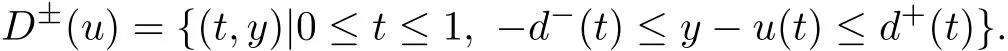
其中d+(t),d−(t)为正的连续函数,满足

若A＜0,B＞0,则对于充分小的ϵ,总有

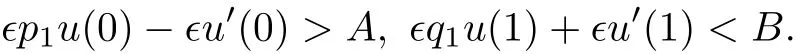
此时定义区域:

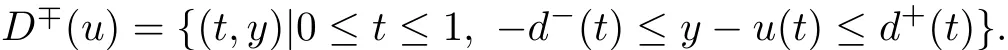
其中d+(t),d−(t)为正的连续函数,满足

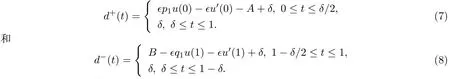
定义1令h(t,y)=f(t,y)u′2+g(t,y),称u=u(t)在[0,1]为Iq稳定的,如果存在常数m＞0,使得

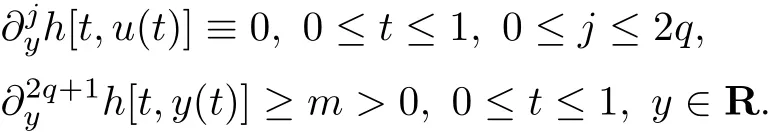
定义2退化方程(2)的解u=u(t)在[0,1]中是局部强(弱)稳定的,如果存在常数k＞0和小的常数σ ＞ 0,使得对于D(u)=D+(u)、D−(u)、D±(u)、D∓(u),如果 ϵp1u(0)− ϵu′(0)/=A,那么在 D(u)∩[0,σ]中

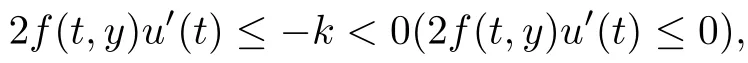
如果ϵq1u(1)+ ϵu′(1)/=B,那么在D(u)[1 − σ,1]中

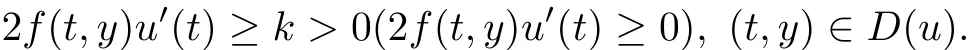
2.1 局部强稳定情形

定理1假设问题(2)具有局部强稳定的解u=u(t)∈C2[0,1]满足:存在某一正常数γ,使得

1)在D+(u)∩{[0,δ]∪[1− δ,1]}中f(t,y)≥ γ ＞ 0;

2)在D−(u)∩{[0,δ]∪[1− δ,1]}中f(t,y)≤ −γ ＜ 0;

3)在D±(u)∩[0,δ]中f(t,y)≥ γ ＞ 0 和在D±(u)∩[1− δ,1]中f(t,y)≤ −γ ＜ 0;

4)在D∓(u)∩[0,δ]中f(t,y)≤ −γ ＜ 0和在D∓(u)∩[1− δ,1]中f(t,y)≥ γ ＞ 0.

那么,存在ϵ0＞ 0,使得当 0＜ ϵ≤ ϵ0时,问题(1)在[0,1]中有解 y=y(t,ϵ)满足

函数wR(t,ϵ)满足

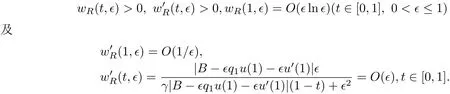
同理可以验证,wR(t,ϵ)是如下非线性边值问题的解:

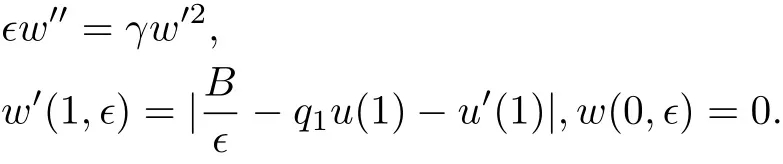
当ϵ充分小时,显然α(t,ϵ)≤ β(t,ϵ)且

进一步

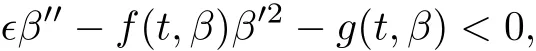
所以问题(1)在[0,1]中具有解y=y(t,ϵ)满足α(t,ϵ)≤ y(t,ϵ)≤ β(t,ϵ).

2.2 局部弱稳定情形

局部弱稳定是比局部强稳定弱的一种稳定性条件,在局部弱稳定条件之下,本文的方法无法直接处理奇摄动问题(1),必须降低边界值的奇异程度.为此,在(1)中令ϵ=µ2并考虑如下(边界值奇异性更低)的奇异摄动问题:

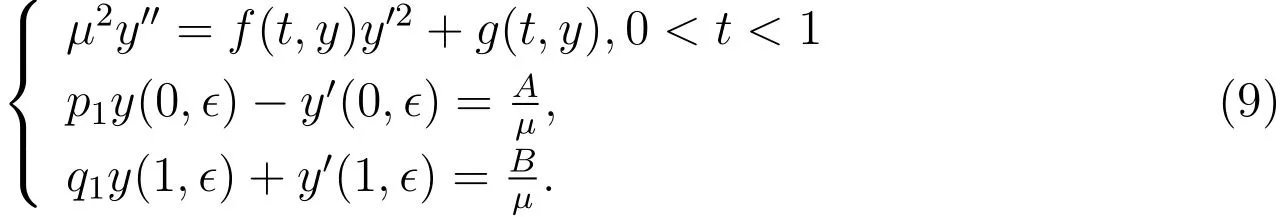
定理2假设退化方程(2)具有局部弱稳定且是 eq稳定的解u=u(t)∈C2[0,1],

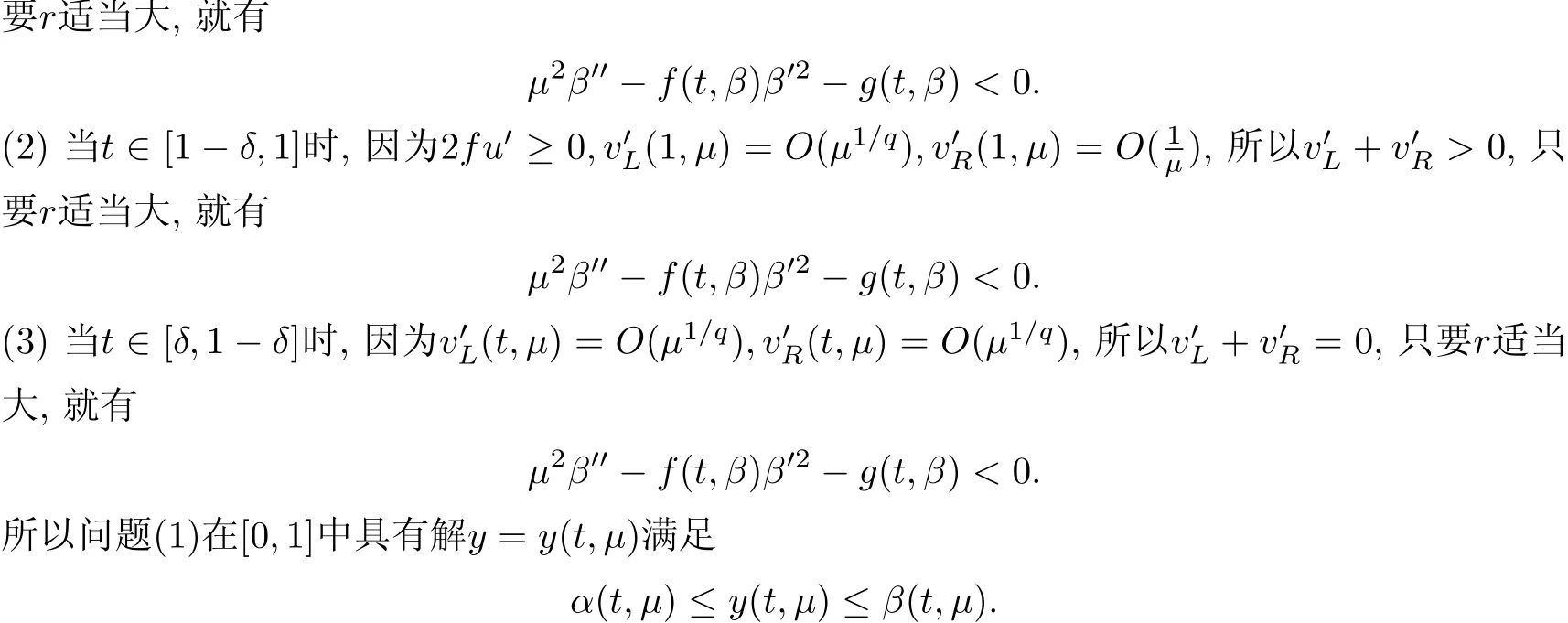
§3 算 例

当µ→0时,得

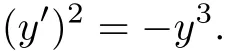
这与其退化方程(u′)2+u3=0一样,从而反应出当µ→0时,退化解趋近于精确解.

[1] 章国华,侯斯.非线性奇异摄动现象理论和应用[M].林宗池,译.福州:福建科学技术出版,1989.

[2] Kevorkian J,Cole J D.Perturbation methods in appliedmathematics,2nd ed[M].New York:Springer-Verlag.1985.

[3] 倪明康.临界情况下一类拟线性方程组的初值问题[J].华东师范大学学报(自然科学版),2006(1):15-16.

[4] Mo Jiaqi,Wang Hui. Shock solution for quasilinearsingularly perturbed Robin problem[J]．Progress in Natural Science,2002,12(12):945-947.

[5] 莫嘉琪,王辉,林万涛.一类二阶非线性方程的激波解[J].工程数学学报,2005,22(6):1109-1112.

[6] 莫嘉琪,林万涛.一类奇摄动非线性方程的激波解[J].系统科学与数学,2006,26(6):737-743.

[7] 莫嘉琪.一类拟线性方程Robin问题的激波解[J].数学物理学报,2008,28A(5):818-822.

[8] 王爱峰,倪明康.一类拟线性奇摄动方程的无穷大初值问题[J].吉林大学学报(理学版),2010,48(1):52-56.

[9] 胡永生,沈建和,周哲彦.一类带非线性无穷大边界值条件的二阶半线性方程奇摄动问题[J].应用数学学报,2013,36(2):306-314.

[10]周哲彦,沈建和.具有无穷大边界值的二阶拟线性奇摄动Robin问题的双边界层[J].福建师范大学学报(自然科学版),2011,27(4):7-13.

[11]韩建邦,沈建和,周哲彦.一类具有无穷边界值的二次奇摄动边值问题[J].高校应用数学学报,2013,28(2):180-188.

Double boundary layers of quadratic nonlinear singularly perturbed boundary value problem with in fi nite boundary values

HAN Jian-bang,SHEN Qi-xia
(Department of Basic Course,Zhengzhou University of Science and Technology,Zhengzhou 450064,China)

Double boundary layers of quadratic nonlinear singularly perturbed boundary value problem with in fi nite boundary values is studied.Using the boundary layer correction function,its asymptotic solution is constructed,and using the theory of di ff erential inequality,the uniformly valid asymptotic estimation is presented.Finally,an example is given to verify the validity of the relevant conclusions.

in fi nite boundary value;double boundary layers;boundary layer correction;di ff erential inequality

39A05;34B10

O175.14

A

:1000-4424(2016)03-0316-11

2016-01-07

2016-07-24

河南省科技厅基础与前沿技术研究计划(132300410360)