Gamma算子在Orlicz空间L∗Φ(0,∞)中加Jacobi权同时逼近的强逆不等式

韩领兄,吴嘎日迪

(1.内蒙古民族大学数学学院,通辽028043;2.内蒙古师范大学数学科学学院,呼和浩特010022)

Gamma算子在Orlicz空间L∗Φ(0,∞)中加Jacobi权同时逼近的强逆不等式

韩领兄1,吴嘎日迪2

(1.内蒙古民族大学数学学院,通辽028043;2.内蒙古师范大学数学科学学院,呼和浩特010022)

讨论由Young函数生成的Orlicz空间的性质, 并给出Orlicz空间具有Hardy-Littlewood性质的充要条件,然后借助加Jacobi权修正的K-泛函和加Jacobi权连续模及其等价性建立Gamma算子在Orlicz空间中加权同时逼近的两种强逆不等式.

Orlicz空间;Young函数;Gamma算子;K-泛函

§1 引言及主要定理

近年来人们对Orlicz空间感兴趣,因为Lp空间提供的活动天地和度量标准只适合于处理线性的和充其量是多项式型的非线性问题.随着越来越多的非线性问题的出现(见[1]),从Lp空间过渡到Orlicz空间已成为历史的必然,这正是研究Orlicz空间的意义所在.下面介绍Orlicz空间(见[2]).

定义1.1设Φ(t)为定义在区间(0,∞)上的凸连续函数,若Φ(t)满足

则称Φ(t)为Young函数.

Young函数Φ(t)的互余Young函数记为Ψ(t).

由Young函数Φ(t)的凸性得到

定义1.2设Φ(t)为Young函数.若存在常数t0＞0和C≥1,使得当t≥t0时,有

则称Young函数Φ(t)满足∆2-条件(记为Φ ∈ ∆2).

推论1.1Φ∈∆2当且仅当对于任意的b＞1,存在两个正数α,C,使得当t≥t0时

定义1.3设Φ(t)为Young函数.Orlicz类LΦ(0,∞)为使有限积分

存在的在区间(0,∞)上可测的函数u(x)的全体.Orlicz空间为赋予Luxemburg范数

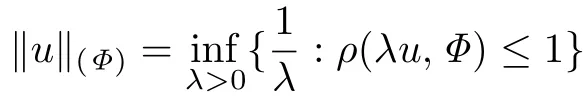
的Orlicz类LΦ(0,∞)的线性包.有如下性质:

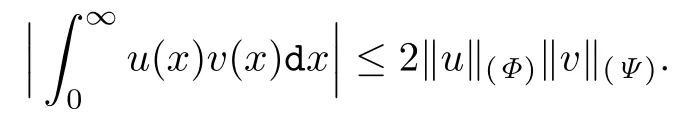
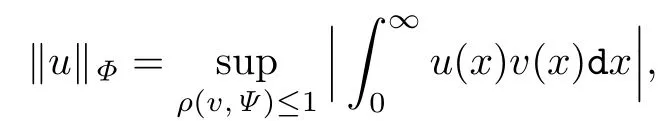
它与Luxemburg范数等价,即

设f(x)为(0,∞)上的可积函数,Gamma算子Gn[3]的定义如下

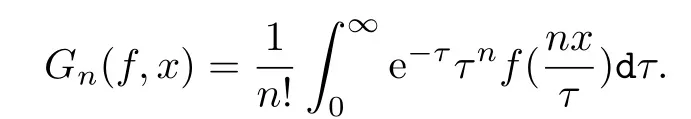
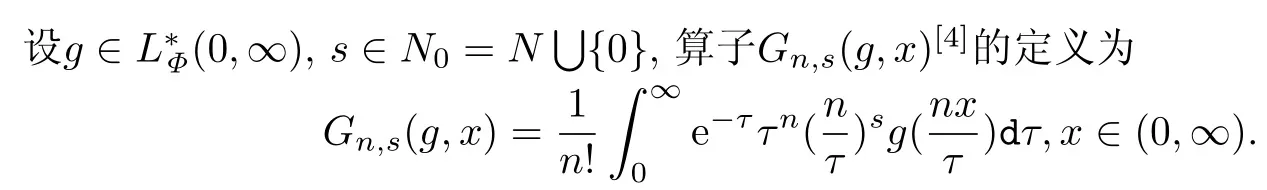
应用加权Ditizian-Totik模对正线性算子在Lp(1≤p≤∞)范数下的正定理和逆定理,已有广泛的研究[3,5-7].为了对逼近性质有更细致的刻划,人们进一步研究了各种形式的强逆不等式[4,8-13].Totik在文[13]中给出了L∞范数下的B-型强逆不等式的证明方法.Chen与Dizian[10]给出了Lp(1＜p≤∞)空间中Bernstein-Kantorovich多项式的B-型强逆不等式.有关A-型强逆不等式的证明方法和结果见文献[7,9,11-12].

Gamma算子是一类重要的正线性算子,它广泛应用于概率论及计算数学中,对于Gamma算子的性质及逼近定理已有深刻的研究[3,5-6].Adell[8]研究了非中心的Gamma算子在确界范数下的A-型强逆不等式.文[4]在Lp(1≤p≤∞)空间中证明了Gamma算子同时逼近的强逆不等式.在文[14]中得到关于Gamma算子在空间中同时逼近的如下强逆不等式:

定理A设f∈n＞1,Ψ∈∆2,φ(x)=x,则存在常数K ＞1,当l≥Kn时,有

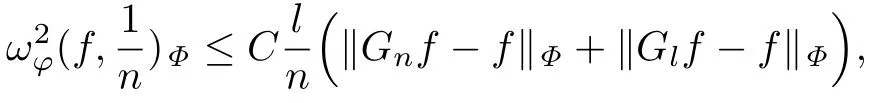
其中C是与n 和x无关的正常数.

本文中常数C在不同的地方取值也许不同.

定理1.1设wf(s)∈,s∈N,n＞s+1,a≥s−2,a+b≥s−2,Ψ ∈ ∆2,则存在常数K＞1,当l≥Kn时,有

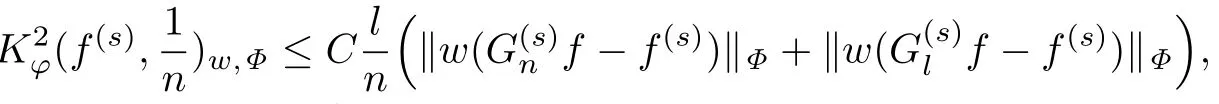
其中φ(x)=x,w(x)=xa(1+x)b.

注1.1关于定理A和定理1.1中结果的意义,如l≥Kn,这是定理的条件,加这一条件的目的是出于证明过程的需要,逼近论中这类结果叫逆定理.

推论1.2在定理1.1的条件下,当s＜α＜s+2,时有

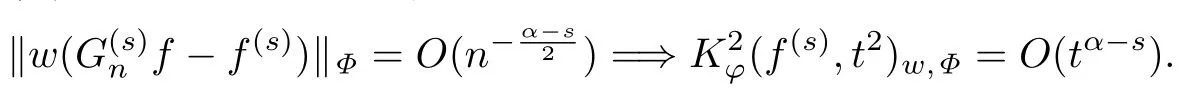
定理1.2设wf∈n＞ 1,a≥ 0,a+b≥ −2,Ψ ∈ ∆2,则存在常数K ＞ 1,当l≥ Kn时,有

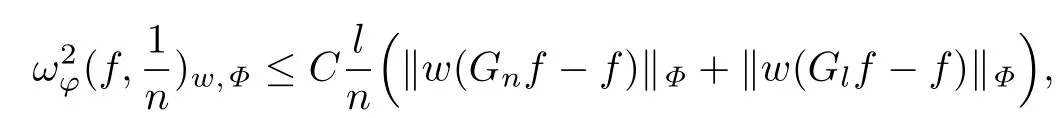
其中φ(x)=x,w(x)=xa(1+x)b.

注1.2定理A是定理1.2当w(x)=1时特殊情况.

§2 Orlicz空间(0,∞)的Hardy-Littlewood性质

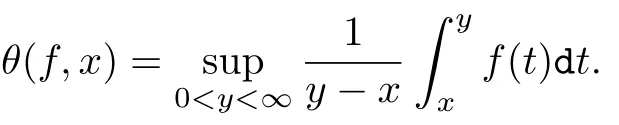
众所周知,Hardy-Littlewood函数在逼近论中有非常重要作用.Lp(D)空间和由N函数M(u)生成的有限区间上的Orlicz空间具有Hardy-Littlewood性质.本节给出了Orlicz空间具有Hardy-Littlewood性质的充要条件.

显然,对于正递减函数f(x)的Hardy-Littlewood函数θ(f,x)等价于函数

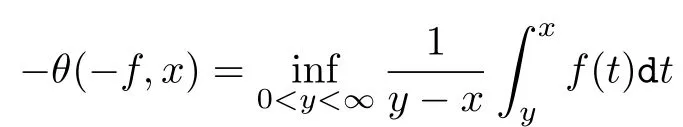
之间,因而HLP蕴含HLP′且蕴含HLP′′.

性质2.1Orlicz空间的三个性质HLP,HLP′和HLP′′等价且分别有

其中C为常数.

证由[15]得到Orlicz空间是重排不变的.对于函数f∈设f∗为函数|f|的递减的重排,则Orlicz空间有性质HLP′′时f∗∈.从而由[16](420-421页),当x ＞ 0时,有

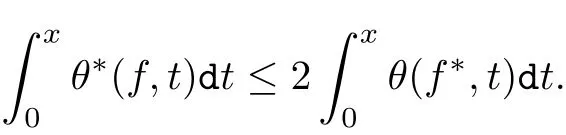
因此

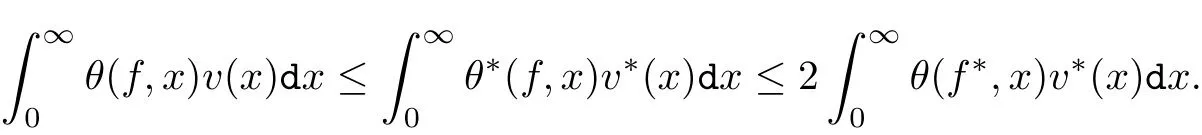
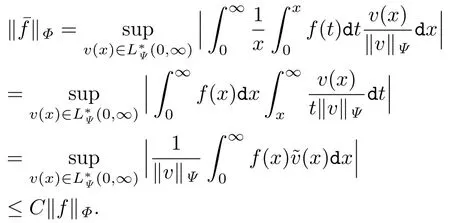
假设Ψ不满足∆2条件,则由定义1.2,对任意C≥1和t0＞0,存在b≥t0,使得

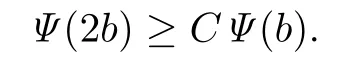
对于任意的0＜u＜∞都有Ψ(u)有限的,所以必存在一列bk→∞,使得

由性质2.1和性质2.2直接推得下面的定理.

定理2.1设Ψ ∈ ∆2,则存在常数C,使得

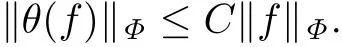
注2.1性质2.1和2.2在Lp空间中有对应结果,可见参考文献[15].

§3 定理1.1的证明

成立,所以由(3.1)式,有

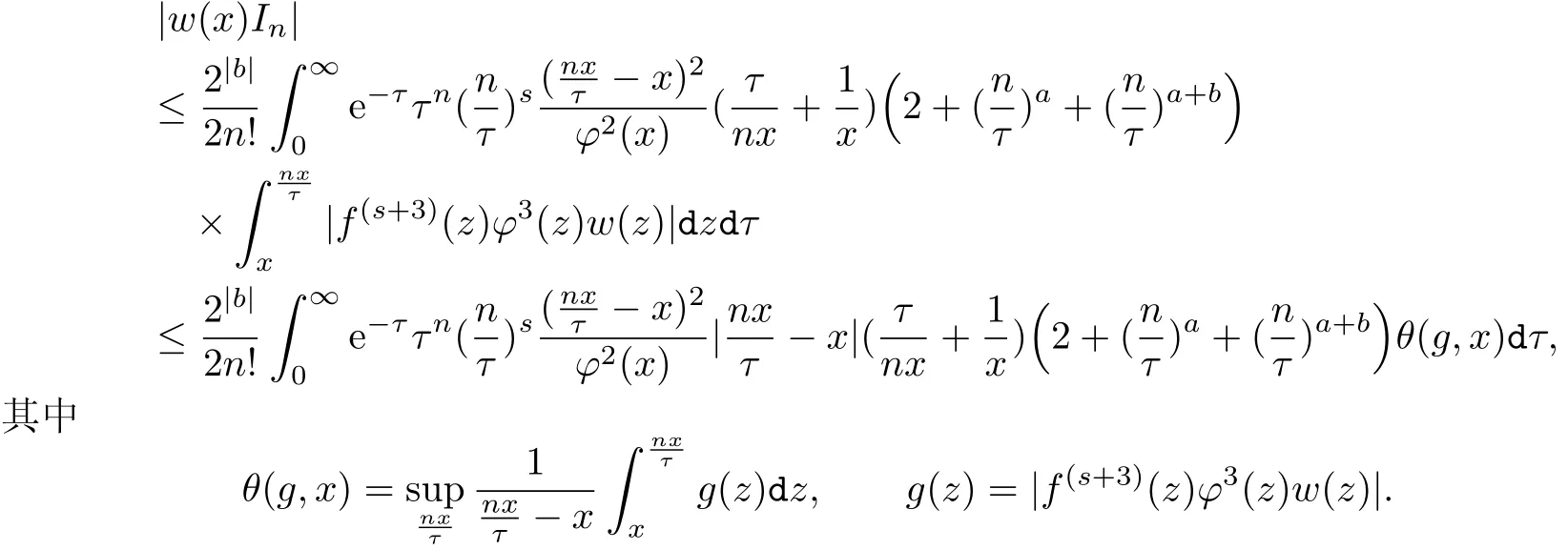
运用定理2.1和引理3.1,得到

再由(3.6)式就能完成定理1.1的证明.

§4 定理1.2的证明

设权函数φ(x),x∈(0,∞)满足以下条件(见[3]):

(1)局部φ～ 1,即对于每个子区间[a,b]⊂(0,∞),存在常数M ≡M(a,b)＞0,使得当x∈[a,b]时,M−1≤ φ(x)≤ M.

(2)设β(0)和β(∞)为两个常数且β(0)≥ 0,β(∞)≤ 1,满足

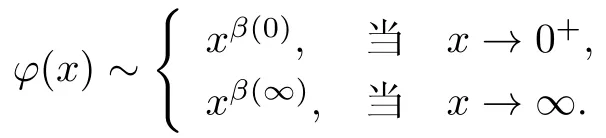
(3)φ(x)在R上L可测且存在两个常数M0和h0,使得对于0＜h≤h0和每个有限区间E⊂(0,∞)有,

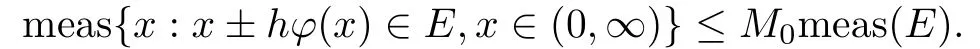
常用的权函数φ有

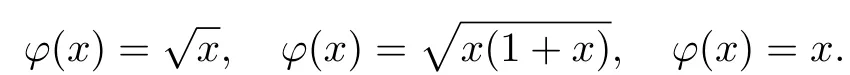
Jacobi权函数w(x)=xa(1+x)b在(0,∞)上L可测且当0 ≤ β(0)＜ 1时,设a ≥ 0.

加Jacobi权K-泛函定义为

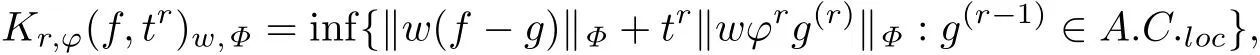
其中w为Jacobi权函数,φ为权函数.

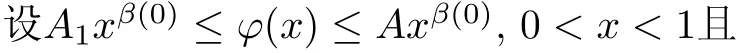
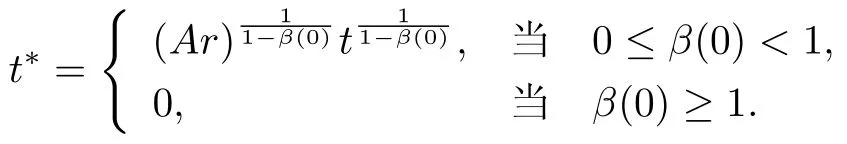
加Jacobi权连续模定义为:

当a=0或β(0)≥ 1时,

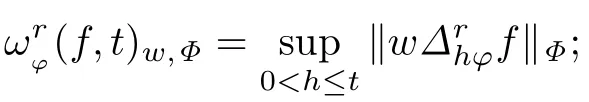
当a＞0且0≤ β(0)＜ 1时,

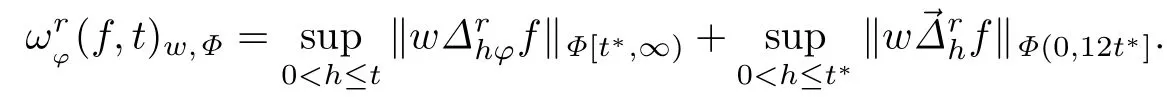
下面给出加Jacobi权连续模与加Jacobi权K-泛函的等价性定理:

定理4.1设则存在常数C和t0使得,当0＜t≤t0时,有

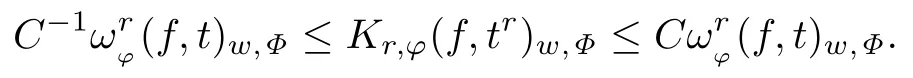
注4.1定理4.1在Lp空间中也有相应结果,可见参考文献[3].

注4.2定理1[14]为定理4.1中w(x)=1时的特殊情形.

证第一种情况:当β(0)≥1时,因此w(u)～ w(x),φ(u)～ φ(x).K-泛函上界估计的证明和定理1[14],当β(0)≥ 1,β(∞)≤1时上界估计的证明方法相同;K-泛函下界估计的证明和定理1[14]的下界估计的证明方法相同.所以在此省略.

第二种情况:a=0,β(∞)可以不等于0.当x＜1时由定理1[14]的方法可以证明;当x＞1时,u同上,即w(u)～w(x),φ(u)～φ(x),这时由定理1[14]的方法可以证明.

第三种情况:a＞0且0≤β=β(0)＜1.这时把定理1[14]中的Gt(x)修改如下:把Gt,2(x)[14]和[14]分别替换为

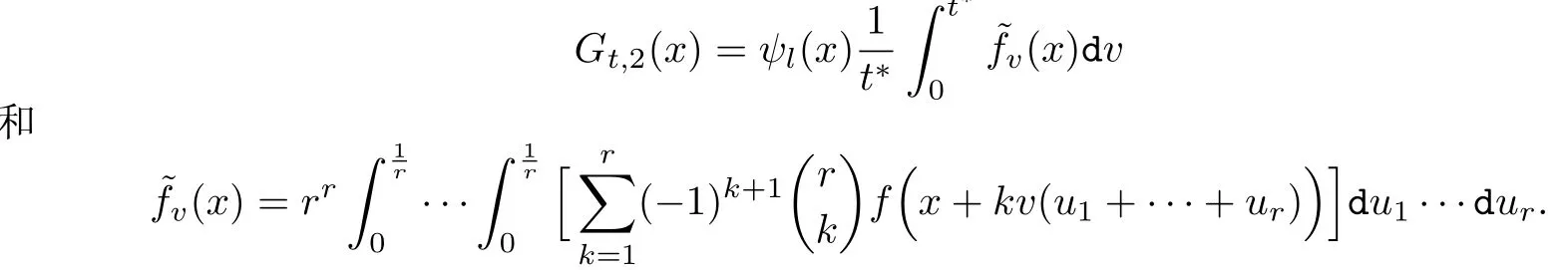
与定理1[14]的证明方法类似,可以得到

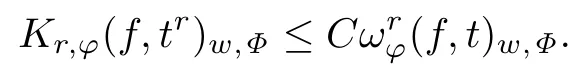
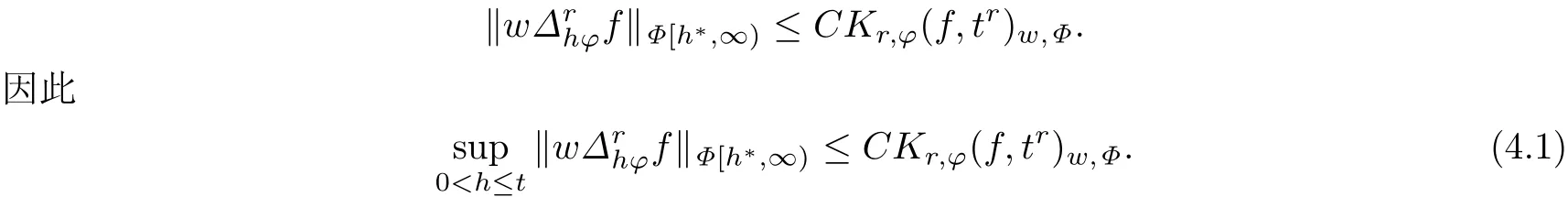
参考文献:

[1] 汪和平.Orlicz空间上的多项式逼近[D].北京师范大学,1993.

[2] He Yuzan.Ba spaces and Orlicz space[J].Function Spaces and Complex Analysis,Joensuu,1999,37-62.

[3] Ditzian Z,Totik V.Moduli of smoothness[M].New York:Springer-Verlag,1987.

[4] 齐秋兰,郭顺生,黄苏霞.Gamma算子在Lp(1≤p≤∞)空间带权同时逼近的强逆不等式[J].数学物理学报,2008,28A(3):537-545.

[5] Guo Shunsheng,Qi Qiulan.Pointwise weighted simultaneous approximation by Gamma operators[J].J Nanjing University Mathematical Biquarterly,2003,20(1):24-37.

[6] Totik V.The Gamma operators in Lpspaces[J].Publ Math,1985,32:43-55.

[7] Totik V.Approximation by Bernstein polynomials[J].Amer J Math,1994,116:995-1018.

[8] Adell J.A strong converse inequality for Gamma-type operators[J].Constr Approx,1999,15:537-551.

[9] Chen Wen.Strong converse inequality for the F operators[J].Analysis,1994,14:267-279.

[10]Chen Wen,Ditzian Z.Strong converse inequality for Kantorovich polynomials[J].Constr Approx,1994,10:95-106.

[11]Ditzian Z,Ivanov K G.Strong converse inequalities[J].J Anal Math,1993,61:61-111.

[12]Gonska H H,Zhou X L.The strong converse inequalities for Bernstein-Kantorovich operators[J].Comput Math Appl,1995,30:103-128.

[13]Totik V.Strong converse inequalities[J].J Approx Theory,1994,76:369-375.

[14]韩领兄,吴嘎日迪,刘国锋.Orlicz空间中加权光滑模与K-泛函的等价性及其应用[J].数学物理学报,2014,34A(1):95-108.

[15]Lorentz G G.Majorants in spaces of integrable functions[J].American Journal of Mathematics,1955,77(3):484-492.

[16]Lorentz G G.On the theory of spaces Λ[J].Paci fi c journal of Mathematics,1951,1:411-429.

Strong converse inequality of Jacobi weighted simultaneous approximation for Gamma operators in Orlicz spaces L∗Φ(0,∞)

HAN Ling-xiong1,WU Ga-ri-di2
(1.College of Mathematics,Inner Mongolia University for the Nationalities,Tongliao 028043,China;2.College of Mathematics Science,Inner Mongolia Normal University,Hohhot 010022,China)

The properties of Orlicz spacescorresponding to the Young function Φ(x)are discussed and the Hardy-Littlewood property of the Orlicz spacesis given.Then two kinds of strong converse inequalities of Jacobi weighted simultaneous approximation for Gamma operators are established by modi fi ed Jacobi weighted K-functional and Jacobi weighted modulus of smoothness in Orlicz spaces

Orlicz Space;Young function;Gamma operators;strong converse inequality

41A17;41A25

O174.41

A

:1000-4424(2016)03-0366-13

2015-06-30

2016-02-27

国家自然科学基金(11161033;11461052);内蒙古自治区自然科学基金(2014MS0107);内蒙古民族大学科学研究项目(NMDYB15087)