方差分保费原则下相依多险种模型的最优再保险

张节松, 肖庆宪

(1.上海理工大学管理学院,上海200093;2.淮北师范大学管理学院,安徽淮北235000)

方差分保费原则下相依多险种模型的最优再保险

张节松1,2, 肖庆宪1

(1.上海理工大学管理学院,上海200093;2.淮北师范大学管理学院,安徽淮北235000)

采用共同冲击型相依多险种模型刻画保险公司的索赔风险过程,按照方差分保费原则计算再保险费,研究最小化破产概率的再保险问题.通过扩散逼近并利用动态规划原理,得到了显式最优策略和值函数.与采用期望值分保费原则比较,发现最优分保形式和自留风险水平均不相同;与最大化期望指数效用的结果比较,发现最优分保比例除了与安全负载相关,还与索赔分布、计数过程以及直接保险费收入率c有关.最后,结合数值算例揭示了相依参数的动态影响以及最优策略与c的敏感相关性.

方差分保费原则;相依多险种模型;最优再保险;破产概率

§1 引 言

近年来,地震,台风,泥石流,火灾,工厂爆炸等自然灾害和公共安全类事件频发,政府和保险业对巨额损失保险问题越来越重视.再保险是防范和化解巨额风险的重要手段,合理安排再保险不仅能提高保险公司的偿付能力,维护可持续发展,也可以减轻政府财政救助负担,保障经济损失.不过,和直接保险一样保险人须要向再保险人支付分保费,且相对而言更为昂贵,原保险公司的收益会缩减.因此,保险人需要在风险与收益间进行平衡并尽可能作出最为合理的决策.实际上,最优再保险策略一直是精算学主要研究内容之一.Schmidli[1],Hipp&Taksar[2],Cao&Zeng[3]和张茂军等[4]考虑了最小化破产概率的最优再保险问题;Kaluszka[5]讨论了最小化自留风险方差的最优再保险安排;Cai et al.[6],Chi[7]以最小化尾部风险测度为优化目标,探讨最优再保险形式与自留额;Bai&Guo[8]和林祥&李艳方[9]采用最大化终期财富期望效用的优化准则,研究了最优投资-再保险策略;Hald&Schmidli[10]和Liang&Guo[11]则着眼于最大化调节系数,求解最优自留风险水平.值得说明的是,在上述优化准则中,最小化破产概率是一种内在的客观标准,与最大化期望效用等优化准则不同,它不取决于任何特殊个体的效用偏好,且现实意义非常直观.但同时,如果是在跳跃风险过程框架下,即便是经典的复合Poisson过程,一般也很难得到最优解的显式表达式.因此,常采用扩散逼近的方法将跳跃风险过程近似处理为漂移布朗运动[1-3].

上述最优再保险研究从宏观的角度将索赔风险刻画为单个随机变量或传统的复合Poisson过程亦或扩散逼近变形,主要适用于经营同质风险的保险企业.在现代保险实务中,尤其是在巨灾情形下,由于保险公司经营业务的不断多元化,一次事故往往会触发多险种的同时索赔且呈现出相依关系.例如,一次地震可能导致医疗保险,死亡保险,房屋保险,汽车保险等险种的共同索赔,且索赔强度均与此次地震的破坏性相关.因此,有必要采用相依多险种模型刻画保险公司的索赔风险.然而,截至目前,还只有少量最优再保险研究是在相依多险种模型框架下进行的.Centeno[12]在最大化期望指数效用和调节系数的优化标准下研究了相依双险种模型超额赔款再保险的最优自留限额.针对同一模型风险,Bai et al.[13]通过扩散逼近,在期望值保费原则下研究了最小化破产概率的最优再保险形式及其自留额;Liang&Yuen[14]则在方差保费原则和最大化终期财富期望指数效用的优化准则下,分别研究了跳跃模型和扩散逼近模型的最优比例再保险.鉴于Liang&Yuen[14]所得结果表明,在扩散逼近情形下两险种的最优自留风险水平相同且与索赔额分布及计数过程无关,Yuen et al.[15]采用相同的优化准则,但将相依双险种模型推广到更贴近保险实际的相依m(≥2)险种情形,并采用期望值分保费原则分别给出了跳跃情形和扩散逼近情形下的最优结果.

期望值原则和方差原则都是保费计算过程中所通常采用的方式.在期望值保费原则下,根据Bai et al.[13]命题2.1,超额赔款再保险是最小化破产概率的最优分保形式.该结论在方差保费原则下未必成立,因为根据Hipp&Taksar[2]命题7,此时的最优分保形式应为比例再保险.鉴于这一事实并受前述[13-15]等工作的启发,本文采用Yuen et al.[15]所述相依m(≥2)险种模型,以最小化破产概率为优化准则,在方差分保费原则下研究最优再保险问题.通过扩散逼近并运用动态规划原理,得到了最优自留风险水平及最小破产概率的解析表达式.同时,结合数值算例分析了相依参数和保费收入率的动态影响.结果表明,与Liang&Yuen[14]在期望指数效用最大化准则下所得的最优策略不同,最小化破产概率的最优策略不仅与安全负载有关,还与索赔分布,计数过程以及直接保险费收入率相关.特别的,与各险种间的相依参数相关,随着相依参数的增大,最优自留风险水平也增大.这与Bai et al.[13]同样为最小化破产概率,但采用期望值保费原则所得的结论也不相同,因为那里的数值分析表明最优自留限额是随着相依参数的增大而先减后增的.

§2 最优再保险模型

设保险公司经营m(≥2)种保险业务,如汽车保险,意外伤害险,医疗保险,寿险等.对第l(l=1,2,···,m)类经济业务,令(i=1,2,···)表示索赔序列,具有共同的分布函数Fl(x),满足x≤0时Fl(x)=0而x＞0时0＜Fl(x)＜1.由此,第l类保险业务的累积索赔过程可表示为

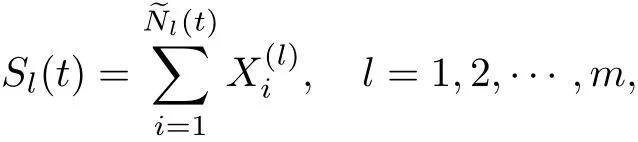
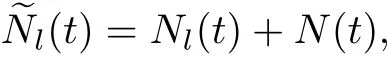
其中Nl(t)和N(t)为m+1个相互独立的Poisson过程,强度分别为λ1,λ2,···,λm和λ. 即m类保险业务同时受计数过程N(t)的冲击而相依.于是,所有m类保险业务的累积索赔过程可表示为

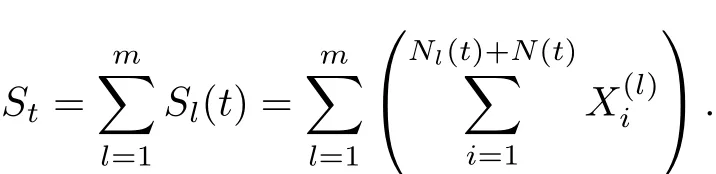
据此,定义保险公司的盈余过程为

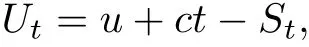
其中u为初始盈余,c为保险费收入率.

为保障巨额损失,保险公司对业务l安排t时刻自留风险水平为flt的再保险策略,如下部分由再保险公司承担.对flt,按照常规,约定0≤flt(x)≤x且在(0,∞)上单调递增,l=1,2,···,m.设分保费按照方差保费原则计算,安全负载为θ＞0,则原保险公司t时刻的净保费收入率为

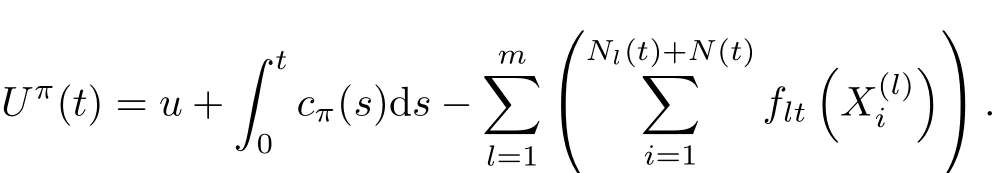
注1对于直接保险,仅假定保险费率为常数c,而未限定计算原理.但根据安全负载条件,应满足c＞E[St],否则保险公司必然以概率1破产.同时,再保险一般更为昂贵,也就是要求c＜E[St]+θvar[St],否则保险公司可以安排全额再保险,不承担任何风险而获得收益.

对任意给定再保险策略π,记τπ为盈余过程Uπ(t)关于0的首中时,也就是

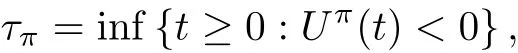
则破产概率定义为

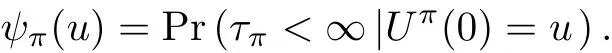
本文的目标就是要通过选择再保险策略π以使得破产概率最小,即求解最优策略π∗=使得

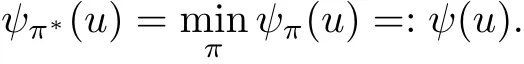
在相依多险种跳跃风险过程St框架下,破产概率ψπ(u)的显式表达式一般无法获得,所以要获得最小化破产概率的精确再保险策略是非常困难的.为使问题可处理并获得显式解,采用扩散逼近形式.

记分布函数Fl(x)对应的一阶矩和二阶矩分别为类似 Yuen et al.[15]的讨论知,在再保险策略π的安排下,保险公司实际盈余过程Uπ(t)的扩散逼近为

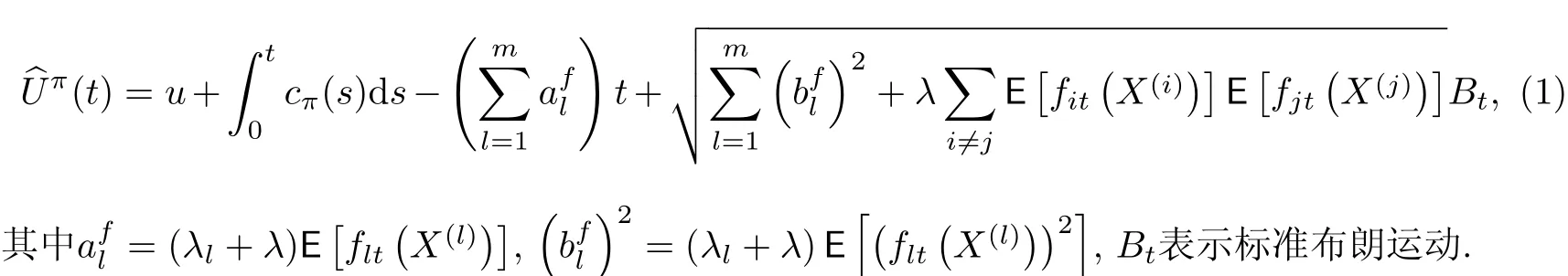
§3 最优再保险策略

由于采用的是方差分保费原则,根据Hipp&Taksar[2]命题7,此时的最优再保险形式应为比例再保险.下面求解各业务的最优自留风险比例.

假设在t时刻对业务l安排再保险比例1−ql(t),即自留风险比例为ql(t),0≤ql(t)≤1,l=1,2,···,m.在式(1)中令flt(x)=ql(t)x,l=1,2,···,m,则再保险策略(q1(t),q2(t),···,qm(t))下的盈余过程bUπ(t)满足随机微分方程

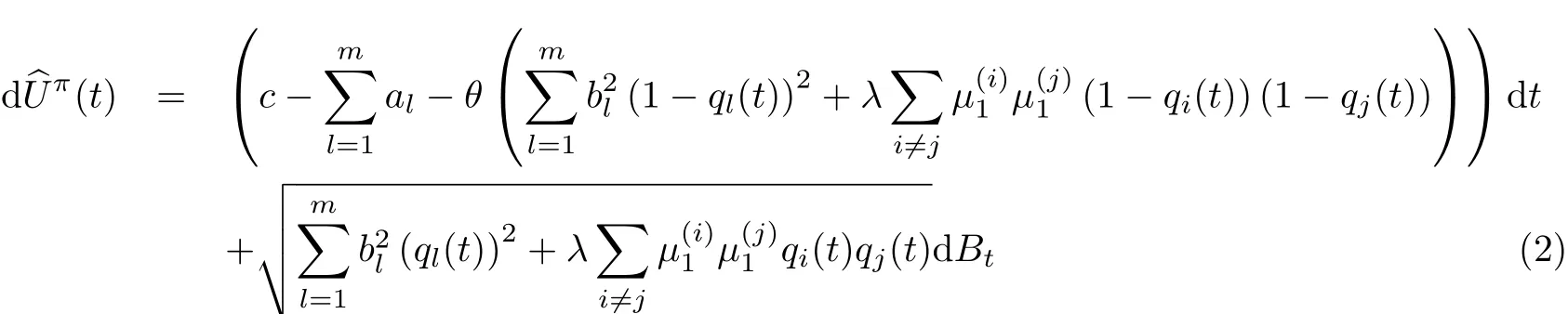
为解决上述问题,利用动态规划方法[16,13].通过标准论证可知,如果值函数ψ(u)在(0,∞)上二次连续可微,则ψ(u)满足HJB方程

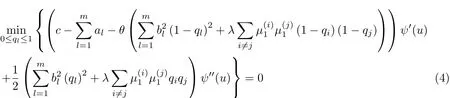
和边界条件

进一步,利用 Fleming&Soner[16](第Ⅳ.5部分)的一般方法,可得如下验证定理,说明由HJB方程(4)的二次连续可微解即可得到优化问题(3)的解.

定理3.1设v(u)为上述HJB方程(4)的解且二次连续可微,则ψ(u)即为v(u).并且,如果对所有的u＞0,

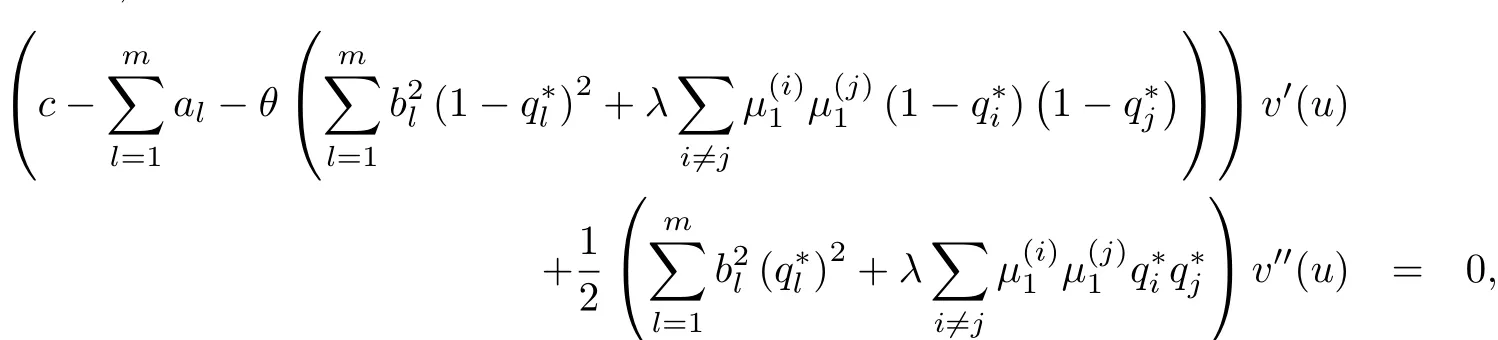
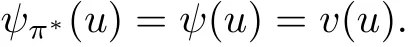
根据验证定理3.1,如果能找到满足HJB方程(4)的一个二次连续可微解v,也就得到了值函数ψ.为此,设v(u)为二次连续可微的凸函数且满足v′(u)＜0,同时定义

则方程组(7)又可表示为矩阵形式

其中T表示转置.

由Yuen et al.[15]引理4.1的证明知A正定,所以可逆.因此,解得

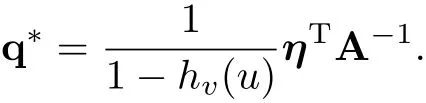
进一步,计算gv(q1,q2,···,qm)的二阶偏导数,有

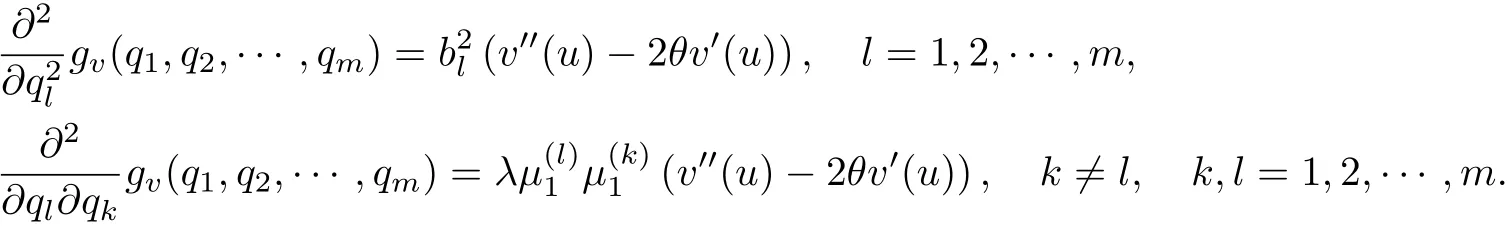
由此,可得Hessian矩阵

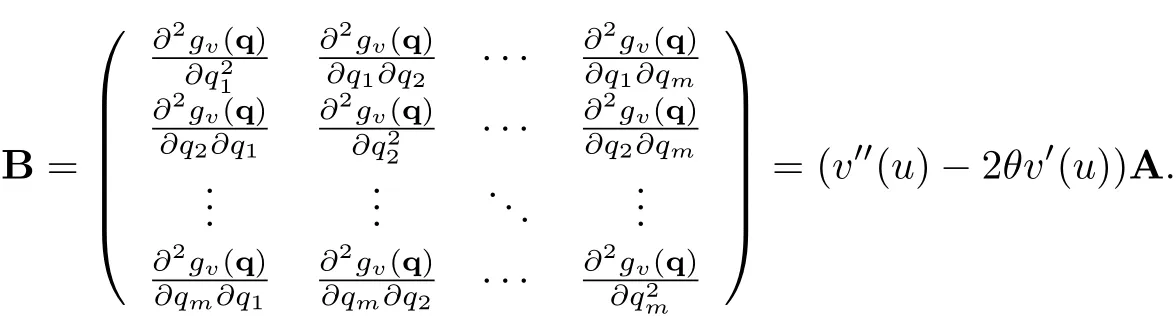
因为v′′(u)−2θv′(u)＞0,所以Hessian矩阵B在点也是正定的.因此,q∗必然为gv(q1,q2,···,qm) 的最小值点.

注意到AI= η,其中IT=(1,1,···,1)1×m,所以ηTA−1=IT.将此代入方程组(8),有

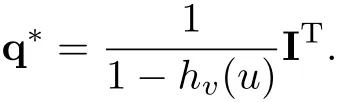
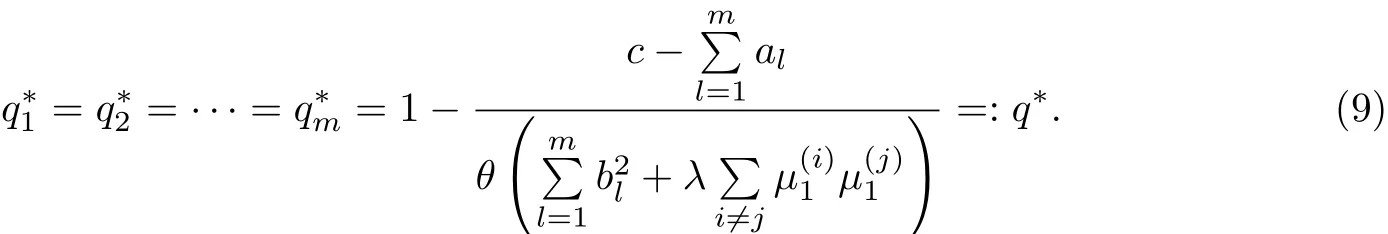
由注1易知q∗∈ (0,1),所以由验证定理3.1知π∗=(q∗,q∗,···,q∗)即为最优再保险策略.

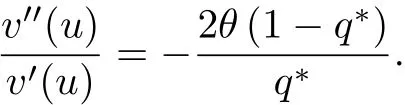
据此微分方程以及边界条件(5),不难解得

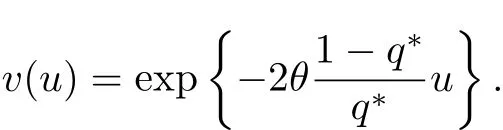
易见v(u)为二次连续可微的凸函数且满足v′(u)＜0.于是,由验证定理3.1知值函数ψ(u)=v(u).

最后,为总结上述讨论,给出如下定理.

定理3.2优化问题(3)的值函数为

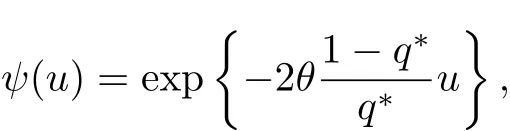
最优策略为π∗=(q∗,q∗,···,q∗),其中q∗由式(9)确定.

注2定理3.2是在最小化破产概率的优化准则下得到的,与最大化期望指数效用准则下的最优策略(见Liang&Yuen[14]定理4.1和 Yuen et al.[15]式(6.3))比较,发现既有共同之处,也存在明显的差异.首先,m类业务的再保险策略相等,这一点是共同的.不同的是,后者的最优策略相对简单,与直接保险的保费收入率、索赔分布以及计数过程诸因素无关,而由式(9)可知,前者的最优策略相对复杂,并且与上述因素均相关.可见,最小化破产概率是一种非常内在的客观标准,所得结果更符合保险实际.

§4 示例分析

本部分根据定理3.2具体示例,给出数值结果并分析相依参数λ和直接保险费收入率c对最优策略和值函数的动态影响.

假定保险公司拥有初始储备金u=4,经营两种类型的保险业务.业务1的索赔额变量X(1)服从参数为2的指数分布,业务2的索赔额变量X(2)服从参数为(1,3)的Gamma分布.设定λ1=3,λ2=4,直接保险费按照期望值原则收取,安全负载为0.15,再保险费按照方差原则计算,安全负载0.4.固定上述参数,下面分析参数λ和c的动态影响.

首先,设相依参数λ∈[0,3],得最优自留风险风险水平q∗关于λ的变化趋势如图1所示,最小破产概率ψ(u)如图2所示.然后,固定λ=1并根据注1限定c∈(3.67,5.04),可得最优策略q∗关于c的变化趋势如图3所示,值函数ψ(u)如图4所示.

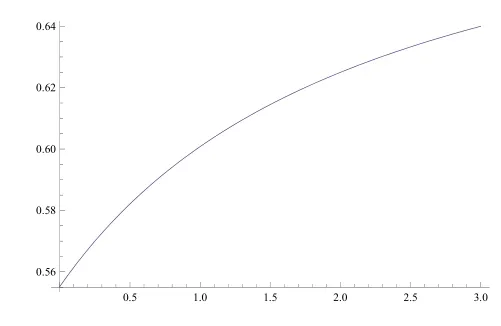
图1 相依参数λ对q∗的动态影响

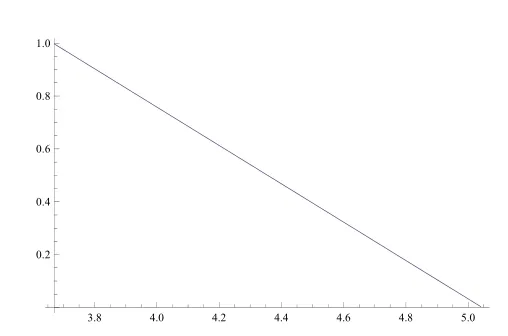
图3 收入率c对q∗的动态影响

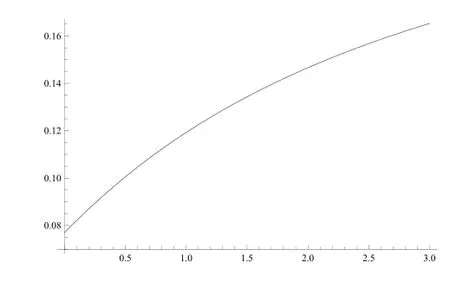
图2 相依参数λ对ψ(u)的动态影响

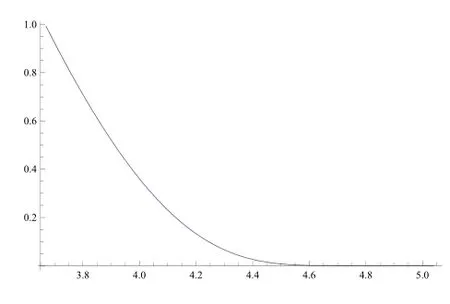
图4 收入率c对ψ(u)的动态影响

从图1和图2可以看出,最优自留风险水平关于相依参数λ单调递增,同时破产概率上升.实际上,由于直接保险采用期望值原则,未考虑相依风险部分,而再保险采用方差原则,包含了相依风险的再保险费,所以保险公司选择更多自留风险的策略是合理的,否则由于再保险更为昂贵,会导致更多的期望损失.注意,这与Bai et al.[13]均在期望值原则下所得结果有所不同,因为那里超额赔款再保险的最优自留风险限额是先减后增的.可见,采用不同形式的分保费原则,不仅最优再保险形式不同,对最优自留风险也会产生直接影响.

观察图3和图4发现,最优自留风险水平关于直接保险的保费收入率c直线下降,破产概率也迅速递减.这说明最小化破产概率的优化准则下,若混合采用期望值保费原则和方差分保费原则,最优再保险策略与保费收入率c有关,且非常敏感.Bai et al.[13]均采用期望值保费原则所得出的最优策略(定理4.1)也表明了二者的相关性.然而,在最大化期望指数效用的优化准则下,不论是对跳跃风险模型还是对扩散逼近模型,也不论直接保险费采取何种计算方式,最优策略都与c无关(详见Liang&Yuen[14]定理3.1和4.1及Yuen et al.[15]定理3.1和4.1).这直观说明了最小化破产概率这一优化标准的内在客观性.需要指出的一个特殊情形是,如果这里的直接保险也采用类似的方差原则且安全负载为η＜θ,则最优再保险策略退化为1−η/θ,与c无关.

§5 结论

本文采用相依多险种模型刻画保险公司的索赔风险过程,按照方差原则计算再保险费.通过扩散逼近,指出了比例再保险形式可最小化破产概率,并在不限定直接保险费计算方式的条件下,利用动态规划原理得到了最优再保险比例和最小破产概率的解析表达式.特别的,混合采用期望值保费原则和方差分保费原则,结合数值案例与期望值分保费原则比较,发现方差原则分保费下,再保险费包含相依风险部分,最优再保险形式为比例再保险,最优比例随相依强度的上升而增大;而期望值分保费原则下,再保险费不含相依风险部分,最优再保险形式为超额赔款再保险,最优限额随相依强度的上升而先减后增.可见,分保费计算方式对最优再保险形式和自留风险均产生直接影响.进一步,结合数值案例与最大化期望指数效用的最优策略比较,发现最小化破产概率的最优策略,不仅与安全负载、索赔分布、索赔计数过程都相关,还与直接保险的保费收入率c也有着非常敏感的关联性.这些可为保险公司优化再保险决策提供一些启示与参考.

[1] Schmidli H.Optimal proportional reinsurance policies in a dynamic setting[J].Scandinavian Actuarial Journal,2001,2001(1):55-68.

[2] Hipp C,Taksar M.Optimal non-proportional reinsurance control[J].Insurance:Mathematics and Economics,2010,47(2):246-254.

[3] Cao Yusong,Zeng Xianquan.Optimal proportional reinsurance and investment with minimum probability of ruin[J].Applied Mathematics and Computation,2012,218(9):5433-5438.

[4] 张茂军,南江霞,夏尊铨.再保险与有限时间破产概率[J].高校应用数学学报,2007,22(4):411-415.

[5] Kaluszka M.Mean-variance optimal reinsurance arrangements[J].Scandinavian Actuarial Journal,2004,2004(1):28-41.

[6] Cai Jun,Tan Kenseng,Weng Chengguo,et al.Optimal reinsurance under VaR and CTE risk measures[J].Insurance:Mathematics and Economics,2008,43(1):185-196.

[7] Chi Yichun.Optimal reinsurance under variance related premium principles[J].Insurance:Mathematics and Economics,2012,51(2):310-321.

[8] Bai Lihua,Guo Junyi.Optimal proportional reinsurance and investment with multiple risky assets and no-shorting constraint[J].Insurance:Mathematics and Economics,2008,42(3):968-975.

[9] 林祥,李艳方.跳-扩散风险模型的最优投资和再保险策略[J].应用数学学报,2013,36(5):791-802.

[10]Hald M,Schmidli H.On the maximization of the adjustment coefficient under proportional reinsurance[J].ASTIN Bulletin,2004,34(1):75-83.

[11]Liang Zhibin,Guo Junyi.Optimal proportional reinsurance and ruin probability[J].Stochastic Models,2007,23(2):333-350.

[12]Centeno M.Dependent risks and excess of loss reinsurance[J].Insurance:Mathematics and Economics,2005,37(2):229-238.

[13]Bai Lihua,Cai Jun,Zhou Ming.Optimal reinsurance policies for an insurer with a bivariate reserve risk process in a dynamic setting[J].Insurance:Mathematics and Economics,2013,53(3):664-670.

[14]Liang Zhibin,Yuen K C.Optimal dynamic reinsurance with dependent risks:variance premium principle[J].Scandinavian Actuarial Journal,2014,DOI:10.1080/03461238.2014.892899.

[15]Yuen K C,Liang Zhibin,Zhou Ming.Optimal proportional reinsurance with common shock dependence[J].Insurance:Mathematics and Economics,2015,64(1):1-13.

[16]Fleming W H,Soner H M.Controlled Markov processes and viscosity solutions[M].second ed.New York:Springer Science&Business Media,2006.

Optimal reinsurance of a dependent mulit-type risk model under variance reinsurance premium principle

ZHANG Jie-song1,2,XIAO Qing-xian1
(1.Business School,University of Shanghai for Science and Technology,Shanghai 200093,China;2.School of Management,Huaibei Normal University,Huaibei 235000,China)

In this paper,the optimal reinsurance strategy is considered to minimize the ruin probability of a risk model with multiple dependent classes of insurance under variance reinsurance premium principle.Through di ff usion approximation of the claim risk process and by applying the dynamic programming approach,explicit expressions of the optimal strategy and the value function are obtained.Moreover,by comparing to the results obtained under the expected value reinsurance premium principle,it is found that the optimal reinsurance form and the retention risk level are both di ff erent.By comparing to the results which maximize expected exponential utility,it is found that the optimal reinsurance proportion here depends not only on safety loading,but also on the claim distribution,the counting process and the premium rate of insurance c.Finally,combining with numerical example,dynamic impact of the dependence parameter is demonstrated and sensitive correlation between the optimal strategy and c is illustrated.

variance reinsurance premium;dependent multi-type risk model;optimal reinsurance;ruin probability

60G35;93E20

O211.6;F840

A

:1000-4424(2016)03-0253-09

2015-09-28

2016-04-17

国家自然科学基金(11171221);安徽省自然科学基金(1608085QG169);安徽省高校优秀青年人才支持计划重点项目(gxyqZD2016104)