非线性Black-Scholes模型下阶梯期权定价

孙玉东,师义民, 童 红

(1.贵州民族大学理学院,贵州贵阳550025;2.西北工业大学应用数学系,陕西西安710072)

非线性Black-Scholes模型下阶梯期权定价

孙玉东1,师义民2, 童 红1

(1.贵州民族大学理学院,贵州贵阳550025;2.西北工业大学应用数学系,陕西西安710072)

在非线性Black-Scholes模型下,研究了阶梯期权定价问题.首先利用多尺度方法,将阶梯期权适合的偏微分方程分解成一系列常系数抛物方程;其次通过计算这些常系数抛物型方程的解,给出了修正障碍期权的近似定价公式;最后利用Feymann-Kac公式分析了近似结论的误差估计.

阶梯期权;非线性Black-Scholes模型;Feymann-Kac公式;误差估计

§1 阶梯期权的偏微分方程模型

由于障碍期权的价格要比欧式期权还要低,所以近些年来障碍期权越来越受到消费者青睐,但它也存在不足:对于敲出障碍期权的持有者而言,当原生资产价格触及到障碍值时会导致期权立刻失效,他就失去了全部的投资.因此,人们考虑引进新的思路去修正障碍期权,这便产生了阶梯期权.

近些年来,有关阶梯期权解析定价公式方面的研究还未见文献,笔者只找到如下几处理论和数值方面的研究,文献[1-2]给出了阶梯期权所满足的偏微分方程模型,其中文献[1]还提供了研究阶梯期权的多种数值方法,例如特征线差分方法.戴清在文献[3]中利用前向打靶网格方法给出了阶梯期权的数值结论.基于分数步算法和两点中心隐式差分方法,罗俊和吴雄华采取初值的奇性消除技术,获得了阶梯期权的一个较高精度的差分格式,最后分析了容许延迟时间及障碍位置对期权价格的影响(文献[2,4]将阶梯期权称之为累积巴黎期权,本文统一采用文献[1]中的命名方法,称之为阶梯期权).

既然对于阶梯期权不能得到其精确解析定价公式,那么找到一个数学上一致性和严密的近似解也不失为一个很好的研究方向.基于此,本文在混合分数布朗运动驱动的非线性Black-Scholes模型下研究阶梯期权定价问题,其中原生资产价格St满足非线性随机微分方程

无风险资产价格Mt满足

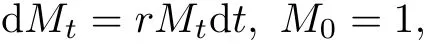
其中S0＞0为原生资产的初始价格,(a和b为非负常数),为分数布朗运动,wt为与之相互独立的标准布朗运动,常数r表示无风险资产的利率,µ(t,St)表示风险资产的期望收益率,σ0(t,St;ε)表示风险资产的波动率,ε(0 ＜ ε＜ 1)为摄动参数,µ(t,St)和σ0(t,St;ε)为时间t和股票价格St的一般函数.

下面以下降敲出期权为例刻画阶梯期权.当原生资产价格St下跌触及(或者越过)障碍值B时,下降敲出类型的阶梯期权的收益开始衰减,若是标准的障碍期权,立刻失效.假设衰减率为ρ,并用Ps.t(t,τ,S)表示下降敲出类型的看跌阶梯期权(Step Option)的价格,则该期权在到期日的损益就变为

其中τt表示在时间段[0,t]内原生资产价格在障碍值下方B(包)障碍值)停留时间的总和,即

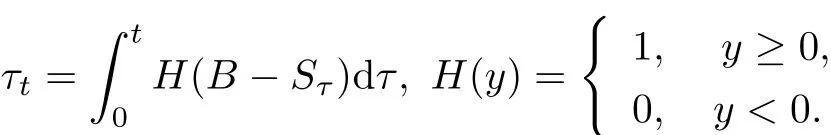
可以看出,当ρ=0时,阶梯期权转化为标准的欧式期权;当ρ→∞时,阶梯期权转化为下降敲出障碍期权.由文献[1]可知,下降敲出类型的看跌阶梯期权的价格Ps.t(t,τ,S)为如下形式的偏微分方程初值问题的解

在不至于引起混淆的情况下,用(eη−1)H(B−S)∂τPs.t代替,否则,作变换H(B−S)∂τPs.t,用τ′代替τ完成证明.因此,公式(12)可以被重新写为

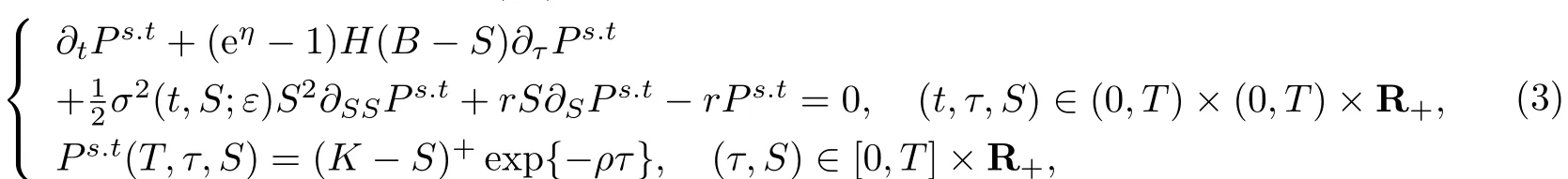
这里0＜η＜1.同理,若用Cs.t(t,τ,S)表示下降敲出类型的看涨阶梯期权的价格,则它等价于如下形式的偏微分方程初值问题

接下来,将采用多次多方法给出两种阶梯期权的定价公式,并采用Feymann-Kac公式给出结论的误差估计.本文提供的方法同样适合其他期权,例如欧式期权,亚式期权以及回望期权.

§2 多尺度方法

为方便叙述,首先定义如下的符号

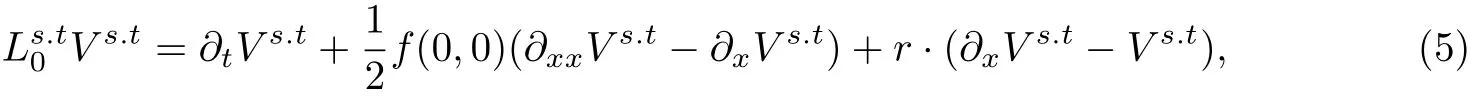
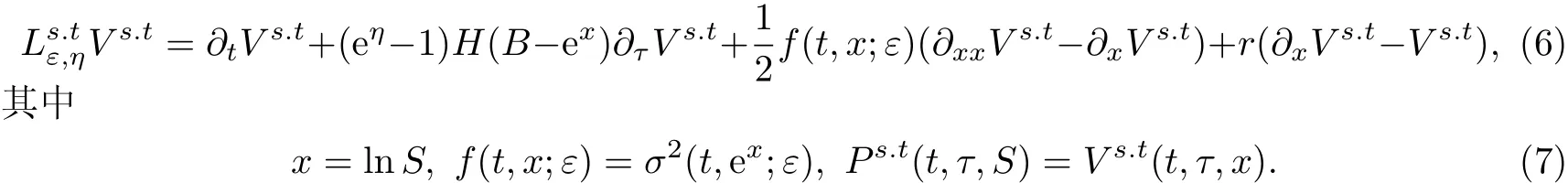
容易看出公式(7)提供了一个由Ps.t(t,τ,S)到Vs.t(t,τ,x)的变换,并且在该变换下偏微分方程问题(12)变为

假定当ε=0时f(t,x;ε)为与t和x 无关的常数,即f(t,x;0)=f0(0,0),并且f(t,x;ε)在ε=0附近展成如下形式的幂级数

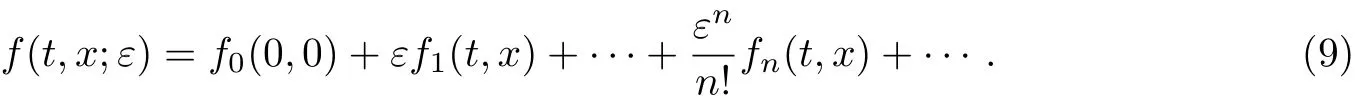
fn(t,x)表示f(t,x;ε)对ε的n 阶导数在ε=0处的值.由于f(t,x;ε)= σ2(t,ex;ε)＞ 0,所以这里假设f0(0,0)＞0.下面采用多尺度方法(双参数摄动展开方法)去处理偏微分方程初值问题(8).类推文献[5-6],为了得到偏微分方程初值问题(8)的解,将Vs.t(t,τ,x)在(ε,η)=(0,0)附近展开成幂级数

并将上述级数代入偏微分方程初值问题(8)的主方程,有

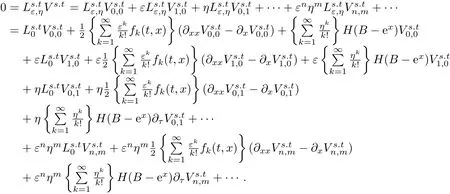
比较ε和η同次幂的系数,可以得到

由x和t的任意性,可令ε和η的相同次幂项的系数为零,从而

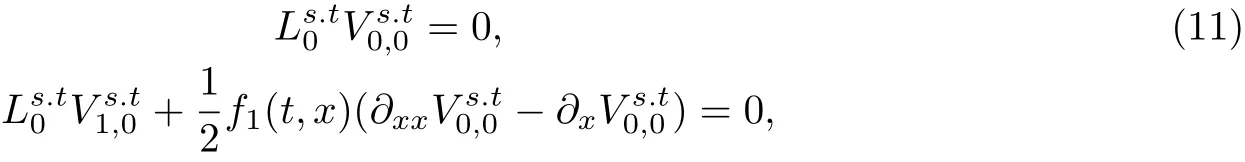
同时,根据公式(10)将偏微分方程初值问题(8)中初值条件进行分解

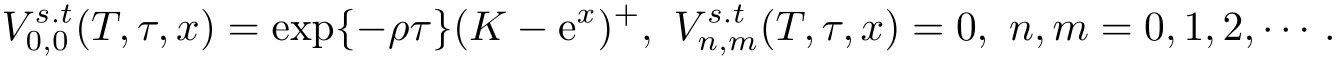
至此,抛物型方程(8)的求解问题转化为一系列常系数抛物方程初值问题,并且这些常系数抛物初值问题是可解的,其中为抛物方程初值问题

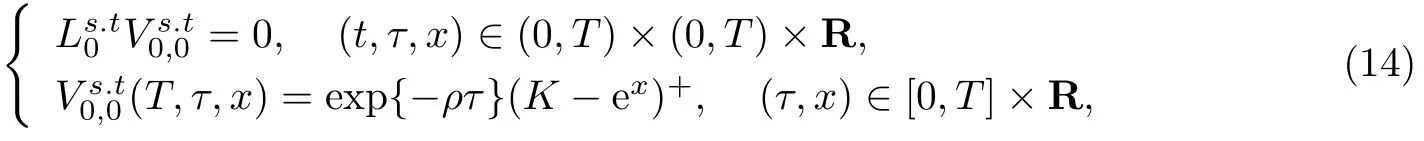
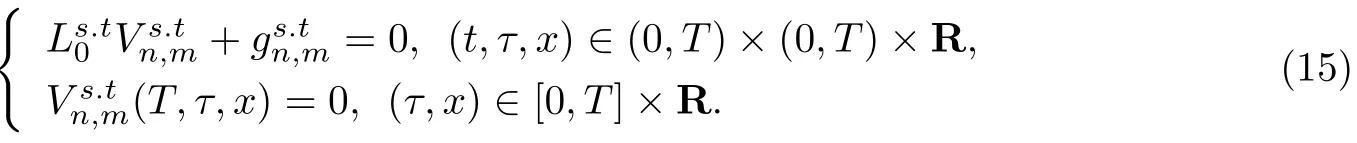
观察抛物初值问题(14)和(15)可以看出,主方程中不含变量,它只作为参量出现在初值条件中,所以在以下证明过程中将其视为常数.此外(13)中g不包含这样的项,这是§4能进行误差分析的关键.

§3期权定价公式

引理1若是常系数抛物方程初值问题(14)的解,则它可表示为

其中N(x)表示标准正态分布的概率累积函数,

引理2线性抛物方程(15)的解可表示为

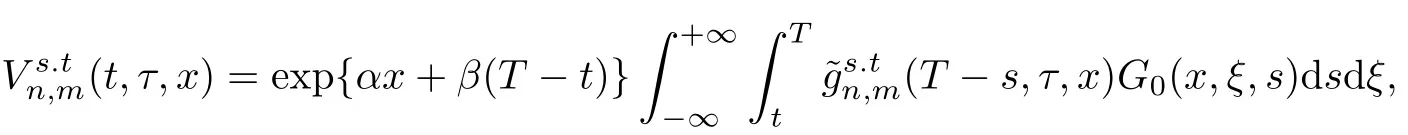
其中

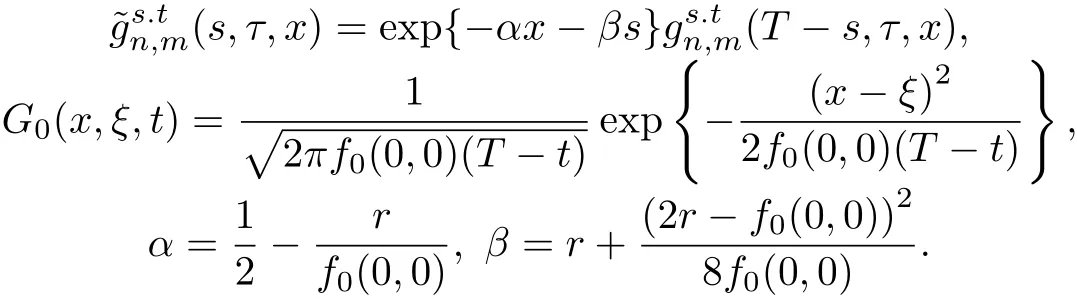
证注意到计算是已知的,因此将τ视为常数,并作变换

则抛物方程初值问题(15)可以转化为如下形式

对变换(16)进行逆变换可完成定理证明.

观察引理1,引理2以及公式(13),易得

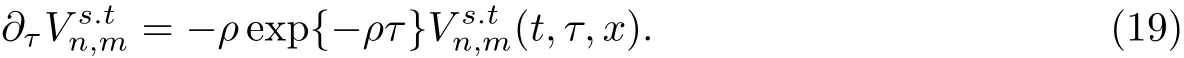
定理1假定Ps.t(t,S)表示下降敲出类型的看跌阶梯期权的价格,则它可以表示为

同理可证下降敲出类型的看涨阶梯期权定价公式,这里只给出结论.

定理2若Cs.t(t,τ,S)表示下降敲出类型的看涨阶梯期权的价格,则它可以表示为

x,α ,β,G0(x,ξ,t),d1和d2见定理1.

§4 误差估计

本节,将在如下假设下考虑近似结论的误差估计问题:假设fn(t,x)在[0,T]×R+上一致有界,即对任意的(t,x)∈[0,T]×R+以及任意正整数n,存在正常数M0,使得

并假定对任意的(t,x)∈[0,T]×R+有

引理3对任意的(t,τ,x)∈[0,T]×[0,T]×R,存在不依赖t,τ和x的正常数M1使得

证由引理1直接计算容易得到

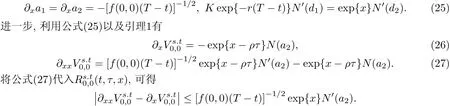
容易验证∀(t,τ,x)∈ [0,T]×[0,T]×R都有在[0,T]×R上有界,即存在正常数M3使得0＜exp{x}N′(a2)≤M3.取M1=M3(f0(0,0))−1/2,易得公式(25)中第一个不等式成立.

下面用Green函数证明公式(24)中第二个不等式成立.由文献[8]可知,抛物问题(14)的解存在格林函数G(x,y,τ),使得

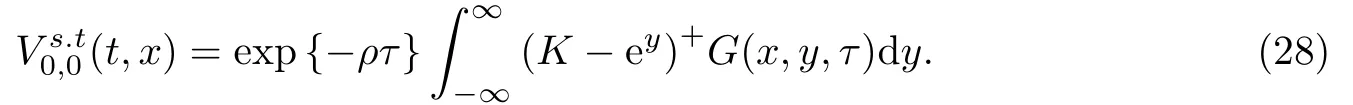
进一步,由文献[9]第4章第16节可知,存在正常数M4和M5,使得

将公式(29)代入公式(28)得到

因此公式(24)中第二个不等式也成立.

引理4当T足够小时,对任意的非负整数m和n(n2+m2＞0),存在不依赖x和t的非负常数M6和M7,使得

证明过程类似文献[10]之引理2.6,只需用引理3代替文献[10]中的引理2.5,这里不再赘述.

引理5对任意的(t,τ,x)∈[0,T]×[0,T]×R 有

因此利用文献[11]中定理13.11,可得

引理5和公式(19)表明:Vs.t(t,τ,x)对变量τ的偏导数与Vs.t(t,τ,x)成线性关系,这意味着是抛物算子,即

因此本文可以根据抛物方程的Feyman-Kac公式研究Vs.t(t,τ,x)的近似解的误差估计问题.

根据上面的辅助引理,下面给出本节的两个主要结论.

定理3当T足够小时,存在不依赖x,t和τ的正常数M,使得

利用公式(19)和公式(30),上述偏微分方程初值问题可以被重新写为

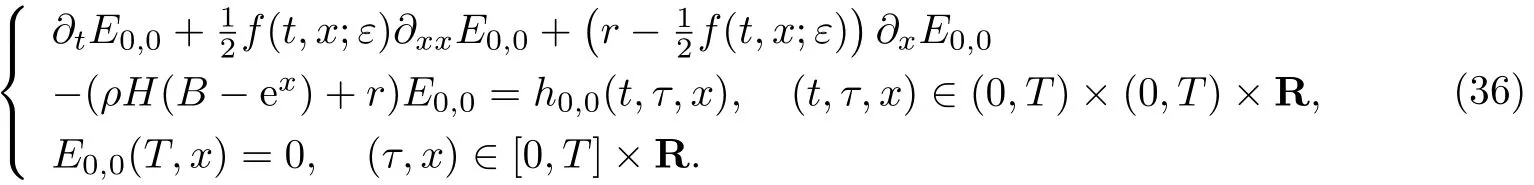
一方面,由引理3可得

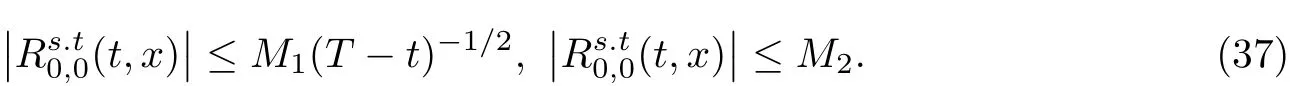
又由公式(21),对任意的(t,x)∈[0,T]×R+

注意到0＜η＜1,由中值定理可知,存在θ∈(0,η)使得

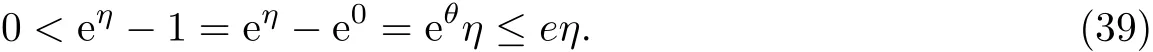
因此将公式(38)和(39)代入公式(35),对任意的(t,x)∈[0,T]×R+,h0,0(t,x)满足

另一方面,由Feymann-Kac公式可知[12],抛物初值问题(36)的解可以表示为如下形式的条件概率问题

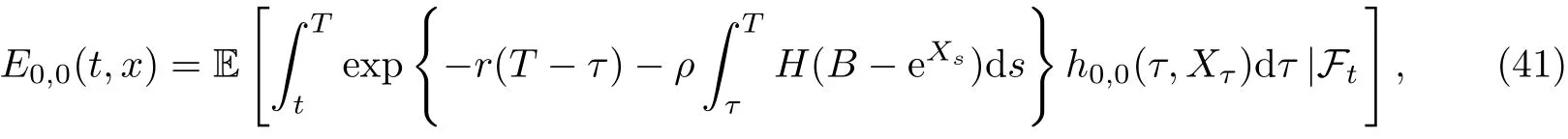
其中Xt为随机微分方程

的解,t≤ s≤ T,Xt=x.因为公式(23)已经说明f(t,x;ε)和关于变量x满足线性增长条件,所以由文献[12]定理4.1,随机微分方程(42)存在解E0,0(t,x).最后,将公式(40)代入公式(41)可得E (t,x)的一个估计

定理4假定T足够小并且存在正整数ω0使得在[0,T]×[0,T]×R+上一致收敛到Ps.t(t,τ,S),即对任意的正整数n和m,存在不依赖n,m,x和t的正常数M使得

这里M 依赖ω0.

证类似定理3,这里只需证明

其中

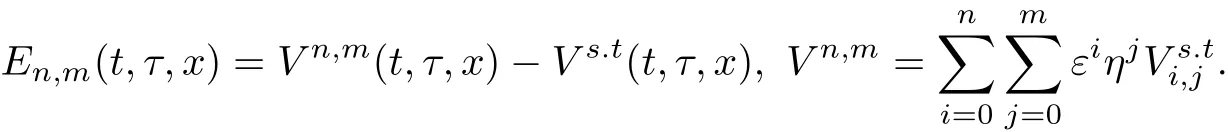
显然En(t,τ,x)满足如下的初值条件

又因为

所以有

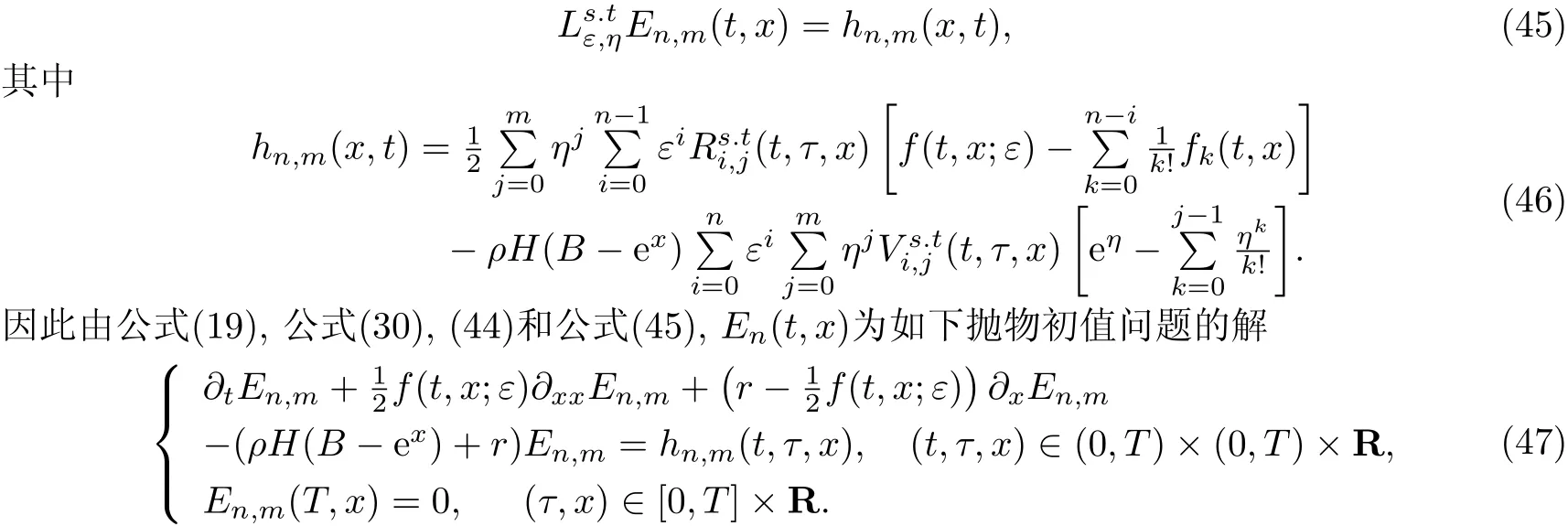
接下来,将证明分为两步:

第一步首先利用公式(21),可得对任意的(t,τ,x)∈[0,T]×[0,T]×R有

第二步利用Feynman-Kac公式可知[12],抛物初值问题(47)的解可表示为如下形式的条件概率问题

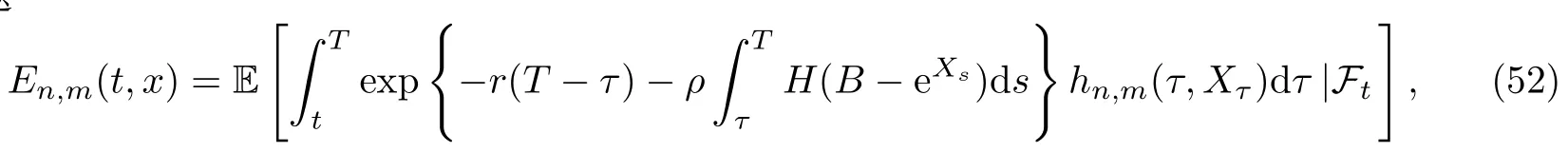
其中Xτ满足随机微分方程(42).将公式(51)和公式(43)代入公式(52)可知,En(t,x)满足估计式

因此取M 为上式右端,可完成定理证明.

§5数值模拟

本节利用数值模拟的方法,对所提出的误差估计结果进行考察.根据Black-Scholes公式,当波动率为常数σ时,欧式看涨期权是有精确解的,这里假定波动率σ=0.5,并人为设定小参数ε使得σ=ε+σ0.接下来,依据定理1从σ0开始模拟阶梯期权的价格,然后与σ=0.5时的期权精确结果进行比对.这里取无风险利率r=0.05,交割价格K=100,则Pi的Matlab结果如下： 上述表格中精确值是采用蒙特卡洛方法模拟5000次所得结果,模拟过程中假设η=0.5,m=5,仅考察ε对误差估计效果的影响.此外上述模拟中Pn表示

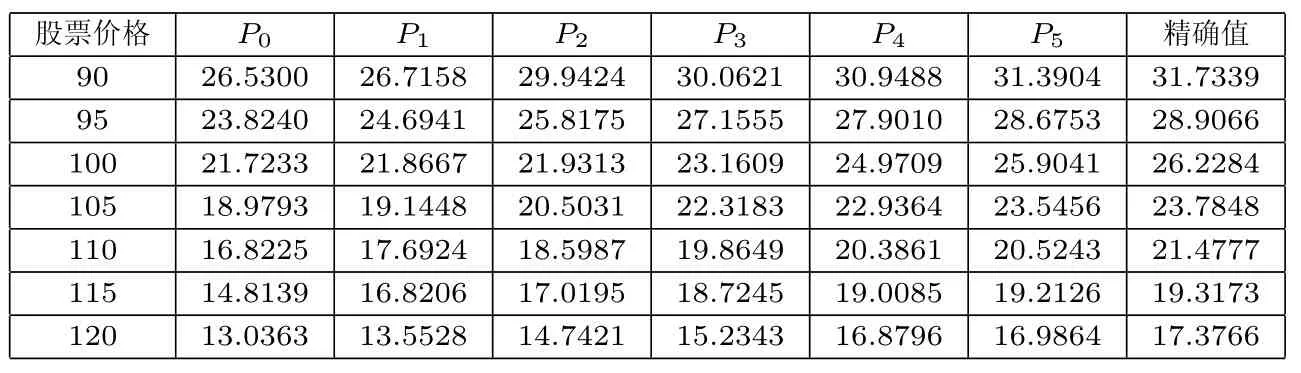
表 1 阶梯看跌期权(ε=0.1)

表 2 阶梯看跌期权(ε=0.2)

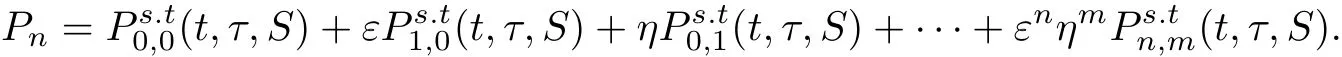
观察表2.1可以看出随着阶数n和m的增大,近似解逐步逼近期权价格的精确解.同时对比表格表2.1(a)和表2.1(b)也可以看出当ε=0.1时,P3已经比较接近真是价格,当ε=0.2时,需要计算到P5才有比较好的近似结果,这说明ε越小逼近的速度越快,这恰与定理1所得误差估计结论相符.

参考文献:

[1] 姜礼尚.期权定价的数学模型和方法(第二版)[M].北京:高等教育出版社,2008.

[2] 郭冬梅,宋斌,汪寿阳.倒向随机微分方程与巴黎期权的非线性定价[J].中国科学A辑,2013,43(1):91-103.

[3] 戴清.阶梯期权价格的计算方法[J].经济数学,2003,20(2):92-94.

[4] 罗俊,吴雄华.巴黎期权定价问题的数值方法[J].数值计算与计算机应用,2004,25(2):81-89.

[5] 瓦西里耶娃,布图索夫.奇异摄动方程解的渐近展开[M].北京:高等教育出版社,2008.

[6] 郑连存,张欣欣.非线性偏微分方程近代分析方法[M].北京：科学出版社,2011.

[7] 孙玉东,师义民.修正的Black-Scholes模型下的欧式期权定价[J].高校应用数学学报,2012,27(1):23-32.

[8] Chen Yazhe.The second order parabolic partial di ff erential equations[M].Beijing:Peking University Press,2002.

[9] Ladyzenskaja O A,Solonikov V A,Uralceva N N.Linear and Quasilinear Equations of Parabolic Type[M].New York:American Mathematical Society,1964.

[10] 孙玉东.非线性Black-Scholes期权定价模型研究[D].西北工业大学,2014.

[11] Yin Hongming.A uniqueness theorem for a class of non-classical parabolic equations[J].Applicable Analysis,1989,34(2):67-78.

[12] 金志明.随机分析基础[M].北京:国防工业出版社,2001.

The pricing of step options under the nonlinear Black-Scholes model

SUN Yu-dong1,SHI Yi-min2,TONG Hong1,
(1.School of Science,Guizhou Minzu University,Guiyang 550025,China;2.Department of Applied Mathematics,Northwestern Polytechnical University,Xi’an 710072,China)

In this paper,the pricing problems of geometric average Asian options are studied under the nonlinear Black-Scholes model.Firstly,the partial di ff erential equations for the Asian options are transformed into a series of parabolic equations with constant coefficients by the perturbation method of single-parameter.Secondly,the approximate pricing formulae of the geometric average Asian options are given by solving those parabolic equations with constant coefficients.Finally,the error estimates of the approximate solutions are given by using Green function.

geometric average Asian options;nonlinear Black-Scholes model;Green Function;error estimates

60H10;90A06

O211.6;F830.9

A

:1000-4424(2016)03-0262-11

2015-09-26

2016-07-22

国家自然科学基金(71401134;71571144);贵州省科学技术基金(黔科合J字[2015]2076号);贵州民族大学引进人才科研基金(15XRY005);贵州省研究生卓越人才计划(ZYRC字[2014]008)