随机环境中马氏链状态的各种常返性与暂留性

费时龙

(宿州学院数学与统计学院,安徽宿州234000)

随机环境中马氏链状态的各种常返性与暂留性

费时龙

(宿州学院数学与统计学院,安徽宿州234000)

考虑到随机环境中马氏链的状态在受到环境因素各种条件的影响下,引入了随机环境中马氏链状态的各种常返性与暂留性概念,讨论了这些常返性与暂留性的相互关系,从而说明随机环境中马氏链状态的常返性与暂留性和经典马氏链状态的常返性与暂留性有着显著的区别.

随机环境;常返;强常返;暂留

§1 引 言

随机环境中的马氏链(以下简称MCRE)是随机过程的重要分支之一,有着丰富的应用背景.特别是两种特殊的随机环境中的马氏链-随机环境中的随机游动[1-4]与随机环境中的分支过程[5-6]已成为近年来的重要研究热点.它们在很多领域(如:生物学,保险学,神经网络,股市预测,物理学等)中有着广阔的应用背景.随着这两种特殊的随机环境中马氏链研究的不断深入和完善,Nawrotzi[7]和Cogburn[8-10]在20世纪80年代首先引入了随机环境中马氏链的一般理论,并借鉴Doeblin关于马氏链状态的一般分类方法将随机环境中的马氏链状态定义成正则本质,非正则本质,非本质三种情形,并深入研究了非正则本质状态不存在的充分条件.常返与暂留是马氏链中的最重要的概念,经典马氏链状态的常返性与暂留性研究已取得完善的结果,有很多常返性与暂留性的等价描述.然而,由于随机环境中马氏链的转移概率矩阵会受到随机环境因素的干扰,在定义状态时必须考虑环境的影响,其状态的常返性与暂留性与经典马氏链状态的常返性与暂留性有着显著的区别.肖争艳和胡迪鹤[11]引入了随机环境中马氏链状态的强常返,弱常返等概念,并讨论了强常返与弱常返的相互关系.李应求[12-14]引入了MCRE的几种暂留性概念,讨论了几种暂留性关系及判别准则,引入了π不可约的条件,并在该条件下获得了随机环境中马氏链状态只存在弱常返与强暂留的情形.费时龙[15]在环境是平稳遍历或强混合的条件下得到类似的结果.近些年来,MCRE的极限理论[16-17]受到人们的广泛关注,关于MCRE的一般介绍可参考文献[18].本文主要是在前人的研究基础上引入了随机环境中马氏链的几种新的常返性与暂留性,主要考虑随机环境中马氏链状态的常返性与暂留性在受到环境一致性影响的条件下,引入了最大常返,最小暂留,强一致暂留,弱一致暂留等概念,结合前人所引入的强常返,弱暂留等概念讨论了状态的各种常返性与暂留性的相互关系.在假定环境是平稳遍历的条件下得到了状态最大常返与弱暂留是对立的,弱常返与最小暂留是对立的结论,获得了状态弱常返与强常返的等价条件.

§2 MCRE模型和基本记号

本文中所用的一些记号和术语可参看文献[14].设(X,A)(Θ,B)为两个可测空间,其中X为至多可数集,A为X的离散σ-代数,{P(θ),θ∈Θ}是(X,A)上的转移函数族,且假定任意的x,y ∈ X,P(·;x,y)是关于B可测的.···,−1,0,1,···}分别是取值于X和Θ的两个随机序列.可以定义一个随机环境中的马氏链为:

定义2.1[7]若对任意的A∈A,n∈N,有

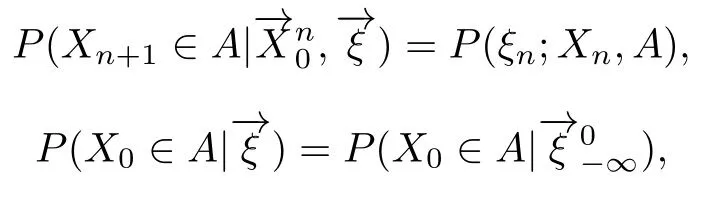
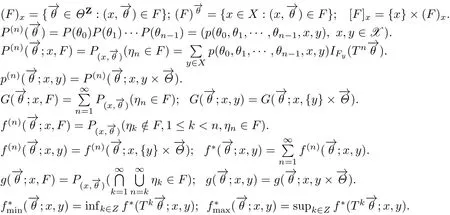
§3 状态的各种常返性和暂留性

本节将引入MCRE状态的各种常返性与暂留性概念,并讨论了他们的相互关系.记

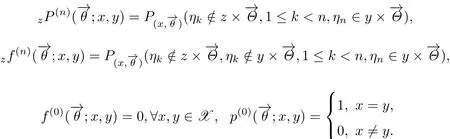
利用ηn的马氏性及首次前击中时和后击中时的分解,显然有下列结论成立:

引理3.1设z/=y,x/=y,则对任意的n≥0,有

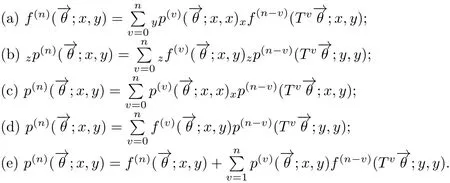
特别的,当x=y时,有下列结论成立:

推论3.1对任意的n≥1,有

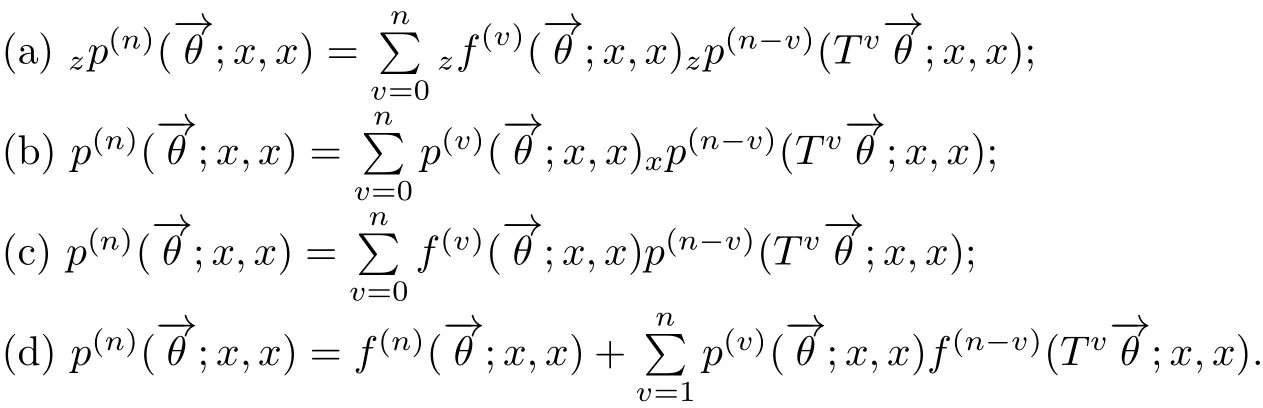
文献[9]利用经典马氏链中状态的平均返回次数无穷的条件及无穷次返回概率为1的条件引入了下列MCRE状态的弱常返,强常返等概念.

定义3.1[9]称状态x是弱常返的,若称状态x是强常返的,若

命题3.1[9](i) 状态x是强常返的当且仅当

(ii)若状态x是强常返的,则状态x是弱常返的.

定义3.2称状态x是强暂留的, 若称状态x是弱暂留的,若π称状态x是强一致暂留的,若存在常数C:0 ＜ C ＜ 1,使得π;称状态x是弱一致暂留的, 若存在常数M ＞ 0,使得

定理3.1若状态x是强一致暂留的,则状态x是弱一致暂留的.

证由推论3.1的(d)知

从而

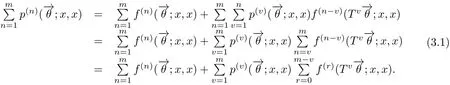
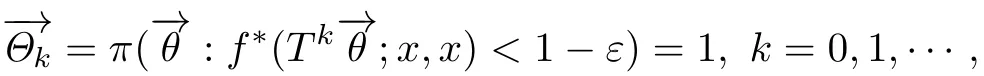
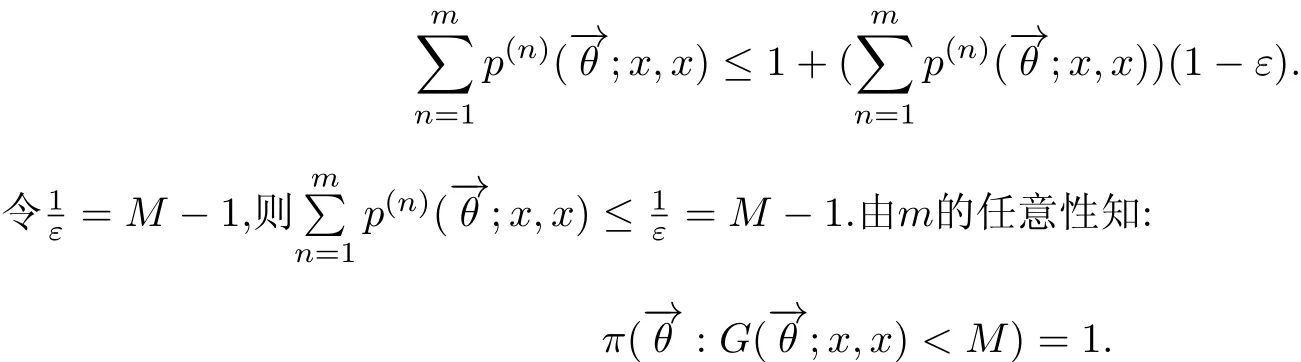
即状态x是弱一致暂留的.

定理3.2若状态x是弱一致暂留的,且存在常数C＜1,使得对任意的k≥1,有

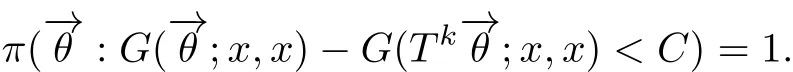
则状态x是强一致暂留的.

证设状态x是弱一致暂留的,则存在常数M ＞0,使得π(−→θ:G(−→θ;x,x)＜M)=1.令

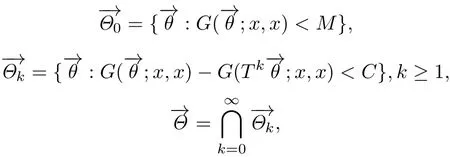
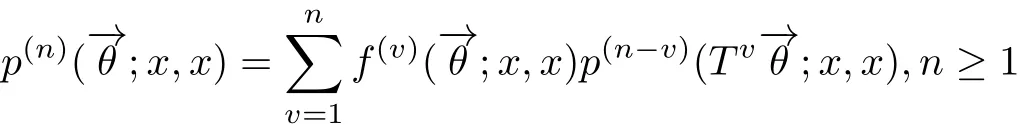
得

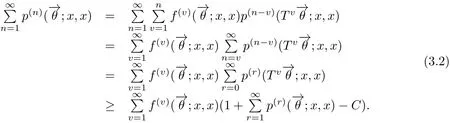
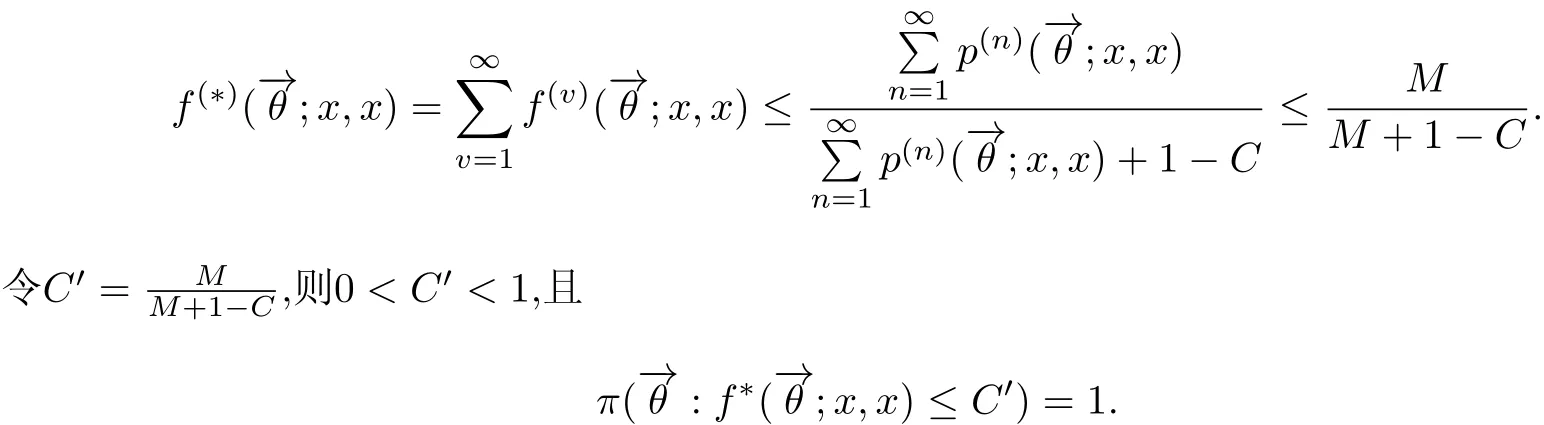
故状态x是强一致暂留的.

下面引入最小常返,最大常返,最小暂留,最大暂留,最小一致暂留,最大一致暂留等概念,并讨论它们的相互关系.

定义3.3称状态x是最大常返的,若称状态x是最大暂留的,若称状态x是最大一致暂留的,若存在常数C:0＜C＜1,使得;称状态x是最小常返的,若称状态x是最小暂留的,若π称状态x是最小一致暂留的,若存在常数C:0＜C＜1,使得π

注状态x是最小常返的直观含义为：对几乎处处的环境,经过任意步环境的推移后,从状态x出发在有限步内必然能回到状态x；最大常返的直观含义为：对几乎处处的环境,总存在k步环境的推移后,从状态x出发在有限步内必然能回到状态x；最大暂留的直观含义为：对几乎处处的环境,对任意步环境的推移,从状态x出发经过有限步后必然离开状态x；最小暂留的直观含义为：对几乎处处的环境,总存在k步环境的推移后,从状态x出发经过有限步后必然离开状态x；最大一致暂留的直观含义为：在最大暂留的条件下,这里对所有的环境能被一个固定的常数所控制；最小一致暂留的直观含义为：在最小暂留的条件下,这里对所有的环境能被一个固定的常数所控制.

定理3.3若状态x是弱常返的,则状态x是最大常返的.

证设状态x是弱常返的,.对任意的由推论3.1的(d)知

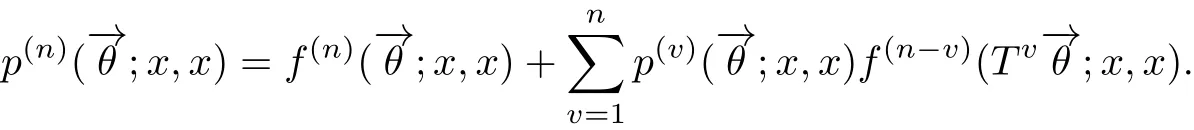
从而由定理3.1证明中的(3.1)式知

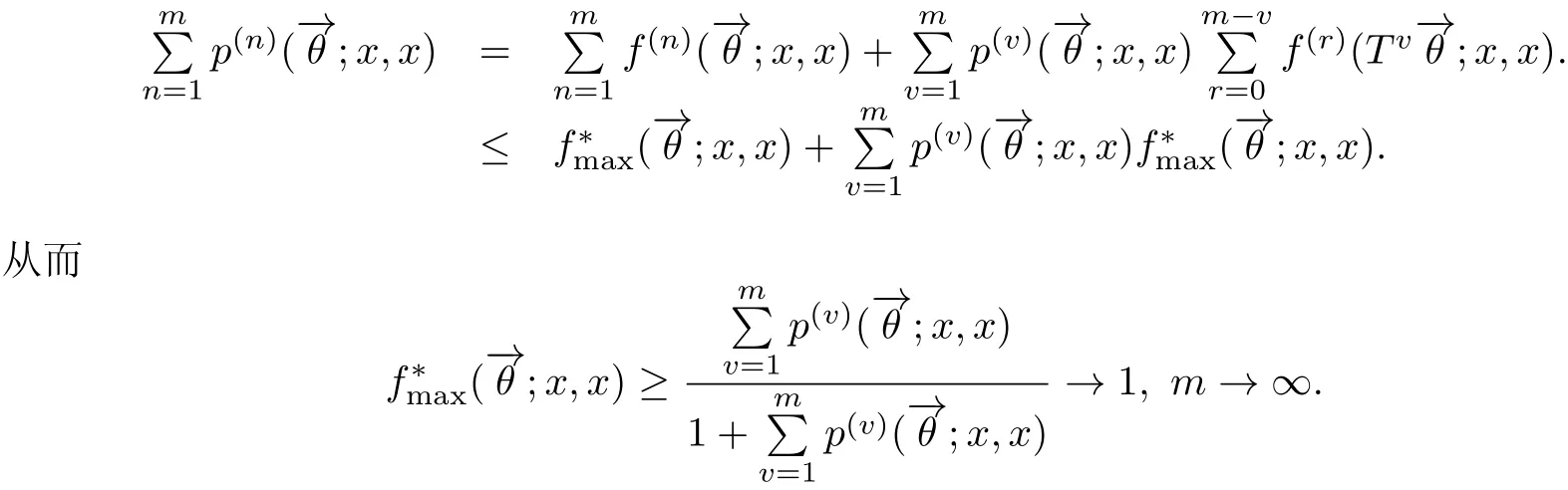
定理3.4(1)若状态x是弱暂留的,则状态x是最小暂留的.

(2)若状态x是一致弱暂留的,则状态x是最小一致暂留的.

证由推论3.1的(d)知

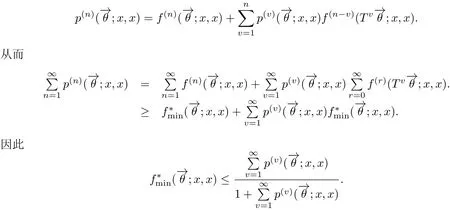
从而由定理的条件及定义3.3知(1),(2)成立.

定理3.5设π关于T是平稳遍历的,则

(1)任意状态x是为最大常返的或弱暂留的;

(2)任意状态x是为弱常返的或最小暂留的.

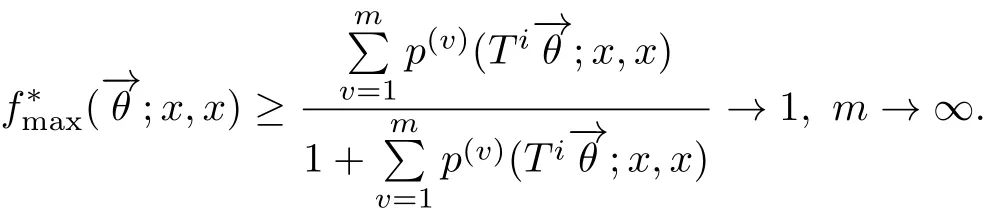
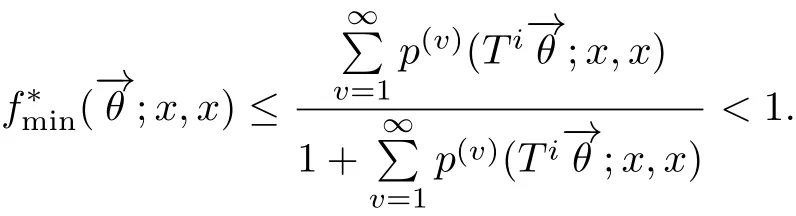
定理3.6若对几乎必然的存在正数使得对任意的k和m,均有

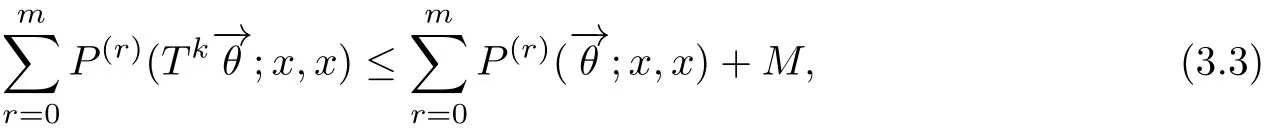
则状态x是强常返的当且仅当状态x是弱常返的.

证充分性由命题3.1的(ii)得到,下证必要性.设状态x是弱常返的,令

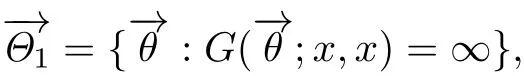
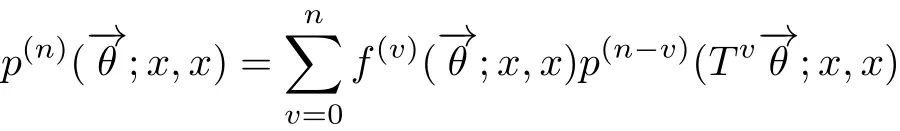
及条件(3.3)得

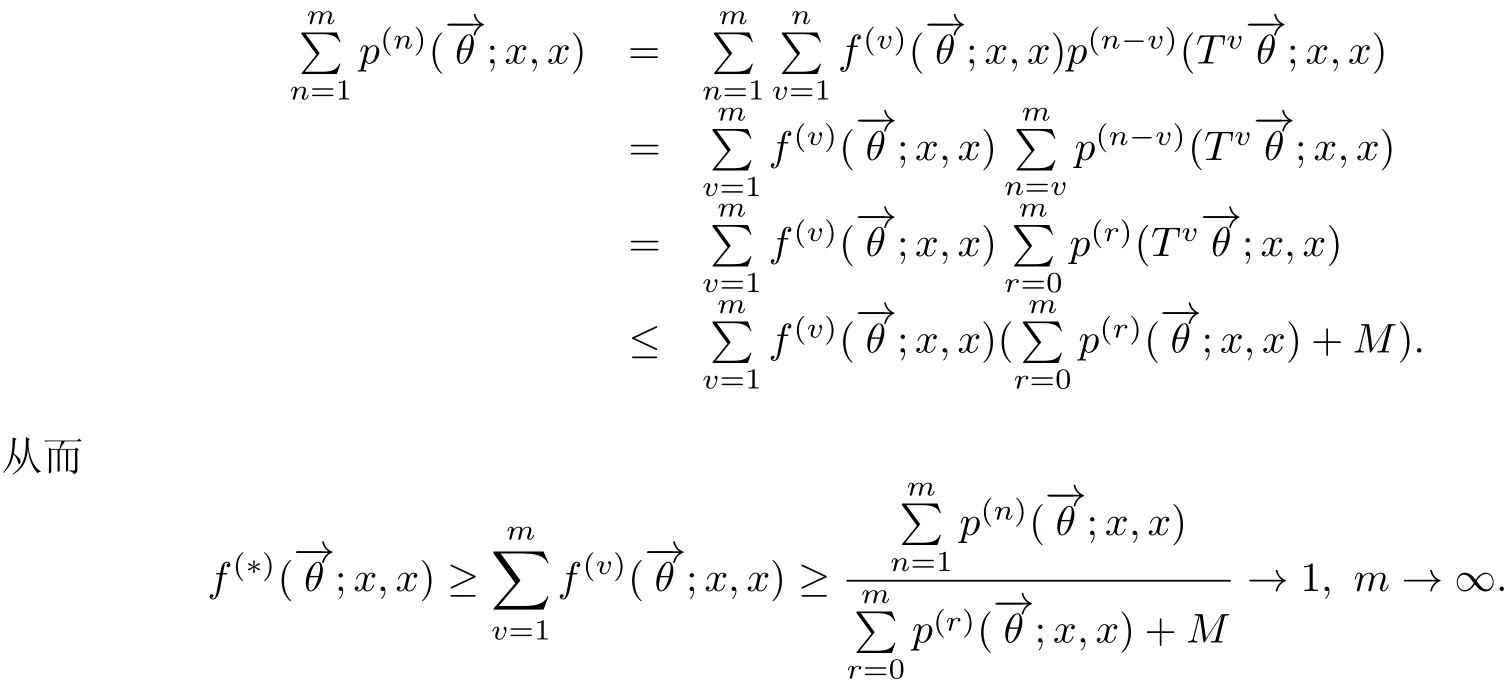
[1] Solomn F.Random walks in a random environment[J].Ann Probab,1975,3(1):1-31.

[2] Kozlov M V.On the asymptotic behavior of the probability of non-extinction for critical branching processes in a random environment[J].Theory Prob Appl,1976,21(4):742-751.

[3] Alili S.Persistent random walks in stationary environment[J].J Statist Phys,1999,94(3):469-494.

[4] Hong Wenming.Renewal theorem for(L,1)-random walk in random environment[J].Acta Math Sci,2013,33B(6):1736-1748.

[5] Smith W L,Wilkinson W E.On branching processes in random environments[J].Ann Math Statist,1969,40(3):814-827.

[6] 李应求,胡杨利,张影.随机环境中两性分枝过程的极限性质[J].中国科学A辑,2015,45(5):611-622.

[7] Nawrotzki K.Finite Markov chains in stationary random environments[J].Ann Probab,1982,10(4):1041-1046.

[8] Cogburn R.Markov Chains in random environments[J].Ann Probab,1980,8(3):908-916.

[9] Cogburn R.The ergodic theory of Markov chains in random environments[J].Z Wahrsch Verw Gebiete,1984,66(2):109-128.

[10]Cogburn R.On direct convergence and periodicity for transition probabilities of Markov chains in random environments[J].Ann Probab,1990,18(2):642-654.

[11]肖争艳,胡迪鹤.绕积马氏链的状态分类[J].数学物理学报,2003,23A(3):306-313.

[12]李应求.双无限环境中马氏链的常返性与不变侧度[J].中国科学A辑,2001,31(8):702-707.

[13]李应求.双无限随机环境中的常返马氏链[J].数学学报,2007,50(5):1099-1100.

[14]李应求.双无限随机环境中马氏链的暂留性[J].数学物理学报,2007,27(2):269-276.

[15]费时龙,任敏.随机环境中马氏链状态的常返性与暂留性[J].高校应用数学报,2011,26(2):187-194.

[16]万成高.随机环境中马氏链函数加权和的极限定理[J].数学物理学报,2015,35A(1):163-171.

[17]宋明珠,吴永锋.马氏双链函数的强大数定律及其应用[J].数学杂志,2015,35(2):368-374.

[18]胡迪鹤.随机环境中的马尔可夫过程[M].北京:高等教育出版社,2011.

Several recurrence and transience of states for Markov chains in random environments

FEI Shi-long
(School of Mathematics and Statistics,Suzhou University,Suzhou 234000,China)

Several concepts of recurrence and transience of states for Markov Chains in random environments are introduced under the in fl uence of various environmental factors,and their connections and properties are discussed.These conclusions present that the recurrence and transience of states for Markov Chains in random environments and the recurrence and transience of states for classical Markov chains have obvious di ff erences.

random environments;recurrence;transience

60J10;60J15

O211.62

A

:1000-4424(2016)03-0273-08

2015-06-10

2016-04-24

安徽省高等学校省级自然科学基金(KJ2016A770);安徽省高校优秀青年人才支持计划重点项目(gxyqZD2016340);安徽省教育厅人文社科研究重点项目(SK2016A1006)